节理岩质边坡稳定性概率分析

张宜杰,任光明,常文娟,董 斌,唐 杨

(1．地质灾害防治与地质环境保护国家重点实验室(成都理工大学)，成都 610059；2.中国电建集团 西北勘测设计研究院有限公司，西安 710065；3.国网四川省电力公司，成都 610041)

岩体具有一定的结构特征，其基本组成是结构面和由结构面所围限的岩块[1]。对于岩质边坡来说，其稳定性不仅与坡高、坡角、坡型以及岩体类型有关，而且与岩体中的结构面及其在空间的分布和组合状况相关。在传统的岩质边坡稳定性分析中，赤平投影法一般用于定性判断，无法考虑到结构面的迹长、间距、延续性等[2]；而极限平衡法未考虑岩土体变形对边坡稳定性的影响，不能求解边坡内各点的应力-应变状态以及位移分析[3-4]，因此均具有一定的局限性。20世纪60年代以来，随着计算机科学、数值分析法的发展，众多学者采用离散元、DDA等非连续变形方法分析节理岩体[5-9]，这些方法能合理描述岩体不连续力学行为，在节理岩体的模拟中具有较大的优越性。然而，这些方法还存在一些尚待改进的地方：离散元将边坡概化成离散刚性集合体，适用于分析贯通性结构面岩体，不能较好地反映实际岩体结构面的随机性和不连续性；在建模时需要知道每个结构面的力学性质及确切位置，当裂隙数量较多时，建模过程较困难并且计算分析耗时、收敛性差。

节理网络有限元法(Jointed finite element method，简称“JFEM”)则能很好地弥补这些不足。该方法将岩体定义为由岩块和节理组成的二元结构，在野外调查的基础上，利用Monte-Carto法生成节理网络模型，能够较好地反映实际岩体结构面非贯通、随机发育的特征；在此基础上进行有限元强度折减计算，不仅可以得到边坡的应力场、位移场以及塑性区分布，还可以得到边坡的稳定性系数以及分析边坡变形破坏趋势。一些学者也对此方法进行了研究，并取得一定的成果。R.E.Hammah等[10-11]应用有限元节理网络研究了节理边坡破坏的机理以及不同尺度对边坡稳定性的影响；Özgür Satc等[12]将有限元节理网络应用于土耳其某公路隧道入口围岩的稳定性评价中；宋彦辉等[13]认为节理网络有限元能够作为倾倒变形边坡稳定性评价的一种合理、可靠的分析途径；王宇等[14]基于Jaeger单结构面理论，运用有限元节理网络计算裂隙岩体的抗压强度，验证了有限元节理网络的可靠性；崔臻等[15]利用JFEM数值模拟法研究了不同结构面的几何参数对柱状节理岩体等效变形模量的影响。因此，有限元节理网络具有广阔的应用前景。

本文以中国西部某水电站左岸坝肩边坡为例，在现场调查的基础上，建立有限元节理网络模型，同时结合Rosenbluth点估计法充分考虑岩体强度参数(内摩擦角和黏聚力)的变异性[16]，计算了该边坡的稳定性系数，并结合现场实际情况进行分析。研究成果对该边坡的防治工程设计具有一定的指导意义，同时也为该类边坡的稳定性评价提供了较好的途径。

1 基本原理及模拟步骤

1.1 Baecher节理网络模型

本次模拟采用Baecher模型，根据野外调查获得的统计参数，利用Monte-Carlo法生成所需的裂隙网络。这种模型较为方便，能够快速模拟一系列复杂的非贯通、随机节理。在Baecher模型中，可以通过2种方法定义节理的产状：一种是Fisher概率分布函数法；另一种是指定节理的倾向和倾角。W.S.Dershowitz等[17]、M.C.Cacas等[18]认为Fisher分布具有相对较佳的拟合。Fisher分布又称球状正态分布，在空间上，裂隙面的倾角用其法线的方向表示，而一组裂隙面的法向量将围绕其代表法线和向量呈现Fisher概率函数分布，即

(1)

式中：f(θ)为概率密度函数；θ为均值向量的角标准偏差；K为Fisher常数或散度因子，用来表征结构面产状的离散程度，K值越小，表明结构面产状越离散。

1.2 点估计法原理

点估计法是基于E.Rosenbluth[19]提出的一种统计矩方法，其目的是能够结合概率输入变量和评估输出变量的分布。点估计法的原理是计算各个估计点的解，并将它们与适当的权重相结合，从而得到输出变量的近似分布。

对于一般的边坡稳定性问题，定义其状态函数为[20]

Z=F(x1,x2,…,xn)

(2)

式中:x1,x2,…,xn分别为容重、泊松比、黏聚力、内摩擦角等随机变量；Z为边坡稳定性系数，它们大部分服从正态分布或对数正态分布。已知n个随机变量(x1,x2,…,xn)的平均值μxi和标准差σxi，在随机变量xi(i=1,2,…,n)的分布函数未知的情况下，在区间(xmin,xmax)上分别对称地选择2个取值点，通常取均值μxi的一个正负标准差σxi，即[21]

(3)

对于n个随机变量，有2n个取值点，可得到2n个稳定性系数，即可求得稳定性系数Z的平均值μz和标准差σz。如果每个随机变量是彼此独立的，并且各个组合出现的概率一样，则Z的均值估计为[21]

(4)

标准差的点估计为[21]

(5)

假设随机变量服从正态分布，则可靠性指标β可以表示为[21]

β=(μz-1)/σz

(6)

破坏概率为[21]

Pf=1-φ(β)

(7)

1.3 模拟的步骤

a.现场调查及结构面采样。在现场调查过程中应查明坝址区的工程地质条件、边坡岩体的风化卸荷特征及变形特征，同时对结构面进行系统采样，利用测线法或测窗法测量、统计随机结构面的产状、迹长、间距等特征参数。

b.结构面概率模型的建立。首先对坝址区的几组优势结构面具有宏观认识，在此基础上，绘制节理极点等密度图，对结构面进行分组，统计每组结构面的特征参数的分布形式，并建立相应的概率模型[22]。

c.节理网络模拟。根据边坡岩体结构面的特点选择合适的模型，并且根据每组结构面特征参数的概率分布特征值，采用Monte-Carto法，生成符合一定概率分布的随机数列来模拟结构面网络，沿指定方向剖切得到边坡的二维结构面网络图。

d.结合Rosenbluth点估计法对节理网络模型进行计算，结合现场实际情况对结果进行分析。

2 边坡的工程地质条件

2.1 边坡的基本地质条件

某水电站位于黄河干流上，坝顶长度151 m、海拔高度1 751 m，电站正常蓄水位海拔高度 1 748 m。工程区属高原半干旱高寒性气候区，常年干旱少雨，地下水不丰富。坝址区河谷狭窄、岸坡高陡，沿线花岗岩高边坡众多，两岸平均坡度50°～70°。左岸边坡受冲沟影响，岸坡整体凹向岸内，中间微凸，凸形体平面上呈“倒梨形”，两侧形成小冲沟。自然坡角相差悬殊，原海拔高度 1 750～1 780 m为缓坡地段，坡度20°～34°，施工期采用混凝土贴坡支护。海拔高度 1 780 m以上陡坡地段的坡度为73°～80°，局部近直立，卸荷拉裂严重，有掉块现象。因此有必要分析评价该边坡的稳定性及失稳模式，为综合防治方案提供依据。

2.2 边坡的岩体结构特征

3 节理网络有限元模拟

3.1 节理地质参数概率模型的建立

现场采用测线法进行节理的几何参数统计，共获得1 065条节理的现场测量数据，节理极点等密度图如图1所示。利用聚类分析法将结构面分为J1、J2、J3三个优势组，平均优势产状分别为17.9°∠75°、152.8°∠68°、305.5°∠36°。对各组优势结构面的间距、迹长进行统计分析，拟合概率密度分布函数，结果显示各组优势结构面的迹长、间距均近似服从负指数分布。3组优势结构面几何特征参数如表1所示。

图1 节理极点等密度图Fig.1 Contour map for stereographic projection of joints

3.2 计算模型及参数的确定

根据表1中的值，运用Monte-Carlo法，采用phase2有限元软件，生成有限元节理网络模型(图2)。以自重应力场作为边坡初始应力，不考虑构造应力等因素的影响。模型底部为全约束，侧面为法向约束。岩土体材料及结构面均采用Mohr-Coulomb屈服准则，节理末端条件在地表设为“端部张开”，其余全为“端部闭合”。各级岩体根据风化线进行模拟，地质构造则主要模拟了断层F8和F10。由于边坡整体位于地下水位以上，且库水位也较低，计算过程中不考虑地下水的影响。将边坡岩土体强度参数(内摩擦角和黏聚力)的不确定性纳入点估计概率模型(仅考虑花岗岩和新近系红层)。根据Rosenbluth点估计法的原理可知，此次共有8个随机变量，将形成28即256种组合方式，分别计算每种组合方式下的边坡稳定性系数，根据式(4)～式(7)即可得到边坡稳定性系数的平均值、标准差、可靠性指标及破坏概率。岩土体及结构面参数取值见表2、表3。

表1 结构面几何特征参数Table 1 Geometric characteristic parameters of structural plane

表2 岩土体参数取值Table 2 Parameter value of rock and soil mass

表3 结构面参数取值Table 3 Parameter value of structural plane

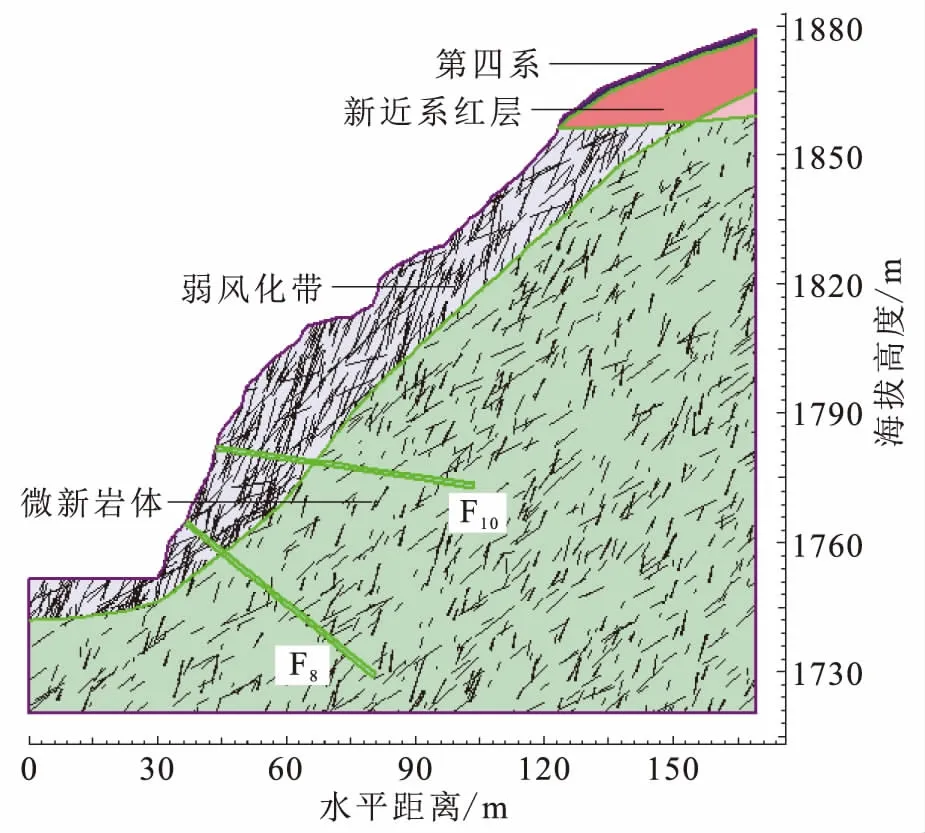
图2 生成的节理网络模型Fig.2 Generated joint network model

3.3 计算结果及分析

采用基于Rosenbluth点估计法的节理有限元强度折减对该边坡进行稳定性分析，计算得到边坡在天然工况下的稳定性系数最大值为2.24，最小值为1.61，平均值为1.93。而未添加节理网络的边坡稳定性系数为2.28，增加了18.13%。图3为边坡稳定性系数的概率分布图，可见其分布符合正态分布规律。根据Rosenbluth点估计法得到边坡稳定性系数的标准差为0.125 5，变异系数为0.065，可靠性指标为7.417，破坏概率为0.001‰，表明该边坡发生整体失稳的可能性较小。图4为添加以及未添加节理裂隙网络的边坡模型处于临界状态时的最大剪应变云图，可以看出，未考虑节理裂隙网络的边坡模型最大剪应变集中带主要位于弱风化带附近，而考虑了节理裂隙网络的边坡模型的剪应变集中带在中上部更加靠近坡面。图5为对应的总位移云图，由于裂隙的发育，岩体呈现出明显的非均质性和各向异性，位移等值线总体呈追踪陡倾结构面和缓倾结构面发展的“阶梯”状。临界状态下弱风化带内的节理大部分屈服(图6中红色直线)，微新岩体中屈服的节理相对较少。图7为边坡岩体沿节理的剪切运动局部图，红色箭头指示岩块的相对运动方向，随着缓倾节理屈服，岩块向临空方向产生滑移，坡体内应力重分布，与缓倾节理相互交切的陡倾节理产生相应屈服并逐渐产生拉裂，岩块被剪出。

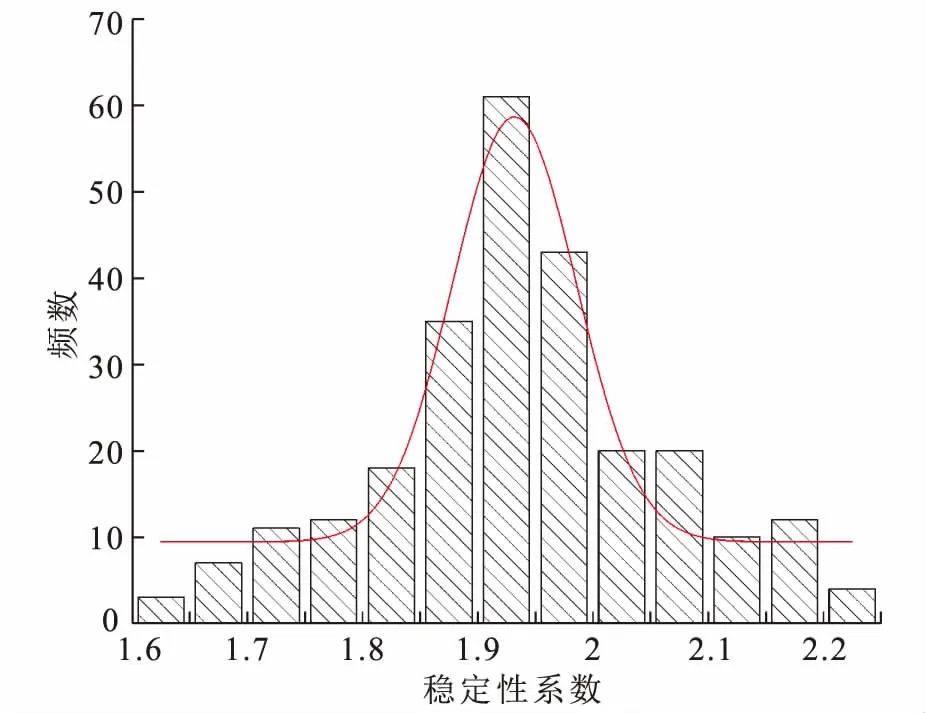
图3 边坡稳定性系数概率分布图Fig.3 Probability distribution of slope stability coefficient

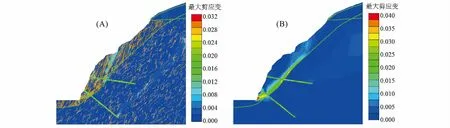
图4 最大剪应变云图Fig.4 Nephogram of maximum shear strain (A)添加节理裂隙网络(SRF=1.93);(B)未添加节理裂隙网络(SRF=2.28)

图5 总位移云图(SRF=1.93)Fig.5 Total displacement nephogram

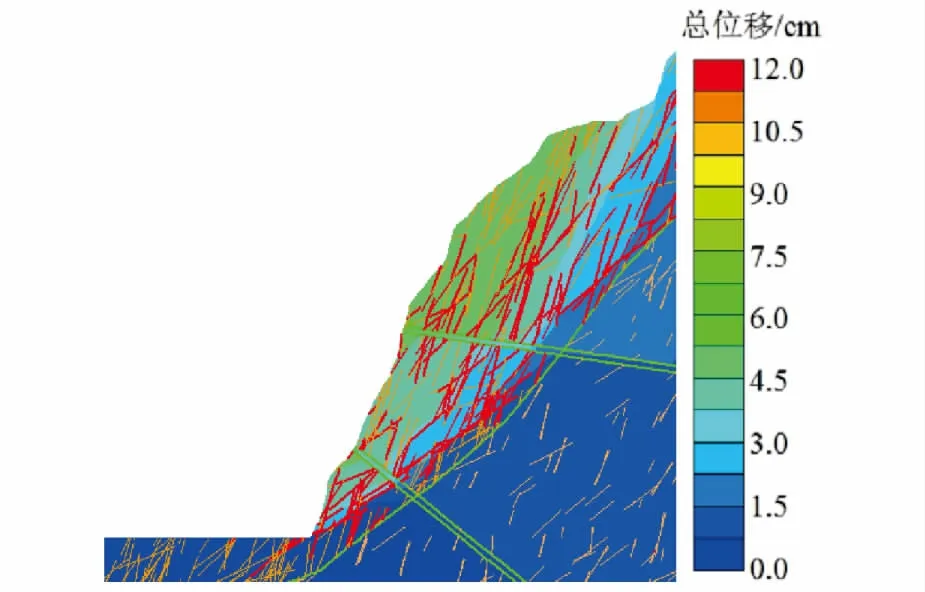
图6 屈服节理图(局部)Fig.6 Yield joint diagram (local)

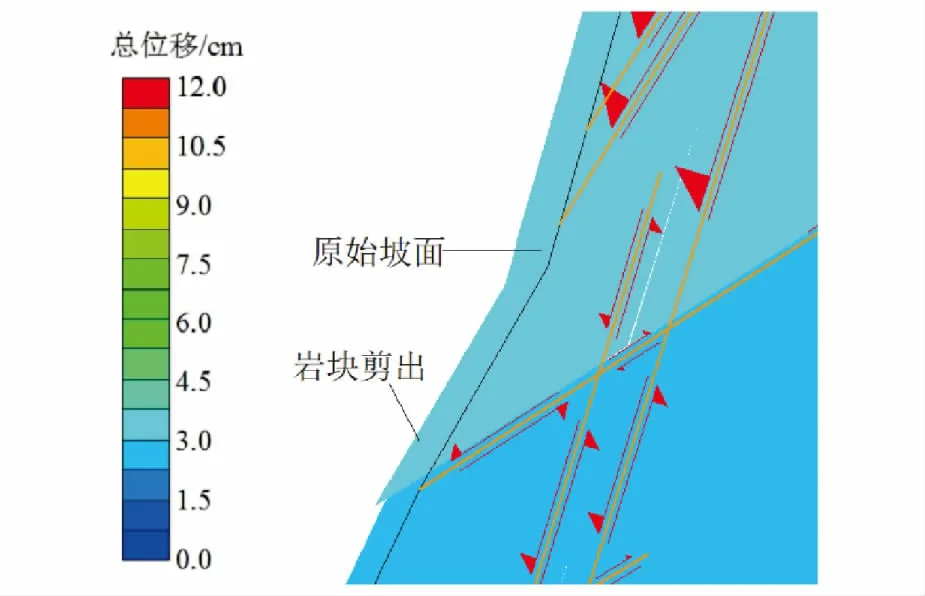
图7 边坡岩体沿节理的剪切运动Fig.7 Shear movement of slope rock mass along joints

综合以上分析表明，采用有限元节理网络得到的边坡稳定性系数更为保守，现状条件下，该边坡整体稳定性较好，其潜在变形破坏模式为沿着结构面发生的“阶梯”式滑移-拉裂破坏。此外，由于受到结构面相互切割的影响，在坡表面处可能存在一些不稳定楔形块体以“滑移-拉裂”的形式剪出。

4 结论及建议

a.有限元节理网络将岩体定义为由岩块和节理组成的二元结构，能够较好地反映结构面随机发育的特征，建模便捷且计算分析省时，可作为除离散元法以及等效连续介质法以外的又一种节理岩质边坡稳定性计算的途径。

b.运用Rosenbluth点估计法充分考虑岩体强度参数变异性，将稳定性系数和概率评价相结合，使得到的边坡稳定性系数更为合理、精确。

c.本文以中国西部某电站左岸坝肩边坡为例进行计算分析。结果表明，现状条件下该边坡整体稳定性较好，但浅表部有部分岩体由于风化以及结构面相互切割的影响，易形成不稳定楔形块体以“滑移-拉裂”的形式剪出。

d.建议对该边坡采取如下防治措施：清理表面危石；在重点区域挂设主动防护网，然后结合主动防护网喷混凝土将表面裂隙封闭；对于局部不稳定块体，采用锚杆+预应力锚索进行随机支护，并在下方增设被动防护网。