基于双向长短期记忆神经网络的岩相预测方法
熊玄辰,曹俊兴,周 鹏,许汉卿,程 明
(油气藏地质及开发工程国家重点实验室,地球勘探与信息技术教育部重点实验室(成都理工大学),成都 610059)
岩相信息能够反映岩层发育情况和储层特征,是地震储层预测的基础性工作。常规岩相预测方法多为基于弹性参数定性或定量地解释岩相信息。叠前地震反演技术作为实际应用中获得弹性参数的主要方法,难以避免多解性和不稳定性。近年来基于贝叶斯理论的岩相反演方法作为一种基于叠前弹性参数的自动解释方法也开始用于岩相预测。基于贝叶斯理论联合测井数据与地震数据进行基于叠前地震数据的反演方法被广泛认为能够预测岩相[1-3]。另一类常用的岩相预测方法是基于地震波形的聚类分析进行复杂岩相的预测[4],这类方法建立在精确时深匹配的基础之上;可是实际岩相与地震波形间的响应机制受构造、流体等其他因素影响,很难一一对应[5]。
深度学习的概念最早由G.E.Hinton等[6]提出,深度学习模型是用机器学习的思想从样本数据中训练得到的包含多个层级的深度网络结构[7-8]。作为最成功的深度学习模型之一,循环神经网络(Recurrent neural network,RNN)[9]最大的特点是拥有记忆能力。相较于其他网络结构,RNN善于挖掘样本之间的相互关系,在处理序列数据方面颇具优势。作为改进RNN的一种,长短期记忆神经网络(Long short term memory neural networks,LSTM)[10]利用门控单元解决了常规 RNN中梯度消失、梯度爆炸等问题[11],已有学者运用LSTM网络方法进行了孔隙度预测[12]、测井曲线钻前预测[13]等研究并取得了较好效果。双向长短期记忆神经网络(Bi-directional long short-term memory,Bi-LSTM)是在普通LSTM的基础上加入了双向传播的思想,让模型使用2个隐藏层分别处理正反两向输入的数据,再由2个隐藏层共同作用产生输出。在Bi-LSTM神经网络结构中,隐藏层神经元之间是有连接的,并且隐藏层的输入同时包含输入层的输出和上一时刻隐藏层的输出,两者一起决定隐藏层神经元状态。这与地层整体呈现出的沉积时序特性具有相似性,符合从已知推断未知的地质学基本研究方法和思想。
基于此,本文针对地震数据的非线性、序列性特性进行研究,介绍一种基于Bi-LSTM的岩相预测方法,将其应用于四川某浅层河道砂体勘探区岩相预测。结果表明,Bi-LSTM模型能够有效学习输入地震数据中的岩相特征,实现岩相预测。
1 方法原理
1.1 RNN
在传统的人工神经网络中,同一个隐藏层的神经元是不能交叉连接的,无法全面地连接序列信息,这意味着在训练过程中以前的神经元计算结果不能影响当前神经元的计算,前后序列信息无法有效结合。RNN的结构利用先前时间的信息记忆作用于当前神经元的计算,达到连接隐藏层中神经元的目的。利用典型的RNN单元(图1),可以有效地解决序列信息的问题。
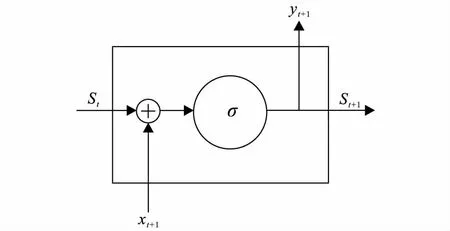
图1 RNN单元结构Fig.1 Structure of RNN
在RNN结构中,当前时间步的输出受之前时间步的影响且作用于之后时间步的计算,也就是说RNN的输出由同一网络上的多个时间序列相互影响产生,参数在不同时间共享。我们设输入序列为X={x1,x2,…,xm},隐藏层序列为S={s1,s2,…,sm},输出层序列为Y={y1,y2,…,ym}。则Y的计算过程为
St=σ(WXS+WSS+bS)
(1)
Yt=WSYSt+bY
(2)
式中:t为当前序列时间;σ()为Sigmoid函数;WXS为连接输入层和隐藏层的权重系数矩阵;WSS为隐藏层之间的权重关系矩阵;WSY为连接隐藏层与输出层矩阵的权重系数;bS为隐藏层的偏移矢量;bY为输出层的偏置。t时刻的隐藏层是通过t-1时刻隐藏层神经元的输出和t时刻隐藏层神经元的相应计算得到的。得益于隐藏层神经元在内部计算过程中不断增加数值的维数和范围,模型才能具有更复杂、更精确的非线性映射能力,并在有限网络基础上展开更精确的预测。
从理论上讲,RNN可以很好地解决序列数据的问题,但也存在以下问题[14]:①虽然RNN的设计结构可以用于预测整个时间序列,但其传输存储信号总的来说呈现下降趋势。一些需要处理的复杂序列数据丢失了网络的起始序列信息,导致RNN在长期依赖性问题上存在劣势。②RNN在多层网络中训练长序列会产生梯度消失和爆炸。为了克服这些问题,引入了LSTM神经网络。
1.2 LSTM
标准RNN采用重复链式结构,而LSTM的结构(图2)与RNN类似,但在重复单元结构上有所不同。LSTM中引入了“门”的概念来控制隐藏单元间的相互转换计算,对记忆细胞进行连续的写、读和重置操作[15]。单元状态C是隐藏层处理的关键。LSTM从前到后的步骤都是对存储在单元状态C中的信息进行处理。利用交互层的3种“门”结构乘法单元和每个单元的激活函数,对当前时间的输入和先前隐藏单元的状态进行处理,过滤单元状态C中的无用信息并增加新的信息。
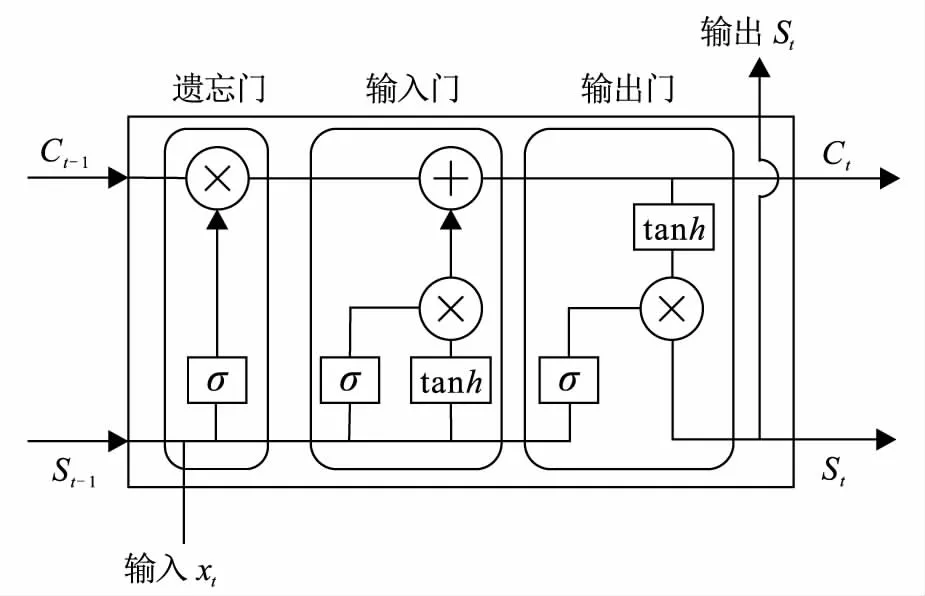
图2 LSTM单元结构Fig.2 Structure of LSTM(据S.Hochreiter等[10])
一个LSTM单元中的第一个交互结构为遗忘门,用来选择和保留过去状态Ct-1和当前状态Ct中的信息。遗忘门的表达式为
ft=σ(Wf[st-1,xt]+bf)
(3)
式中:中Wf为遗忘门的权重系数矩阵;σ()为Sigmoid函数;bf为偏置;ft为遗忘门的决策向量。
第二个交互结构为输入门。输入门控制前序信息向当前单元状态C的传输,并处理当前输入的序列信息。输入门有2个模块,第一个模块用于确定信息的更新状态,第二个模块利用tanh函数确定当前时刻更新的候选信息。
it=σ(Wi[st-1,xt]+bi)
(4)
(5)

第三个交互结构为当前时刻单元状态Ct的计算结构,它通过遗忘门和输入门的决策来决定信息的增加和删除。
(6)
⊙为求哈达玛积。
最后一个交互结构为输出门。Sigmoid函数用于确定当前状态的输出决策,tanh函数确定当前单元状态的输出信息。输出决策与输出信息相乘得出本时刻需要输出的信息。
Ot=σ(Wo[st-1,xt]+bo)
(7)
St=Ot⊙tanh(Ct)
(8)
式中:St为输出的隐藏状态;σ()为Sigmoid函数;Wo和bo分别为输出门的权重系数矩阵和偏置。
LSTM训练的主要算法是反向传播算法,需要注意以下3点:①每个神经元在向前传播时的输出都是ft、it、Ct、Ot和St;②在LSTM中,误差项通过反向计算传播;③每个权重的梯度用相应的误差项来计算。
LSTM使用“门”结构的概念来控制RNN中每个时刻单元层的状态。将这些单元层的特征应用到网络中,优选保留需要长期处理的有效信息,有效地解决了RNN在处理长时间序列中梯度消失和爆炸的问题。
1.3 Bi-LSTM
M.Schuster等[16]提出了双向 RNN (BRNN) ,采用双向传播的方法,让模型使用2个隐藏层分别处理正反两向输入的数据,再由2个隐藏层共同作用产生输出。BRNN的展开形式如图3所示。

图3 BRNN结构Fig.3 Structure of BRNN(据M.Schuster等[16] )
Bi-LSTM将BRNN和LSTM的优点结合,将LSTM门控记忆单元运用到BRNN的双向传播模型中。(9)式~(11)式是前后隐藏层、输出层的具体计算过程。其中:W、V、U为权重矩阵;b、c为偏置;ht表示t时刻单向隐藏层的输出;yt表示t时刻隐藏层的输出[17]。
(9)
(10)
(11)
Bi-LSTM理论上可以让模型在预测当前岩相的时候能够同时利用到整个输入序列的信息。
2 基于Bi-LSTM的预测方法
本文采用已钻井地层的测井数据和井旁道地震吸收衰减数据训练模型,预测未钻井区域的岩相发育情况。地震吸收衰减数据是伴随地层的非弹性性质产生的现象,不同岩相的地震吸收衰减数据效应存在差异[18]。为了最大限度利用地震数据中的有利信息,对不同角道集叠加后的地震属性进行分析,发现远道叠加减近道叠加后的地震高频吸收衰减能够反映全叠加高频吸收衰减无法反映的岩相信息。图4分别为B井附近的全道叠加高频吸收衰减属性剖面和远道叠加减近道叠加后的地震高频吸收衰减剖面,红色箭头标出了吸收衰减属性对砂岩相的明显指示区域,可以看出全道叠加高频吸收衰减属性和远道叠加减近道叠加后的地震高频吸收衰减指示不同的砂岩相特征。

图4 B井不同叠加高频吸收衰减属性分析图Fig.4 Attribute analysis of high frequency absorption with different stacking in Well B
通过岩石物理分析发现,研究区的砂岩相和泥岩相无法通过密度、纵波阻抗和伽马拟声波阻抗进行有效区分。将以上3种属性和地震吸收衰减同时作为变量输入深度学习模型,利用深度学习提取非线性关系的能力找出输入数据与岩相间的复杂关系,来达到预测岩相的目的。从岩石物理分析可知,输入变量无法通过简单的阈值清晰划分岩相,需要提取不同输入变量间的复杂非线性关系来获取岩相信息。而处理多变量预测,挖掘不同变量间的关系正是Bi-LSTM的强项。对于单独变量,每一个样本点的岩相不仅与当前时间点的输入变量值相关,在纵向上输入变量的变化趋势也有反映。与常规的时间序列数据不同,单点的岩相信息不仅与该点上方的地层相关,也与该点下方的地层相关。相比单向传播的方法,Bi-LSTM的双向传播方法能综合利用上下地层的关系来预测目标岩相,获得更充分的岩相信息。岩相在每个时间深度都与一定时窗内的相邻地震数据相关,因此选择“点-窗”的匹配采样方法(图5)。通过实验测试优化,最终确定每一个岩相对应上下3 ms的测井密度、纵波阻抗和伽马拟声波阻抗及上下3 ms、9个井旁道的地震吸收衰减数据属性建立一个样本。
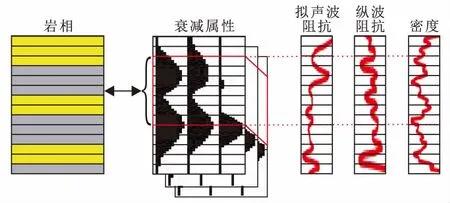
图5 样本构建示意图Fig.5 Sketch showing the sample configuration
本文建立的Bi-LSTM预测模型为
(12)
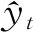
本文构建的Bi-LSTM模型如图6所示,包含输入、隐藏和输出层。原始输入数据经过预处理后输入到输入层,然后传递到隐藏层。在输入层,Relu激活函数调整传入隐藏层的参数大小,使处理后的数据符合神经网络的输入维数要求。隐藏层由3层Bi-LSTM组成,每层Bi-LSTM包含正向和逆向2个LSTM层。隐藏层中上一个输出序列为当前层的输入。隐藏层正向初始化单元状态S1.0和C1.0通过第一个LSTM单元后输出S1.1.1和C1.1.1给下一个LSTM单元,逆向LSTM以同样原理反向传输,同一位置的正、逆向LSTM单元共同输出S1到下一个隐藏层作为输入层。通过这样的循环运算输出最后的隐藏层预测序列(p1,p2,…,pL)输出到全连接层得出预测岩相。预测采用层数叠加的模型构建方法,相比单层的Bi-LSTM能够更好地挖掘序列信息的变化趋势。通过多个“门”结构的控制,有效过滤无用信息,最大限度保留了地震吸收衰减数据的特征信息,提高岩相预测的准确性。
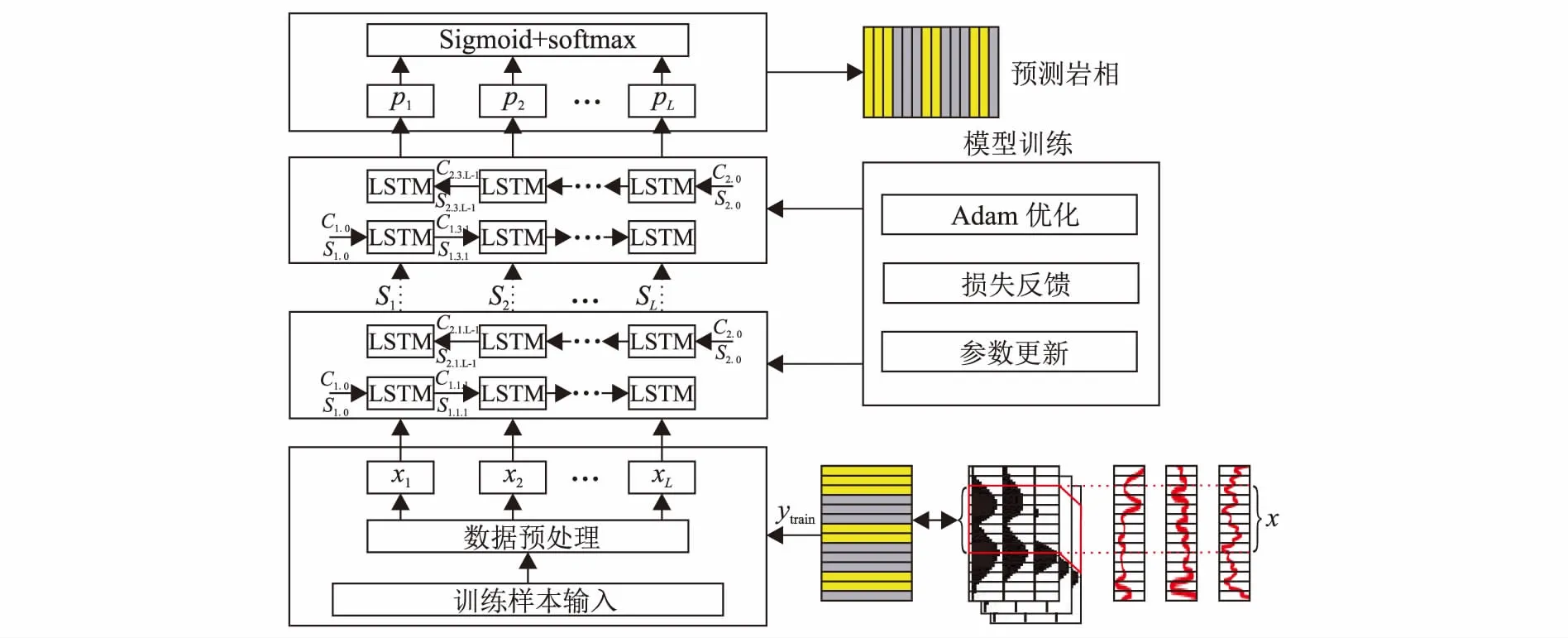
图6 Bi-LSTM预测模型Fig.6 Bi-LSTM prediction model
2.1 数据预处理
本文采用minmax-scale的方法对输入数据做归一化处理,确保地震吸收衰减数据处于合理的分布范围之内。计算公式为
(13)
式中:Xscaled为归一化后的地震吸收衰减数据;X为地震吸收衰减数据;a和b分别为给定缩放范围的上下限,本文中为1和0。经过归一化处理的输入数据保留了原始数据中的相关关系,且能消除输入数据中异常值的影响。
2.2 优化算法
优化算法的合理运用能大幅度提高训练的效率。本文选择了具有自适应学习率的Adam算法。Adam算法结合了AdaGrad算法[19]在稀疏梯度处理上的优点和RMSprop算法[20]对欠稳定目标处理的优点,确保了算法精度和稳定性。具体来说,Adam算法通过对稀疏参数的更新幅度增大,频率参数的更新幅度减少,用最少的训练迭代次数达到网络的最优效果。
2.3 损失函数确定
本文选取了更适合分类优化算法的最小化交叉熵的方法计算损失函数
(14)
其中:J表示损失函数;yi是类别i的真实标签;Pi是上面softmax计算出的类别i的概率值;k是类别数;N是样本总数。在此用一个小例子来说明交叉熵计算原理。假设一个三分类问题,将目标样本分为A、B、C三类,那么一个A的样本标签应该为(1,0,0)。如果经过网络预测后得到的输出为(3,1,-3)。经过softmax可以得到对应的概率值如图7所示。

图7 交叉熵计算原理示意图Fig.7 Schematic diagram showing cross entropy calculation principle
上例中交叉熵损失为
J=-(1×lg0.88+0×lg0.11+0×lg0.01)=-lg0.88
综上,本文通过引入交叉熵损失函数,配合Sigmoid激活函数,可以有效优化分类问题的深度学习网络模型。
2.4 预测结果评价
本文采用准确率(accuracy)评价预测结果。准确率直接反映模型预测岩相的准确度。准确率计算公式如下
(15)
式中:A为准确率;ST为预测正确的样本数;S为样本总数。
3 应用与分析
3.1 实验概述
研究区为四川某浅层砂泥岩勘探区,存在A、B、C共3口钻井。根据钻井资料,将研究区目标层位岩相划分为泥岩相和砂岩相。研究区目的层河道砂体发育,岩相预测对后续的河道雕刻具有一定指示作用。目的层砂泥岩在纵波阻抗、密度、伽马值等常规参数上无法有效区分,利用现有钻井资料难以有效开展岩相预测。A井上段为中厚层砂岩相与泥岩相互层,下段发育厚层砂岩相;B井砂岩相发育良好,有少部分中厚层泥岩相;C井上段和中下段发育2套厚层砂岩相,其余部分均为砂岩相与泥岩相互层。本文将A、B井作为训练集进行模型训练,C井作为测试集进行模型评估。引入普通RNN和普通LSTM以相同超参数搭建网络模型进行训练预测,与Bi-LSTM模型进行对比。
本文模型训练采用的计算机配置如下:GPU为Quadro GP100,内存为1 TB。网络构建基于TensorFlow。实验的超参数见表1。

表1 实验的超参数Table 1 Hyperparameters of the experiment
3.2 应用效果
图8、图9分别为A井、B井的模型拟合结果。从训练集拟合的预测结果可以看出,训练集的预测岩相与真实岩相基本对应,说明模型已经学习到了岩相特征。从图8可以看出,A井在模型拟合阶段岩相预测结果与真实岩相对应良好,模型拟合的预测误差主要集中在上段薄层;RNN的拟合结果丢失了大部分的薄层泥岩相特征,在这一点上LSTM与Bi-LSTM效果更好;在LSTM的基础上,Bi-LSTM的预测结果更精细,与真实岩相对应更好。从图9可以看出,RNN在B井的拟合同样丢失了一部分泥岩相的特征(1 400~1 424 ms);同样,LSTM与Bi-LSTM效果更好,且Bi-LSTM效果较LSTM更精细:说明双向传播的方法有利于提取输入数据中的岩相信息。

图8 A井拟合结果Fig.8 Fitting results of Well A

图9 B井拟合结果Fig.9 Fitting results of Well B
图10为C井的预测结果,可以看出预测岩相与真实岩相基本对应,预测误差集中在薄层砂岩相。从预测的准确率(表2)可见Bi-LSTM测试准确率高于RNN和LSTM;相较于RNN,LSTM和Bi-LSTM能够选择性地记忆部分特征,对信息进行判断和筛选,能够更高效地提取输入数据中蕴含的岩相特征。在Bi-LSTM网络结构中,由于输入的信息可以在网络中正反两向传递,其内部的权重更新更贴合岩相纵向上的动态变化特征;因此,Bi-LSTM模型能够充分利用岩相随地层的变化趋势,实现比RNN和LSTM更精确更稳定的岩相预测。

表2 实验准确率Table 2 Accuracy of the Experiments
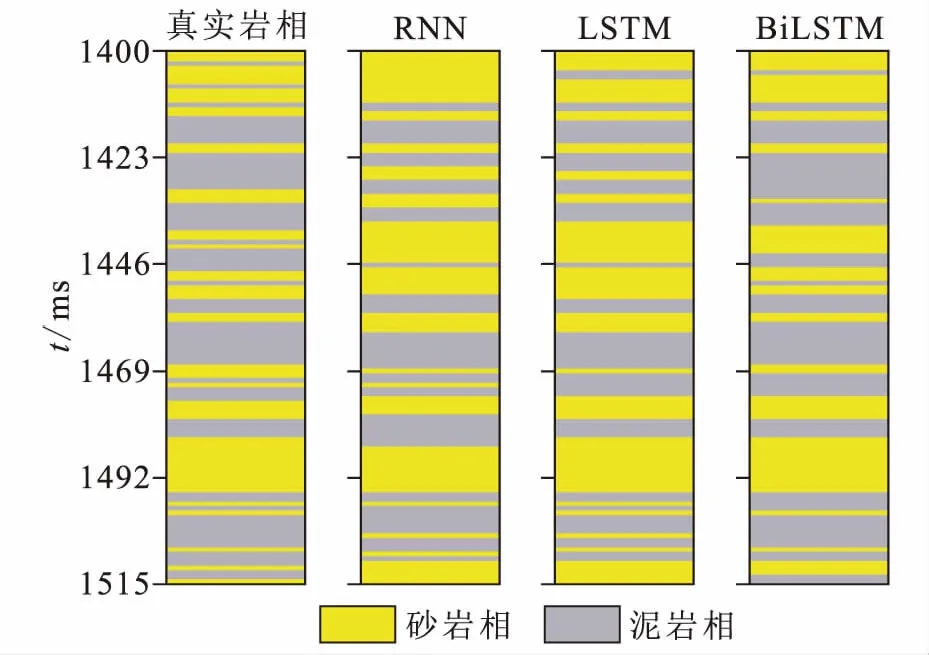
图10 C井测试结果Fig.10 Test results of Well C
图11为测试剖面的原始地震剖面,图12为Bi-LSTM模型预测的岩相剖面。未钻井区预测使用反演的密度、纵波阻抗和伽马拟声波阻抗及地震吸收衰减数据作为输入。根据工区相关资料,已知层3处有一条从A井到B井的河道砂体,与预测剖面的结果符合。预测剖面砂体刻画清晰,符合砂岩相的地下分布特征。
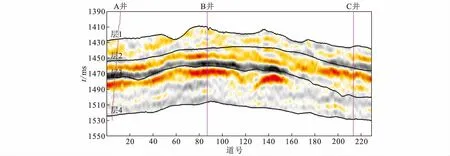
图11 原始地震剖面Fig.11 Original seismic profile
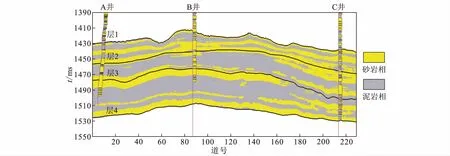
图12 Bi-LSTM预测岩相剖面Fig.12 Bi-LSTM prediction of lithofacies profile
为了更好地展示模型预测岩相在横向上的指示能力,使用沿层切片方法对深度学习模型预测结果进行分析。图13为层2底部的深度学习模型岩相预测结果的沿层切片,从切片结果可以看出,深度学习模型的岩相预测结果对砂体的平面展布有良好的指示性,砂体的分布符合研究区砂体分布地质规律。模型对大面积砂体的刻画较好,从结果中能够清晰展现砂体的边界。同时,模型也具有对小块砂体的识别能力,小块砂体的形态刻画明确,结合其他属性进行分析对后续的勘探工作具有良好的参考性。
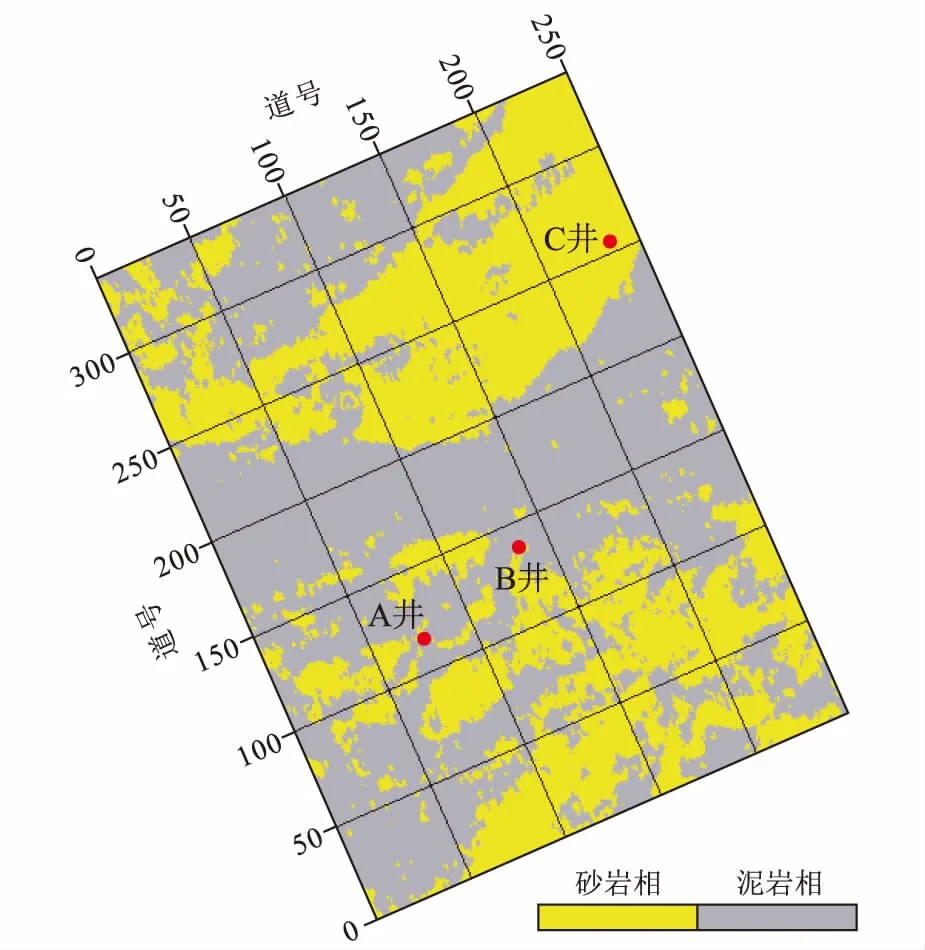
图13 层2底部岩相预测结果切片图Fig.13 Slice diagram of lithofacies prediction results at the bottom of layer 2
图14为层3底部的深度学习模型岩相预测结果的沿层切片,从切片结果可以明显看出两条砂体河道,河道形态明显,连续性好。此结果证明该方法对于河道砂体有较好的识别能力,能够有效揭示地下河道砂体的发育形态。
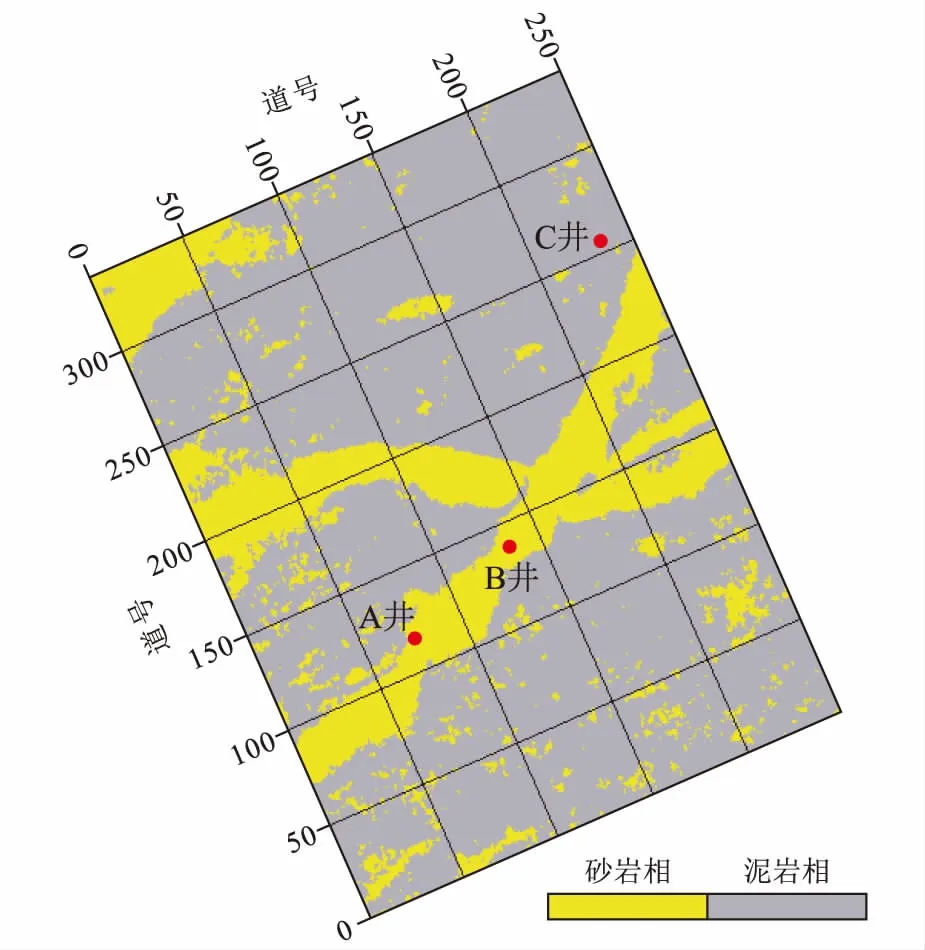
图14 层3底部岩相预测结果切片图Fig.14 Slice diagram of lithofacies prediction results at the bottom of layer 3
4 结 论
a.基于地震的岩相预测是油气地震勘探的基础性工作。本文基于Bi-LSTM的岩相预测方法,得益于Bi-LSTM双向传播的优势,充分利用输入数据随深度的变化趋势和前后关联,提取岩相与输入数据的非线性映射关系。训练好的Bi-LSTM模型在实际数据测试中取得了较好结果,能有效揭示地下岩层发育情况,有利于地层分析和储层预测。
b.虽然基于Bi-LSTM的岩相预测取得了一定效果,但仍存在识别分辨率低、部分预测岩相不准确的缺陷。本文采用的深度学习模型较单一,多模型混合运用能否提升模型预测效果有待进一步研究。

