带子矩阵约束的二次逆特征值问题的最小二乘埃尔米特广义斜哈密顿矩阵迭代解

杨 娇,杨 吉,黄光鑫,尹 凤

(1.成都理工大学 数学地质四川省重点实验室 数理学院，成都 610059;2.四川轻化工大学 数学与统计学院，四川 自贡 643000)

1 引 言

逆特征值问题在科学与工程计算中具有广泛的应用，也是近期国内外研究热点[1-2]。二次逆特征值问题是一类重要的逆特征值问题。二次逆特征值问题可以描述为：

AXΛ2+BXΛ+CX=0

成立。

近几年，国内外许多专家学者研究了二次逆特征值问题的不同解。Z.J.Bai[3]解决了逆特征值问题的埃尔米特广义斜哈密顿解。J.Qian等[4]给出了特征值反问题的埃尔米特广义哈密顿/斜哈密顿矩阵。J.Tang等[5]研究了带子矩阵约束的二次逆特征值问题的最小二乘广义斜哈密顿矩阵解。本文考虑带子矩阵约束的二次逆特征值问题的数值解。

在给出所研究的问题之前，我们首先给出如下符号说明和定义：

定义 1给定任意J∈An×n，

带子矩阵约束的二次逆特征值问题及其最佳逼近问题可以描述为：

‖A*XΛ2+B*XΛ+C*X‖=min‖AXΛ2+BXΛ+CX‖

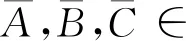
本文主要研究带子矩阵约束的二次逆特征值问题的最小二乘解问题1及其最佳逼近问题2的迭代算法，进而给出问题1和2的迭代解。

2 求解问题1的迭代算法

我们注意到，问题1的解集不是一个线性子空间。一些有效的迭代算法不能直接应用于问题1的求解。为此，我们首先将问题1的解集进行等价转换。记

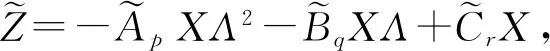
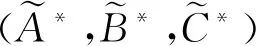
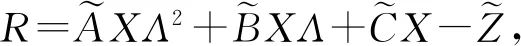
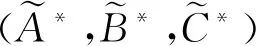
算法1(CGLS迭代算法)

步骤1计算

记k=1。

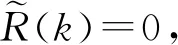
步骤3计算:

P(k)=T1(k)XΛ2+T2(k)XΛ+T3(k)X,

Q(k)=(Q1(k) 0 0;0Q2(k) 0;0 0Q3(k))

更新序列:

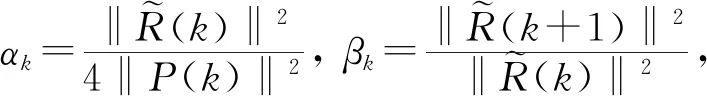
T(k)=(T1(k) 0 0;0T2(k) 0,0 0T3(k))。

步骤4记k=k+1,返回步骤2。

为了建立CGLS算法的收敛性，我们首先给出算法1的一些基本性质。

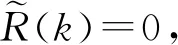
定理 3在不存在舍入误差的情况下,算法1最多经过3n2次迭代，可得到问题3的最小二乘解。

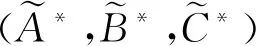
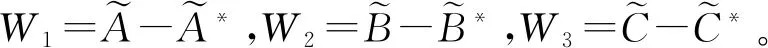
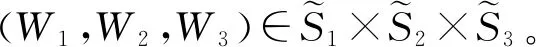
满足

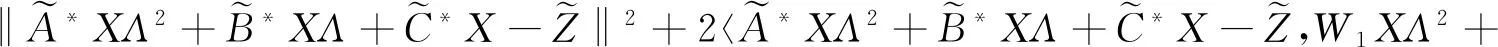
W2XΛ+W3X〉+‖W1XΛ2+W2XΛ+W3X‖2

因此，W1XΛ2+W2XΛ+W3X=0成立。

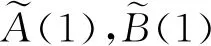
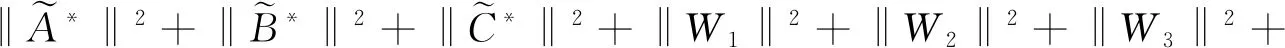
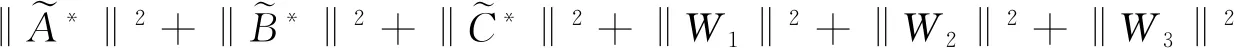
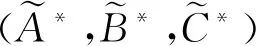
3 求解问题2的迭代算法

由上式可知，最小化问题

的解等价于如下最小F范数解

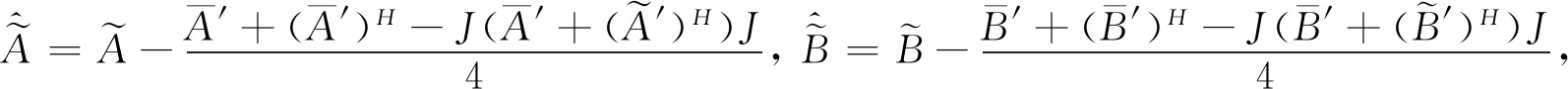
4 数值实例

考虑到舍入误差的影响,如果〈T,T〉<10-15，我们将矩阵T视为零矩阵。实验在Matlab 6.5.1环境下进行。

例1考虑二次逆特征值问题

AXΛ2+BXΛ+CX=0

其中：

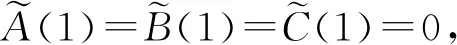
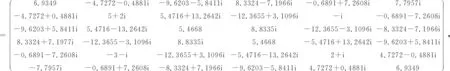
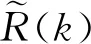
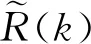
图1 R(k)的范数的收敛性Fig.1 The convergence of the norm of R(k)

图2 的范数的收敛性Fig.2 The convergence of the norm of

5 总 结

本文给出了一种带子矩阵约束的二次逆特征值问题及其最佳逼近问题的共轭梯度迭代算法,分析并证明了算法的收敛性。