单双边混合数据下比例比的渐近置信区间构造
覃 愿,伏启翔,刘青松,邱世芳
(重庆理工大学 理学院,重庆 400054)
在生物医学和流行病学研究中,成对身体器官(如耳朵,眼睛,肾脏)或身体成对部位(如手臂和脚)的治疗数据通常是高度相关的。因而忽略了它们之间的相关性的统计推断,常常会得到不合理的研究结果[1-3]。对于成对器官都患病的情形(即双边试验数据)下,考虑到来自成对器官或身体部位的高度相关性,Rosner[1]分别在独立和非独立模型下考虑了2种治疗等价性评价的2种卡方检验统计量,Rosner等[2]考虑了基于相关二分类数据的显著性检验,Tang等[4]考虑了基于比例差提出了独立和非独立模型下的8种检验统计量,并提出了基于这些检验统计量的近似非条件的检验过程。并在此基础上,Qiu等[5]给出了基于这些检验的样本量的估计公式,Tang等[6]给出了比例差(治愈率之差)的各种置信区间方法。Pei等[7]基于相等相关系数模型下给出了2种治疗方案等价性评价的3种渐近检验过程。邱世芳等[8]从区间估计的角度给出了给定置信水平下区间宽度控制的样本量的估计公式。对于分层设计下的组内相关数据,Tang等[9]基于比例差考虑了分层等价性评价的score等检验统计量以及score齐性检验,Pei等[10]在相等相关系数模型下考虑了基于比例比的齐性检验以及样本量的确定。Qiu等[11]基于反双曲正切变换的WLS检验统计量、修正的score统计量等多个统计量,研究了分层双边数据下基于比例差的齐性检验问题和样本量的确定。Qiu等[12]进一步研究了双边试验设计下比例差的同时置信区间以及齐性假定下共同比例差的置信区间构造问题。
以上研究都是只有双边数据下2种治疗的等价性检验等问题。然而,在临床试验中,观测数据通常既包含单边数据(个体的成对器官中的1个器官或成对身体部位的一部分接受治疗后所收集到的数据),又包含双边数据(个体的成对器官或成对身体部位都接受治疗后所收集到的数据)。例如,在耳鼻喉科(或眼科)的临床研究中,患病群体中一些人有2只耳朵(眼睛)患病并接受治疗,而另一些人只有1只耳朵(眼睛)患病并接受治疗。一个典型的例子就是Mandel等[13]关于儿童中耳炎疾病的双盲临床试验中,研究者将接受治疗的214个儿童(共计293只患病耳朵)随机分配到2个使用了不同抗生素药物(Cefaclor和Amoxicillin)的治疗组中,每个儿童都接受为期14 d的治疗,14 d治疗后治疗结果分为3类:① 患者的2只耳朵都被治愈;②患者只有1只耳朵被治愈;③患者的2只耳朵都没有被治愈。此临床试验数据如表1。

表1 接受14 d治疗后儿童的中耳炎数据
在既有单边数据又有双边试验数据下,人们感兴趣的问题是2个不同的药物治疗组(Cefaclor和Amoxicillin)对于该疾病的治愈率是否有显著性差异。对于混合的单边和双边数据,Pei等[14]分别在独立和非独立模型下考虑了基于比例差的等价性检验问题,提出了几种渐近的检验过程。本文在混合单边和双边数据下基于比例比从区间估计的角度研究2种治疗的等价性评价问题。同时,由于数据的离散性、稀疏性(有些格子观测频数很小或者为0)和高度相关性,渐近的区间估计在小样本下不一定有良好的统计性质,因而,本研究还考虑了基于Bootstrap重抽样的置信区间构造方法。目的是在小样本到大样本下给出简单有效的区间估计方法,为临床研究提供有效的统计方法。
1 数据结构与统计模型
一般地,以上单双边混合数据可归结为如表2的数据。

表2 单双边混合试验数据的观测频数及相应的概率
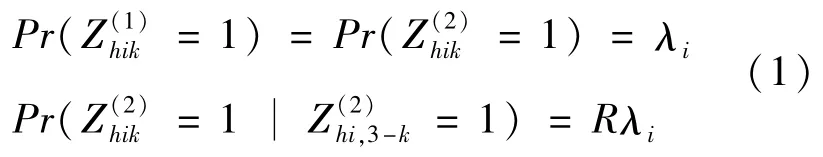
其中R是一个大于0的常数,并且是一个用来衡量患病的2只耳朵相关性的指标。特别地,当R=1时,表示2只耳朵完全独立,即1只耳朵治愈与否与另1只耳朵的治愈情况完全无关;当Rλi=1时,表示两只耳朵之间完全非独立。基于以上假设,易推导得到
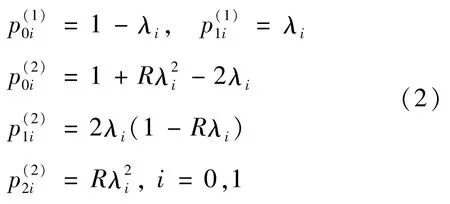
令 Δ=λ1/λ0,即 Δ为2个治疗组治愈率之比。在非独立模型下的对数似然函数为
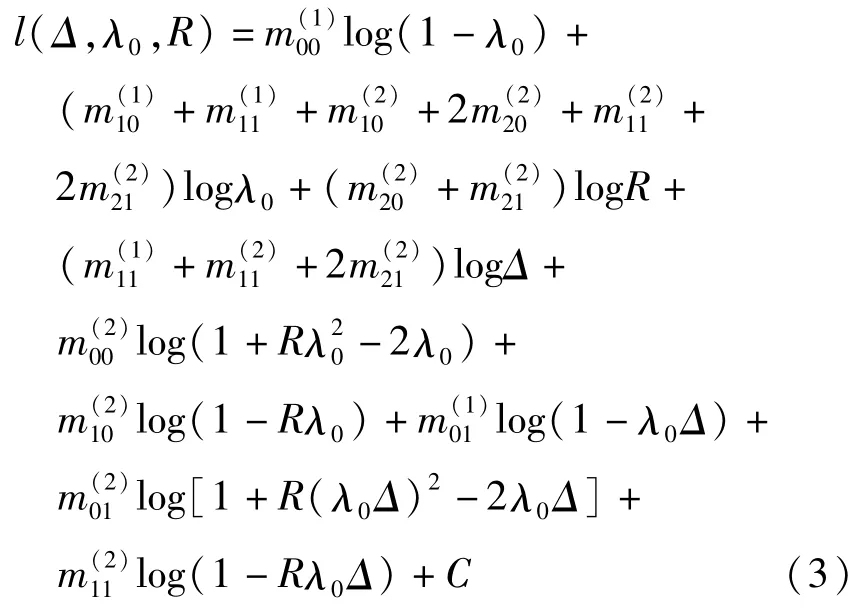
其中C是与参数Δ,λ0,R无关的常数。
本研究感兴趣的问题是Δ=λ1/λ0的渐近置信区间的构造,提出简单有效的区间估计方法。
2 置信区间构造
2.1 基于Wald检验的置信区间
基于对数似然函数(3),易得λ0和λ1的样本估 计 分 别 为则 Δ 的 样 本 估 计 为通过式(2)可得R的样本估计为通过Delta方法,可以得到的方差为
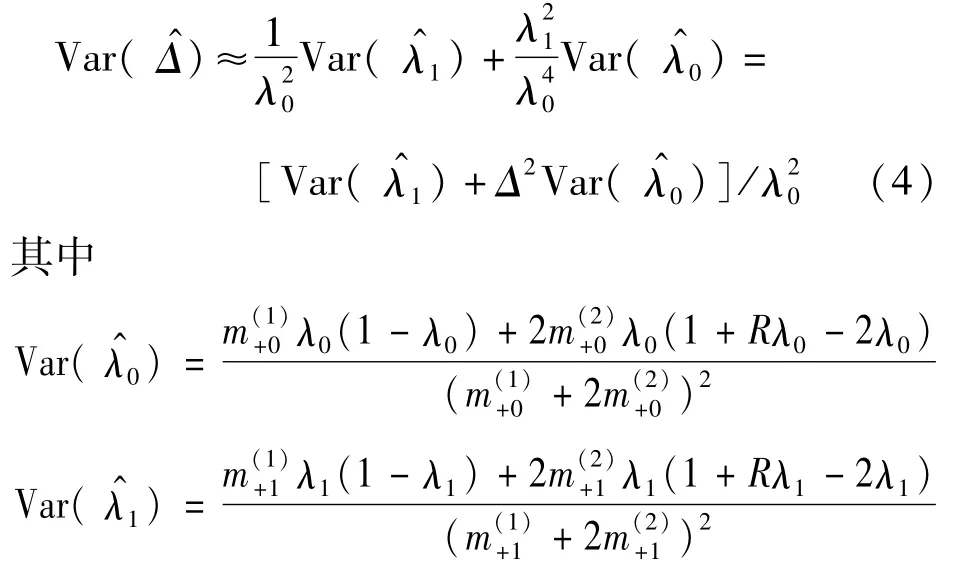
对于假设检验问题H0∶Δ=Δ0的Wald检验统计量为

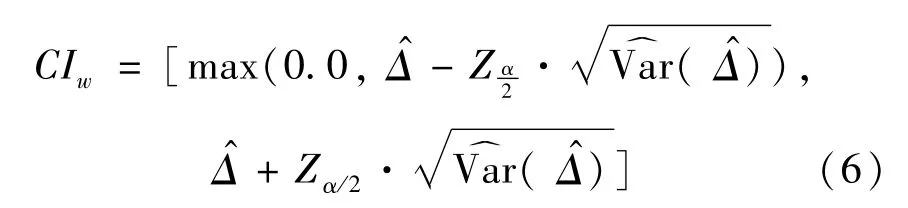
2.2 基于Wald检验的修正置信区间
由于在样本量较小的情况下,基于Wald的置信区间CIw的表现并不总是令人满意,因为它的经验覆盖率常常小于预先给定的置信水平1-α。根据Agresti等[15]所提出的小样本下Wald置信区间区间的修正方法,对表2中每个单元格加上0.5时得到修正的Wald置信区间,记为CIaw。
2.3 基于对数变换统计量的置信区间

根据Tang等的研究[7],对于假设检验问题H0∶Δ=Δ0的对数变换检验统计量为

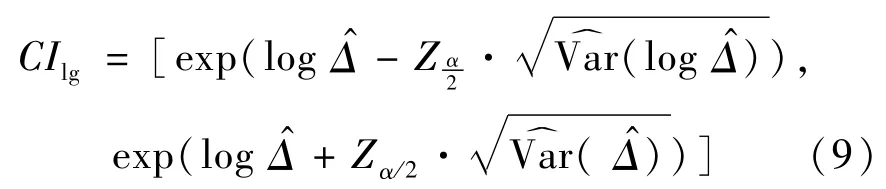
2.4 基于似然比检验的置信区间
在非独立模型(R≠1)下,对于假设检验H0∶Δ=Δ0的似然比检验统计量为


当样本量充分大时,Tl渐近服从自由度为1的卡方分布。因此,基于似然比检验统计量的Δ的100(1-α)%置信上下限为以下关于Δ0的方程的2个根:
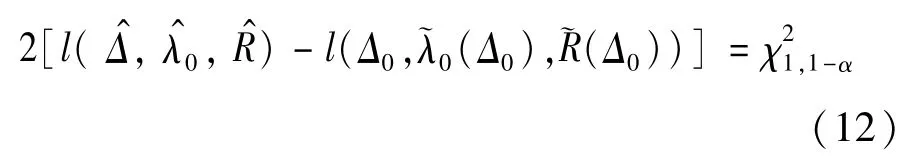
2.5 Bootstrap重抽样置信区间
上述的基于渐近方法的区间估计比较适用于大样本的情形,而当样本量较小时(即较小),基于渐近方法的区间估计可能并不十分可靠。因此,考虑小样本下都表现较好的Bootstrap重抽样置信区间,具体步骤如下:

3 模拟研究
为评价所提出的区间估计方法有效性,考虑如下样本量和参数设计的随机模拟:置信水平1-α=0.95,平衡样本量设计(20,20,20,20)、(50,50,50,50)和非平衡样本量设计=(20,30,30,20)、(30,50,50,30)以及参数设置:Δ=0.8(0.2)1.2,λ0=(0.3,0.5),R=0.8(0.2)1.2共18种参数组合。在每个样本量设置下,对每一种参数组合,通过重复模拟K次分别计算各种置信区间的经验覆盖概率、经验覆盖宽度以及左右非覆盖概率。经验覆盖概率、经验覆盖宽度以及左右非覆盖概率分别通过以下公式计算:
1)经验覆盖概率(ECP):
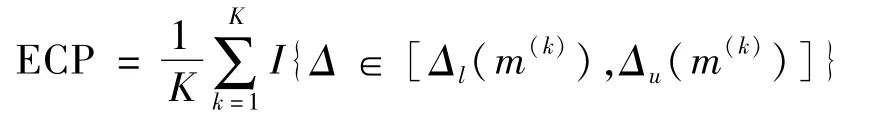
其中:[Δl(m(k)),Δu(m(k))]是 Δ的第k次模拟的置信区间;m(k)是第k次模拟的样本;I{·}为示性函数。
2)经验覆盖宽度(ECW):

3)左右非覆盖概率(LNCP,RNCP):
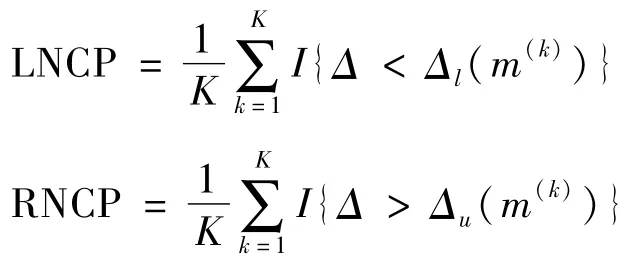
式中K=5 000,Bootstrap重抽样置信区间中B=1 000。模拟结果见表3~6。通过表3~6的经验覆盖概率、经验覆盖宽度和左右非覆盖概率,可以得到如下结论:

表3 小样本平衡设计(m(+1 0),m(+1 1),m(+2 0),m(+2 1))=(20,20,20,20)下的95%置信区间的经验覆盖率(ECP),左、右侧非覆盖率(L,R)和经验覆盖宽度(ECW)CIw CIaw CI lg CIl CI B Δ λ0 R ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW 0.8 0.3 0.8 93.50(0.18,6.32)0.97 95.76(0.18,4.06)0.94 95.22(2.44,2.34)1.03 95.36(2.14,2.50)1.04 94.30(2.40,3.30)1.09 1.0 93.40(0.08,6.52)1.00 95.66(0.12,4.22)0.96 95.30(2.58,2.12)1.07 94.06(2.20,3.74)1.06 94.32(2.62,3.06)1.13 1.2 93.36(0.08,6.56)1.02 95.36(0.10,4.54)0.98 94.62(2.80,2.58)1.10 93.66(2.48,3.86)1.10 94.08(2.62,3.30)1.17 0.5 0.8 94.74(0.64,4.62)0.61 96.14(0.62,3.24)0.60 95.30(2.60,2.10)0.63 96.40(1.88,1.72)0.71 94.72(2.50,2.78)0.64 1.0 94.44(0.80,4.76)0.65 95.92(0.80,3.28)0.64 95.26(2.46,2.28)0.67 96.48(1.56,1.96)0.74 94.68(2.36,2.96)0.68 1.2 94.20(0.76,5.04)0.69 95.58(0.80,3.62)0.67 94.76(3.02,2.22)0.71 96.08(1.92,2.00)0.78 94.46(2.70,2.84)0.73 1.0 0.3 0.8 94.08(0.10,5.82)1.13 95.42(0.10,4.48)1.06 95.36(2.62,2.02)1.18 92.22(2.44,5.34)1.13 95.44(2.60,1.96)1.27 1.0 93.54(0.14,6.32)1.16 94.78(0.12,5.10)1.09 94.92(2.40,2.68)1.22 90.28(2.68,7.04)1.13 95.02(2.40,2.58)1.31 1.2 93.68(0.08,6.24)1.20 94.84(0.08,5.08)1.12 95.40(2.32,2.28)1.27 89.66(2.36,7.98)1.16 95.34(2.32,2.34)1.37 0.5 0.8 94.42(0.72,4.86)0.67 95.30(0.50,4.20)0.66 94.84(2.44,2.72)0.68 96.54(1.72,1.74)0.81 95.08(2.46,2.46)0.70 1.0 94.14(0.68,5.18)0.73 94.92(0.48,4.60)0.71 94.82(2.34,2.84)0.74 95.98(2.06,1.96)0.84 94.94(2.28,2.78)0.77 1.2 93.96(0.70,5.34)0.77 94.88(0.52,4.60)0.75 94.64(2.82,2.54)0.79 96.00(1.92,2.08)0.88 94.98(2.68,2.34)0.82 1.2 0.3 0.8 94.46(0.04,5.50)1.27 94.70(0.00,5.30)1.18 95.04(2.18,2.78)1.33 87.20(1.84,10.96)1.16 94.02(2.96,3.02)1.45 1.0 94.58(0.04,5.38)1.31 94.84(0.04,5.12)1.21 95.52(2.10,2.38)1.38 84.34(2.14,13.52)1.15 94.50(2.94,2.56)1.50 1.2 93.84(0.04,6.12)1.36 94.20(0.04,5.76)1.25 95.02(2.26,2.72)1.43 81.72(2.32,15.96)1.15 94.10(2.98,2.92)1.56 0.5 0.8 94.36(0.72,4.92)0.73 94.82(0.40,4.78)0.71 94.92(2.14,2.94)0.74 97.08(0.88,2.04)1.04 94.76(2.12,3.12)0.77 1.0 94.60(0.64,4.76)0.80 94.92(0.40,4.68)0.77 95.10(2.32,2.58)0.81 95.52(1.50,2.98)0.97 94.52(2.78,2.70)0.85 1.2 94.12(0.52,5.36)0.86 94.36(0.38,5.26)0.83 94.94(2.20,2.86)0.88 94.84(1.78,3.38)0.98 94.26(2.72,3.02)0.92
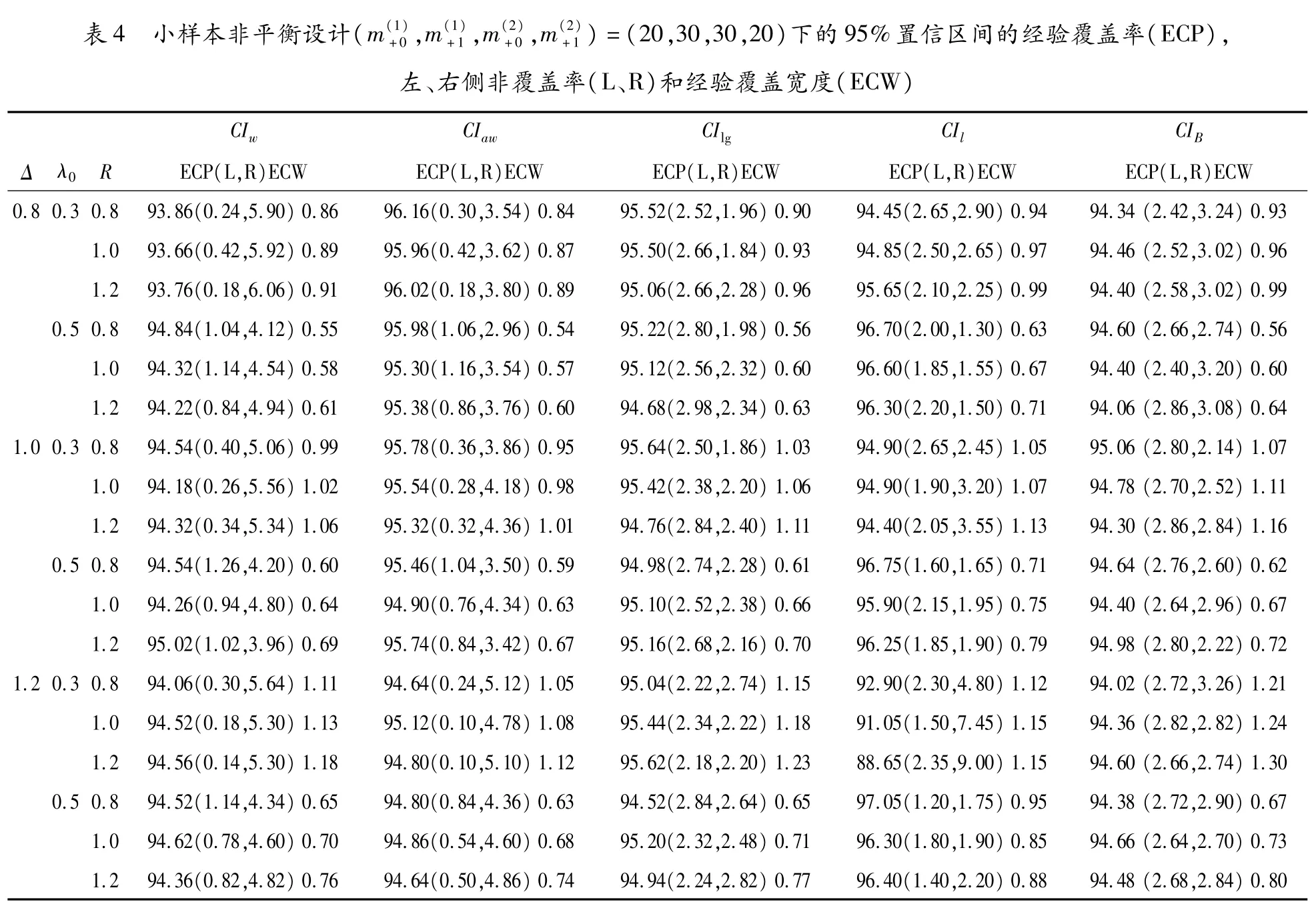
表4 小样本非平衡设计(m(1)+0,m(1)+1,m(2)+0,m(2)+1)=(20,30,30,20)下的95%置信区间的经验覆盖率(ECP),左、右侧非覆盖率(L、R)和经验覆盖宽度(ECW)CIw CIaw CI lg CIl CIB Δ λ0 R ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW 0.8 0.3 0.8 93.86(0.24,5.90)0.86 96.16(0.30,3.54)0.84 95.52(2.52,1.96)0.90 94.45(2.65,2.90)0.94 94.34(2.42,3.24)0.93 1.0 93.66(0.42,5.92)0.89 95.96(0.42,3.62)0.87 95.50(2.66,1.84)0.93 94.85(2.50,2.65)0.97 94.46(2.52,3.02)0.96 1.2 93.76(0.18,6.06)0.91 96.02(0.18,3.80)0.89 95.06(2.66,2.28)0.96 95.65(2.10,2.25)0.99 94.40(2.58,3.02)0.99 0.5 0.8 94.84(1.04,4.12)0.55 95.98(1.06,2.96)0.54 95.22(2.80,1.98)0.56 96.70(2.00,1.30)0.63 94.60(2.66,2.74)0.56 1.0 94.32(1.14,4.54)0.58 95.30(1.16,3.54)0.57 95.12(2.56,2.32)0.60 96.60(1.85,1.55)0.67 94.40(2.40,3.20)0.60 1.2 94.22(0.84,4.94)0.61 95.38(0.86,3.76)0.60 94.68(2.98,2.34)0.63 96.30(2.20,1.50)0.71 94.06(2.86,3.08)0.64 1.0 0.3 0.8 94.54(0.40,5.06)0.99 95.78(0.36,3.86)0.95 95.64(2.50,1.86)1.03 94.90(2.65,2.45)1.05 95.06(2.80,2.14)1.07 1.0 94.18(0.26,5.56)1.02 95.54(0.28,4.18)0.98 95.42(2.38,2.20)1.06 94.90(1.90,3.20)1.07 94.78(2.70,2.52)1.11 1.2 94.32(0.34,5.34)1.06 95.32(0.32,4.36)1.01 94.76(2.84,2.40)1.11 94.40(2.05,3.55)1.13 94.30(2.86,2.84)1.16 0.5 0.8 94.54(1.26,4.20)0.60 95.46(1.04,3.50)0.59 94.98(2.74,2.28)0.61 96.75(1.60,1.65)0.71 94.64(2.76,2.60)0.62 1.0 94.26(0.94,4.80)0.64 94.90(0.76,4.34)0.63 95.10(2.52,2.38)0.66 95.90(2.15,1.95)0.75 94.40(2.64,2.96)0.67 1.2 95.02(1.02,3.96)0.69 95.74(0.84,3.42)0.67 95.16(2.68,2.16)0.70 96.25(1.85,1.90)0.79 94.98(2.80,2.22)0.72 1.2 0.3 0.8 94.06(0.30,5.64)1.11 94.64(0.24,5.12)1.05 95.04(2.22,2.74)1.15 92.90(2.30,4.80)1.12 94.02(2.72,3.26)1.21 1.0 94.52(0.18,5.30)1.13 95.12(0.10,4.78)1.08 95.44(2.34,2.22)1.18 91.05(1.50,7.45)1.15 94.36(2.82,2.82)1.24 1.2 94.56(0.14,5.30)1.18 94.80(0.10,5.10)1.12 95.62(2.18,2.20)1.23 88.65(2.35,9.00)1.15 94.60(2.66,2.74)1.30 0.5 0.8 94.52(1.14,4.34)0.65 94.80(0.84,4.36)0.63 94.52(2.84,2.64)0.65 97.05(1.20,1.75)0.95 94.38(2.72,2.90)0.67 1.0 94.62(0.78,4.60)0.70 94.86(0.54,4.60)0.68 95.20(2.32,2.48)0.71 96.30(1.80,1.90)0.85 94.66(2.64,2.70)0.73 1.2 94.36(0.82,4.82)0.76 94.64(0.50,4.86)0.74 94.94(2.24,2.82)0.77 96.40(1.40,2.20)0.88 94.48(2.68,2.84)0.80
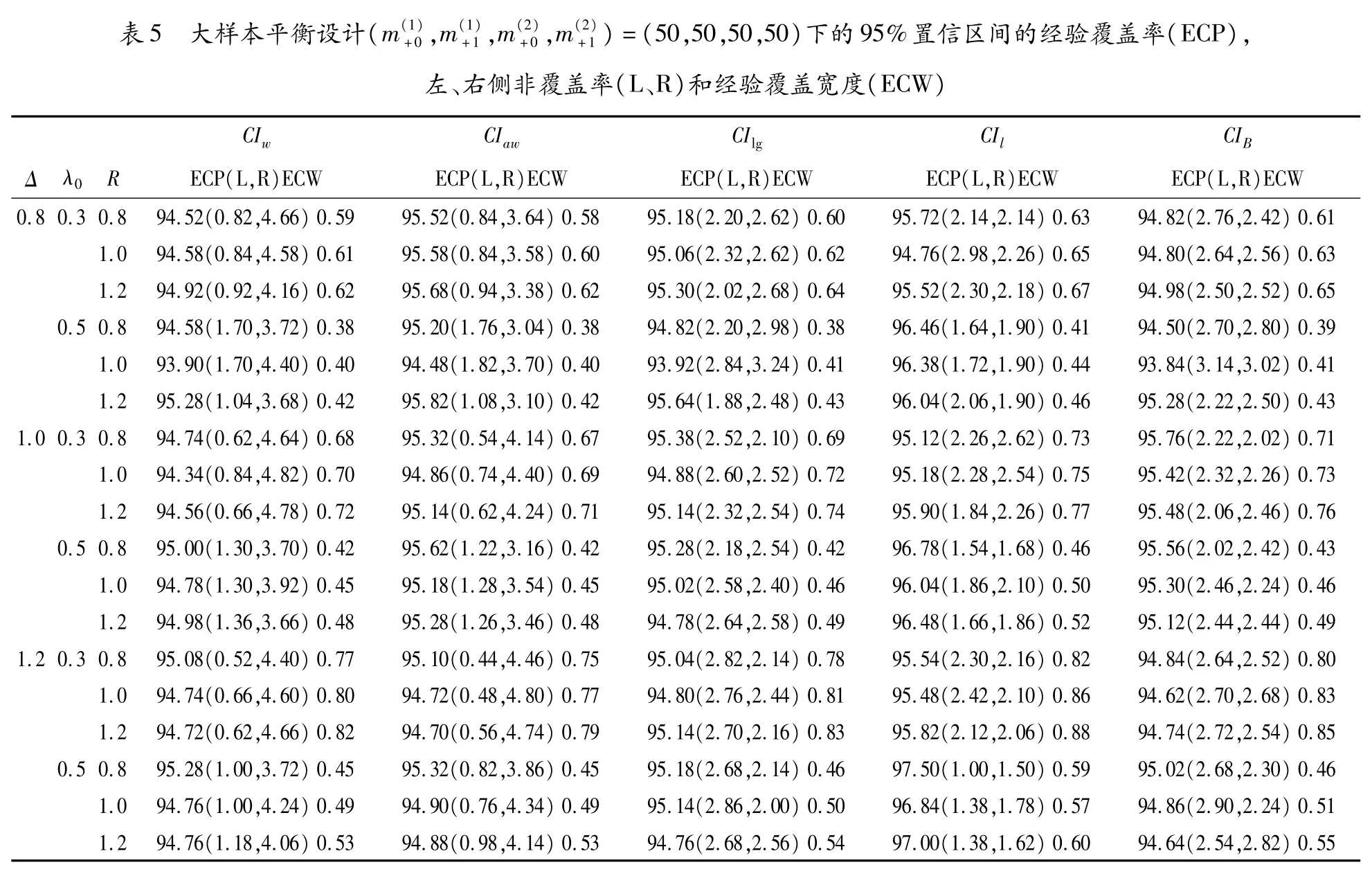
表5 大样本平衡设计(m(1)+0,m(1)+1,m(2)+0,m(2)+1)=(50,50,50,50)下的95%置信区间的经验覆盖率(ECP),左、右侧非覆盖率(L、R)和经验覆盖宽度(ECW)CIw CIaw CI lg CIl CI B Δ λ0 R ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW 0.8 0.3 0.8 94.52(0.82,4.66)0.59 95.52(0.84,3.64)0.58 95.18(2.20,2.62)0.60 95.72(2.14,2.14)0.63 94.82(2.76,2.42)0.61 1.0 94.58(0.84,4.58)0.61 95.58(0.84,3.58)0.60 95.06(2.32,2.62)0.62 94.76(2.98,2.26)0.65 94.80(2.64,2.56)0.63 1.2 94.92(0.92,4.16)0.62 95.68(0.94,3.38)0.62 95.30(2.02,2.68)0.64 95.52(2.30,2.18)0.67 94.98(2.50,2.52)0.65 0.5 0.8 94.58(1.70,3.72)0.38 95.20(1.76,3.04)0.38 94.82(2.20,2.98)0.38 96.46(1.64,1.90)0.41 94.50(2.70,2.80)0.39 1.0 93.90(1.70,4.40)0.40 94.48(1.82,3.70)0.40 93.92(2.84,3.24)0.41 96.38(1.72,1.90)0.44 93.84(3.14,3.02)0.41 1.2 95.28(1.04,3.68)0.42 95.82(1.08,3.10)0.42 95.64(1.88,2.48)0.43 96.04(2.06,1.90)0.46 95.28(2.22,2.50)0.43 1.0 0.3 0.8 94.74(0.62,4.64)0.68 95.32(0.54,4.14)0.67 95.38(2.52,2.10)0.69 95.12(2.26,2.62)0.73 95.76(2.22,2.02)0.71 1.0 94.34(0.84,4.82)0.70 94.86(0.74,4.40)0.69 94.88(2.60,2.52)0.72 95.18(2.28,2.54)0.75 95.42(2.32,2.26)0.73 1.2 94.56(0.66,4.78)0.72 95.14(0.62,4.24)0.71 95.14(2.32,2.54)0.74 95.90(1.84,2.26)0.77 95.48(2.06,2.46)0.76 0.5 0.8 95.00(1.30,3.70)0.42 95.62(1.22,3.16)0.42 95.28(2.18,2.54)0.42 96.78(1.54,1.68)0.46 95.56(2.02,2.42)0.43 1.0 94.78(1.30,3.92)0.45 95.18(1.28,3.54)0.45 95.02(2.58,2.40)0.46 96.04(1.86,2.10)0.50 95.30(2.46,2.24)0.46 1.2 94.98(1.36,3.66)0.48 95.28(1.26,3.46)0.48 94.78(2.64,2.58)0.49 96.48(1.66,1.86)0.52 95.12(2.44,2.44)0.49 1.2 0.3 0.8 95.08(0.52,4.40)0.77 95.10(0.44,4.46)0.75 95.04(2.82,2.14)0.78 95.54(2.30,2.16)0.82 94.84(2.64,2.52)0.80 1.0 94.74(0.66,4.60)0.80 94.72(0.48,4.80)0.77 94.80(2.76,2.44)0.81 95.48(2.42,2.10)0.86 94.62(2.70,2.68)0.83 1.2 94.72(0.62,4.66)0.82 94.70(0.56,4.74)0.79 95.14(2.70,2.16)0.83 95.82(2.12,2.06)0.88 94.74(2.72,2.54)0.85 0.5 0.8 95.28(1.00,3.72)0.45 95.32(0.82,3.86)0.45 95.18(2.68,2.14)0.46 97.50(1.00,1.50)0.59 95.02(2.68,2.30)0.46 1.0 94.76(1.00,4.24)0.49 94.90(0.76,4.34)0.49 95.14(2.86,2.00)0.50 96.84(1.38,1.78)0.57 94.86(2.90,2.24)0.51 1.2 94.76(1.18,4.06)0.53 94.88(0.98,4.14)0.53 94.76(2.68,2.56)0.54 97.00(1.38,1.62)0.60 94.64(2.54,2.82)0.55
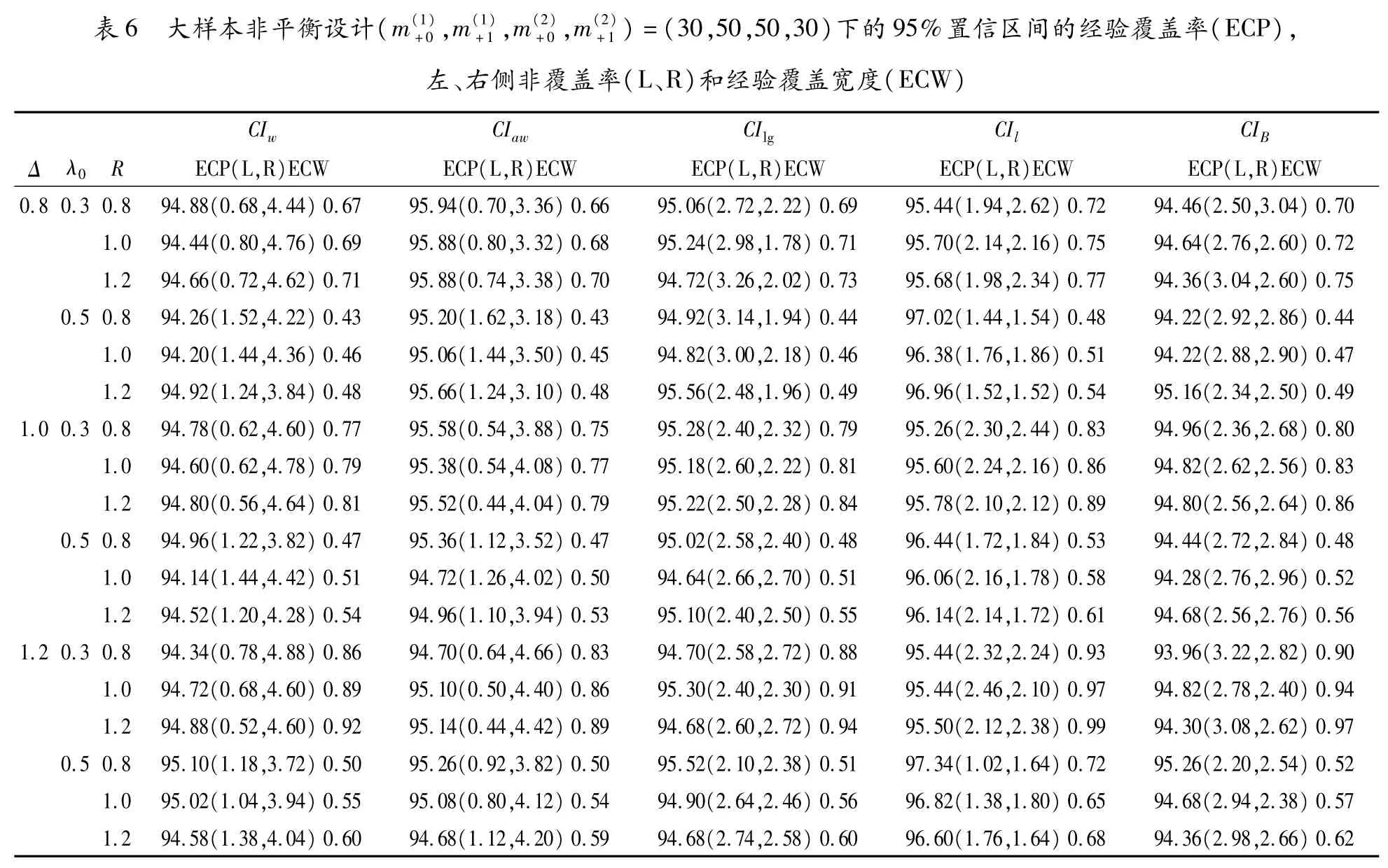
表6 大样本非平衡设计(m(1)+0,m(1)+1,m(2)+0,m(2)+1)=(30,50,50,30)下的95%置信区间的经验覆盖率(ECP),左、右侧非覆盖率(L、R)和经验覆盖宽度(ECW)CIw CIaw CI lg CIl CIB Δ λ0 R ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW ECP(L,R)ECW 0.8 0.3 0.8 94.88(0.68,4.44)0.67 95.94(0.70,3.36)0.66 95.06(2.72,2.22)0.69 95.44(1.94,2.62)0.72 94.46(2.50,3.04)0.70 1.0 94.44(0.80,4.76)0.69 95.88(0.80,3.32)0.68 95.24(2.98,1.78)0.71 95.70(2.14,2.16)0.75 94.64(2.76,2.60)0.72 1.2 94.66(0.72,4.62)0.71 95.88(0.74,3.38)0.70 94.72(3.26,2.02)0.73 95.68(1.98,2.34)0.77 94.36(3.04,2.60)0.75 0.5 0.8 94.26(1.52,4.22)0.43 95.20(1.62,3.18)0.43 94.92(3.14,1.94)0.44 97.02(1.44,1.54)0.48 94.22(2.92,2.86)0.44 1.0 94.20(1.44,4.36)0.46 95.06(1.44,3.50)0.45 94.82(3.00,2.18)0.46 96.38(1.76,1.86)0.51 94.22(2.88,2.90)0.47 1.2 94.92(1.24,3.84)0.48 95.66(1.24,3.10)0.48 95.56(2.48,1.96)0.49 96.96(1.52,1.52)0.54 95.16(2.34,2.50)0.49 1.0 0.3 0.8 94.78(0.62,4.60)0.77 95.58(0.54,3.88)0.75 95.28(2.40,2.32)0.79 95.26(2.30,2.44)0.83 94.96(2.36,2.68)0.80 1.0 94.60(0.62,4.78)0.79 95.38(0.54,4.08)0.77 95.18(2.60,2.22)0.81 95.60(2.24,2.16)0.86 94.82(2.62,2.56)0.83 1.2 94.80(0.56,4.64)0.81 95.52(0.44,4.04)0.79 95.22(2.50,2.28)0.84 95.78(2.10,2.12)0.89 94.80(2.56,2.64)0.86 0.5 0.8 94.96(1.22,3.82)0.47 95.36(1.12,3.52)0.47 95.02(2.58,2.40)0.48 96.44(1.72,1.84)0.53 94.44(2.72,2.84)0.48 1.0 94.14(1.44,4.42)0.51 94.72(1.26,4.02)0.50 94.64(2.66,2.70)0.51 96.06(2.16,1.78)0.58 94.28(2.76,2.96)0.52 1.2 94.52(1.20,4.28)0.54 94.96(1.10,3.94)0.53 95.10(2.40,2.50)0.55 96.14(2.14,1.72)0.61 94.68(2.56,2.76)0.56 1.2 0.3 0.8 94.34(0.78,4.88)0.86 94.70(0.64,4.66)0.83 94.70(2.58,2.72)0.88 95.44(2.32,2.24)0.93 93.96(3.22,2.82)0.90 1.0 94.72(0.68,4.60)0.89 95.10(0.50,4.40)0.86 95.30(2.40,2.30)0.91 95.44(2.46,2.10)0.97 94.82(2.78,2.40)0.94 1.2 94.88(0.52,4.60)0.92 95.14(0.44,4.42)0.89 94.68(2.60,2.72)0.94 95.50(2.12,2.38)0.99 94.30(3.08,2.62)0.97 0.5 0.8 95.10(1.18,3.72)0.50 95.26(0.92,3.82)0.50 95.52(2.10,2.38)0.51 97.34(1.02,1.64)0.72 95.26(2.20,2.54)0.52 1.0 95.02(1.04,3.94)0.55 95.08(0.80,4.12)0.54 94.90(2.64,2.46)0.56 96.82(1.38,1.80)0.65 94.68(2.94,2.38)0.57 1.2 94.58(1.38,4.04)0.60 94.68(1.12,4.20)0.59 94.68(2.74,2.58)0.60 96.60(1.76,1.64)0.68 94.36(2.98,2.66)0.62
2)正如预期,修正的Wald置信区间能够明显地改善Wald置信区间的统计性质,因为基于修正后的Wald统计量所构造的置信区间的经验覆盖率更接近预先给定的置信水平,区间宽度也更窄。
3)从各置信区间的左、右侧非覆盖率(LNCP、RNCP)的角度来看,在不同的样本量和参数组合下,CIlg和CIB的左、右侧非覆盖率LNCP、RNCP几乎相等,说明CIlg和CIB有良好的区间位置。
4 实例分析
针对引言中的儿童中耳炎临床数据,采用本文中提出的方法得到置信区间CIw、CIaw、CIlg、CIl和CIB分别为:[0.535 0,0.939 8]、[0.542 8,0.944 4]、[0.560 4,0.970 3]、[0.424 5,1.473 8]和[0.555 7,0.971 4],相应的区间宽度分别为:0.404 8,0.401 6,0.409 9,1.049 3,0.415 7。可以看到:CIaw区间宽度最短,而CIl的区间宽度最大,这与模拟结果一致。
5 结论
研究了单双边混合试验数据下2种药物的治愈率之比的区间估计问题,分别给出了基于Wald统计量、修正的Wald统计量和基于对数变换、似然比检验统计量的置信区间以及Bootstrap重抽样置信区间的构造方法。模拟研究表明:基于修正的Wald统计量,基于对数变换和Bootstrap重抽样置信区间(即CIaw、CIlg和CIB),即使在小样本下都有很好的覆盖性质。从区间位置的角度考察,基于对数变换和Bootstrap重抽样置信区间通常具有近似对称的左右非覆盖概率,具有良好的区间位置。

