一种基于汉明矩阵的运动链同构识别方法

赵 柯，许 辉，吴昌军，邓 涛

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆交通大学 航空学院，重庆 400074）

在机械结构设计过程中，同构运动链的识别既是重点也是难点［1-2］。为了解决这一问题，许多有效的方法被相继提出。

最早的同构识别主要依靠设计者的视觉观察，这种方法只适用于杆副数量较低的情况，且效率低，缺乏理论依据［3］。后来随着图论的发展和引入，运动链的同构问题得以简化，识别方法开始向系统化和理论化方向发展。按照识别原理的不同，这些方法大致可以分为以下几大类。特征多项式法［4-8］主要通过对比矩阵的特征多项式来判别同构，此类方法效率高，但部分方法已发现反例，尽管这些反例对于机械领域来说并没有实际意义。代码法［9-10］主要通过转化拓扑图为唯一的形式来获得判定同构的代码，此类方法具有较高的有效性且具有解码性，但当拓扑图的杆副数量较大或图形对称性较强时，其效率较低。路径［11］或距离法［12］主要利用其特定的概念来生成一些判定码，这类方法的有效性较高，但涉及的概念和参数较多，不便于计算机实现。人工神经网络法［13］为解决同构提供了新的方向，但方法的有效性尚须进一步验证。连杆连接数和平均信息量法［14］引入了信息论领域的概念，2个新的不变量被提出来检测同构，但其并不适用于复铰链。邻接矩阵幂序列法［15-16］依赖于邻接矩阵的幂来判定同构，但后者［16］在判别机构倒置的某些情况下已经出现失效。汉明数串法［17］是一种将汉明矩阵简化表示为数字串来识别同构的方法。此方法效率高，计算简单，但汉明数串非常长，特别是在大型运动链的情况下。此外，如果一阶汉明数串失败，则需要二阶汉明数串，这使得过程变得更加复杂。分裂汉明数串（SHS）法［18］是将汉明数串划分为3部分以判定含有移动副的运动链。

机械结构创新设计迫切需要一种简单、高效和可靠的同构筛选方法。上述大多数方法都涉及抽象的概念和复杂的中间参数比较，且随着杆副数量增大，一些方法的效率和有效性会大大降低。因此，本文基于汉明矩阵提出了一种新的同构识别方法，即从汉明矩阵的平方阵中导出同构识别码识别同构运动链。若两拓扑图的同构识别码相同，则它们是同构的，否则是非同构的。此方法简单、高效且整个判定过程在计算机上极易实现。

1 运动链拓扑图的矩阵描述

1.1 运动链拓扑图的连杆邻接矩阵

对于运动链来说，将其杆件表示为顶点，运动副表示为边，便转化成了其对应的运动链拓扑图［19］，瓦特链及其拓扑图如图1所示。运动链拓扑图的连杆邻接矩阵A是其最基础的矩阵，大多数同构识别方法都以它为已知量。其元素aij为：

其中，i和j为连杆标号或顶点标号，i和j为从1到n的整数，n为运动链的连杆数。图1所示的瓦特链连杆邻接矩阵如下：

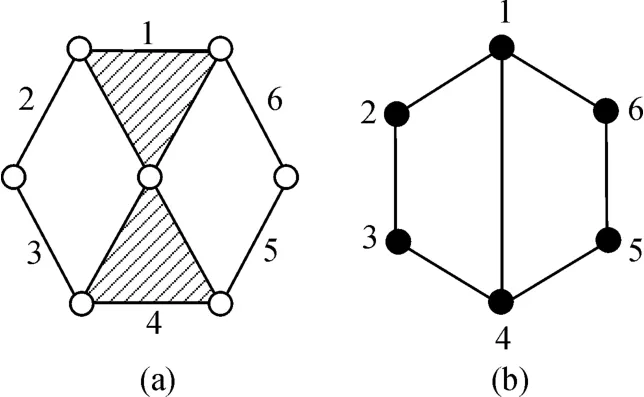
图1 瓦特链及其拓扑图

1.2 运动链拓扑图的汉明矩阵

连杆邻接矩阵的每一行代表了该标号的连杆是否与其他标号的连杆直接连接。但运动链中的间接连接等其他信息并未直观地表现在连杆邻接矩阵中。两连杆之间的连接信息需要更深入地挖掘以提高识别方法的辨别能力。因此数字通信领域的汉明技术被引入以生成连杆汉明矩阵H，它的元素hij表示了连杆i和连杆j各自连接关系的不同程度［17］。以连杆邻接矩阵为已知，hij定义为连杆邻接矩阵的第i行和第j行所有列中不同元素的总和，数学表达如式（2）和式（3）所示。

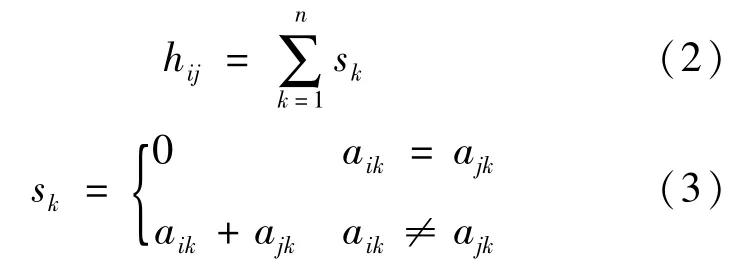
例如，对于上述瓦特链连杆邻接矩阵中的第1行和第2行来说，其第1、2、3、4、6列的元素都不同，故h12＝1+1+1+1+1＝5。同理可得图1的汉明矩阵，如下所示：

2 识别码的获得流程与同构识别

2.1 识别码获得流程

以连杆邻接矩阵为已知量的同构识别码获得流程如图2所示。

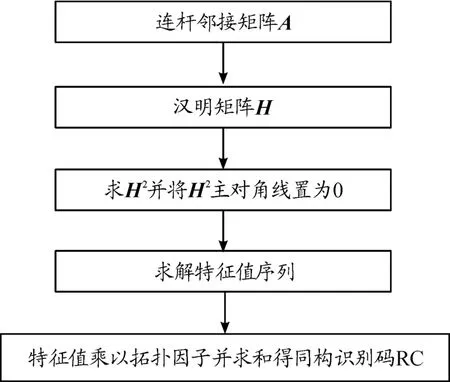
图2 同构识别码流程框图

步骤1：导出汉明矩阵。根据式（2）和式（3）从连杆邻接矩阵中获得汉明矩阵。

步骤2：求汉明矩阵的平方得平方阵H2，并将平方阵H2的主对角线元素置为0。一方面，由于以汉明矩阵为判定依据的一阶汉明数串在10杆链中已经失效，这证明汉明矩阵中包含的信息量仍旧不足。于是本文求得汉明矩阵平方以获得更多的细节特征，并以此为基础，利用后续步骤进一步挖掘深层次的拓扑特性。另一方面，之所以将主对角线元素置为0，主要是为了排除对角线元素对特征值的影响，因为存在于运动链中的连杆不能与自身相连接。

步骤3：求解主对角线元素为0的平方阵H2的特征值λ1，…，λn，并将特征值按从小到大的顺序排列得特征值序列。对特征值排序的目的是消除因特征值顺序不同而产生的不同识别码值和进一步导致的误判。如图1的特征值序列为：-78.027 969 292 722 6，-76.115 844 782 509 9，-58.000 000 000 000 0，-58.000 000 000 000 0，62.115 844 782 509 9，208.027 969 292 723。

步骤4：将上述的特征值λ乘以拓扑因子k，并将所得的乘积求和以获得最终的同构识别码RC（recognition code）。此处的拓扑因子k定义为从1到n的整数，此步骤如式（4）所示。拓扑因子k的作用是解决两图因特征值不同而总和相同导致的误判。如：1、2、3与1、1、4的和都为6，如果以此为判定依据，那么它们是同构。但事实上它们的组成情况却是不同的，即异构。若将其乘以拓扑因子前者为14，后者为15，则可以判定它们为异构。如图1的识别码RC＝922.487 380 811 142 7。

2.2 运动链同构的识别

由于运动链连杆的标号是任意的，不同的标号会得到不同的运动链，但这些运动链拥有相同的杆副连接特征，所以它们被称为同构运动链，其对应的拓扑图被称为同构拓扑图。本文提出的RC是一个运动链拓扑图的不变量，它不随着连杆标号的改变而改变。因此RC可以作为同构判定的依据。若已知两条链是同构，那么它们的识别码RC应相等，反之亦然。

3 判定实例

3.1 10杆运动链

图3为一阶汉明数串误判为同构的两10杆1自由度异构运动链［17］。

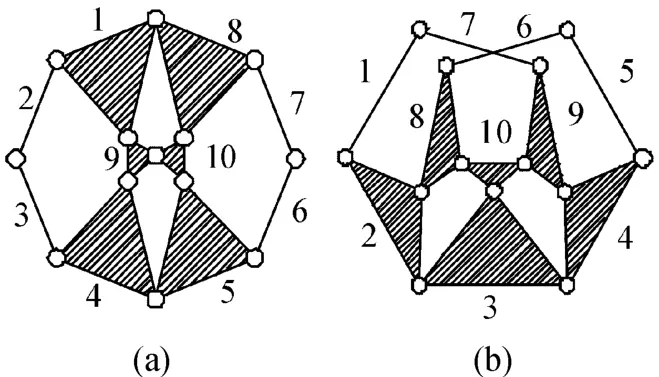
图3 两10杆异构运动链示意图

两链的汉明矩阵如下：

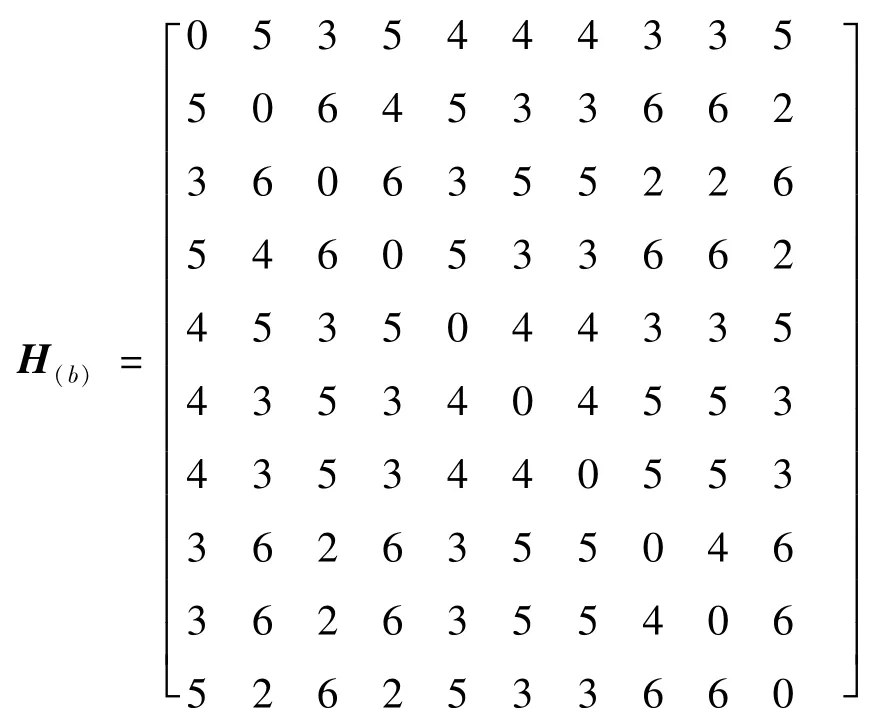
由上可知，两矩阵的行和元素组成情况存在着一一对应关系，这直接导致了一阶汉明数被判定为同构。由前文可得两链的同构识别码，如表1所示。

表1 图3两运动链的同构识别码RC

显然表1的两RC不相等，因此图3中的两运动链为异构链。

3.2 15杆等谱拓扑图

图4中的两运动链为众多特征向量法的判别反例。由于其结构的冗余，尽管它们在机械领域中并没实用价值，但众多学者仍旧热衷于判定此图，并将其作为检验各种判定方法的常用实例，本文也不例外。图4的特殊性在于其连杆邻接矩阵的特征值相同即等谱，这是导致误判为同构的重要原因。另外，一些方法即使能够正确判定这一实例，但却需要很大的计算量［20］。

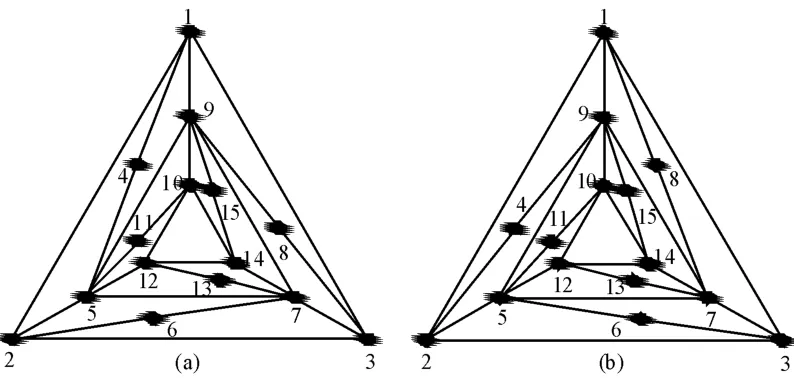
图4 两15杆异构运动链拓扑图

通过图2的流程可得两运动链拓扑图的同构识别码RC，并将其列于表2中。

显然表2的两RC不相等，因此图4中的两拓扑图为异构图。另外，值得一提的是此两RC的计算量并不大。

表2 图4两拓扑图的同构识别码RC

3.3 28杆运动链拓扑图

图5来自于参考文献［21］。已知图5（a）和（b）仅是顶点标号不同，（c）为（a）移动一条边后所得的图形，所以（a）和（b）为同构，（a）和（c）为异构。计算可得三拓扑图的同构识别码RC如表3所示。

图5 三28杆运动链拓扑图

由表3可知，图5（a）与（b）的RC相等，即它们为同构拓扑图；图5（a）与（c）的RC不相等，即它们为异构拓扑图。此结果与参考文献一致。

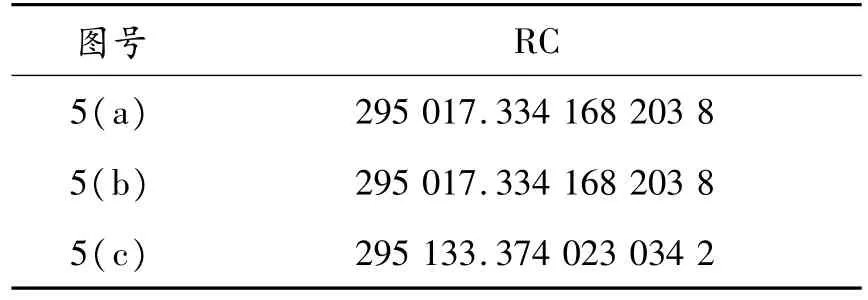
表3 图5三拓扑图的同构识别码RC

4 结论

1）本判别方法创造性地对汉明矩阵进行平方运算以获得运动链的更多连接细节，并将平方阵主对角线元素置为0，排除其对后续特征值的影响。此外，本文定义了拓扑因子，并将拓扑因子与特征值的乘积求和得到运动链的不变量，即运动链同构识别码RC。

2）本方法逻辑简单易理解，开发本方法的计算机程序非常容易，即使对于仅有编程基础的人员也容易掌握。另外在计算机程序的帮助下，只需输入连杆邻接矩阵即可实现自动识别，判别过程简单、高效、准确。

3）对于其他方法失效的实例，本方法也能够成功识别。此外，在研究阶段，本方法的有效性经过了大量的实例验证，由于篇幅限制，并未将其列入此文中。

4）本方法易推广到其他类型运动链的同构识别中，如复铰链、齿轮链，只需简单地修改连杆邻接矩阵的元素，识别方法无需修改。

5）本方法对于连杆数高于28的运动链的有效性尚须进一步验证，另外本方法也不具有解码性。