基于断面经济优化设计的城市河道治理研究

王 松

(海城市水利事务服务中心，辽宁 海城 114200)

随着传统的工程水利向现代的环境、资源水利的转变，侧重于防洪排涝、引水抗旱要求的城市河流治理理念，逐渐转向人文化、景观化、生态化等多功能治理要求[1-4]。目前，对城市河流治理的国内外相关研究，比较集中于技术应用、景观理论及河道生态等方面，主要涉及河流治理后评价、水生态修复技术、河道功能治理体系、景观设计方法、河流健康评价指标、生态河道理论框架等。实践表明，对于任何河流的功能建设，河道治理都存在回收周期长、投资规模大的特征[5-6]。所以，在确保河流功能的情况下，如何使治理收益达到最大或最大程度的降低建设成本，已成为城市河道治理的重要研究课题。对此，通过优化设计城市河道断面，本研究提出治理方案优选模型，在满足生态景观功能的条件下实现治理效益的最大化。

1 河道治理的数学描述

从空间角度上，河道空间因治理工程的实施而发生改变。因此，可以从纵向、垂向和横向上构造河道空间位置函数，即：Ω=F(X，Z，Y)，从纵向河道中心线、坡地及横断面的角度整治城市河道。为维持河流的自然属性，整治工程通常不改变河道的中心线。所以，可利用坡降与河道断面的函数描述河道治理收益及成本。设定目标函数为最大化的治理收益，其数学表达式为：

maxY(X)=B(X)-C(X)

(1)

式中：X={φm，im-1}；H(X)∈Hr、E(X)∈Er、L(X)∈Lr、P(X)∈Pr。M为决策变量；im-1为m-1与m断面间的坡降；φm为m断面变量；Y(X)、B(X)、C(X)代表河道治理收益、效益和成本；H(X)、E(X)、L(X)、P(X)代表水利、生态、景观、用地规划的约束指标函数；Hr、Er、Lr、Pr水力、生态、景观、用地规划约束。

设断面m整治后的决策变量与河道原断面特征点为(xmn，zmn)、(xmn′，zmn′)，下一断面与断面m的距离为Lm。考虑规划用地指标约束、生态景观指标约束、水位约束、边坡约束、断面自身约束、堤岸及底坡衔接约束、河道收缩加高扩宽扩深约束作为优化模型的约束条件，具体如下：

1)考虑河宽等参数控制规划用地指标约束。

2)采用流速及断面型式等参数控制生态景观指标约束。

3)设hm、f为断面m水位和河道安全超高，利用公式hm+f≤zm1，zm0控制水位约束。

4)设mmin、mmax、ms边坡允许最小值、最大值和河道两侧边坡，并且ms的计算要考虑具体的断面形式，利用公式mmin≤ms≤mmax控制边坡约束。

5)采用公式xmn-1≤xmm、zmn≤zm1、zmn≤zm0控制断面自身约束，其中n=1，2，3……。

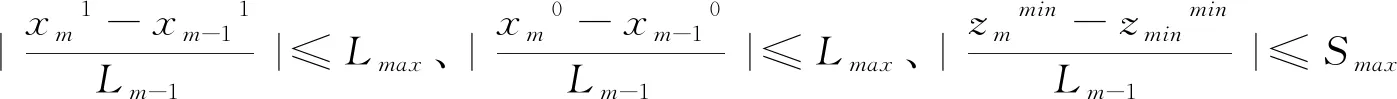
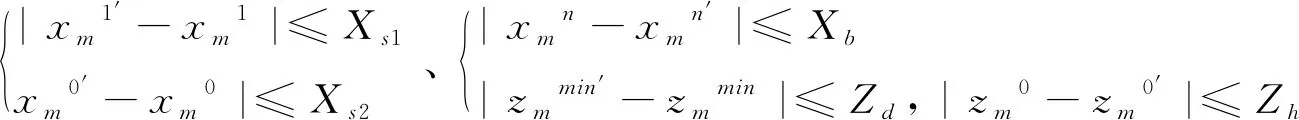
2 断面经济优化设计

2.1 实现流程

依据实际情况具体概化所构建的模型，从而解决模型约束条件多、变量多的问题，概化流程如图1所示。

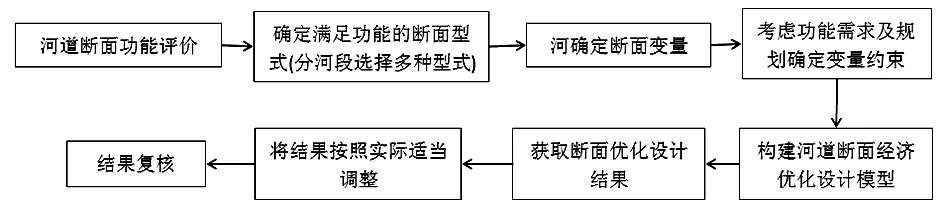
图1 河道断面经济优化设计

2.2 断面型式具体化

为满足城镇河道的亲水性、生态性、景观性等要求通常选用复式断面，复式断面可以消除视觉景观欣赏受水位高低变化的影响，满足枯水位、常水位、洪水位等不同水位变化波动的亲水性要求。将多层亲水平台与复式断面相结合，可以满足自然亲水性和河道航运、防洪排涝等要求，并确保河流在枯水期拥有适宜宽度的景观水面。针对四季水位存在较大变化的北方城市河道，其普遍适用且效果理想的断面类型为复式断面。因此，确定断面型式随即也确定了相应的决策变量。

2.3 约束条件的概化

根据规范要求和相关经验成果完成河道设计，通过对河道型式的简化设计，明确变量、简化约束，并对变量范围进一步细化。确定断面型式后其自身断面约束自动满足，而规划用地范围约束、堤岸及底坡衔接约束、收缩加高扩宽扩深约束等按照河道断面特征高程和特征宽度确定。根据经验设定统一坡降或者整治后河道坡降范围，从而达到底坡衔接要求。各个断面的水位要符合不超过路面要求和堤顶超高要求，水流速度符合不冲刷流速允许要求。

2.4 目标函数的概化

优化模型只分析因断面变化，而引起的河道治理成本与工程效益的改变量。效益计算不考虑工程实施后周围直接经营性收益、附近地产增值效益、生态环境效益，仅考虑因河道滩地收缩而节约出来的土地效益，若河段或河道滩地不能收缩则不考虑此项，单位面积上平面方向的土地效益用B1衡量。考虑以下因素确定治理成本：①挖方成本，设断面j的扩挖面积和单位体积的挖方成本为S1j、C1；②填方成本，设断面j的填方面积和单位体积的填方成本为S2j、C2；③建堤成本，设断面j的加堤面积和重新加堤改变断面的成本为S3j、C3；④边坡整治成本，设两端面之间边坡的面积和单位面积上河道纵剖面方向的边坡整治成本为S4j、C4，断面j与下断面间的距离及其与河岸收缩距离为Lj、Wj。综合考虑各因素条件，确定河道整治成本C，即：

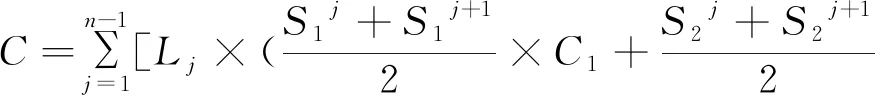
(2)

土地效益B的表达式为：

(3)

根据以上运算结果计算综合收益Y，即：

Y=B-C

(4)

3 实例应用

海城市某河道治理段长11.2km，下游闸控设计流量380m3/s。依据评估结果和现场调查资料，河道过流能力无法达到设计要求，有必要考虑河道景观、通航、防洪排涝等功能实施景观治理[7-8]。经充分论证，拟选择多级复式断面进行城市河道整治，该断面型式的决策变量为φm=(b,d,e,f,z,z1,z2,m1,m2)，其中m1、m2为复式梯形断面上坡段、下坡段坡度；z、z1、z2为河道断面的底高程、一级平台高程和顶高程；b、f为河道断面底宽和复式梯形断面二级平台宽度；d、e为复式断面的一级平台宽度和一、二级平台垂直距离，断面尺寸如图2所示。

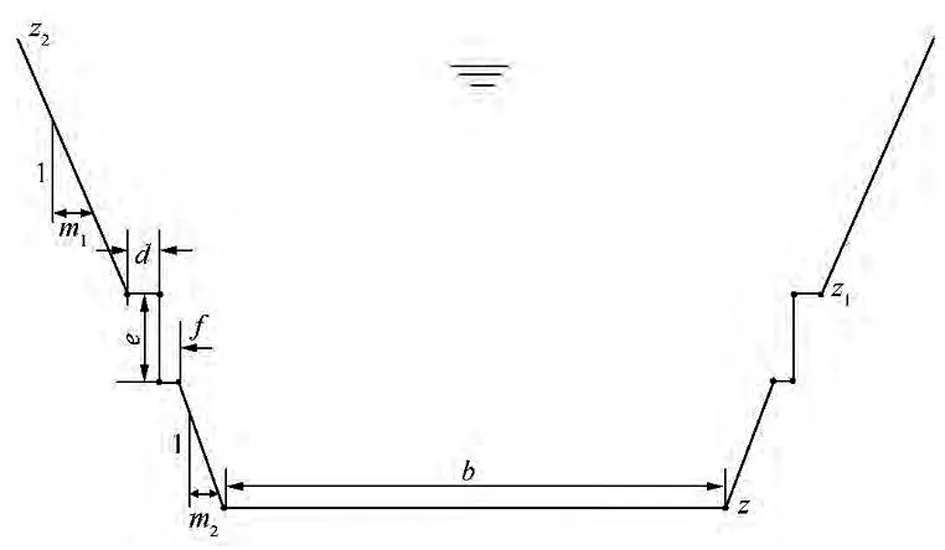
图2 河道复式断面

根据北方河道洪水位、常水位及枯水位存在较大高差的实际情况，设计多级复式断面以营造良好的亲水效果。将亲水平台设置在略高于枯水位和常水位处，其中一级平台高程z1的设定要考虑通航要求水位及常水位，平台宽度d和f的设定要结合用地情况以及景观绿化需求。依据特殊的造景要求(如景墙)和用地局促条件，设定两平台间的挡墙形式为直立型，并考虑航道要求的标准水深设定挡墙之间距离e。结合用地约束以及景观布置要求，对边坡坡度进行合理的设定。由此，可以确定参数m1、m2、d、e、f、z1的取值，依次为3.0m、2.5m、3.0m、1.2m、2.0m和2.8m。

3.1 约束条件

综合考虑以下要求确定约束条件：①河道可扩宽与收缩范围利用规划用地需求确定，并依据b来控制约束；②根据每个断面的z、z2确定堤岸及堤坡衔接约束、加高扩深约束；③整治后河道底坡范围按照经验合理设定，并达到堤坡衔接要求，该河道整治工程设定统一底坡i，其取值区间为0.000 02-0.000 2，各个断面底高程按照下游断面底高程和设定的河道坡降确定；④各断面水位符合不超过路面和堤顶超高的要求，其水流速度符合不冲刷流速所允许的要求。

3.2 决策变量

河道整治复式断面型式如图2，若确定过流流量、底高程z、底宽b和断面水位，即可计算两端面平均水力坡度、水力半径和断面过流面积。依据确定的下游河道闸控水位，在恒定流(380m3/s)的设计流量下，利用确定的底坡i和逐段试算法求出各断面水位。设安全超高加上水位等于堤顶高程z2，通过分析合理设计安全超高1.2m，明确水位后可随之计算堤顶高程。河道整治设定统一坡降，则底坡i、最下游断面的底高程z以及各个断面的底宽b为整条河道的决策变量。根据下游与河道衔接的实际，以原河道下游断面底高程作为整治河道下游断面底高程z。因此，采取的统一底坡i以及各个断面的底宽b为整个河道的治理断面变量。通过评估河道断面功能，将整治河段划分为10个断面，则底坡i以及10个断面底宽b为所有的决策变量。

3.3 目标函数

设定收益Y=B-C为目标函数，其中B、C为河道整治效益与成本。依据公式(2)-(4)，b1j、b0j为收缩断面和原断面堤顶宽度，设C1、C2、C3、C4取4.25元、16.8元、20元、20元，土地效益B1取600元。

3.4 优化结果

将目标函数运用遗传算法加以优化，其实现流程如图3所示。为实现河道整治的最大化收益，设定底坡i值0.000 05，该条件下整治工程取得的收益为1.26亿元，优化结果见表1。

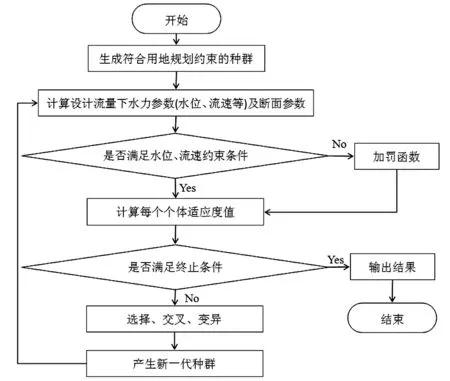
图3 目标函数的优化

表1 河道整治优化设计

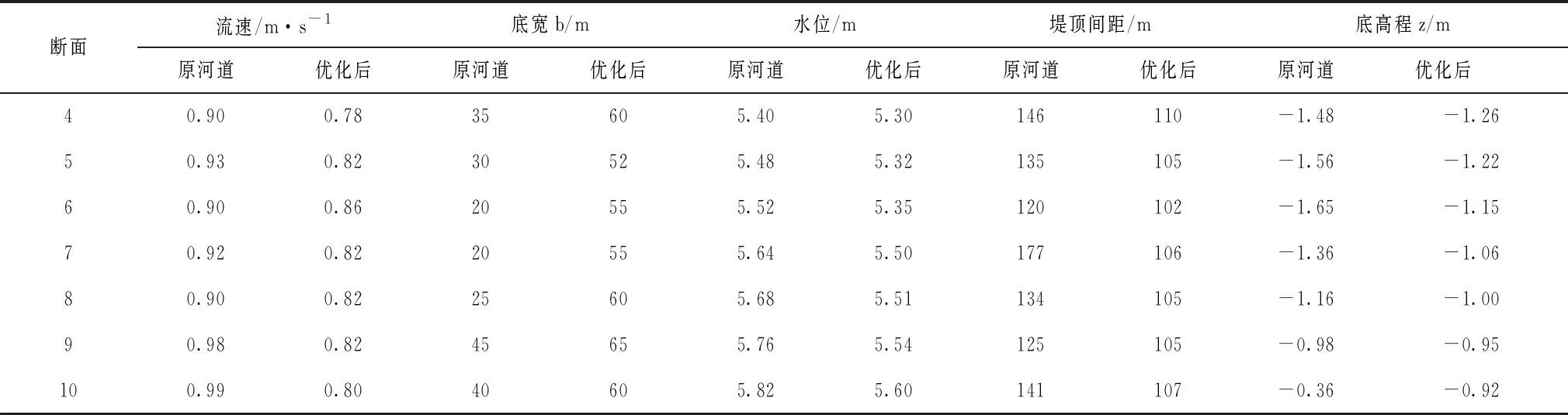
续表1 河道整治优化设计

通过对比分析某整治方案河道、优化设计河道以及原河道设计流量下的流速、水位、底高程，确定优化后的河道不仅能够大大降低洪水位，而且可以实现最大化河道治理收益[9-10]，如图4所示。相对而言，优化设计在一定程度上收缩了河道岸线，在不影响防洪安全的情况下节约了一定的土地，为城市发展提供更好的服务。与某整治方案相比，设计流量下优化方案的最高洪水位有所减少，断面平均流速波动范围较小，流态较为稳定，流速低于0.86m3/s，较某整治方案以及原方案具有更优的流速。

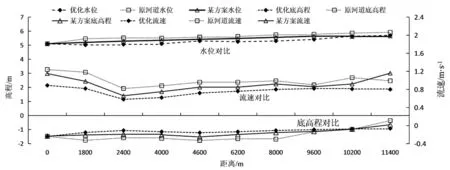
图4 对比分析图

4 结 论

城市河道综合治理对促进水生态文明建设发挥着巨大作用，有利于改善人居环境、维持生态系统平衡和优化人文景观。文章综合考虑城市河道治理约束条件多、投资规模大的特点，通过断面设计提出符合多功能要求的优化模型，并以实际验证了模型的可行性，可为设计经济可行性河道整治方案提供科学指导。