河道综合治理堤防承载能力的原位观测试验研究

孙 健

(辽宁天阳工程技术咨询服务有限公司，沈阳 110003)

1 概 述

河道综合治理需要对其堤防的承载能力进行设计，这其中其地质参数是其设计的重要指标[1]。当前对于河道堤防承载力的分析主要采用两种方式，第一种方式是采用室内试验，通过对治理河段的土层进行采样后，在室内完成其堤防承载能力相关参数的测定[2-6]。这种方式得到的参数结果较为准确，但需要消耗较长的时间，且受到采样方式的影响，其参数测定结果代表性存在不高的局限[7].第二种方式主要采用有限元计算的方式，这种方式在国内一些流域河道综合治理项目中得到实践，其一般用于大型河道，可通过有限元模型对不同地质参数进行模拟演算，并结合试验测定数据对其模型计算精度进行验证，这种方式在于可以模拟不同地质参数，代表性较好，适用于大型河道堤防承载力的计算，但由于模型参数较多，操作难度较大，适合于大型河道的地质参数计算，而对于一些中小河流而言，这种方式存在一定的局限性。近些年来，原位观测方式在一些水利工程建设地质参数测定中得到应用，但是对于河道综合治理中还应有较少，为此文章结合原位观测方式，结合河道综合治理工程实例，探讨和摸索该方式在河道综合治理堤防承载力的适用性，研究成果可为道综合治理稳定性参数设计提高重要参考。

2 试验原理

所谓原位观测即为在现场不扰动河道堤防土层的前提下，进行各项河道堤防各项地质参数的测定，从而对不同堤防承载力相关的设计参数进行获取。试验在地表荷载作用下，结合弹性力学对地表荷载力下的各相关参数进行测定，一般采用静力荷载的方式进行表层荷载试验，一般试验分为剪切、渗透、固结以及相对密度测定，各试验测定具有原理为：

采用垂直抨击方式进行静力荷载分析，垂向抨击原点坐标为o，地质土层中任何一个抨击点三维坐标为N(r,θ,z)，其与抨击原点o的直线距离为R，抨击点与原点o的直线夹角为β，则任意转角θ的应力测定值为：

(1)

式中：k为土层的应力参数值。

原位观测方式对堤防沉降分析主要采用函数拟合的方式进行反向应力计算，计算中一直保持相同的静力荷载：

(2)

式中：P为堤防沉降荷载，kPa；x为抨击的垂线距离，m。

通过对河道堤防应力和沉降原位观测试验基础上，对沉降荷载和应力荷载建立相关方程，对于圆形剖面土层，其方程为：

(3)

对于方形剖面土层，其方程为：

(4)

式中：v为泊松系数；E为静力荷载测定的河道堤防变形量，mm；D和B为圆形剖面直径，m和剖面宽度，m。

在进行土层变形量测定的基础上，对其承载力进行测定，测定方程为：

fspk=mfpk+(1-m)fsk

(5)

式中：fspk为堤防承载力测定值，kPa；fpk为土层剖面承载力测定值，kPa；fsk为不同参数测定条件下的堤防承载力测定值，kPa。

3 实例探讨

3.1 堤防概况

以某河道堤防治理为实例，探讨其河道堤防承载力原位观测试验的试验用，该河段土层主要为卵石和素填土，设计堤防梯形剖面，见图1，河道剖面总长度为3.94m，剖面高度为1m，主要为梯形剖面。

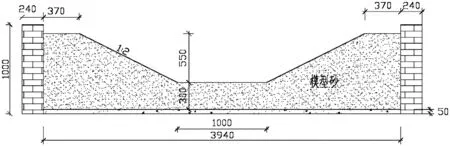
图1 设计堤防梯形剖面

3.2 物理参数测定

通过垂向抨击试验对不同土层的含水量、干湿密度、饱和密度、土壤容重、渗透孔隙比、渗透系数进行了分组试验，抨击试验测定参数，见表1；各土层地质参数测定结果，见表2。

表1 抨击试验测定参数

表2 各土层地质参数测定结果

续表2 各土层地质参数测定结果

采用重力垂直抨击试验时，需要确定最为适应的抨击次数，通过抨击组数分析其各抨击试验下的变异系数的变化区间，当变异系数较小时，一般认为达到最佳抨击次数，此时的可以对其土层的物理参数进行测定。从表1中可看出，当抨击次数位于42-49次时，其变异系数变化范围在0.2-0.3之间，变化幅度相对稳定，因此当试验组数达到49次时，其值较为稳定，修正系数为1.1，卵石层的建议抨击值要高于素填土。从不同地层物理参数可看出，堤身段其渗透系数总体变化较小，而砂砾段地层的渗透系数变化较大，变化幅度在4.0×102之间。砂砾段明显高于其堤身段地层的渗透系数。从不同地层的含水量建议值可看出，堤防剖面含水层的分布总体较为均匀，其干湿密度也较为接近，表明土层厚度以及土层类型对其含水层以及干湿密度垂向影响较小。堤身段孔隙比要高于砂砾孔隙比，主要因为其堤身段素填土较为稀疏，且位于上部，使得其具有相对较大孔隙比。

3.3 应力测定结果

在采用垂向抨击试验获取各土层物理指标后，分别进行剪切应力和沉降原位观测试验，不同剪切应力参数测定结果，见表3；不同剪切应力沉降参数测定结果，见表4。

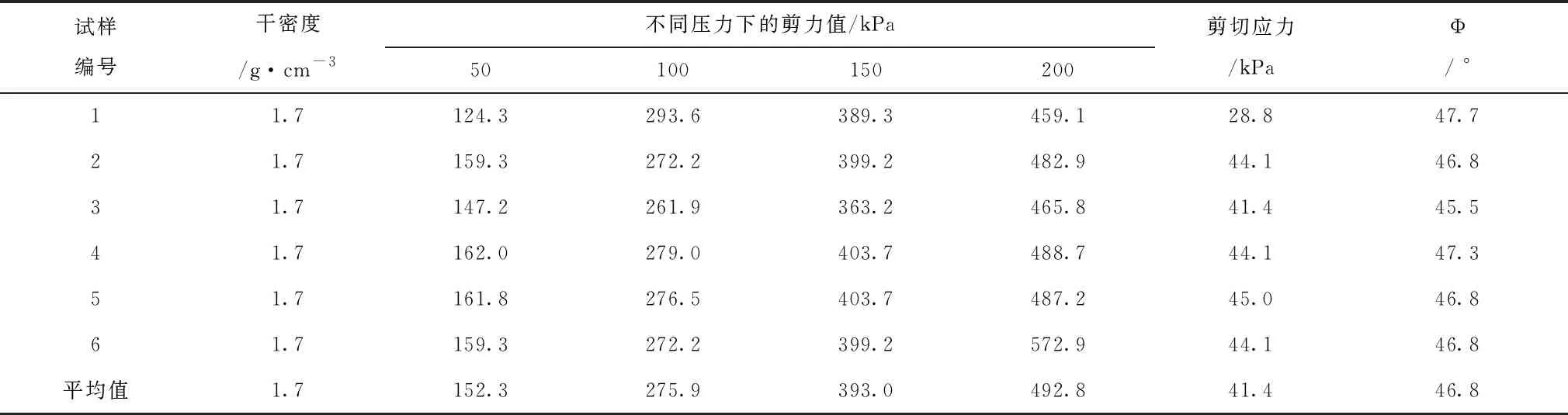
表3 不同剪切应力参数测定结果

表4 不同剪切应力沉降参数测定结果

从剪切应力试验结果可看出，随着静力荷载的增加，其压力参数逐步提高，但当静力荷载为150kPa时，其不同干密度条件下其剪切应力逐步趋于稳定变化，这主要是因为随着静力荷载的作用下，其土层将不断被压实，压实后的土层其剪切压力也将不再发生变化。试验河段剪切应力均值为41.4KPa，其不同剪切应力下的内摩擦角的均值为46.8°。从各试验河段堤防的沉降试验分析结果可看出，随着静力荷载的增加其压缩系数先减后增，这主要是当静力荷载增加时，由于先增加了其孔隙比，使得其沉降的压缩系数有所减少，当孔隙比增加到一定程度后，压缩系数逐步加大，并趋于稳定变化。

3.4 堤防承载力测定结果

在应力和沉降静力荷载试验分析的基础上，对各试验河段不同静力荷载条件下的堤防承载力进行综合测定，不同原位观测点静力荷载条件下堤防承载力测定结果，见表5。

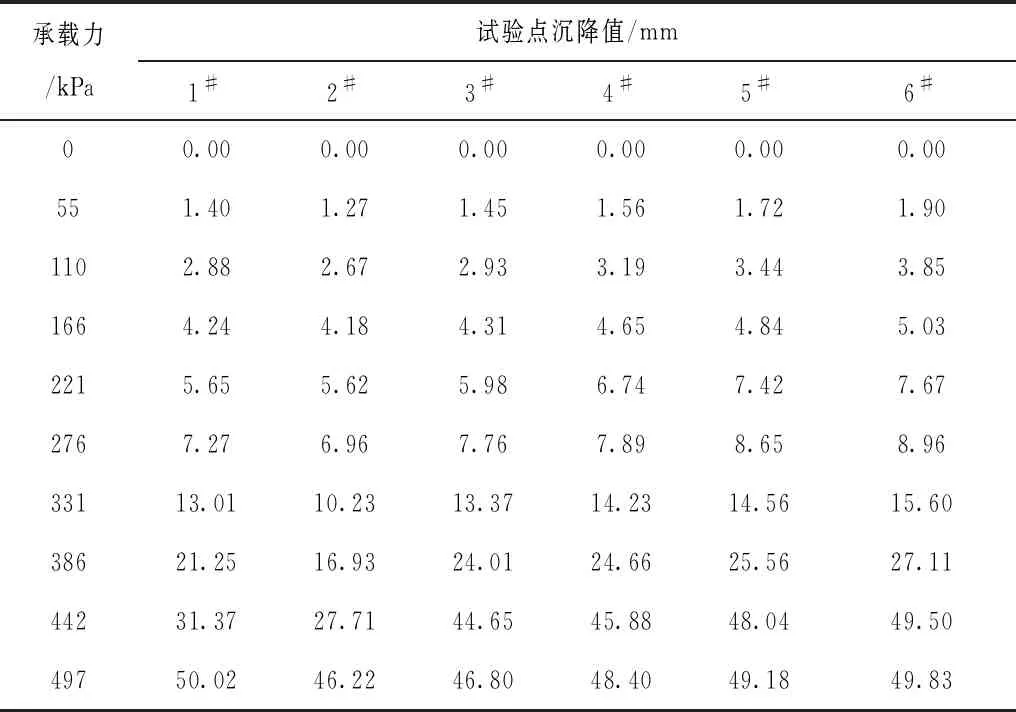
表5 不同原位观测点静力荷载条件下堤防承载力测定结果

从各原位观测点静力荷载下的承载力测定结果可看出，不用原位观测点下其承载力变化不同，且影响的沉降值有所差异，第1个原位观测点其沉降变化幅度最大，最大沉降和最低沉降之间的差值为48.62mm，沉降变化最小的为3#原位观测点，其最大沉降和最低沉降之间差值为45.35mm，不同原位观测点沉降差异值主要受其承载力的综合影响。随着承载力的提高，其沉降值逐步减小。除受到不同河段堤防承载力影响外，其剖面的剪切应力也是其沉降的重要影响因素，随着剪切应力的加大，各原位观测点的沉降也有所减小。

3.4 原位观测质量控制措施

原位观测试验的优点在于可不对堤防土层进行人为扰动的条件下进行其堤防承载能力各项指标的测定，且可以对不同堤防段的土层进行原位测定，代表性较高，其缺点在于需要较多的人力和物力试验观测，因此不适合于大型河道的堤防承载力的试验测定，在进行原位过程观测试验时，需要对以下几个方面进行质量控制，可提高原位观测指标测定的精度：

1)在进行观测试验时需要对不同土层进行多组试验，而不能采用单一组别试验对河道堤防不同土层的承载力指标进行测定。

2)在进行较大河流堤防承载力原位观测试验时，还需要对土层的残余强度进行原位测定，从而综合判定其堤防的承载能力。

3)在进行河道堤防承载力设计值选取时，应对其不同观测点沉降位移和静载的相关性进行分析，从而对其压力经验值进行合理设计。

4)在进行土层动力学指标测定时，不同土层的测定距离应尽量在1-1.5m范围内进行测定，对于复杂土层还应采用孔斜测量方式进行土样的测定。

4 结 论

1)原位观测试验的优点在于可不对堤防土层进行人为扰动的条件下进行其堤防承载能力各项指标的测定，且可以对不同堤防段的土层进行原位测定，代表性较高，其缺点在于需要较多的人力和物力试验观测，因此不适合于大型河道的堤防承载力的试验测定。

2)随着静力荷载的增加河道堤防土层压缩系数先减后增，这主要是当静力荷载增加时，由于先增加了其孔隙比，使得其沉降的压缩系数有所减少，当孔隙比增加到一定程度后，压缩系数逐步加大，并趋于稳定变化。

3)在进行较大河流堤防承载力原位观测试验时，建议土层残余强度指标的原位测定，从而综合判定其堤防的承载能力。