基于改进粒子群算法的PMSM多参数辨识

柯贤伟，张金亮，彭国生，高云，王志虎，简炜

（1.湖北汽车工业学院 电气与信息工程学院，湖北 十堰442002；2.东风汽车动力零部件有限公司，湖北 十堰442000）

永磁同步电机（permanent magnet synchronous motor,PMSM）因其体积小、重量轻、效率高，在工业领域广泛应用。实际控制系统中PMSM 参数通常难以直接测量，且随着环境温度的变化而变化［1］；而在矢量控制的双闭环控制系统中，电流内环控制器参数的整定需要交直轴电感和定子电阻的值，转速外环控制器的参数设计需要依赖永磁体磁链和转动惯量的值［2］。因此实现电机参数的准确辨识，对电机控制系统的稳定性发挥着重要作用［3］。文献［4］通过分析电机的等效电路，使用静态有限元模型得到铁损电阻和交直轴电感的公式，但模型求解较复杂且推导过程中没有考虑电机实际加工产生的误差。文献［5］运用协同粒子群算法，先辨识出电机定子电阻、定子电感、永磁体磁链，再将辨识出的磁链代入电机运动方程计算转动惯量与负载转矩。由于磁链辨识误差的存在，会额外增加转动惯量与负载转矩的辨识误差。文献［6］提出了惯性权重自适应更新公式来改进粒子群算法，但只辨识出2 个参数，且误差较大。为提高PMSM参数辨识性能，文中在标准粒子群算法（standard particle swarm optimization, SPSO）的基础上使用自适应自治群组粒子群优化算法（adaptive autonomous groups particle swarm optimization,AAGPSO）。首先针对SPSO 采用线性递减策略更新惯性权重的不足，改用自适应更新策略；然后针对SPSO中不变的个体认知系数和社会认知系数，将整个粒子群体分为4个小群组，而后赋予每个粒子小群组认知系数非线性更新策略，增加算法的全局搜索能力；最后基于PMSM 电压方程建立参数辨识模型，使用AAGPSO 对电机参数电子电阻、交轴电感、直轴电感、永磁体磁链进行参数辨识仿真实验。

1 永磁同步电机数学模型

PMSM 是强耦合非线性控制对象。为了便于研究，忽略电机铁芯的饱和效应、永磁体电导率；视电机反电动势为标准正弦信号；不计铁损，则在dq轴坐标系下PMSM定子电压方程可写为

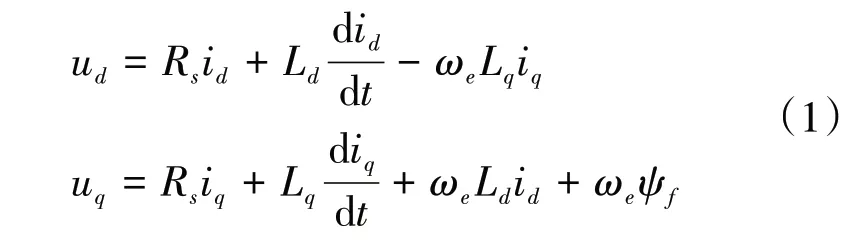
式中：ud和uq为定子电压的交直轴分量；id和iq为定子电流的交直轴分量；Rs为定子电阻；Ld和Lq为交直轴电感；ωe为电角速度；ψf为永磁体磁链。当PMSM稳定运行时，id和iq的波动变化很小，其微分算子可近似为0，因此定子电压方程可简化为

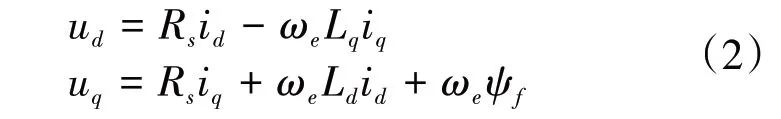
式（2）中有4 个待辨识参数Rs、Ld、Lq、ψf，但方程只有2个，即秩为2，是欠秩方程组。正常情况下无法进行辨识。基于此，在id= 0 的矢量控制策略下，待电机稳定运行后采集相应的电压、电流、转速，再在电机的交轴短时注入1 个id≠0 的负序弱磁电流，采集相同的数据，采样策略如图1 所示。根据采样的数据便可建立离散的满秩方程组：

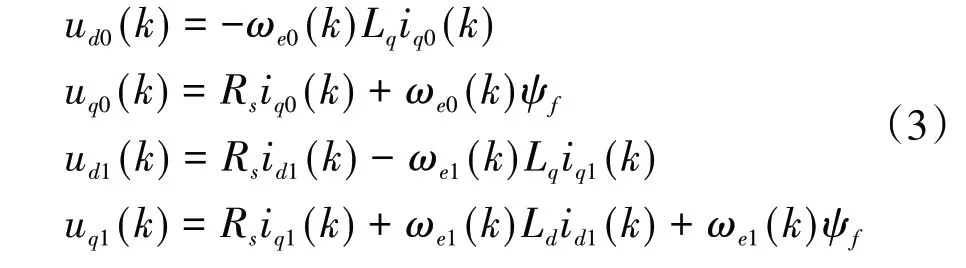
式中：ud0(k)、ωe0(k)、iq0(k)、uq0(k)为图1 中t0～t1时间内第k 次采样的数据；ud1(k)、id1(k)、ωe1(k)、iq1(k)、uq1(k)为图1 中t1～t2时间内第k次采样的数据。

图1 采样策略图

2 标准粒子群算法

粒子群算法是基于群体协作的随机搜索算法，通过模拟鸟群飞行觅食演化而成。通过在一定范围内随机产生N个D维粒子来完成初始化，每个粒子即1 组候选解；然后通过目标函数计算粒子的适应度值，用来评判粒子当前所处位置的好坏，即衡量解的好坏。

依次计算粒子的适应度值，将第i 个粒子历史经过的最好位置记为其个体最优值Pbi，将整个粒子群群体历史经过的最好位置记为全局最优值Gb；再根据式（4）更新每1个粒子的速度与位置。

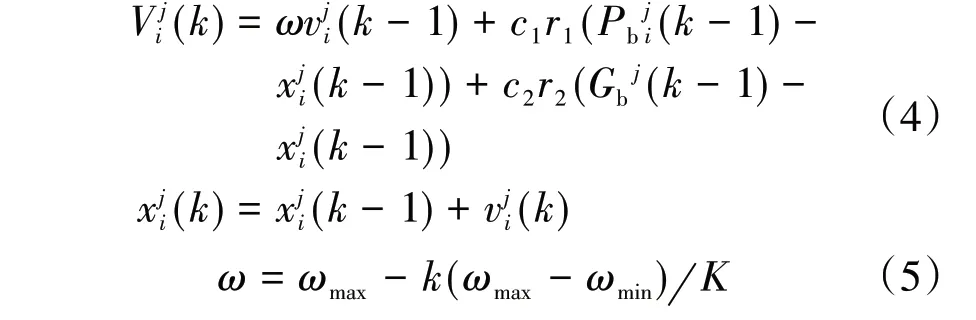
为了便于理解，设随机产生粒子的维度为1维，根据式（4）得到粒子飞行速度和位置更新图（图2）。设粒子i 在第k 次迭代更新后，以速度vi(k)移动到了位置Xi(k)，而粒子i 当前历史最优位置Pbi(k)和整个群体历史最优位置Gb(k)的分布如图2 所示，那么vi(k + 1)就是粒子i 进行第（k + 1）次迭代时根据第k 次迭代速度、历史搜索最好位置、整个群体历史搜寻最好位置共同确定的移动速度。

图2 粒子飞行速度与位置更新图

3 改进粒子群优化算法

3.1 自适应自治群组粒子群算法

为了更好地协调粒子群算法在整个迭代过程中惯性部分和认知部分之间的占比，针对式（5）中SPSO 对惯性权重ω 线性化更新的不足，使用非线性自适应惯性权重更新策略：

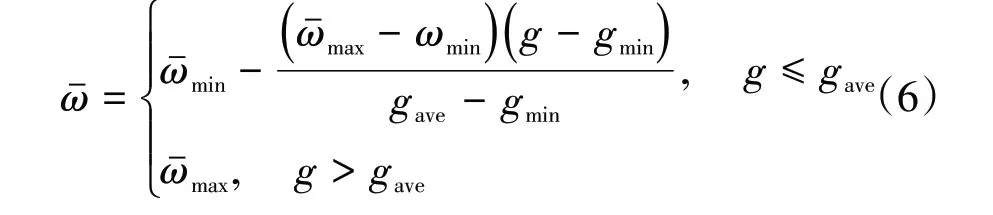
表1 粒子小群体的认知系数定义表

3.2 自适应自治群组粒子群算法性能测试

为测试AAGPSO的性能，引入3种标准函数进行检验，将AAGPSO 同SPSO 对比实验。测试函数见表2，F1和F2是单峰函数，用来评判被测算法的局部搜寻的能力；F3是多峰函数，用来评判被测算法逃出局部最优、搜寻全局最优的能力。实验设置如下：群体粒子总数50，算法最大迭代次数为500，F1、F2和F3分别以20维、20维、2维的形式作为目标函数被优化，将3个测试函数各自的实际最小值看作全局最优解，使用AAGPSO和SPSO进行优化。

AAGPSO 和SPSO 对测试函数F1、F2、F3的优化曲线如图3 所示。图3a 中虽然AAGPSO 在第15～150次迭代之间搜寻的最优解没有SPSO搜寻的最优解更逼近实际最优解0，但是大约在150 次迭代后AAGPSO 优化结果明显好于SPSO，并且随着迭代次数的增加，AAGPSO的精度优势越来越大。在图3b 和图3c 显示的整个迭代过程中，AAGPSO 的精度均高于SPSO，并且图3c 优势更明显，这也体现了其对多峰值优化问题跳出局部最优的能力。

表2 测试函数

图3 测试函数的优化曲线图

综上所述，AAGPSO 和SPSO 均可通过一次次迭代慢慢逼近全局最优解，但就逼近全局最优值的程度来说，AAGPSO 更加明显，因此可以认为AAGPSO的寻优能力在一定程度上要好于SPSO。

4 AAGPSO的PMSM参数辨识

基于AAGPSO 的PMSM 多参数辨识，核心思想是将电机双闭环控制系统的采样值同算法理论计算值进行比较，经过一次次迭代使得两者无限逼近，同时利用目标函数计算每次迭代后的适用度值，得出目标函数适用度最小的电机参数即算法搜寻的最优值。目标函数f构建如式（7）所示：

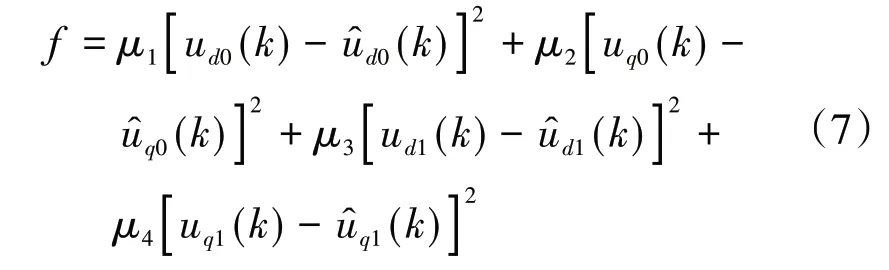
式中：ud0(k)和uq0(k)为图1中t0～t1时间内第k次采样的交直轴电压；ud1(k)和uq1(k)为图1中t1～t2时间内第k 次采样的交直轴电压；ˆd0(k)、ˆd1(k)、ˆq0(k)、q1(k)为根据辨识结果计算出的交直轴电压值；μ1、μ2、μ3、μ4为权重系数，取值均为0.25，因为目标函数中包含的4项对实际电机辨识模型具有同等的影响。AAGPSO辨识PMSM参数的流程见图4。

图4 基于AAGPSO的PMSM参数辨识流程图

5 实验仿真

5.1 实验设计

图5 PMSM参数辨识仿真模型框图

为了验证AAGPSO同时辨识PMSM定子电阻、交轴电感、直轴电感、永磁体磁链的可行性和有效性，在Matlab/Simulink 中搭建仿真实验模型，具体框图见图5。仿真参数设置如下：Rs为0.958 Ω，Ld和Lq为5.25 mH，转动惯量J 为0.003kg·m2，ψf为0.1827 Wb，阻尼系数B 为0.008 N·m·s，极对数Pn为4。在PMSM稳态时，分别在id= 0与id≠0的矢量控制策略下采样，单次采样时间为1μs，即在图1中t0～t1内以1μs为周期采样10 000组数据，以同样方法在t1～t2内采样10 000组数据，从中选出对应的200组数据代入AAGPSO进行电机参数辨识。

为体现AAGPSO 的性能，仿真实验中增加SP⁃SO、IPSO、TACPSO 对比，IPSO（improved particle swarm optimization）认知系数c1和c2的更新策略与AAGPSO粒子群组Group3相同，TACPSO（timevary⁃ing acceleration coefficients particle swarm optimiza⁃tion）认知系数c1和c2的更新策略与AAGPSO 粒子群组Group4 相同。4 种算法的粒子数均为150，最大迭代次数200次。

5.2 实验分析

4 种算法对PMSM 参数辨识的结果如表3 所示，适应度变化曲线见图6。实验中4 个参数具体的辨识曲线如图7 所示。由图6 可看出：AAGPSO的适应度值最小，说明AAGPSO对4个参数的整体辨识精度最高。由表3和图7可以看出：虽然IPSO对ψf的辨识精度大于AAGPSO，但对其他3个参数的辨识精度均小于AAGPSO；虽然TACPSO对Rs的辨识精度高于AAGPSO，但对其他3个参数的辨识精度均小于AAGPSO；而SPSO 对4 个参数的辨识精度均小于AAGPSO。因此AAGPSO 对4 个参数的辨识整体效果较好，与图6显示的结果相契合。

表3 参数辨识结果

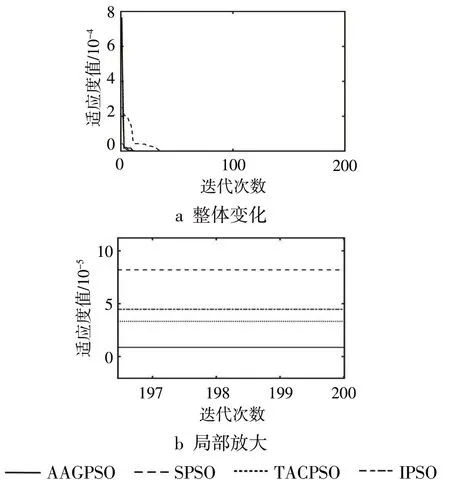
图6 适应度变化曲线

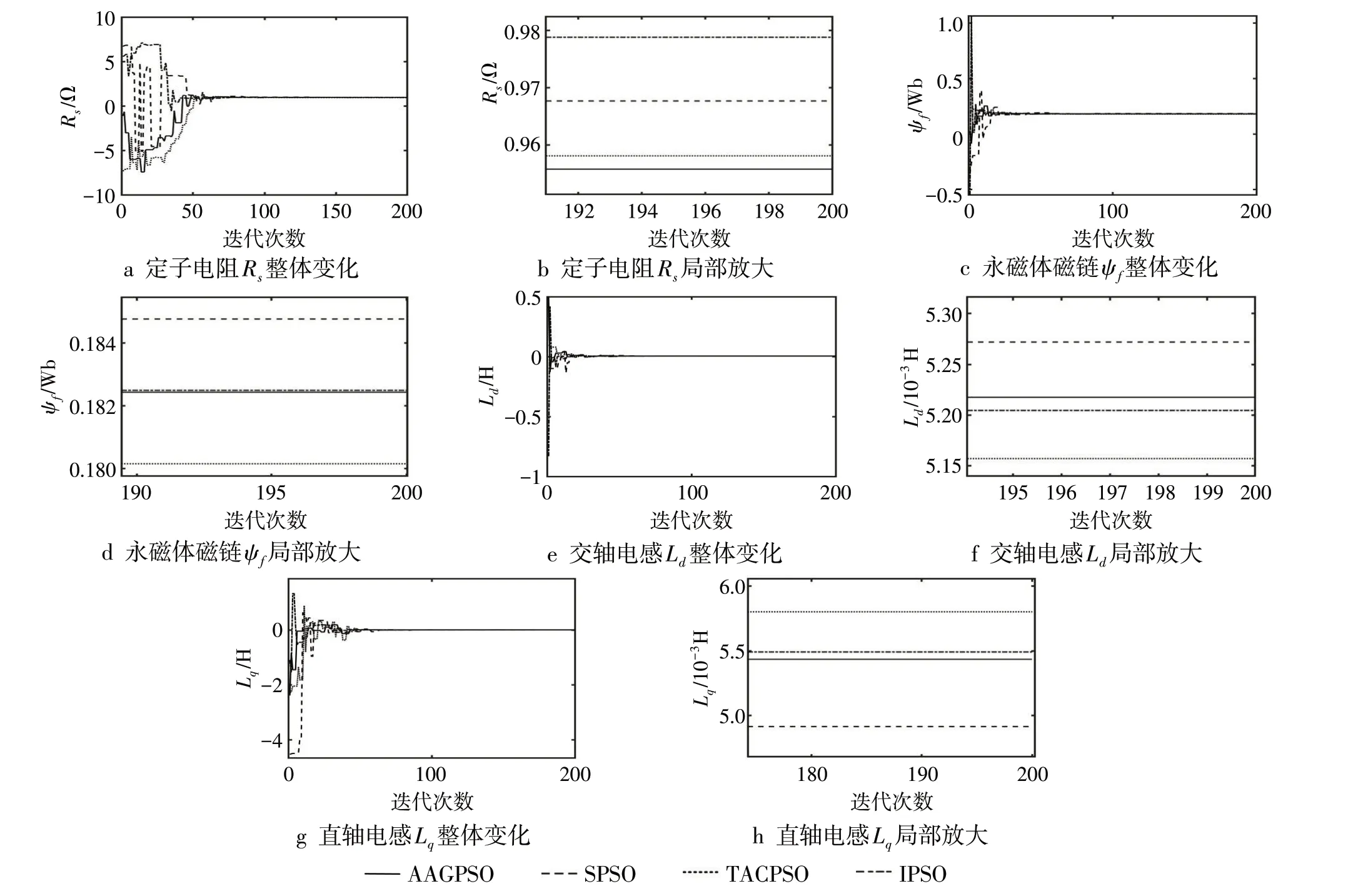
图7 参数辨识曲线

6 结论

针对PMSM 参数辨识难的问题，在SPSO 的基础上，将AAGPSO应用到PMSM参数辨识中能同时辨识4 个参数。仿真实验结果表明AAGPSO 辨识结果在整体精度上高于其他粒子群优化算法。