基于模型预测控制的智能车横纵向控制器设计

吴昊，王思山，周海鹰，商蓉侦

（1.湖北汽车工业学院 汽车工程师学院，湖北 十堰442002；2.东风商用车有限公司 车辆工厂，湖北 十堰442000）

车辆在运动过程中具有非线性、强耦合效应等特性，如何有效提高车辆的跟踪精度，改善车辆的行驶稳定性是当前的主要研究目标。车辆路径跟踪控制研究主要分为纵向控制、横向控制以及横纵向综合控制。纵向控制方面，Volkan sezer［1］通过获取车辆与目标障碍物之间的危险距离与最近障碍物的夹角计算周围的障碍物系数，利用模糊算法规划车辆的安全车速并对车辆施加控制。横向控制方面，Chongfeng Wei［2］通过研究人类驾驶员的驾驶行为习惯及车辆的动态性能，提出基于安全走廊的非线性模型预测控制，利用安全走廊的行驶施加轨迹约束，实现平稳舒适的轨迹跟踪控制。横纵向控制方面，Alia Chebly［3］利用所建立的车辆模型推导出车辆横纵耦合规律，提出2种耦合控制器，第1种控制器采用Lyapunov控制方法，第2种控制器采用滑模变结构控制，能够保证对参考轨迹和期望速度的鲁棒跟踪，同时考虑车辆横向和纵向动力学之间的强耦合。Fen Lin 和Yaowen Zhang［4］等人研究了纵向-横向控制方法与偏航稳定性在自动驾驶汽车轨迹跟踪中的结合。谢晖［5］等人根据车辆运动学模型建立基于模型预测控制算法的横纵向控制系统，基于典型参考速度模型实现横纵向控制。但都没有考虑到在基于车辆动力学的横纵向控制中加入参考速度的实时规划。文中提出基于道路曲率信息和横向误差反馈的横纵向综合控制方法，对车辆轨迹跟踪问题进行研究。

1 MPC横纵向控制策略

车辆横纵向控制策略见图1，根据参考路径提供的曲率Kref、横向位置Xref、纵向位置Yref以及车辆反馈的状态量信息，通过横纵向控制实现车辆的路径跟踪。首先对道路信息进行提取，速度规划模块根据输入的Kref以及车辆反馈的横向位移误差e，通过模糊算法计算后输出参考速度Vref，MPC 纵向上层控制器对参考速度进行跟踪控制并输出期望速度vdes与期望加速度ades。将vdes输入至MPC 横向控制器，ades输入至纵向下层控制器，通过逆纵向动力学模型，输出发动机节气门开度信号ua与制动主缸压力信号ub。根据MPC 横向控制器提供的Xref、Yref和MPC纵向上层控制器提供的vdes以及车辆模型反馈的状态量信息，通过车辆动力学模型求解车辆前轮转角δf。将输出控制量ua、ub以及δf输入至车辆模型。循环上述求解，最终完成车辆运动控制。

2 纵向速度规划

2.1 基于模糊逻辑的速度规划方法

采用模糊逻辑方法，根据当前路径的曲率以及车辆与参考轨迹的横向位移误差对车辆纵向速度进行规划。

函数的输入为道路曲率、横向跟踪误差，模糊语言值设置为B（大）、M（中）、S（小）。隶属函数选择钟形函数：

式中：abell、bbell、cbell为广义钟形隶属函数参数，abell决定了当隶属函数隶属度为0.5时的横轴位置，bbell决定了隶属度变化速度的快慢以及函数的开口方向，cbell决定了隶属函数的中心所在位置。

函数的输出为车辆纵向速度，模糊语言设置为VB（非常大）、B（大）、LB（较大）、M（中）、LS（较小）、S（小）、VS（非常小）。隶属函数选择三角形函数：

式中：atri、btri、ctri为三角形隶属函数的参数，决定了隶属度曲线三处顶点的横坐标位置。模糊逻辑规则如表1所示，模糊推理曲面如图2所示。

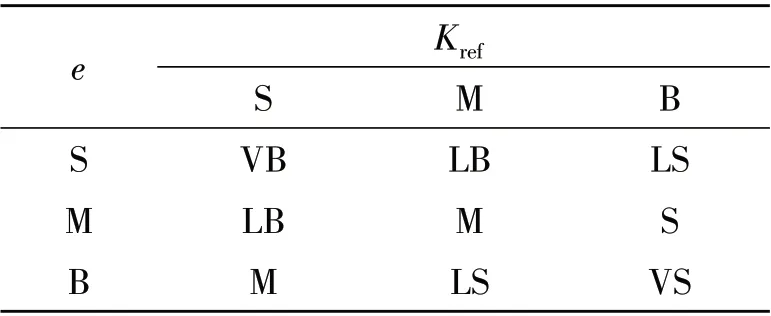
表1 模糊逻辑规则

图2 模糊推理曲面

2.2 路径曲率的滑动平均滤波处理

根据几何三角关系计算路径曲率：式中：Li-1,i、Li,i+1、Li-1,i+1为目标路径上连续的3个轨迹跟踪点相互之间的距离；K（i）为路径原始曲率。通过滑动平均滤波算法对路径曲率进行滤波处理以减小振荡，输出合理的车辆目标速度。滑动平均滤波算法为

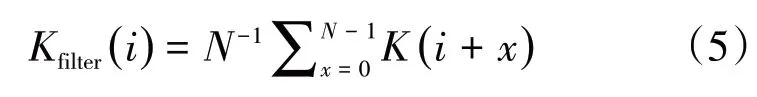
式中：K为利用连续目标路径点之间的距离计算出的原始路径曲率；Kfilter为经过滑动平均滤波处理后的曲率；N为滑动窗口的大小。路径曲率在经过滑动平均滤波处理后，按照不同的大小范围进行分区域拟合，使得输出的目标车速连续平稳，且避免了制动/驱动模式的频繁切换。

2.3 纵向目标车速的去模糊化

获得模糊算法输入量后，通过所选择的隶属函数，计算路径轨迹曲率、横向跟踪误差2 个输入分量各自在不同模糊子集的隶属度。去模糊化方法采用加权平均法：

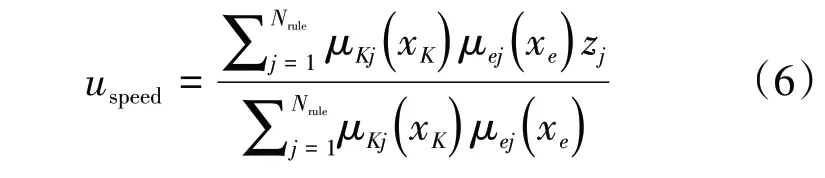
式中：Nrule为激活的模糊规则数目；μKj（xK）、μej（xe）分别代表曲率、横向误差在被激活的第j 条模糊规则中各自所在模糊子集中的隶属度；zj为不同模糊规则内，输出uspeed所在模糊子集隶属度函数的顶点所在位置的横坐标值。将得到的目标速度曲线进行二次规划，对加速度和加速度变化率进行约束。根据文献［6］，加速度a（k）上限为3.07 m·s⁻²，减速度上限为5.08 m·s⁻²，加速度变化率Δa限制在±2 m·s⁻³以内。纵向目标车速与纵向目标加速度输出为

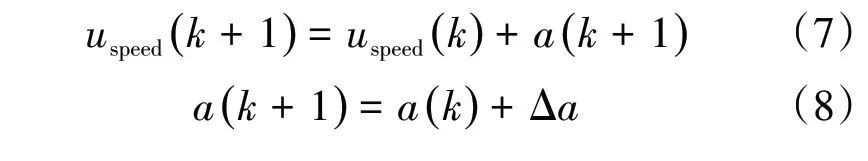
3 基于MPC的纵向控制器设计

3.1 MPC上层控制器设计

车辆行驶时，忽略横摆运动对车辆纵向运动特性影响，近似认为车辆纵向加速度等于纵向速度的一阶导数［7］：

式中：ax为纵向加速度；vx为纵向速度。利用一阶延时环节可以得到：

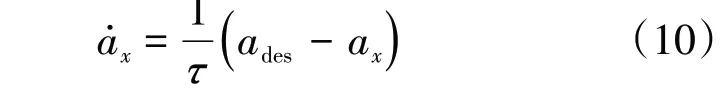
式中：ades为期望加速度；τ 为时间常数，取值0.2。连续系统的状态量为ξL=［vxax］T，输入量纵向速度为uL=［ades］。连续系统状态方程为

将式（11）离散化得到离散系统状态方程为

式中：t 为当前采样时刻；（t+1）为下一采样时刻；T为采样周期。系统输出量为车辆速度yL（t）：

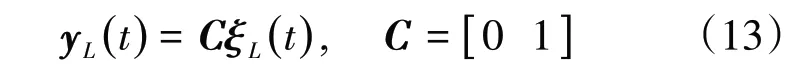
为了使车辆以平稳的加速度以及加速度变化率实现对参考速度的精确跟踪，设计目标函数为

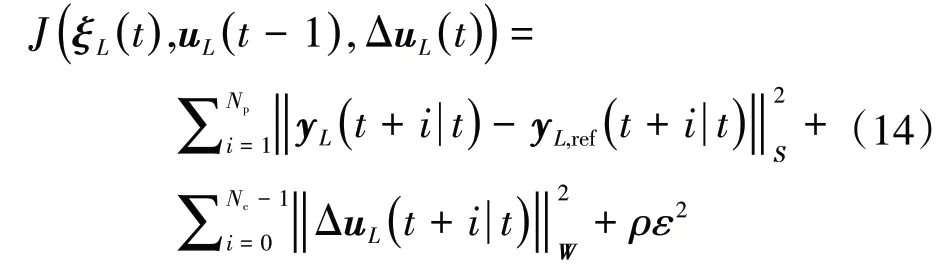
式中：Np为预测时域；Nc为控制时域；y（t+i|t）为系统输出的预测值；yref（t+i|t）为系统输出的参考值；（t+i|t）表示根据系统t 时刻的状态信息预测t+i 时刻的状态信息；S、W 为权重矩阵；ρ 为权重系数；ε为松弛因子。约束条件设计主要考虑控制量约束以及控制增量约束：

式中：uL（t+i）为当前时刻的加速度控制量；ΔuL（t+i）为当前时刻的加速度控制增量；uLmin和uLmax为纵向加速度约束最小值和最大值；ΔuLmin和ΔuLmax为纵向加速度变化约束的最小值和最大值。

3.2 下层控制器设计

车辆正常行驶时，为了避免对汽车系统造成损伤，不能同时操作油门和制动踏板，同时为了保证乘坐舒适性，不能频繁切换制动与驱动模式［8］。根据汽车行驶时的期望加速度来设计模式切换逻辑：

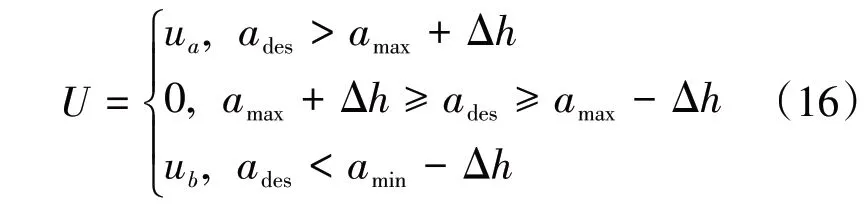
式中：U 为输出模式；amax为节气门开度为0 时的汽车最大制动减速度；Δh为模式切换区间缓冲值，作用是避免驱动/制动模式切换频繁。

1）驱动模式 假设车辆在平直且路面状况良好的道路上行驶，忽略道路坡度阻力以及车辆内部的旋转构件换算质量，可以得到：

式中：m为车辆质量；Fd为系统所需驱动力；Fa为车辆当前受到的空气阻力；Ff为车辆当前受到的滚动阻力；ρa为空气密度；Af为车辆迎风面积；Cd为空气阻力因数；Cr为滚动阻力因数。利用上述汽车纵向动力学模型得出发动机所需的输出扭矩为

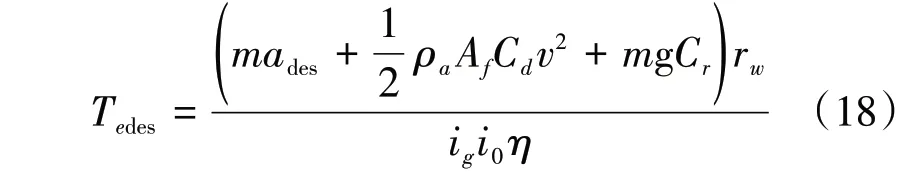
式中：rw为轮胎半径；ig为变速器传动比；i0为主减速器传动比；η 为机械传动效率。通过得到的Tedes及所知的发动机转速n，结合节气门开度三者之间的关系得出节气门开度所需控制量：

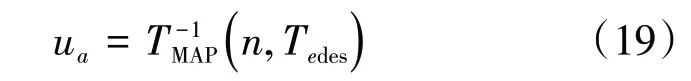
2）制动模式 制动模式下，车辆节气门关闭，发动机无扭矩输出，系统输出制动主缸压力。忽略坡道阻力，得到

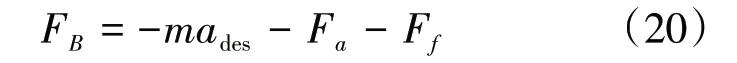
车辆处于制动模式时，假设轮胎不发生抱死，则制动系统油路压力与制动器的制动压力的关系为

式中：KB为换算系数；Pdes为所需制动压力。则所需制动压力为

4 基于MPC的横向控制器设计

4.1 车辆模型

在建立车辆动力学模型时进行相应简化［9］：1）采用自行车模型，忽略载荷的左右转移以及前后轴的载荷转移；2）假设无人驾驶车辆行驶路面平坦，忽略车辆垂向运动；3）假设车辆与悬架系统为刚性，忽略悬架系统作用；4）假设轮胎侧偏特性为线性关系。车辆动力学模型为

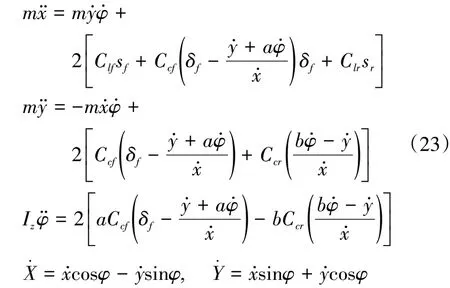
式中：m 为整车质量；φ 为车辆横摆角；φ̇为车辆横摆角速度；φ̈为车辆横摆角加速度；a为车辆前轴到质心的距离；b为车辆后轴到质心的距离；Iz为车辆绕z轴的转动惯量；δf为车辆前轮转角；Ccf和Ccr为前后轮胎侧偏刚度；Clf和Clr为前后轮纵向刚度；sf和sr为车辆前后车轮滑移率；x 为车辆在x 轴方向的速度；ẍ为车辆在x 轴方向的加速度；ẏ为车辆在y 轴方向的速度；ÿ为车辆在y轴方向的加速度；Ẋ为车辆在地面坐标系X轴方向的速度；Ẏ为车辆在地面坐标系Y轴方向的速度。

4.2 横向控制器设计

根据车辆动力学模型，式（23）表示为

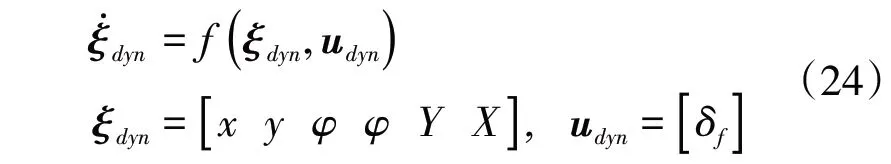
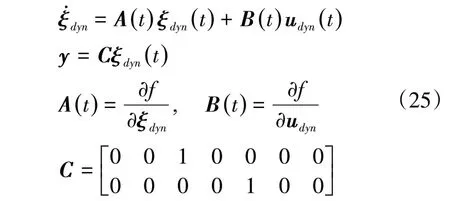
式中：y为系统输出。通过离散化将该问题转换为最优控制问题：

式中：T为采样周期；I为单位矩阵。为了保证车辆在行驶过程中能够准确平稳地跟踪参考路径，设计合理的目标函数可计算得到一系列最优控制量，目标函数为

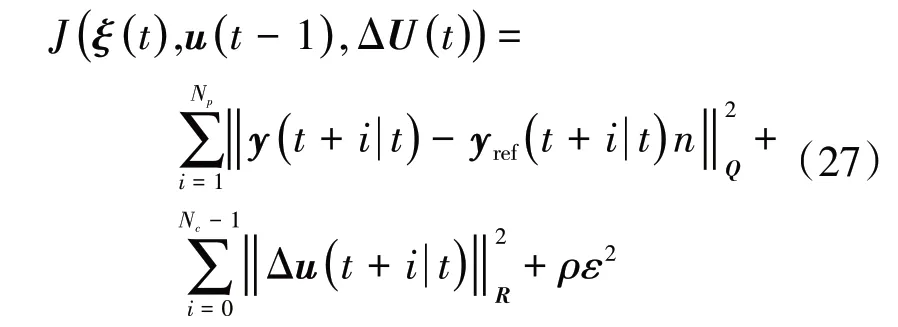
式中：Np为预测时域；Nc为控制时域；Q和R为权重矩阵；ρ为权重系数；ε为松弛因子。由于在车辆路径跟踪过程中，对于车辆稳定性，动力性等方面的考虑，需要对车辆添加控制量约束以及控制增量约束。则系统在每个周期内求解以下优化问题：

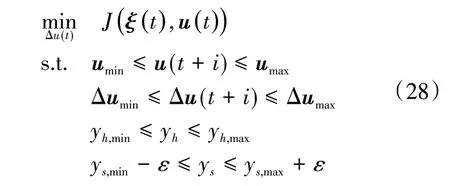
式中：u（t+i）为当前时刻的车辆前轮转角控制量；Δu（t+i）为当前时刻的车辆前轮转角控制增量；umin和umax为车辆前轮转角约束的最小值和最大值；Δumin和Δumin为车辆前轮转角变化量约束的最小值和最大值；yh,min和yh,max为硬约束输出量的上限和下限；ys,min和ys,max为软约束输出量的上限和下限。系统在每个周期内完成最优求解，得到每个周期控制时域Hc内的一系列控制输入增量：

将该控制增量序列中的第1 个控制增量作为系统的实际控制输入增量作用于系统，即

5 仿真验证

为验证横纵向控制策略的可行性与准确性，根据表2 数据在Carsim 中建立车辆模型及相应测试场景，通过Matlab/Simulink 设计控制算法。采用B-Hatchback车型，实验工况为双移线工况［10］。

MPC控制器预测步长为20，控制步长为2，采样时间T为0.05 s，权重系数ρ为1000。权重取值为不同路面附着系数对车辆在弯道行驶时的转向角控制量以及速度控制量输出有较大影响，实验中路面附着系数μ 设置为0.85。仿真实验选择有无纵向速度规划进行对比，仿真时间为15 s。策略A即恒速MPC 横向控制，车辆横向控制采用MPC 控制器，纵向控制速度为52 km·h⁻¹；策略B即MPC横纵向控制，车辆横向控制采用MPC控制器，纵向控制采用带有速度规划的MPC纵向控制器。

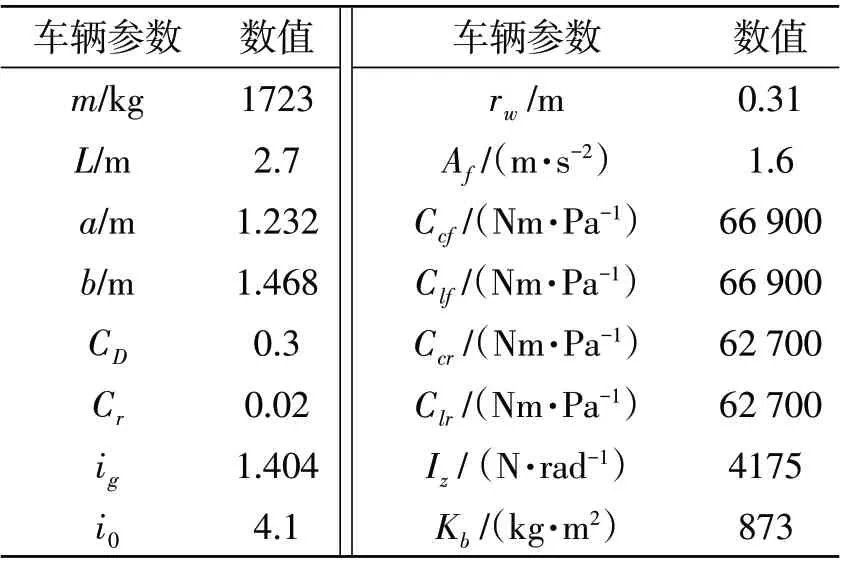
表2 车辆模型参数

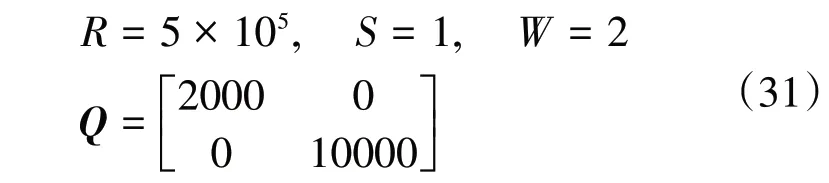
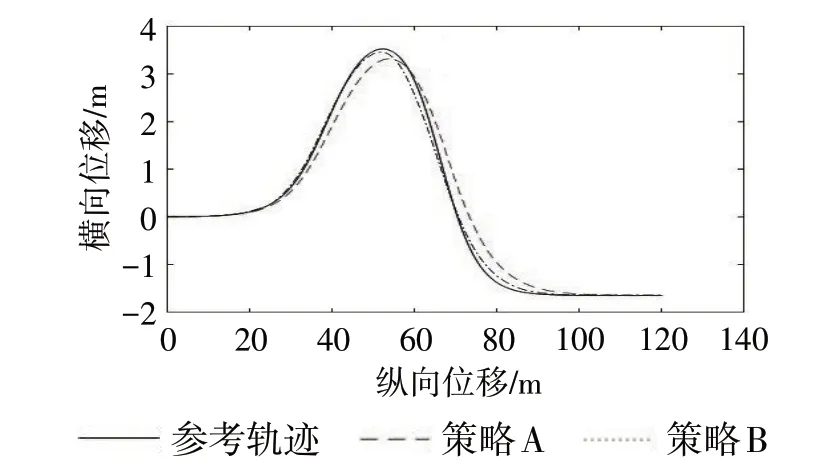
图3 横向位移输出量随纵向位移变化关系

图4 横向位移误差随纵向位移变化关系

无人驾驶车辆在行驶时，车辆速度不同对路径跟踪的误差有较大影响。如图3～4所示，车辆在采用策略A 行驶过程中车速为52 km·h⁻¹，高于采用策略B时的车速，车速对于车辆的动力学参数影响较大，车速越高，控制器的轨迹跟踪性能越差，车辆的路径跟踪横向误差较大，故策略B中基于模糊逻辑的速度规划模块输出较低的车速以降低横向误差，采用策略B时横向位移误差绝对值小于0.3 m。由图5可以看出，采用策略B时车辆在曲率较大处前轮转向角大于采用策略A时的前轮转向角，因为在曲率较大处采用策略A 时的车速大于采用策略B 时的车速，于同样曲率的弯道，车辆采用策略B所需的前轮转角较大，且在曲率较大位置前轮转角出现抖动，此时车速较低，车辆几乎完全跟踪目标路径，变化较为灵敏。采用策略B的横向位移误差明显小于采用策略A时的横向位移误差。

车辆纵向速度控制结果如图6～7 所示。在2次制动/驱动模式切换时出现了一定程度的控制量偏差。在模式切换及速度突变时，曲线跟踪会出现一定程度误差，但是误差绝对值小于0.4 m·s⁻¹，最大速度误差为0.393 2 m·s⁻¹，速度均方根误差为0.099 41 m·s⁻¹，能够实现合理的速度跟踪。

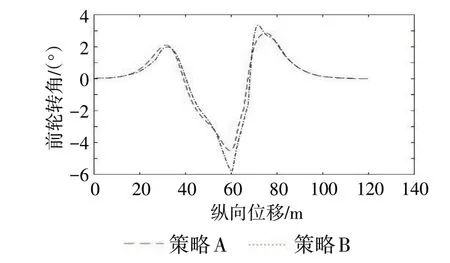
图5 车辆前轮转角随纵向位移变化关系

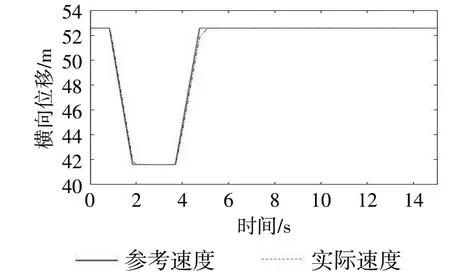
图6 行驶速度随时间变化关系

图7 速度跟踪误差随时间变化关系

车辆控制量节气门开度信号与制动系统压力信号如图8～9 所示，可以看出制动/驱动逻辑切换模块满足车辆系统制动与驱动不能同时操作的要求，且控制过程中没有频繁切换制动/驱动模式，保证车辆平稳行驶，提高了乘坐舒适性。

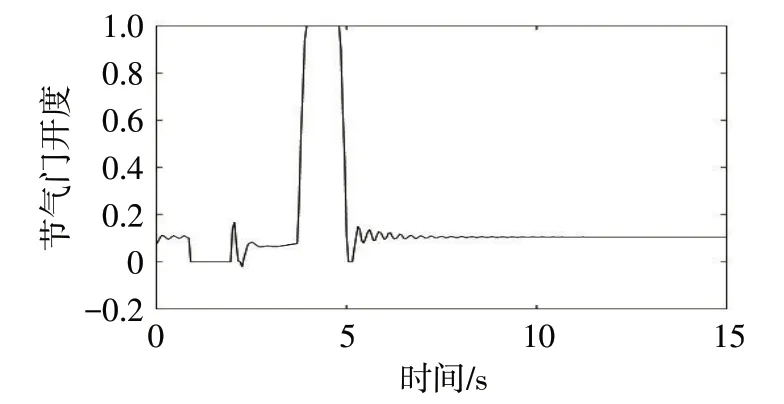
图8 节气门开度输出量随时间变化关系

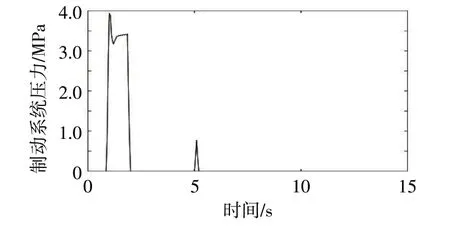
图9 制动系统压力输出量随时间变化关系

为了更好地对比策略A与策略B的控制效果，控制器控制误差如表3所示，可以看出策略B在跟踪误差的控制误差均小于策略A，故所提出的策略B在控制精度方面明显优于策略A。

表3 不同策略的跟踪误差 m

6 结论

文中提出基于MPC的智能车横纵向跟踪控制方法。通过仿真实验对比MPC横纵向控制与恒速MPC 横向控制的效果，结果表明：1）相比于恒速MPC横向控制，横纵向控制降低了横向位移误差；2）采用横纵向控制策略时，纵向最大速度跟踪误差为0.393 2 m·s⁻¹，速度均方根误差为0.099 41 m·s⁻¹，满足速度跟踪要求；3）采用横纵向控制策略时，制动/驱动模式切换满足两者不可同时作用且不可频繁切换的要求，提高了车辆的稳定性及乘坐舒适性。因此采用横纵向控制策略能够有效地满足无人驾驶车辆对纵向速度和横向位移的跟踪要求。