可获得发射分集的正交空频索引调制算法

聂高阳，王磊，李灿霖

(西安交通大学电子与信息学部，710049，西安)

多输入多输出(MIMO)技术是提高无线通信网络的系统容量和可靠性的关键技术之一,由于它在发送端和接收端都使用多根天线,在收发之间构成多个信道的天线系统,因而极大地提升了信道容量。MIMO系统具有极高的频谱效率,在对现有频谱资源充分利用的基础上通过利用空间资源来获取可靠性与有效性两方面增益,但是其代价却是增加了发送端与接收端的处理复杂度。MIMO系统在一定程度上可以利用传播过程中的多径分量来抵抗多径衰落,但是对于频率选择性衰落,MIMO系统依然是无能为力的。解决MIMO系统中的频率选择性衰落的有效途径是利用正交频分复用(OFDM)技术。

对于MIMO-OFDM的研究已经有很多[1-5],但是OFDM的子载波正交性在高速移动环境下会遭到破坏从而导致载波间干扰(ICI),针对此问题,文献[6]提出了正交频分复用索引调制(OFDM-IM)技术,其中每个OFDM块只有部分子载波被激活用来传输信息从而减轻ICI,但是由于未被激活的空闲子载波数量受输入信息比特的影响,因此与OFDM相比,OFDM-IM以降低频谱效率为代价来增强误比特率性能,理论分析也表明OFDM-IM可以在误比特率性能和频谱效率上实现一定的折中[7-10]。为了获得频率分集,文献[11]通过集成子载波级的块交织器来改善OFDM-IM的传统结构,提出了带交错子载波的OFDM-IM(OFDM-ISIM),这种结构能够增加接收符号之间的欧氏距离从而实现性能改进。OFDM-IM虽作为最初的原理提出具有意义,但实用性差,多模正交频分复用索引调制(MM-OFDM-IM)能够克服这一缺点[12-13],在该类算法中,子载波被分成多组,对应于多个索引子集。多组子载波通过多种不同的星座模式进行调制,并且可以通过多个索引子集之一来确定通过索引调制传送的信息比特,这样就对所有子载波进行了调制,从而提高了OFDM-IM的频谱效率。

基于IM和MIMO-OFDM的优点,文献[14-15]通过将MIMO-OFDM和上述OFDM-IM相结合而提出的MIMO-OFDM-IM是一种高性能多天线多载波传输技术。在该算法中,每个发送天线都发送独立的OFDM-IM块以提高数据速率,与传统MIMO-OFDM相比,MIMO-OFDM-IM具有更好的误比特率性能和更低的天线/子载波间干扰。

但是,MIMO-OFDM-IM仅仅在频域进行了索引调制,而文献[16-17]将IM的思想推广到频域联合空间域中,提出了广义空频IM(GSFIM)算法,该算法在空域的天线和频域的子载波的索引中都对信息比特进行了编码,通过利用空间域中的索引,可以将GSFIM视为MIMO-OFDM-IM的扩展。随后,鉴于信号星座具有同相和正交分量,文献[18]对MIMO-OFDM的资源块(RB)中的空频单元的索引号进行两次独立地激活,分别用于发送信号的同相和正交分量,从而提出了正交SFIM(QSFIM)算法,文献中证明了该算法可以在不增加能量消耗成本的情况下提高数据速率,从而进一步提高MIMO-OFDM的能量效率。但是,上述文献仅在空间域和频率域使用了索引调制技术,其实在时间域和信道域也可以采用索引调制技术,文献[19]对这些内容进行了总结概括。

然而,上述算法并不能获得发射分集,从而不能有效抵抗信道衰落带来的不利影响,因此文献[20-21]针对一些空间域上的IM算法不能获得发射分集的情况提出了一些解决方案。

在这种背景下,本文提出了一种适用于MIMO-OFDM系统中的可获得发射分集(TDA)的正交空频索引调制算法,简称TDA-QSFIM算法。该算法一次发送两个调制符号,然后通过哈达玛矩阵和旋转矩阵将这两个符号关联起来构造对角码,并扩展为同相和正交分量,再由RB中不同的空频单元调制后进行发送,从而在每个RB上进行了有效的码字设计,获得了二阶发射分集,因此TDA-QSFIM算法的性能好于现有的QSFIM算法。仿真实验进一步验证了理论分析的正确性和本文所提TDA-QSFIM算法的性能优势。

1 系统模型与TDA-QSFIM算法

考虑一个具有Nt个发射天线和Nr个接收天线的MIMO-OFDM系统,每对收发天线间的信道为频率选择性瑞利衰落信道。假设OFDM子载波的数量为N。将N个子载波的总数划分为ng个子块,每个子块具有n个子载波,即ng=N/n。具有Nt个发射天线的每个子块上的n个子载波形成一个RB,其中包含nNt个空频资源单元。以下将通过在每个RB上设计编码的方法使得正交IM传输获得发射分集。

1.1 本文所提TDA-QSFIM算法

图1 TDA-QSFIM发射机框图

以下以第b个RB上的编码为例来说明编码矩阵的具体构造方法。

当Nt=2时,每个RB的维数是n×2维。考虑第b个RB上的信息比特块,为了获取发射分集,首先使用下列式子对两个调制符号xb,1和xb,2进行关联

(1)

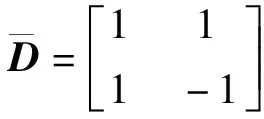
(2)

并且令Db,I与Db,Q分别为Db的同相和正交分量,即

(3)

(4)

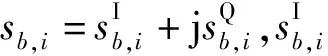
Vb=Vb,I+jVb,Q=eb,k⊗Db,I+j(eb,l⊗Db,Q)

(5)

式中:k,l∈{1,…,n/2};b∈{1,…,ng};⊗表示Kronecker积。

以n=4为例,则TDA-QSFIM的星座集合中会有如下4种矩阵结构

(6)

(7)

(8)

(9)

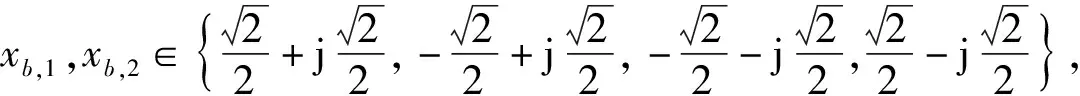
(10)

(11)

则最后所映射的编码矩阵为

(12)

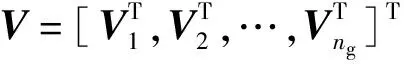
(13)

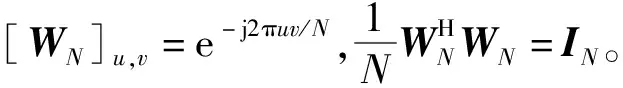
1.2 系统模型

将信号U从两个发射天线上发送出去,经过一些矩阵运算后,系统的等效频域表示式[18]为

(14)

(15)

式中:xb(c)∈RNt是第b个RB中第c个子载波上的传输向量。假定wb的每个元素都是均值为零且方差为N0的独立同分布(i.i.d.)的复高斯随机变量。频域表示式(7)还可以再次表示为

(16)

1.3 最大似然检测

(17)

2 性能分析

本节对所提出的TDA-QSFIM算法的频谱效率、发射分集和旋转角优化问题进行讨论,并推导其误比特率性能的理论公式,最后比较不同算法的ML检测复杂度。

2.1 频谱效率

由1.1节可知,一个RB上能传输的比特数为m=2lbM+2lb(n/2),N个子载波被分为ng组,每组为n个子载波,CP长度为NCP,因此总的频谱效率R为

(18)

式中,R的单位为bit/(s·Hz-1)。

2.2 发射分集

由于每个RB的分集和编码增益性能相同,因此不失一般性并且为了符号表达简洁,在本节中将省略式(5)、式(8)和式(9)中的下标。首先假设TDA-QSFIM编码矩阵为

(19)

式中:元素ai,i、di,i(i=1,2)不为0。

将式(5)中定义的n×2维TDA-QSFIM编码矩阵表示为以下形式

(20)

式中,vi(i=1,2)为V的第i列。按照2.2节中的运算,n×2维TDA-QSFIM编码矩阵可以等价表示为

(21)

式中,diag(·)表示将向量中的元素对角化。被错误检测的编码矩阵可以等价表示为

(22)

定义两者之间的误差矩阵

(23)

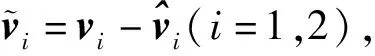
ΔHΔ=

(24)

其中Λi(i=1,2,3)是n×n维对角矩阵,可以将其表示为

(25)

(26)

(27)

其中∘表示向量的对应元素相乘,则

(28)

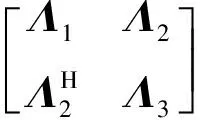
2.2.1 情况1 对角空频码不同,但在RB上的位置相同,则被错误检测的编码矩阵为

(29)

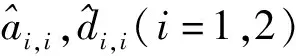
(30)

因此rank(Λ1)=1,同理rank(Λ3)=1,但

Λ2=diag([0,0,…,0])

(31)

2.2.2 情况2 对角空频码相同,但在RB上的位置不同,则被错误检测的编码矩阵为

(32)

根据式(20)～(24)可得下式

Λ1=diag([a1,12+d1,12,0,a1,12+d1,12,0,…,0])

(33)

2.2.3 情况3 对角空频码和在RB上的位置均不同,则被错误检测的编码矩阵为

(34)

由式(20)～(24)原理可得

(35)

因此rank(Λ1)=2,同理可得rank(ΔHΔ)≥4。

由上述分析可知rank(ΔHΔ)≥2,根据空频编码的秩准则,该算法发射分集为2。

2.3 旋转角优化

本节对旋转角θ进行优化,其目的是在确保发射分集阶数为2的同时最大化TDA-QSFIM的编码增益。

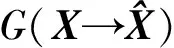
(36)

为了使编码增益最大化,需要对旋转角θ进行优化。需要注意的是由于复数星座图的对称性,θ的取值范围为[0,π/2]。用计算机穷举搜索来计算最大编码增益,从而得出使编码增益最大化的最优旋转角

(37)

针对不同的QAM调制阶数M和每子块子载波个数n,最优旋转角如表1所示。

表1 TDA-QSFIM算法在Nt=2时在不同的QAM调制阶数和每个RB的子载波个数下的最优旋转角

2.4 多径瑞利衰落信道下的误比特率性能

TDA-QSFIM算法在多径瑞利衰落信道下的误比特率(BER)表示式[18]可以写为

(38)

通过将式(16)扩展到所有RB,可以将系统的等效频域表示式写为

(39)

(40)

式中:1为元素全为1的矩阵。协方差矩阵Q可以表示为

(41)

式中:Wn是WN的前n行的子矩阵;Ω是信道多个路径非视距成分功率组成的对角矩阵;Rt是不同发射天线之间的相关系数矩阵;Rr是不同接收天线之间的相关性系数矩阵。可以证明,其他RB的协方差矩阵为nNtNr×nNtNr维子矩阵,这些子矩阵以适当的起始位置沿Q的主对角线居中。

系统的条件成对错误概率(CPEP)可表示为

(42)

(43)

通过对信道系数的随机性进行积分,可以将无条件成对错误概率(UPEP)表示为

(44)

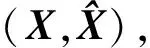
(45)

式中,λi是QA的特征值且v=rank(QA)。因此,PEP的上界可以表示为

(46)

式中使用不等式sin2θ≤1来得到上界。对于高信噪比(SNR),可以将式(46)近似为

(47)

此外,由于Q函数具有近似式

(48)

将式(48)代入式(42),可以将PEP的上界进一步写成

(49)

对于高信噪比,可以将式(49)再次近似为

(50)

2.5 复杂度比较

本小节对MIMO-OFDM-IM算法、QSFIM算法和本文提出的TDA-QSFIM算法做ML检测时的复杂度进行比较。

表2 3种算法的ML检测复杂度对比

3 实验仿真

为了验证本文所提TDA-QSFIM算法的误比特率性能,将其与QSFIM算法的性能进行比较。假设接收端具有理想的信道估计,ng=32,Nt=2,NCP=16,多径数为10。

令Nr=2,每个RB的n=4,R=1.78 bit/(s·Hz-1),采用8QAM调制,旋转角为π/8,图2给出了TDA-QSFIM算法和采用4QAM调制的QSFIM算法、MIMO-OFDM-IM算法在独立同分布瑞利衰落信道上采用ML检测的性能曲线。图3给出了Nr=2,每个RB的n=8,R=2.22 bit/(s·Hz-1)时,采用8QAM调制,旋转角为3π/8的TDA-QSFIM算法和采用4QAM调制的QSFIM算法在独立同分布瑞利衰落信道上采用ML检测的性能曲线。从图2和图3可以看出:TDA-QSFIM算法由于能够获得二阶发射分集,因此比QSFIM算法具有更好的误比特率性能,而且在高信噪比时,也比MIMO-OFDM-IM算法具有更好的误比特率性能;当误比特率为10-5时,TDA-QSFIM算法比QSFIM算法具有大约3.5 dB的性能增益。此外,图2和图3中还给出了TDA-QSFIM算法的BER的理论曲线,可以看出,当信噪比为10 dB时,理论曲线和蒙特卡罗仿真曲线基本相符,因而验证了BER理论分析的正确性。

图2 R=1.78 bit/(s·Hz-1)、Nr=2、n=4时独立同分布瑞利衰落信道上3种算法的BER性能比较

图3 R=2.22 bit/(s·Hz-1)、Nr=2、n=8时独立同分布瑞利衰落信道上TDA-QSFIM与QSFIM算法的BER性能比较

此外,本文还比较了在相关瑞利信道下不同算法的误比特率性能。这里,第u个天线和第v个天线之间的相关系数由[Rx]u,v=J0(2πdx|u-v|)给出,其中发射或者接收天线间距为dx(以波长为单位),其中x∈{t,r}分别代表发射和接收天线,J0(·)表示第一类零阶贝塞尔函数。在本文假设dt=dr=d。

图4给出了Nr=1,每个RB的n=4,R=1.78 bit/(s·Hz-1)时,采用8QAM调制,旋转角为π/8的TDA-QSFIM算法和采用4QAM调制的QSFIM算法以及MIMO-OFDM-IM算法在d=0.3的瑞利相关衰落信道上采用ML检测的性能曲线。图5给出了接收天线数为1,每个RB的Nr=1,每个RB的n=8,R=2.22 bit/(s·Hz-1)时,采用8QAM调制,旋转角为3π/8的TDA-QSFIM算法和采用4QAM调制的QSFIM算法在d=0.3的相关瑞利衰落信道上经ML检测的性能曲线。从图4和图5中也可以看出在相关信道中,TDA-QSFIM算法由于可获得二阶发射分集依然比QSFIM算法具有更好的误比特率性能,而且在高信噪比时,也比MIMO-OFDM-IM算法具有更好的误比特率性能,当BER=10-3时,TDA-QSFIM算法比QSFIM算法具有大约5 dB的性能增益。

图4 R=1.78 bit/(s·Hz-1)、Nr=1、n=4时d=0.3的相关瑞利衰落信道上3种算法的BER性能比较

图5 R=2.22 bit/(s·Hz-1)、Nr=1、n=8时d=0.3的相关瑞利衰落信道上TDA-QSFIM与QSFIM算法的BER性能比较

为了比较发射分集对TDA-QSFIM算法的影响,图6给出了Nr=2,每个RB的n=4,R=1.78 bit/(s·Hz-1)时,在独立同分布瑞利衰落信道上采用8QAM调制,旋转角为π/8的TDA-QSFIM算法和采用8QAM调制的OFDM-ISIM算法均采用ML检测的仿真性能曲线。由图可见,TDA-QSFIM算法在信噪比较大的情况下,其误比特率性能要远远好于OFDM-ISIM算法,当误比特率为10-3时,TDA-QSFIM算法相比OFDM-ISIM算法就已经具有大约6 dB的性能增益,这是因为OFDM-ISIM仅仅增大了信号点之间的欧式距离,而其采用单根发射天线并未获得发射分集,而本文所提的TDA-QSFIM获得了二阶的发射分集算法。

图6 R=1.78 bit/(s·Hz-1)、Nr=2、n=4时TDA-QSFIM与OFDM-ISIM算法的BER性能比较

4 结 论

本文提出了一种能够获得发射分集的正交空频索引调制传输算法,简称为TDA-QSFIM算法。该算法将两个调制符号进行关联构造了对角空频码,并扩展为同相和正交分量后再经不同的空频索引调制后放在RB的不同位置上,最后将同相和正交部分合并后进行发送。由于本算法对每一个RB都进行了有效的码字设计,因此获得了二阶发射分集,进而获得比现有的QSFIM算法和MIMO-OFDM-IM算法更好的误比特率性能。仿真结果进一步验证了理论分析的正确性和本文所提出的TDA-QSFIM算法的性能优越性。