采用多变量耦合网络与变分图自编码器的机械设备异常检测方法
张聪,朱永生,杨敏燕,任智军,闫柯,洪军
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
近年来,随着复杂机电装备自动化程度和信息集成度的日益提高,设备运行状态数据量激增,数据驱动的异常检测方法成为工业领域设备及零部件状态识别新趋势,为解决传统异常检测方法经验依赖性强、准确率低、误判漏检率高等问题提供了有效途径[1]。
以汽轮机、风电装备等典型转子系统为例,作为一种零部件间高度关联、高度耦合的分布式复杂系统,其运行过程中各测点振动、温度、压力等信息要素共同构成了转子系统中复杂且普遍存在的耦合关系[2]。同时,系统配备的分布式控制系统(DCS)、汽轮机监测系统(TSI)和数据采集与监视控制系统(SCADA)等所采集的数据,表现出多源、海量、异常缺乏、无标签等特点[3],给复杂系统的异常检测及故障诊断带来了极大的挑战。在复杂机电装备异常检测及故障诊断方面,刘国斌利用汽轮机DCS数据,提出了基于多传感器信息融合的神经网络方法,并开展了汽轮机故障诊断研究[4]。Niklas等针对风电机组SCADA系统监测数据,提出了一种基于自动编码器模型,通过重构所有输入信号,实现了对风电机组各组件的异常检测[5]。赵洪山等提出了一种基于风电机组主轴承SCADA状态监测数据逐层编码网络的深度学习方法[6],利用受限玻尔兹曼机逐层智能学习主轴承样本数据蕴含的特定规则,进而实现状态识别。刘超等基于风电机SCADA数据,提出了一种用于风力涡轮机状态的无监督异常检测方法,应用时空模式网络(STPN)来提取系统中变量的时空特征,然后使用基于能量的受限玻尔兹曼机(RBM)进行异常检测[7]。
上述研究均未考虑系统各监测变量间存在的复杂耦合关系,局限于利用单一变量或多变量简单叠加进行异常检测或故障识别,对系统运行状态敏感性低,计算结果的可靠性难以满足工业时序数据异常检测的需求。针对上述问题,杜海峰等利用网络表示故障数据结构,以压缩机组故障样本作为网络节点,不同样本间的相似性度量作为边,构建复杂网络,通过网络结构反映故障状态及其特征,通过对网络社群结构特性及模块性指标进行分析,建立了系统状态划分准则,实现了对系统故障的有效诊断[8]。姜洪权等通过对田纳西-伊斯曼(TE)化工系统进行抽象,并构建复杂网络,基于网络最短路径长度定义系统脆性系数,从而实现对复杂系统结构脆弱性的评价[9]。Wang等采用有限穿越可视图的方式构建复杂机电系统网络模型,并基于度分布等复杂网络统计特性,定义网络差异度系数,从而识别机电系统的[10]不同状态。冯龙飞等提出了一种基于去趋势交叉分析-网络结构熵(DCCA-NSEn)的复杂机电系统多变量耦合网络建模与状态评估的方法[11],构建了反映多变量耦合关系的加权网络模型,分析耦合关系网络的结构熵,实现异常状态检测。以上方法考虑了系统的整体性和监测数据间存在的复杂耦合关系,但多采用人为提取特征指标的方式进行异常状态检测和故障识别,依赖经验性强。
针对上述方法的不足,结合复杂机电装备各部件关联性强、监测点位多、变量耦合关系繁杂的特点,本文提出了一种基于多变量耦合网络与变分图自编码器的异常检测方法。该方法首先基于海量多源传感器正常监测数据,构建复杂系统多变量耦合关系网络,深度挖掘系统变量间的关联关系,提升复杂设备状态感知的敏感性;其次,建立变分图自编码器模型,以变量间耦合关系为输入,自适应提取关系特征,实现多源数据与系统状态的非线性映射,提升复杂装备状态识别能力;最后,以变分图自编码器模型的重建概率作为指标,判断机电系统运行状态。
1 机械设备运行状态异常检测方法
针对复杂机械系统监测数据多源、海量、异常缺乏、无标签等特点,建立基于多变量耦合网络与变分图自编码器的异常检测方法,主要由耦合网络构建及变分图自编码器构建两部分组成。其中,前者基于去趋势互相关分析(DCCA)[12],结合监测变量非线性、非平稳性及长程相关性等特性,对系统任意两变量间的关联关系进行定量分析,得到系统变量间耦合关系矩阵;后者基于变分图自编码器建立多变量耦合关系重构模型,自适应提取蕴藏在关系矩阵中的机械设备状态特性,使用重建概率作为异常分数,通过训练确定重建概率阈值,实现设备运行状态异常检测。
1.1 基于DCCA的多变量耦合关系网络构建
1.1.1 去趋势互相关分析 对于系统监测变量相互耦合、众多繁杂,且具有非平稳、非线性的特点,目前基于物理或数学模型的耦合关系分析方法已不适用,因此本文采用基于非平稳非线性序列的DCCA方法,通过计算序列去趋势协方差以最小化外部趋势,进而实现序列间相关性的分析。DCCA方法的主要流程如下[13]。

(1)

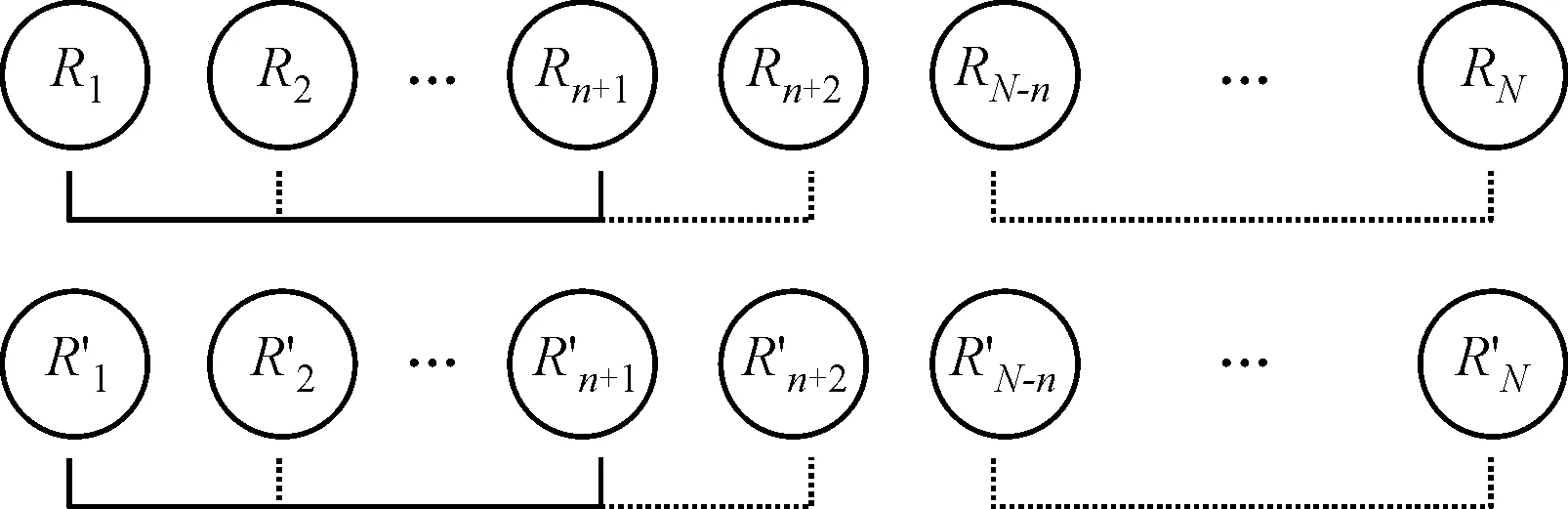
图1 集成序列划分过程
(3)计算所有区域对应的去趋势协方差
(2)
(3)
(4)重复上述分析流程,得到在不同标度时对应的波动函数,当两个序列具有明显的长相关性时,去趋势协方差函数与标度n满足
Fdcca(n)~nh
(4)
(5)
式中:h为DCCA标度指数,即两序列间耦合特征,衡量两序列间的耦合强度;Rdcca为去趋势互相关函数。
1.1.2 系统多变量耦合关系网络构建 基于去趋势互相关分析,可以得到两变量之间相关关系,而复杂机电设备监测点位众多、监测量丰富,可以同时获得多维时间序列。因此,利用去趋势互相关分析可以构建多变量间的相关关系,深度挖掘复杂系统的耦合形态。系统多变量耦合关系网络构建流程如下。
(1)以窗口宽度T截取监测系统各变量时序数据,构建m维等长时间序列集合X={x1,x2,x3,…,xm},其中xm表示第m维监测变量,基于DCCA分析分别计算集合中两两变量之间的标度指数
h11=Rdcca(x1,x1),
h12=Rdcca(x1,x2),…,hmm=Rdcca(xm,xm)
式中:hmm为两变量间的DCCA标度指数。
(2)按照DCCA标度指数下标进行排列,得到DCCA标度指数对称方阵,用A表示
(6)
式中:hij为变量xi和xj的DCCA标度指数。
(3)以长度为T的时间序列X作为节点,以DCCA标度系数对称矩阵A为边,构建耦合关系网络,如图10所示,网络表示为G=(X,A)。
1.2 基于变分图自编码器(VGAE)的异常检测模型
1.2.1 变分图自编码器构建 由于变量本身及相互间耦合关系的复杂性,系统变量的属性发生改变,关系网络G表现出典型的非结构化,该类型数据也称图结构数据,因此传统的针对结构化数据开发的深度学习模型不再适用。变分图自编码器是一种将变分自编码器迁移到图领域的无监督学习方法[14],以图结构数据作为输入,学习图的潜在表示,从而实现图的重构,如图2所示。
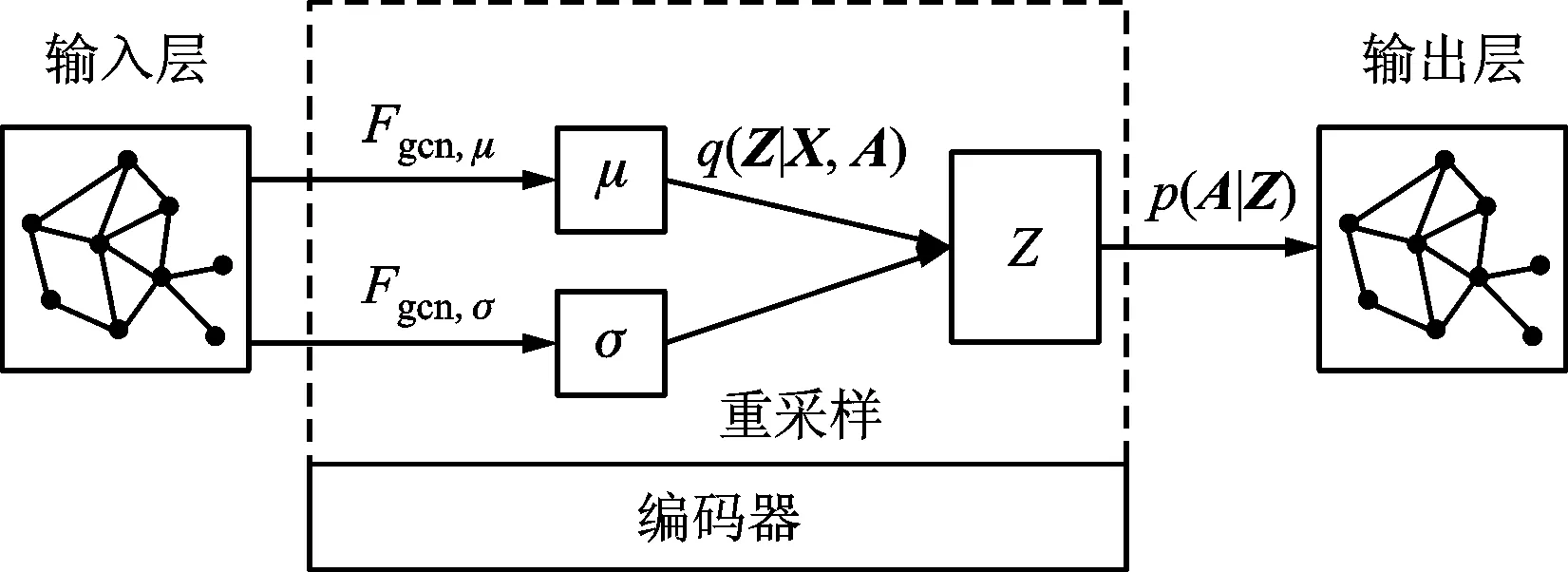
μ—均值;σ—方差;Z—潜在向量;X—节点特征;A—邻接矩阵;q—后验分布;p—先验分布;Fgcn,σ、Fgcn,μ—均值和方差的图卷积函数。
在变分图自编码器中,给定节点特征X和邻接矩阵A,首先通过图卷积网络GCN学习数据分布,并从该分布中采样得到潜在向量Z,从而学习图的潜在表示,以充分考虑到样本潜在空间的可变性,扩展模型的表现力,这个过程称为编码。利用潜在向量Z通过内积重构出原始图,这个过程称为解码。编码和解码的详细过程描述如下。
(1)编码过程。给定系统多变量关系网络G,首先利用图卷积网络学习其所属分布,本文采用两层GCN作为编码器学习目标分布,并采样得到潜在向量Z。图卷积网络的结构如图3所示。

图3 图卷积网络结构
模型假设目标为高斯分布,可以唯一地由二阶矩确定,因此在变分图自编码模型中利用GCN来计算目标分布的均值和方差
(7)
(8)
μ=Fgcn(X,A)
(9)
logσ=Fgcn,σ(X,A)
(10)

Fgcn,μ和Fgcn,σ分别为均值和方差的GCN函数,共享第1层参数W0,第2层参数W1不共享,使用下标区分。
通过均值和方差确定G(X,A)的后验分布g(Z|X,A)
(11)
(12)
式中:zi为潜在向量Z的元素。
(2)解码过程。从编码器获取的分布中采样得到的潜在变量内积作为解码器,激活函数通常选用Sigmoid,通过计算概率实现重构,过程表示为
(13)
(14)
(3)模型学习。变分图自编码器希望重构图与原始图尽可能相似的同时,GCN计算的分布与标准高斯分布尽可能相似。因此,损失函数由交叉熵和KL散度H两部分构成,交叉熵用于衡量自编码器的重构相似性,H用于衡量两个分布之间的相似性
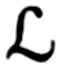
(15)
通过执行重参数化技巧[15]和批量梯度下降,完成异常检测模型训练。
1.2.2 基于重建概率的异常检测 变分图自编码器计算从学习到的分布中产生原始数据的概率,称为重建概率R,计算公式如下
R=Eq(Z|X,A)[logp(A|Z)]
(16)
通过分析重建概率的变化趋势或突变程度,实现对系统的异常检测。考虑到系统正常运行状态下重建概率较大,且具有较小的波动性,采用指数加权移动平均值[16]设定阈值,具有较高的敏感性,可有效检测重建概率的波动过程。
指数加权移动平均值(EWMA)的统计量为
lt=λR+(1-λ)lt-1
(17)
式中:t为时间;λ为历史R对当前EWMA统计量的权重,λ∈(0,1],基于研究分析该过程中取λ=0.2;l0为某段监测时间内R的均值。
EWMA统计量的均值和方差可通过下式确定
μlt=μR
(18)
(19)
系统的EWMA控制图基于时间t的下限函数为
(20)
式中:μR为训练集重建概率R的均值;σR为训练集R的标准差;ns为采样长度;z取2。
从式(20)可以看出,当t增大时,(1-λ)2t将收敛到0,下限将稳定到一个固定值,因此使用下式计算该固定值作为阈值
(21)
当测试样本的重建概率Rt 本文所提异常检测方法,通过建立系统不同传感器产生的多维度多状态监测变量间的耦合关系网络,挖掘多维时间序列间的相关关系。进一步引入变分图自编码器,使用正常数据训练模型,能够提取耦合关系网络的重要特征,并确定重建概率阈值,使用重建概率作为异常分数从而实现半监督的异常检测,算法流程如图4所示。 图4 基于耦合网络的VGAE异常检测流程图 所提异常检测方法主要步骤如下。 (1)数据归一化。DCS系统所采集的数据数量级各异,会给分析系统状态带来较大影响,因而需对监测数据进行归一化处理,公式如下 (22) (2)基于历史正常数据的系统多变量耦合网络构建。选取合适的窗口宽度T和步长S,以窗口宽度T截取时间序列X={x1,x2,x3,…,xm},按照1.1方法计算两两变量之间的DCCA标度指数,以步长S进行滑动,得出一系列DCCA标度系数对称矩阵,完成系统多变量间的耦合关系网络构建。 (3)基于变分图自编码器的异常检测模型构建。利用正常数据建立的耦合关系网络训练变分图自编码器,模型学习输入样本分布的均值和方差参数,并计算重建概率和EWMA阈值。 (4)异常检测模型应用。使用实时监测数据作为测试样本,构建耦合关系网络,输入训练阶段训练好的模型得到测试样本重建概率,当测试样本的重建概率Rt 采用某火力发电厂汽轮机组转子系统DCS多源监测数据,对所提异常检测方法进行验证,并对方法中关键参数进行研究,为方法的应用提供理论指导。 该转子系统DCS多源监测数据共包含33组时间序列,涵盖振动、温度、压力等多种物理量。由于各物理量所在测点存在冗余,剔除同一类型传感器同一位置不同测点的监测变量;同时由于DCS系统所采集的振动数据采样率低,无法准确反映设备状态,在进行多源数据融合时将其剔除,最终保留其中17组状态变量进行转子系统运行状态识别。所选变量的详细信息如表1所示,各变量所在测点位置如图5所示。 表1 汽轮机转子系统监测变量表 A—主油泵;B—高压缸;C—中压缸;D—低压缸;E—低压缸;F—联轴冷却器;G—发电机;H—集电环;0~16—含义见表1。 该转子系统于2017年5月12日出现异常,经过紧急维修,系统又持续运行24 d,之后进行了停机检修,恢复至正常状态。因此,本文选取该转子系统2月10日至6月18日的监测数据进行相关验证。 2.2.1 评价指标 在进行异常检测或故障诊断时,不希望模型将设备正常状态判断为异常状态(假阴性)或将异常状态判断为正常状态(假阳性)。传统的准确率是对模型总体性能的衡量,不能凸显异常检测对假阴性以及假阳性的关注。因此,本文选用接受者操作特征曲线下面积[17]作为评价指标,衡量模型的有效性,称为AUC概率。接受者操作特征曲线(ROC)横坐标为假阳率,纵坐标为真阳率,模型的性能越好所对应的假阳率越低,真阳率越高,即其曲线下面积越大。通过混淆矩阵对检测结果进行分类,如表2所示。 表2 混淆矩阵 根据混淆矩阵可以计算得假阳率FPR和真阳率TPR为 (23) (24) 2.2.2 模型参数设置 本文所提异常检测方法共有3个参数,分别为时序数据截取窗口宽度T,时序数据截取窗口滑动长度S,以及变分图自编码器嵌入维数D。其中,时序数据截取窗口滑动长度S决定着所提方法的最小检测间隔时间,为及时发现转子系统异常状态,选择每次滑动10个数据点进行检测,即每隔10 min进行一次系统运行状态的识别;时序数据截取窗口宽度T决定着去趋势互相关分析中两变量的长度,对分析两变量间的相关关系至关重要。本文考虑火电厂的日工作特性,选取720、1 440、2 160、2 880的数据长度进行对照分析,对照结果如图6所示。选择每次截取24 h数据(每隔1 min采集一个数据点,截取数据量为1 440)以生成所需多变量耦合关系数据效果最佳;变分图自编码器嵌入维数D决定着变分图自编码器的特征提取能力,维度太低特征提取能力不足,维度太高容易出现过拟合问题,因此需对该参数进行寻优。 图6 不同窗口宽度T的平均性能 以火电厂汽轮机转子系统2017年2月至4月的正常状态数据为训练样本,训练本文提出的异常检测模型;以5月至7月既包含正常状态又包含异常状态的数据为验证集,验证训练好的异常检测模型。按照文献[18]中的方式初始化权重,使用Adam[19]训练200次迭代,学习率设为0.01。变分图自编码器嵌入维数D对模型性能影响规律如图7所示。从图7可以发现,当变分图自编码器嵌入维数为32时,本文方法获得了最佳性能,因此后续均以32作为变分图自编码器的嵌入维数。 图7 不同嵌入维度的平均性能 2.2.3 汽轮机运行状态检测结果 以2.2.2节所述参数设置及实验方案,对本文方法的检测效果展开研究。本文方法以模型重建概率为指标判断设备的运行状态,利用式(6)得到多变量耦合网络,进而根据式(9)~(14)对模型进行训练,仅使用正常数据训练时,模型的重建概率及所对应阈值分别由式(16)和式(21)计算得出,计算结果如图8所示。从图中可以看出,随设备运行状态的波动,模型重建概率也随之波动,但均高于对应阈值,因此模型判断此时设备处于正常状态。利用测试数据对该模型进行验证,同样根据式(16),得到模型在测试数据集上的重建概率如图9所示。当设备运行处于正常状态时,监测数据的重建概率在阈值以上波动;当设备异常时,即5月12日,监测数据的重建概率发生突变,之后的24 d内重构概率均处于EWMA阈值以下;当设备大修之后,监测数据的重构概率逐渐恢复,意味着转子系统正常运行。 图8 训练集重建概率R及EWMA阈值控制图 图9 测试集重建概率R及EWMA阈值控制图 耦合关系网络作为本文方法的关键,一方面可以挖掘复杂监测系统各监测变量的关联关系,摆脱传统方法仅对单一数据进行建模,检测灵敏度低的困境;另一方面又可以为变分自编码器提供良好的输入,便于建立数据与状态的映射关系。利用2.2.2节的时序数据截取窗口宽度T和时序数据截取窗口滑动长度S,分析转子系统正常状态和异常状态下的耦合网络,结果如图10所示。图中数字节点表示汽轮机转子系统监测变量,节点间的连线代表DCCA矩阵各元素的值,表征两变量间耦合关系大小,节点间无连线说明两变量间无耦合。当设备均处于正常(或异常)状态时,各时刻耦合网络存在差异性(横向比较),说明单纯依靠数值判断无法准确确定设备的运行状态,仍需进一步提取耦合关系特征进行状态识别;当设备由正常状态转为异常状态时,监测变量耦合关系发生了较状态内部差异更为显著的变化。例如,当设备处于正常状态,变量0、变量12、变量15与其他变量均没有关联关系;当设备处于异常状态时,变量0、变量12、变量15与其他变量产生了关联关系,说明耦合关系网络能够很好地捕捉设备状态变化。 (a)正常状态下耦合关系网络 2.2.4 方法对比 为验证本文方法的先进性,本节引入5种常用的无监督学习模型进行对比,模型分别为图自编码器(GAE)[14]、卷积变分自编码器(CVAE)[21]、卷积自编码器(CAE)[20]、变分自编码器(VAE)[6]以及自编码器(AE)[5]。由于5种模型的输入特性不同,因此上述5种模型的输入分别对应为原始状态向量、原始状态向量、耦合关系矩阵、耦合关系矩阵、原始状态向量+耦合关系矩阵。此外,构建多变量间的耦合关系除可采用去趋势互相关分析外,文献[14]还提出基于图结构数据的0和1邻接矩阵建立变量间的关联关系,但其只能定性表征节点间的相关关系,本文也将对其进行比较。为了避免实验中的随机性,每组实验重复5次,平均结果如图11所示,其中A和X作为模型的输入,分别表示邻接矩阵和特征矩阵。 从图11可以看出,本文所提方法异常检测结果优于其他方法或输入的检测结果。由图11a可以看出,包含变量及变量间关联关系的方法检测准确率明显高于仅含一种输入的方法,变分图自编码器因引入图卷积网络作为编码层,实现对图数据的特征提取,效果明显优于传统方法,且变分图自编码模型的特征提取能力优于基于重建误差的图自编码器。由图11b可以看出,相较于文献[14]所提利用邻接矩阵表示变量间相关关系,去趋势互相关分析通过计算两两变量间的去趋势互相关进而构成耦合网络,定量表征了复杂系统多源状态间的耦合性,能够更加准确地表示变量间的耦合关系。 (a)算法 本文提出了一种基于多变量耦合网络的变分图自编码模型,实现汽轮机转子系统异常检测。针对汽轮机组多维多态监测数据,采用去趋势互相关分析(DCCA)方法,对多维变量间的相关关系进行定量分析,构建系统多变量耦合关系网络;进一步建立变分图自编码模型,对系统多变量耦合关系网络进行节点嵌入和特征提取。模型使用图卷积网络学习输入数据的分布,采样获得其潜在表示,实现耦合网络的重构,采用重建概率作为异常分数,通过正常状态的耦合网络训练所得模型,对测试数据进行异常检测。 实验结果表明:与人为建立多变量耦合关系网络特征指标进行异常检测的方法相比,本文方法通过建立变分图自编码模型,自适应提取耦合网络的深层特征,减少了人为因素和先验知识的影响,检测结果更客观准确;与直接使用原始多维状态变量作为模型输入的深度学习方法相比,本文方法通过建立多维变量间的耦合关系,能更准确地挖掘机组出现异常前状态参数间相关关系的变化。该方法可应用于工程实际中汽轮机组转子系统状态异常检测。1.3 基于DCCA-VGAE的异常检测方法

2 实例验证
2.1 数据描述

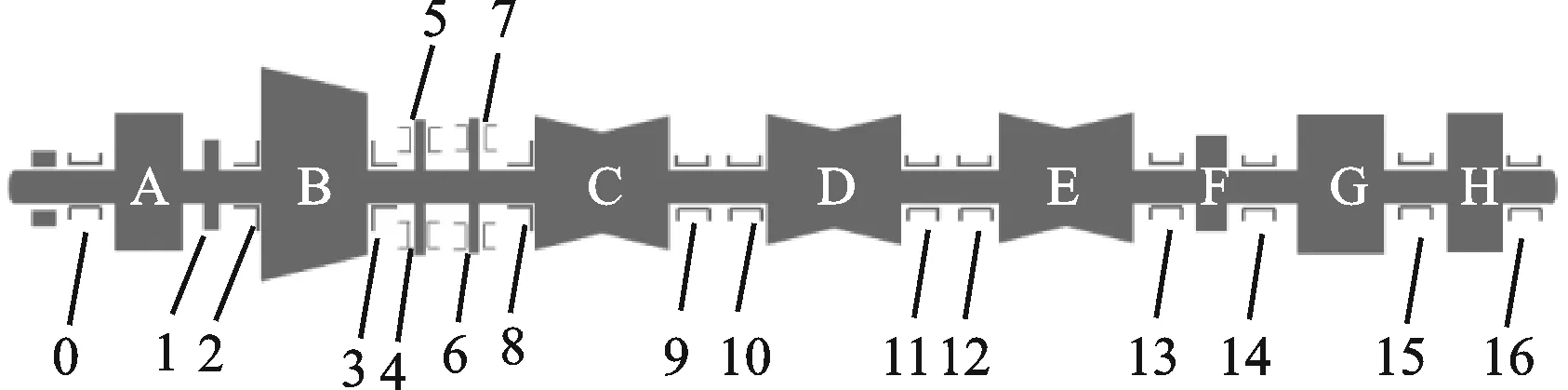
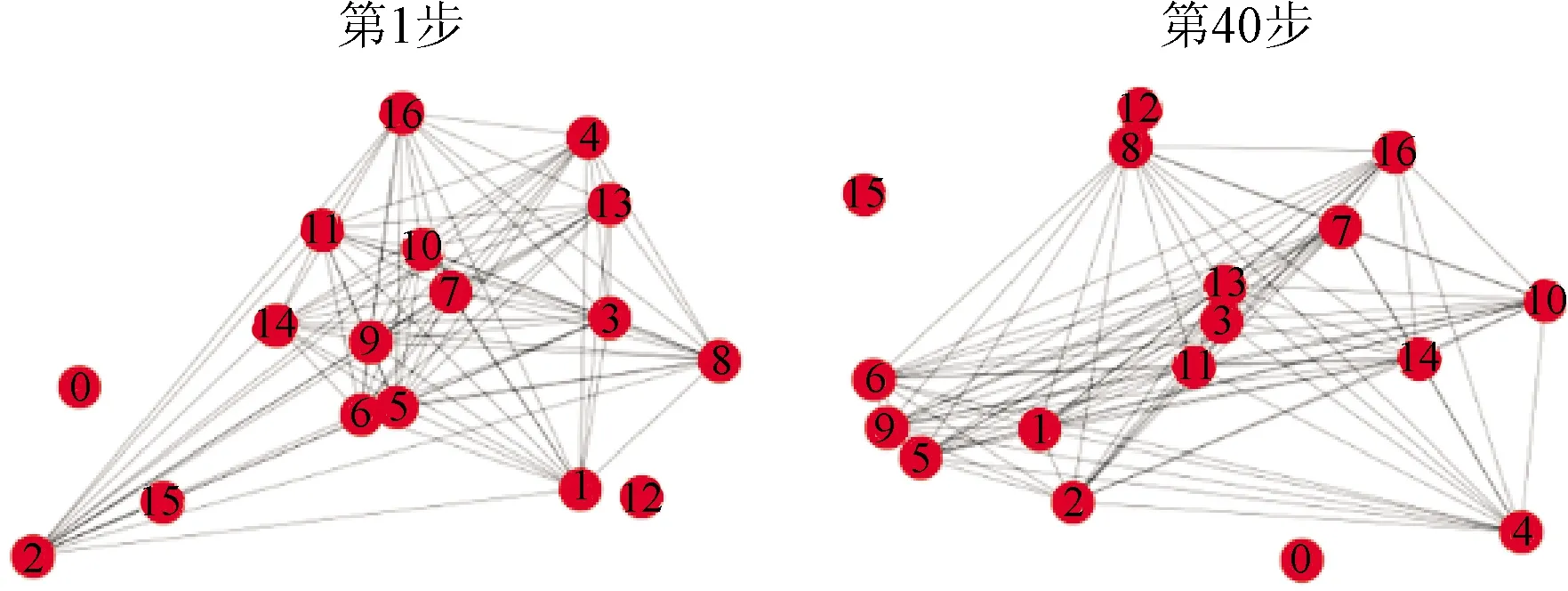
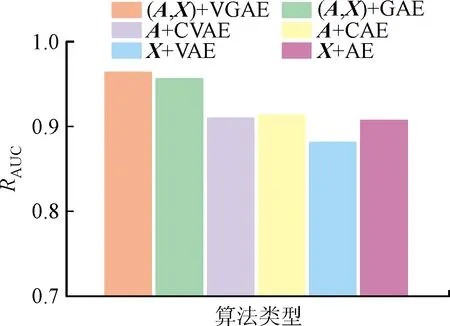
2.2 汽轮机运行状态检测结果分析

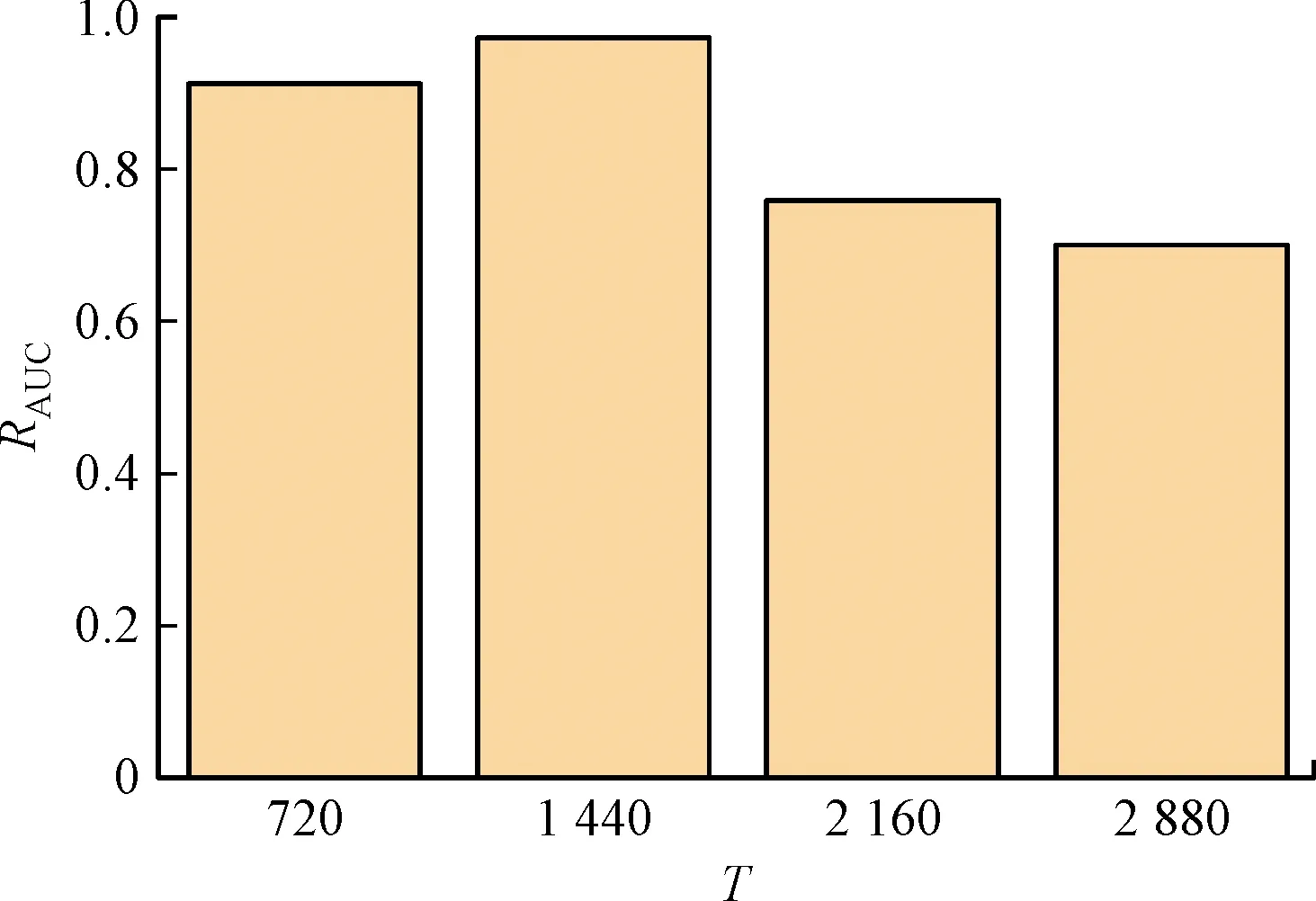



3 结 论

