面向双关节机械臂的参数可调RBF神经网络控制

刘凌，李志成，张莹

(1.西安交通大学电力设备电气绝缘国家重点实验室，710049，西安；2.西安交通大学电气工程学院，710049，西安)

随着机械臂系统在生产生活中的应用范围越来越广,机械臂系统的控制精度和控制稳定性要求也越来越高。目前机械臂已经广泛地应用在机械制造[1]、交通运输[2]、农业生产[3]、航空航天[4]、医疗卫生[5]等领域。由于机械臂要完成的任务很复杂,所以单关节机械臂难以实现这些操作,很多操作是需要多关节机械臂来完成的。多关节机械臂是一个非线性,强耦合的系统[6],机械臂控制问题的目标是将机械臂的终端稳定、准确地控制到其期望的位置,由于其运行时工作环境的变化而受到外界不确定因素的扰动以及负载的变化,都会加大机械臂控制的难度。

近年来国内外众多学者在机械臂的控制方面做了很多研究。在机器人机械臂控制算法上有滑模控制[7-9]、自适应控制[10-12]、PID控制[13-14]、神经网络控制[15-17]等。由于神经网络有很好的非线性逼近能力,而且神经网络控制所需条件较少,所以神经网络在机器人控制方面应用很广泛。运用RBF神经网络控制有达到稳定所需时间较长,运行初始阶段误差较大等缺点。很多学者对这些情况进行了优化。文献[18]采用了RBF神经网络估计器和观测器对系统的不确定性进行估计,从而达到对神经网络权值进行更新的目的,提高了对机械臂动力学不确定部分的补偿作用。文献[19]设计了新型鲁棒项来调节神经网络的权值并补偿控制过程中的未知项,改善了神经网络对系统结构发生变化时对未知部分的补偿效果。文献[20]提出了一种利用熵聚类的方法对RBF神经网络的基函数中心值进行计算,避免了传统算法中使用K均值方法的重复迭代过程并通过梯度下降法调整神经网络传递权值,提高了快速性和准确性。

为了克服神经网络参数固定所带来的初始运行误差大、达到稳定状态所需时间长的问题,本文提出了一种参数可调的RBF神经网络算法对双关节机械臂模型的控制误差进行补偿。设计了一种模糊控制器对双关节的输出控制力矩进行补偿,使经过调整后的力矩可以更好地逼近实际控制力矩。数值仿真结果表明,本文提出的方法可以有效地减小机械臂初始运行时的误差幅值和系统达到稳定的时间。

1 多关节机械臂系统动力学模型

针对n关节刚性机械臂,考虑摩擦力和外加扰动,其动力学方程可以表示为

(1)

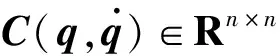
为了使机械臂的实际位置更快更好地趋近于理想位置。针对双关节机械臂轨迹控制中误差逼近过程初始误差大的缺陷,本文提出一种改进型RBF神经网络控制方法,网络的中心以及鲁棒项中的补偿环节可以根据实际误差的大小来调节自身的参数进而实现轨迹跟踪。

双关节刚性机械臂示意图如图1所示。图中l1为连杆1的长度,l2为连杆2的长度。m1为连杆1的质量,m2为连杆2的质量。q1和q2分别是关节1和关节2的位置角。

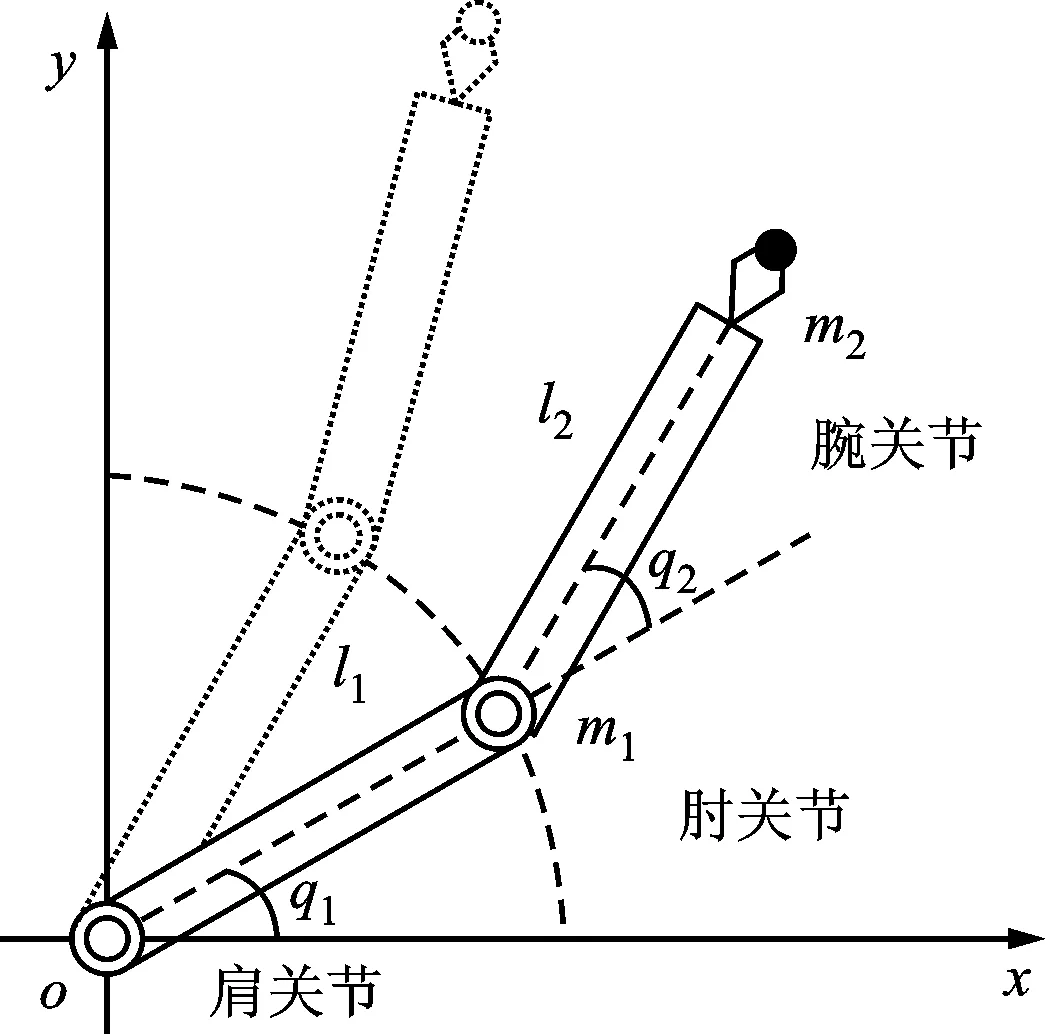
图1 机械臂结构

2 改进型RBF神经网络控制算法

2.1 改进型径向基(RBF)控制器设计

对于n关节机械臂由于模型不确定项带来的误差f(x)采用RBF网络进行逼近。定义RBF网络函数

(2)

f(x)=WTφ(x)+μ

(3)

式中:x为神经网络的输入信号;W为神经网络的权值向量;φ(x)为神经网络中间层的输出向量;μ为神经网络的逼近误差;ci是RBF神经网络第i个中间神经元的中心值向量;b是中间神经元函数宽度。

跟踪误差定义为

e(t)=qd(t)-q(t)

(4)

式中:qd为机械臂运动的理想位置角轨迹;e=[e1,e2,…,en]T。误差函数定义为

(5)

式中:r=[r1,r2,…,rn]T;Λ=ΛT且为正定矩阵。机械臂速度定义为

(6)

将式(6)代入式(1)并整理得

G+F+τd-τ=-Cr-τ+f(x)+τd

(7)

式中

(8)

取神经网络的输入为

控制率设计为

(9)

将控制率(9)代入到式(7)得

(10)

考虑存在神经网络的逼近误差和外加未知干扰存在的情况,设计了一种参数可调的鲁棒项h=kuo。其中k是一个正的常数。uo=[uo1,uo2,…,uon]T是补偿器的输出。

设计Lyapunov函数为

(11)

对式(11)求导并将式(10)代入得

(12)

(13)

(14)

rT(μ+τd+h)=rT(μ+τd+ku0)≤0

(15)

2.2 基于遗传算法的网络中心参数自寻优

RBF神经网络在控制机械臂系统运行的过程中,其参数b的选取对系统的控制稳定性影响较大,本文通过遗传算法确定了该参数的最优值。本文首先选取7个不同的b值进行测试,得到了7组机械臂实际位置和理想位置的误差结果。基于该结果进行拟合,得到拟合曲线。利用遗传算法对拟合得到的曲线进行参数寻优,最终得到最优的函数宽度b。机械臂关节角度误差的计算公式为

(16)

式中:E为实际位置与理想位置的误差量;H1、H2、H3、H4分别是第一关节在取得前4个实际位置波形最值时刻的误差值。

设置寻优参数:种群个体数为40,最大遗传代数为25,代沟设置为0.9。

传统的RBF神经网络多通过对权值的调整对不确定项进行逼近,使输出可以逼近不确定项,从而使控制力矩接近实际力矩。本文利用关节实际误差来调整神经网络的中心参数cj,其修正参数如下

(17)

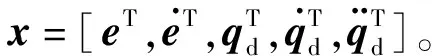
经过n次迭代的中心参数为

cj(n+1)=cj(n)+Δcj

(18)

2.3 控制力矩模糊补偿环节设计

为了补偿机械臂在运行过程中由于不确定扰动因素所带来的影响,本节采用模糊补偿环节对控制力矩进行调整。在输入参数变化范围较大时,输入参数值可能会超出模糊补偿环节的边界范围。设计伸缩因子调整模糊补偿论域的输入范围可提高控制器的有效性并对输入力矩进行有效补偿。在机械臂运行过程中,检测模块会不断测量理想轨迹与实际轨迹之间的误差,将误差和误差变化率作为模糊控制器的输入,并将模糊控制器的输出传递到转矩控制模块,对机械臂转矩参数进行定时调整。控制器的补偿原则为:

(1)当轨迹之间的误差值为正的较大值时,关节电机的输入转矩大于理想转矩,此时需要补偿器返回一个负值来调整关节电机的实际转矩;

(2)当轨迹之间的误差值为负的较大值时,机械臂关节电机的输入转矩小于理想转矩,此时需要补偿器返回一个正的值来调整电机的实际输出转矩;

(3)当轨迹之间的误差很小的时候电机的输出转矩只需要很小地调整。

根据以上原则设计如下转矩模糊补偿器。补偿器设计为双输入单输出。二维输入为e和ec,控制器输出为uo。模糊规则是用来描述控制方法的语句,模糊化是将机械臂实际的轨迹和理想轨迹的误差e和误差变化率ec作为模糊控制器的输入。轨迹误差变化率模糊子集为{负大,负中,负小,0,正小,正中,正大}={NB,NM,NS,ZO,PS,PM,PB},模糊控制器的输出为{负大,负中,负小,0,正小,正中,正大}={NB,NM,NS,ZO,PS,PM,PB},设计模糊控制规则为49条:

(1)If(eis NB)and(ecis NB)then(uois PB);

(2)If(eis PM)and(ecis 0)then(uois NB);

⋮

(49)If(eis PB)and(ecis PB)then(uois NB)。运用上述的模糊控制器的输入输出规则可以得到模糊补偿环节的控制规则如表1所示。

表1 uo的模糊控制规则设计

对于论域固定的模糊补偿器,对n关节刚性机械臂受扰动状态下,其期望轨迹与实际轨迹之间的差值变大会超出模糊补偿器的输入范围并导致超出论域范围的部分失效,不能起到调节补偿作用。本文提出用比例因子对输入区间进行调整的策略

ein=d(e/a)

(19)

式中:a是当输入参数e大于论域区间时的最大值,表示为

(20)

d是模糊控制器的输入参数e的论域范围的最大值;ein是经过比例变换后的模糊控制器的输入参数。

参数可调的RBF神经网络控制系统框图如图2所示。

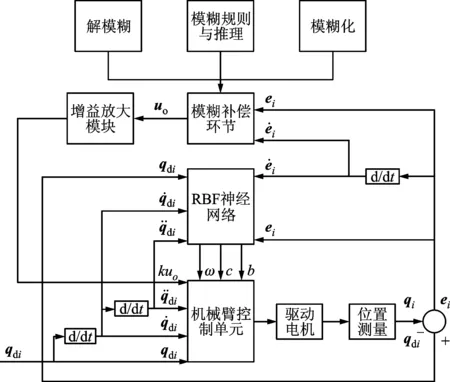
图2 控制系统整体框图

3 数值仿真

为了验证本文提出的控制方法的有效性,对双关节机械臂系统进行仿真验证。式(1)双关节机械臂动力学方程中的各参数计算公式如下

(21)

(22)

(23)

(24)

τd=[0.2sint,0.2sint]

(25)

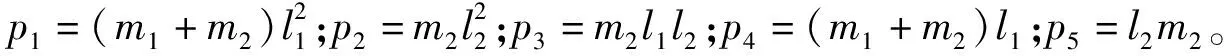
(1)对参数b的遗传算法仿真取RBF神经网络的c值为

当RBF神经网络的神经元宽度b取不同值时,根据式(16)所得对应的机械臂关节角度误差如表2所示。

表2 参数b的值以及对应的误差E

对表2中的误差结果进行函数拟合,结果如图3～图6所示。

图3 函数拟合结果图

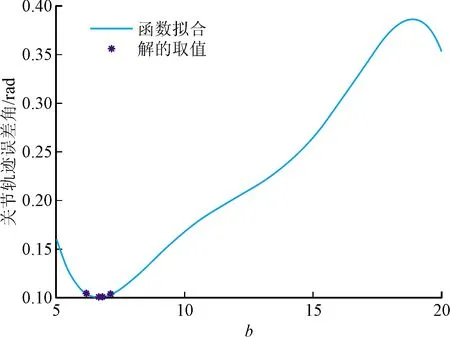
图4 参数b的遗传寻优结果

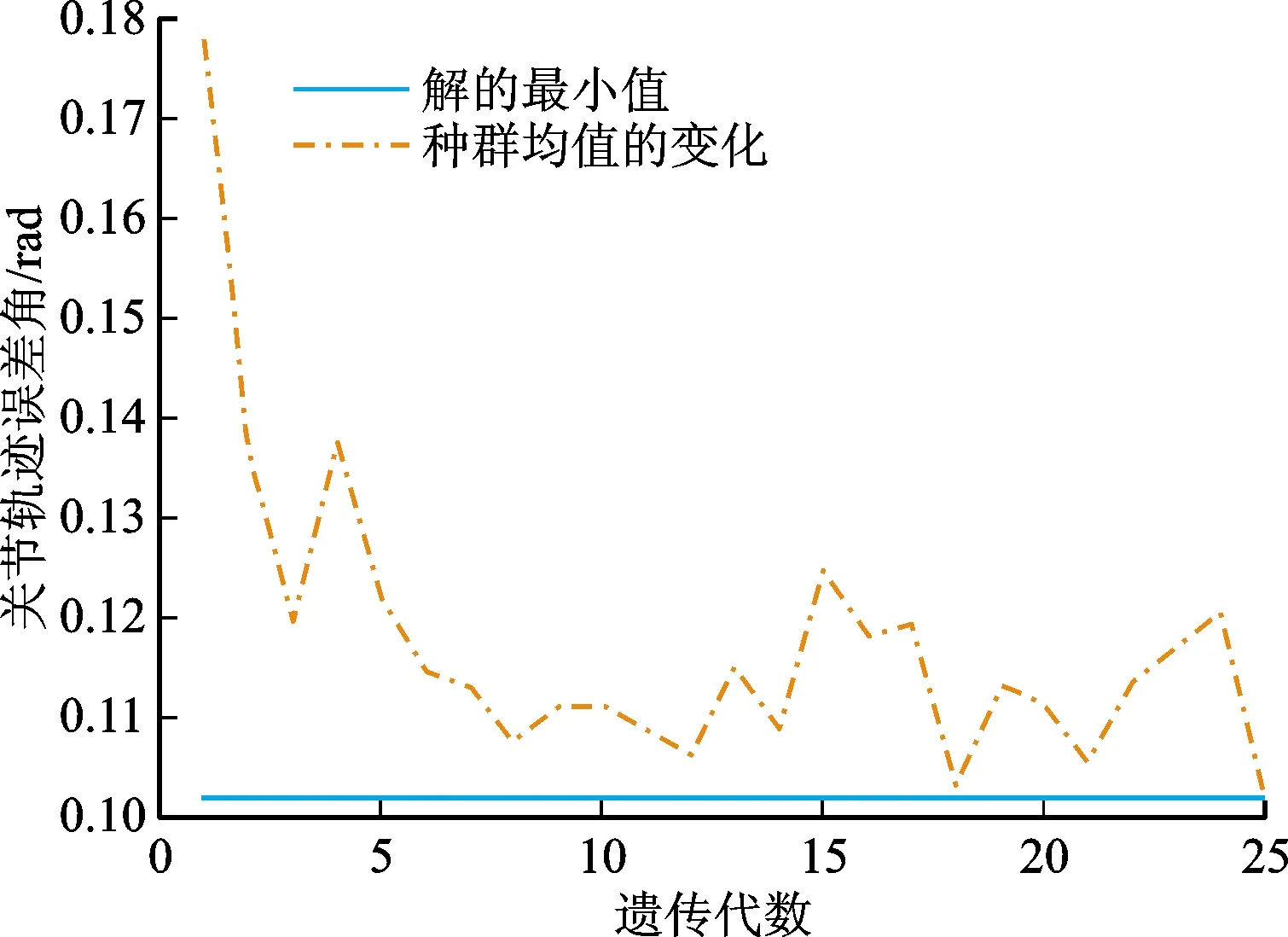
图5 关节1实际误差

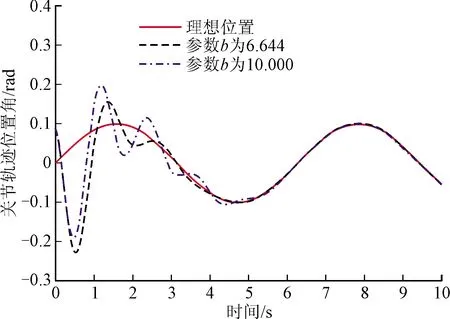
(a)关节1

通过遗传算法寻优得到的最优解b=6.643 5,E=0.102 1。

(2)利用梯度下降法对参数c的值进行调整,并采用模糊控制算法对机械臂转矩进行补偿仿真,其中RBF神经网络的高斯基函数中的参数c的初始值为

b=10。

基本模型和含模糊补偿器对比结果如图7、图8所示。

(a)关节1

(a)关节1

从图6和图7中利用参数b和c进行寻优调节的方法结果和图8中利用模糊补偿器对神经网络控制调整的结果可得出,参数调节以及模糊补偿的方法均能实现对RBF神经网络控制方法的改进,可以减小机械臂起始运行阶段实际轨迹与理想轨迹之间的误差,从而提高对期望轨迹的跟踪精度。模糊补偿器通过提取输出轨迹误差可以实时补偿机械臂控制转矩的变化需求,缩短了机械臂达到稳定的时间,说明该控制方法能够更快地逼近系统的不确定项。根据仿真结果分析,本文提出的方法不仅可以使初始运行状态快速达到稳定,而且对存在扰动的情况也可以有很好的调节效果。

4 结 论

本文面向多关节刚性机械臂设计了一种新型参数可调径向基(RBF)神经网络控制器。运用梯度下降法对RBF神经网络中心参数进行修正,实现了网络中心参数的在线优化。进一步提出了一种输入边界可以调整的模糊补偿器,使补偿后的机械臂实际轨迹更好地逼近理想轨迹。最后,采用遗传算法对RBF神经网络函数宽度值进行寻优。仿真结果表明,本文提出的参数可调整的RBF神经网络控制方法提高了机械臂控制过程中的精确性和鲁棒性,并有效地减少了轨迹跟踪的时间。