外加电磁场作用下铸锭冒口凝固过程数值模拟研究

顾 涛，李静文，张帅鑫，刘化峰，王明家，赵宇宏,*，侯 华

(1.中北大学 材料科学与工程学院，山西 太原 030051；2.中石油天然气销售分公司江西省公司，江西 南昌 330000；3.燕山大学 材料科学与工程学院，河北 秦皇岛 066004)

0 引言

铸锭是工业生产中最为常见的一种铸件产品，常作为后续产品的坯料使用，其生产质量直接影响后续产品的品质。为了保证后续产品质量，制造品质良好的铸锭十分关键和必要[1]。然而铸锭在凝固过程中，随着温度的降低会发生体积收缩，如果不能对其进行及时有效的补缩，将会出现缩孔、缩松等铸造类缺陷。工业上可以通过设计大尺寸的冒口来强化补缩效果。虽然该方法可有效解决铸锭补缩问题，但是大尺寸冒口将导致大量原材料的浪费。因此，如何在保证铸锭补缩质量的同时又能缩小冒口尺寸是铸锭生产中需要解决的一个难题。

数值模拟技术是近年来一种新兴的研究技术，被广泛应用于各个研究领域中[2-3],通过模拟计算铸造凝固过程可以协助研究者优化铸造工艺与模具设计[4-7]。例如，研究者通过对铸锭凝固过程进行数值模拟，优化了冒口设计，提高了冒口补缩效率，但是由于铸锭凝固的同时冒口本身也在传热凝固，因此这些技术作用效果十分有限[8-9]。对冒口进行加热，补偿凝固过程中该区域的热量损失，是提升冒口补缩效果的一种有效途径和方法。研究者尝试电弧加热[10]、电渣加热[11]等多种方式加热冒口,有效补偿了凝固过程中冒口的热量损失，显著延长冒口区域金属液的凝固时间，提升冒口补缩效率。除了上述外热源方式外，感应加热也是一种热源方式[12]，通过在铸锭冒口外部设置电磁感应加热装置，可以使冒口区域的熔体在电磁场作用下产生感生焦耳热，感生焦耳热可以有效补偿冒口区域在凝固过程中散失的热量[13-14]。与其他加热方式相比，冒口感应加热具有设备要求简单、加热速度快、高效环保不污染金属熔体等特点[15-16]，具有十分广阔的应用前景。

目前，有关电磁感应加热冒口技术研究还相对较少，电磁场作用下的冒口凝固补缩特征还需要进一步研究与加强。为此，本文通过ANSYS对铸锭的冒口感应加热过程进行模拟计算，研究不同电磁参数下(外加电流、频率)对冒口区域温度场分布的影响，为优化工艺参数，提升冒口补缩效率和减小冒口尺寸提供参考。

1 电磁场作用下冒口感应加热过程模拟计算

电磁感应加热利用交变磁场在工件内部产生感生电流，将感生电流产生的焦耳热作为内热源控制冒口内部温度分布，因此温度场的求解过程涉及电磁场-温度场耦合，该过程将应用Maxwell方程组与Fourier导热微分方程联合求解[17]。

1.1 电磁场计算模型

本文模拟过程中电磁场频率范围属于中低频率，近似于稳态情况，因此，可以不考虑位移电流的影响。根据中低频的电磁场模拟相关理论，在不考虑位移电流的情况下，描述电磁场的准静态Maxwell方程如下[18]：

(1)

(2)

(3)

式中，H为磁场强度，J为电流密度，B为磁感应强度，E为电场强度。

介质的磁特性本构方程如下：

H=B/(μ0·μr)，

(4)

J=σ·E，

(5)

式中，σ为电导率，μr，μ0分别为相对磁导率和绝对磁导率，μ0=4π×10-7H/m。

1.2 温度场计算

感应加热过程中，冒口在交变磁场中产生感生涡流热，将其作为冒口的外加热源，通过Fourier导热微分方程求解冒口区域的温度场分布。

铸锭内热源Qv为

(6)

结晶潜热Q1为

(7)

感生焦耳热Q2为

(8)

Qv=Q1+Q2，

(9)

式中，k为热传导系数，ρ为材料密度，Cp为比热容，t为时间，T为温度，L为凝固潜热；fs为固相率，ω为角频率，Ar和Ai分别为电流密度实部和虚部。σ为电导率。

1.3 有限元模型

1.3.1几何模型及网格划分

本文采用ANSYS软件模拟计算外加电磁参数(电流强度、电源频率)对铸锭冒口凝固过程中电磁场与温度场分布的影响规律。模拟过程选用的电流强度分别为0 A、500 A、1 000 A，电源频率为1 000 Hz、1 500 Hz、2 200 Hz、3 000 Hz。模拟过程中实体模型包括：冒口、铸锭、线圈、空气等。铸锭高度为450 mm，铸锭半径为125 mm，冒口上端和下端半径分别为90 mm和110 mm；冒口高度为120 mm；线圈共计5 匝，线圈距冒口30 mm，线圈总高度120 mm，具体结构示意图如图1(a)所示。由于电磁场特有的集肤效应，因此在铸锭及冒口表面划分了5层边界层网格保证求解精度，对铸锭和冒口之外的空气场区域，划分尺寸较大的网格单元。有限元模型的网格划分如图1所示。

图1 结构示意图和有限元模型网格划分Fig.1 Schematic structure diagram and finite element model meshing

1.3.2材料的物性参数

铸锭所用材料为铸钢ZG230-450，对应物理性能参数如下：导热系数为30 W/(m·K)，比热容为560 J/(kg·K)，固相线温度为1 676 K，液相线温度为1 788 K，结晶潜热为2.68×105J/kg，密度为7 830 kg/m3，电导率为1.1×106S/m。线圈所用材料为铜，电导率为5.8×107S/m。

1.3.3初始条件和边界条件

在电磁场模拟计算过程中，采用了Balloon边界条件，即认为磁场为开域，无限远处磁场为零[19]。有限元模型的最外层空气视为远场边界处理。在温度场模拟计算过程中，温度场的传热采用第三类边界条件[20]，模具预热温度、浇注温度、环境温度分别为573 K、1 823 K、299 K。各区域的表面换热系数如表1所示。

表1 各区域的界面换热系数Tab.1 Heat transfer coefficients of various regions

2 冒口感应加热电磁场仿真结果分析

2.1 磁感应强度分布

当电流I=1 000 A，频率f=2 200 Hz时磁感应强度在冒口轴向、径向上的分布如图2(a)与图2(b)所示。受线圈端部效应的影响，磁感应强度在冒口轴向上呈现“两端小，中间大”的分布趋势[21-22]，在高度中部区域磁场强度较大，峰值可达到53 mT。磁感应强度从冒口中心到外表面近似呈幂指数规律递增，表现出集肤效应。

图2 电流I=1 000 A，频率f=2 200 Hz时的磁感应强度分布Fig.2 Distribution of magnetic induction intensity at current I=1 000 A and frequency f=2 200 Hz

2.2 感生焦耳热的分布

图3为电流I=1 000 A，频率f=2 200 Hz时冒口区域焦耳热分布示意图。由于冒口内金属熔体感生焦耳热存在集肤效应，感生的涡流热主要集中在冒口表层区域，且由外向内逐渐减小，经计算该条件下感生焦耳热功率为6 411 W。感生焦耳热补偿冒口散热，延缓冒口内金属液凝固进程，强化冒口补缩效率。

图3 电流I=1 000 A，频率f=2 200 Hz感生焦耳热分布图Fig.3 Distribution of Joule heat at current I=1 000 A and frequency f=2 200 Hz

2.3 电流强度对磁感应强度及焦耳热的影响

图4为电源频率恒为2 200 Hz，不同电流强度下冒口径向上磁感应强度分布变化曲线。由图4可以看出，不同的电流强度下磁感应强度的分布都近似呈幂指数分布，因此电流强度的变化对冒口径向上磁感应强度的分布特征的影响不大。但是磁感应强度的峰值随着电流强度的增加有明显的增大，当电流强度是500 A时，冒口径向磁感应强度的峰值为22 mT；电流强度为1 000 A时，冒口径向磁感应强度峰值为40 mT。通过数值模拟对该条件下的感生焦耳热功率进行计算，结果表明，频率f=2 200 Hz、电流强度I=500 A时，感生焦耳热功率为1 638 W；电流强度I=1 000 A时，感生焦耳热为6 411 W。由此可知，电流强度越大，产生的感生焦耳热功率就越大。

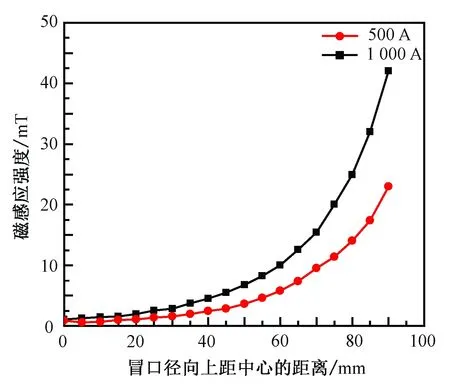
图4 电流强度对冒口径向磁场分布的影响Fig.4 Influence of current intensity on the distribution of radial magnetic field of riser

2.4 电源频率对磁感应强度及焦耳热的影响

图5(a)为电流强度恒为500 A、冒口高度为100 mm截面的径向磁感应强度分布，电源频率增大，磁感应强度峰值略有提升，但增幅不大，基本保持在25 mT左右。然而电源频率的变化会改变冒口内部电磁场分布和集肤层厚度，随着电源频率的减小，冒口区域沿径向的磁感应强度趋于平缓，集肤深度增大，具体如表2所示。图5(b)为I=1 000 A时，感生焦耳热与电流频率的关系曲线。可以看出，随着电源频率增加，感生焦耳热有所增加，在所选1 000～3 000 Hz范围内，频率由1 000 Hz增至3 000 Hz时，感生焦耳热功率由4 000 W增至7 500 W。

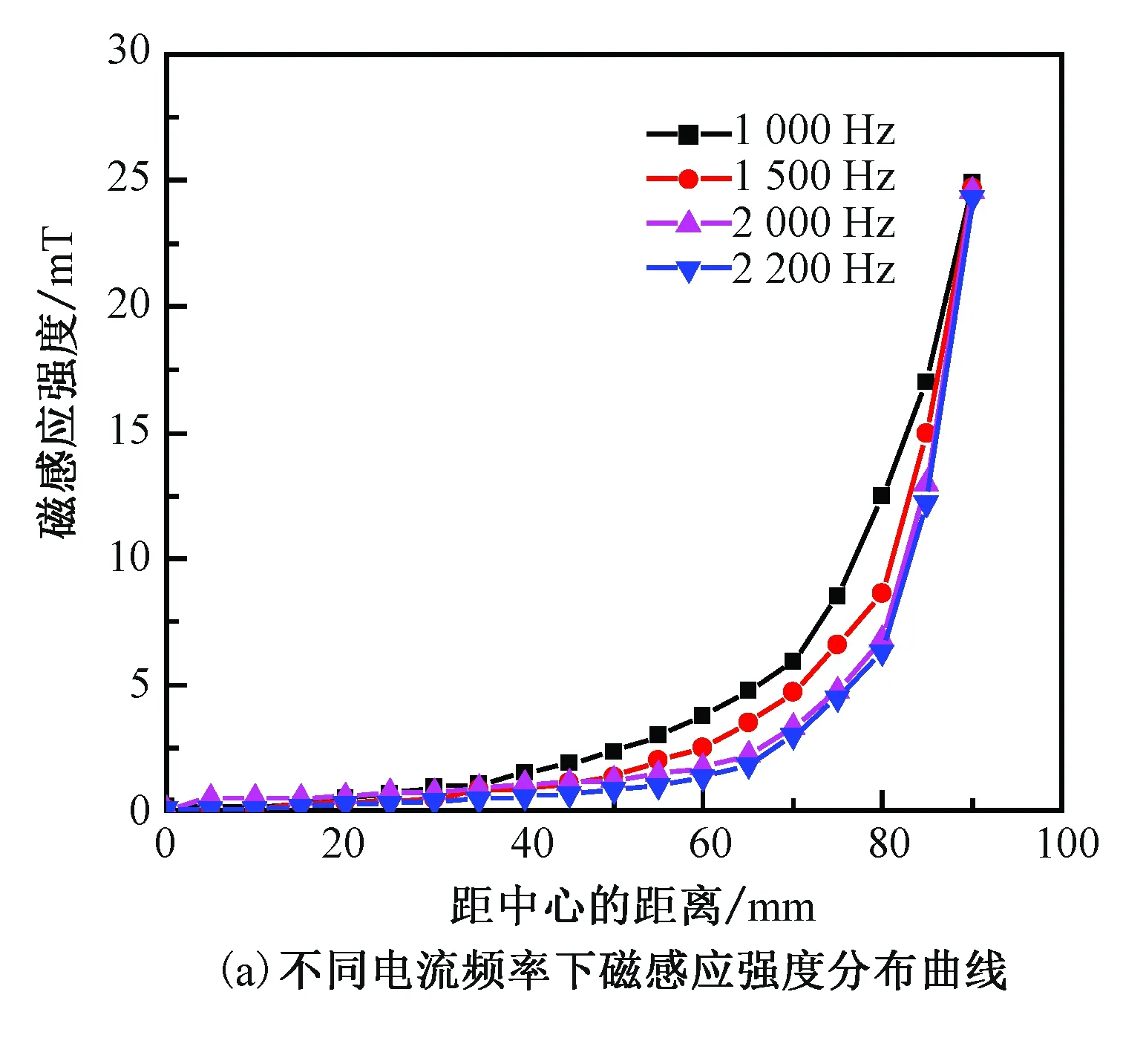
图5 电源频率对磁感应强度和感生焦耳热的影响Fig.5 Influence of power frequency on magnetic induction intensity and induced Joule heat

表2 不同电流频率下的集肤深度Tab.2 Skin depth at different current frequency

3 冒口感应加热温度场仿真结果分析

3.1 电流强度对温度场的影响

3.1.1电流强度对温度场分布的影响

图6是无感应加热条件下，铸锭在600 s、800 s、900 s、1 000 s时的温度场分布。由图6可以看出，铸锭的凝固趋势为轴向自下而上推进、径向从外表面往心部推进。800 s时，铸锭尚未完全凝固，而冒口外表面的部分金属液已开始发生凝固。1 000 s时，铸锭已完成凝固，此时冒口大部分区域已经凝固，只有中心部分残留少量的高温熔体，呈现类似“V”型的温度分布。

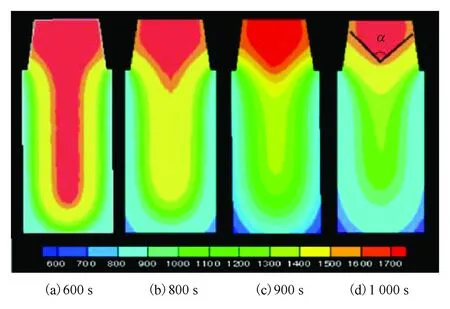
图6 无感应加热条件下不同时刻的温度场分布等值线图Fig.6 Temperature field distribution at different time during the solidification process without induction heat

图7是外加感应电流强度为1 000 A时铸锭在600 s、800 s、900 s、1 000 s时的温度场分布。将图7(b)与图6(b)相比，铸锭凝固趋势与传统凝固趋势基本相似，但不同之处在于，图7(b)冒口区域内部金属液温度下降不明显，大部分仍处于熔体状态。对比图7(d)与图6(d)发现，铸锭本体发生凝固，但冒口内部仍存在大量高温熔体(温度高于固相线1 676 K)。从凝固趋势来看，由于外加电磁场作用，产生涡流焦耳热，弥补冒口在凝固进程中所散失的热量，改善了冒口区域温度场分布，冒口的凝固趋势基本呈平面型沿轴向自下向上推进，使冒口区域的金属液较长时间地处于高温液态，这有利于实现冒口对铸锭充分补缩。

图8为不同条件下t=800 s时冒口高度75 mm截面的径向温度分布曲线。在没有感应加热条件，冒口区域径向上的温度梯度较大，温度场分布极不均匀，径向温差高达137 K，当电流强度为500 A时，感生焦耳热弥补冒口区域的热量损失，冒口径向温度梯度有所减小，温差降至102 K；当电流强度为1 000 A时，感生焦耳热增大，径向温差大幅度减小，仅有42 K，温度场沿径向分布基本均匀。

图7 1 000 A、2 200 Hz下不同时刻的温度场分布Fig.7 Distribution of temperature field with condition of 1 000 A and 2 200 Hz at different time

图8 冒口沿径向上的温度分布Fig.8 Temperature distribution in radial section of the riser

3.1.2电流强度对冒口补缩通道角的影响

图9为t=1 000 s时不同电流强度下的冒口补缩通道角变化。从末端向着冒口方向液相线之间形成的夹角φ称为补缩通道扩张角(简称补缩通道角)，根据温度场结果判定冒口的补缩通道角大小。在没有感应加热条件下冒口的补缩通道角为88 °；当电流强度为500 A时，冒口的补缩通道角为102 °；电流强度为1 000 A时，冒口补缩通道角增加至130 °。这表明感生焦耳热随电流强度的增加而增大，弥补冒口在凝固进程中所散失的热量，控制冒口区域的温度场分布，使等温线分布趋于平缓，减小径向上的温度梯度，补缩通道角增大，有利于冒口对铸锭的充分补缩，避免缩孔、缩松缺陷。

图9 不同电流强度下补缩通道角Fig.9 The angle of the feeding channel at different current intensity

3.2 电源频率对冒口补缩通道角的影响

在电流强度I=1 000 A，t=1 000 s条件下，研究了电源频率对冒口补缩通道角的影响规律。图10为不同频率下的补缩通道角变化，可以发现电源频率为1 000～2 200 Hz时，随着电源频率增大，补缩通道角由115 °增至130 °，增幅明显；电源频率为2 200～3 000 Hz时，电源频率对补缩通道角影响较小，2 200 Hz与3 000 Hz工况下仅相差2 °。这是因为在电源频率为1 000～2 200 Hz时，增大电源频率，可以增大线圈加热功率，改善冒口内部电磁场分布，增大电磁力，搅拌内部金属液，有利于热量向内传播，弥补冒口区域金属液散失的热量，因此补缩通道角增大；当电源频率为2 200～3 000 Hz时，因为电源频率过高，所以集肤层变薄，造成感生焦耳热在冒口外表面聚集过多，温度分布不均匀；并且电磁力向冒口内部渗透困难，电磁力搅拌作用减小，造成热量传递不及时[23]。因此，冒口补缩通道角增幅不明显。

4 结论

本文设计开发了冒口感应补缩技术，并利用ANSYS软件对铸锭冒口进行感应加热数值模拟计算，得到以下结论：

1) 在感应加热条件下，磁感应强度在冒口轴向上呈现“两端小，中间大”的分布趋势，在径向上磁感应强度呈幂指数规律递增，表现出集肤效应。电流强度影响磁场强度，随着电流强度的增加磁感应强度增大。磁场频率影响磁场径向分布，频率越小，磁感应强度沿径向的变化越平缓，集肤层透入深度越大。

2) 外加电磁场使得冒口熔体感生焦耳热，可有效补偿冒口热量损失，改善温度场分布，随着电流强度和电源频率的增加，冒口温度场分布越均匀，电流I=1 000 A，频率f=2 200 Hz时，冒口径向温差仅为42 K。同时，冒口补缩通道角也受外界电磁作用而得到改善，由88 °增至130 °，冒口补缩效果得到明显提升。

图10 不同电流频率下补缩通道角分布Fig.10 Distribution of the feeding channel angles at different current frequencies