三相PWM整流器不平衡电网下的功率波动抑制控制

纪伊琳，阚志忠，荣小兵

(1. 广东电网有限责任公司计量中心，广东 广州 510080；2. 燕山大学 电气工程学院，河北 秦皇岛 066004)

0 引言

近年来，由于三相PWM整流器先进的特性，如具有可实现正弦化的输入电流、单位功率因数运行、恒定的直流输出电压等特点，在各种工业中得到广泛应用，为了满足不同工作环境要求研究人员对其性能开展了多方面的研究[1-3]。然而当电网电压出现不平衡时会产生负序电流致使有功功率和无功功率波动，而功率波动又会导致网侧电流的畸变和直流侧电压的波动，若采用平衡控制算法对三相PWM整流器进行控制，不能很好抑制功率波动。为了解决不平衡电网下对三相PWM整流器实施有效的功率波动抑制控制，从而达到减小输出直流电压的波动和减小交流侧电流的畸变，Rioual等人建立了电网不平衡时三相PWM整流器数学模型[4]，推导出有功功率和无功功率的数学表达式，并选取有功功率的二倍频脉动作为控制变量来实现直流母线恒压。虽然该方法能够有效地抑制直流母线电压波动，但系统控制结构较为复杂，且电流参考中存在二倍频分量，只采用PI调节器无法实现无静差控制。为此，文献[5]提出了多重参考坐标系控制策略，该方法能够独立控制不同次谐波。针对不平衡电网电压下的控制策略研究，Suh等人提出双旋转坐标系下电流正负序变量分离控制[6-7]，该方法通过坐标变换算法将电网正、负序电流分别变换到正、反向旋转的坐标系下的直流量，并且分别利用PI调节器对直流量进行无静差控制，但是控制框架过于复杂且计算量较大，而且需要通过锁相环检测电网电压相，所以电流参考计算过程非常繁琐。另外，正负序分量提取环节存在延时，会降低系统的响应速度。上述方法都在一定程度上有所改进，但仍需要锁相环来检测电网电压相角来分离电网电压和电流的正负序分量，这不仅增加了系统的复杂度，而且如果锁相环设计不当会造成正负序分离不准确[8-9]，从而影响控制效果。

为了避免锁相环设计不当造成控制不准确和减少坐标变换，文献[10-12]分别提出了模型预测功率控制、基于虚拟磁链的直接功率控制、自适应滑模控制策略，虽然该控制策略简化了控制结构，但是模型建立复杂，控制过程仍需要大量的计算才能获得电流参考值。

综上所述，目前不平衡电网下三相PWM整流器控制策略主要存在以下三个问题：1)需要锁相环检测电网电压的相角来分离电流的正负序；2)控制系统结构复杂且电流参考计算繁琐；3)需要大容量的输出滤波电容。为此，本文提出了一种无锁相、电流参考计算简单的三相PWM整流器电网不平衡改进控制策略，首先利用电网不平衡下无功功率的新定义对三相PWM进行建模，推导出α-β坐标系下电网不平衡时有功和无功功率的数学表达式，并提出了相应的改进控制策略，使得无功功率脉动更小，输入电流畸变和直流电压波动更小，最后进行了实验验证。

1 解析模型

三相PWM整流器原理图如图1如示，图中ux(x=a,b,c)为整流器交流侧输入端电压，ix(x=a,b,c)为网侧电流，ex(x=a,b,c)为电网电压，Lx(x=a,b,c)为输入滤波电感，Rx(x=a,b,c)为输入电感的寄生电阻，idc为整流器直流侧电流，io为输出负载电流。

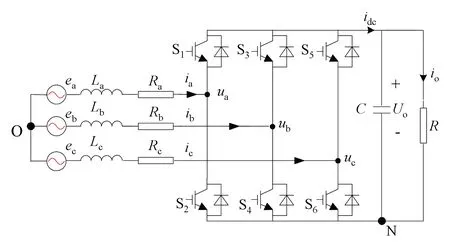
图1 三相PWM整流器原理图Fig.1 Schematic diagram of three-phase PWM rectifier

三相PWM整流器在两相静止坐标系下相应的数学模型为

(1)

(2)

由于三相系统中，任意一相的电压和电流都可以分解成正序、负序、零序分量，并且三相PWM整流器中不存在零序回路，故在不平衡电网电压条件下，电网电压和电流可以表示为[14]

(3)

(4)

在静止坐标系下(αβ)电网电压和电流可以用向量的形式表示如下：

e=eα+jeβ，

(5)

i=iα+jiβ，

(6)

结合式(5)、(6)根据瞬时功率理论可以得到输入端瞬时有功表达式为

(7)

而对于瞬时无功功率，传统的定义为

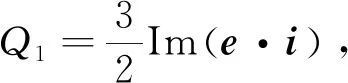
(8)

但是在电网不平衡时，传统定义下对瞬时无功功率的表达式(8)并不准确，为此文献[13]对无功功率进行了重新定义，其表达式为

(9)

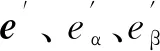
由式(3)～(9)可得

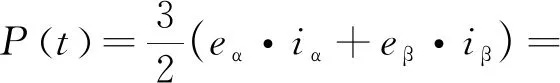
(10)

按照式(8) 传统定义下的无功功率为

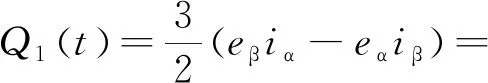
(11)

按照式(9) 新定义下的无功功率为

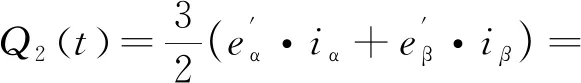
(12)

为了对比分析两种无功功率表达式的差异，现引入电网电压不平衡度，其定义为

(13)

当整流器运行在单位功率因数时网侧电流与电网电压同相位相差为零，此时有

(14)

将式(14)分别代入式(11)和(12)中，则有

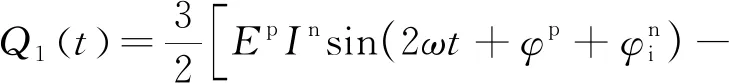
(15)

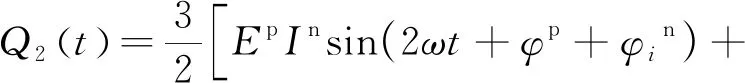
(16)

设时间t、正序电压相角φp、负序电压相角φn为固定值，并且设

(17)

将式(17)代入式(15)，则传统无功功率的表达式为

(18)

根据式(13)定义并认为电网电流正负序分量也适合该定义，则有

(19)

将式(19)代入式(18)中并以EPIP作为基准值，得到传统无功功率标幺值为

(20)

同理，把式(17)代入式(16)，则新定义的无功功率表达式简化为

(21)

得到新无功功率标幺值表达式为

(22)

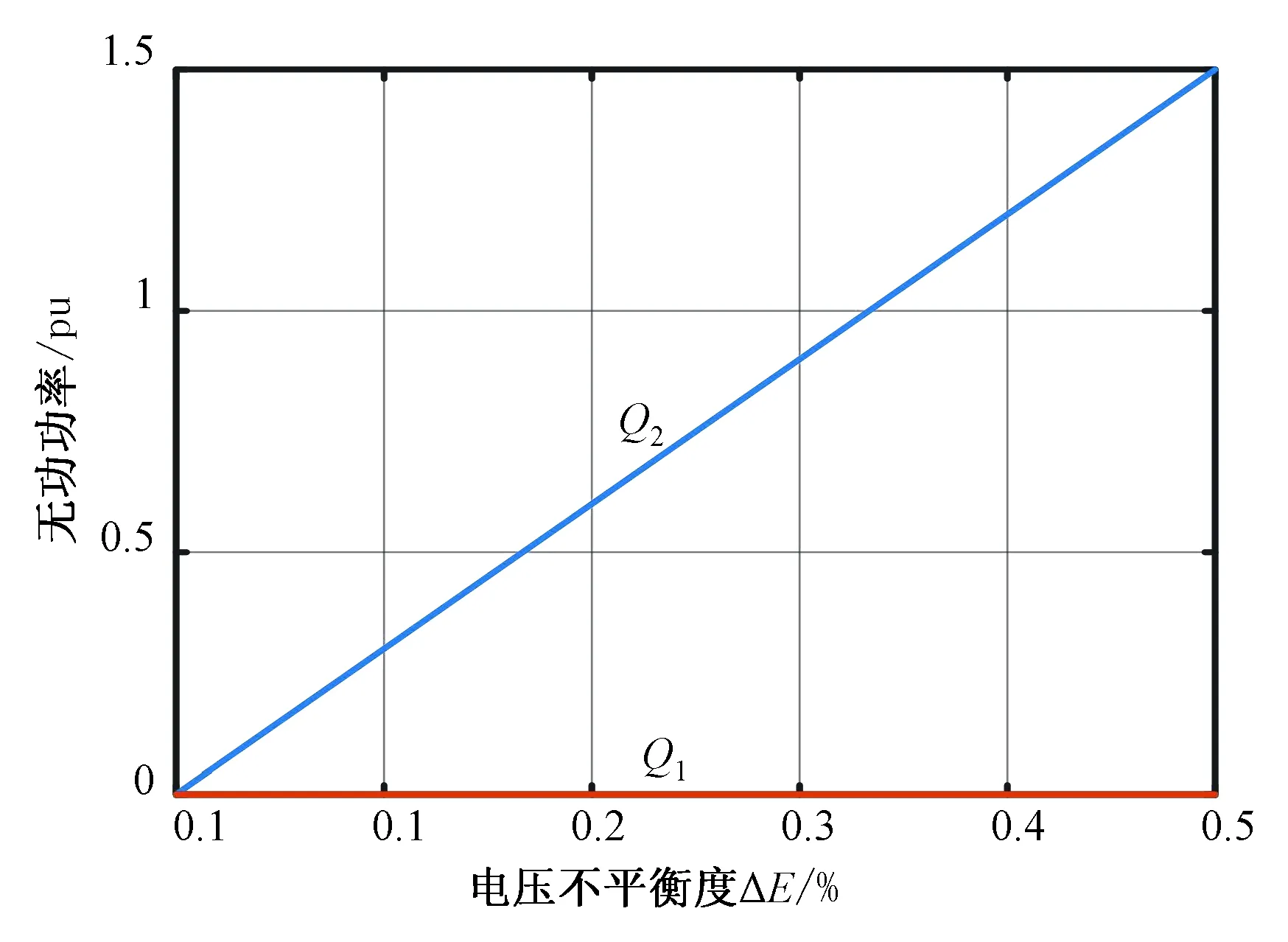
图2 ΔE、Q1、Q2之间关系图Fig.2 Relationship between ΔE、Q1、Q2

2 不平衡电网下的改进控制策略

由式(10)、(12)可知

(23)

式中，P2ω和Q2ω分别为二倍频有功和无功功率脉动。

为了实现三相PWM整流器的单位功率因数(Unit Power Factor)运行、直流母线电压恒定以及网侧电流正弦低谐波，必须满足4个约束条件，即网侧输入功率P应等于负载功率Pref(忽略变换器损耗)，无功功率Q、有功脉动P2ω、无功脉动Q2ω的参考都应设为0。这些约束条件在两相静止坐标系α-β下可以表示为矩阵的形式：

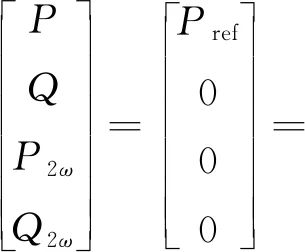
(24)

由式(24)可解得α-β静止坐标系下正负序电流的参考表达式：

(25)

根据式(25)可以得到不平衡电网下三相PWM整流器基于两相静止坐标系α-β下的系统控制框图，如图3所示。由于电流内环是在两相静止坐标系α-β下实现控制，属于交流量系统，准PR在工作点频率上有较大的增益[15]，能够实现交流量的零稳态误差，所以闭环调节器采用准PR调节器，其传递函数为

(26)

其中，kp=0.45为比例系数，kr=400为谐振系数，ωc=15为带宽和ωo为工频角频率。

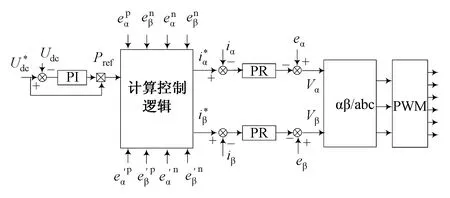
图3 系统控制框图Fig.3 System control block diagram

对图3所示的控制系统搭建了MATLAB仿真模型，电网电压不平衡度为ΔE=20%，功率与电压等级相同情况下分别对d-q坐标系下控制和本文提出的α-β坐标系下改进控制分别进行仿真，仿真参数如表1所示。

表1 不平衡电网下三相VSR系统仿真参数Tab.1 Simulation parameters of three-phase VSR system under unbalanced power grid

图4为采用d-q轴坐标系下的功率平衡算法时测得的三相PWM整流器无功功率变化仿真波形，图5为采用本文提出的不平衡改进控制算法时得到的无功功率变化仿真波形。由图4和图5可知，在电网电压不平衡时虽然这两种控制算法都不能彻底解决无功功率波动的问题，但采用本文所提出的改进控制算法时三相PWM整流器的无功功率波动明显小于采用基于双d-q坐标系下功率平衡算法的无功功率波动，这说明在抑制无功功率波动方面，本文提出的控制算法具有更好的控制效果。

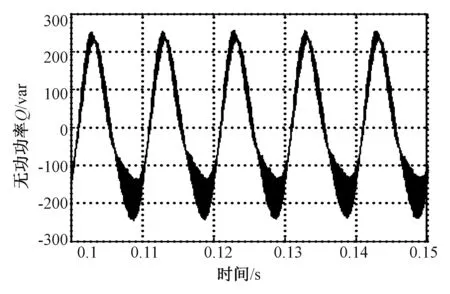
图4 基于双d-q坐标系下功率平衡控制算法的无功功率波形Fig.4 Reactive power waveform of power balance control algorithm based on dual d-q coordinate system

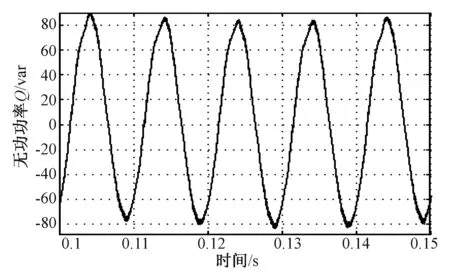
图5 改进控制算法的无功功率波形Fig.5 Reactive power waveform of improved control

3 实验验证

图6为搭建的1 kW三相PWM整流器实验平台，对所提出的控制算法和控制方案进行实验验证。主要参数如表1。

图7是采用基于传统瞬时无功功率推导的功率平衡控制算法得到的控制效果图。

利用此控制算法造成三相PWM整流器的直流侧电压波动，网侧输入电流发生畸变。由图7(a)可知，电网侧电流总畸变率约为23%，由图7(b)可知，输出直流电压存在较大的二倍频波动，其波动峰峰值约为10 V(为了清楚看出直流母线电压的波动情况，示波器设置为交流AC触发模式)。

图6 三相PWM整流器实验平台Fig.6 Three-phase PWM rectifier experimental platform

图7 基于传统瞬时无功功率的功率平衡控制算法实验Fig.7 Experiments of power balance control algorithm based on traditional instantaneous reactive power

图8为采用本文提出的改进功率平衡控制算法的实验结果。图8(a)为三相PWM整流器的输入电压和A相电流波形，其中A、B相幅值为100 V，C相幅值为50 V。可以看出，在电网电压严重不平衡下A相电网侧电流ia正弦度较好(测量表笔乘以2倍)，畸变率约为3.7%，并与A相电压保持同相位。图8(b)为三相PWM整流的直流侧输出电压，二倍频电压波动得到了很好的抑制，其波动峰峰值约为2 V。

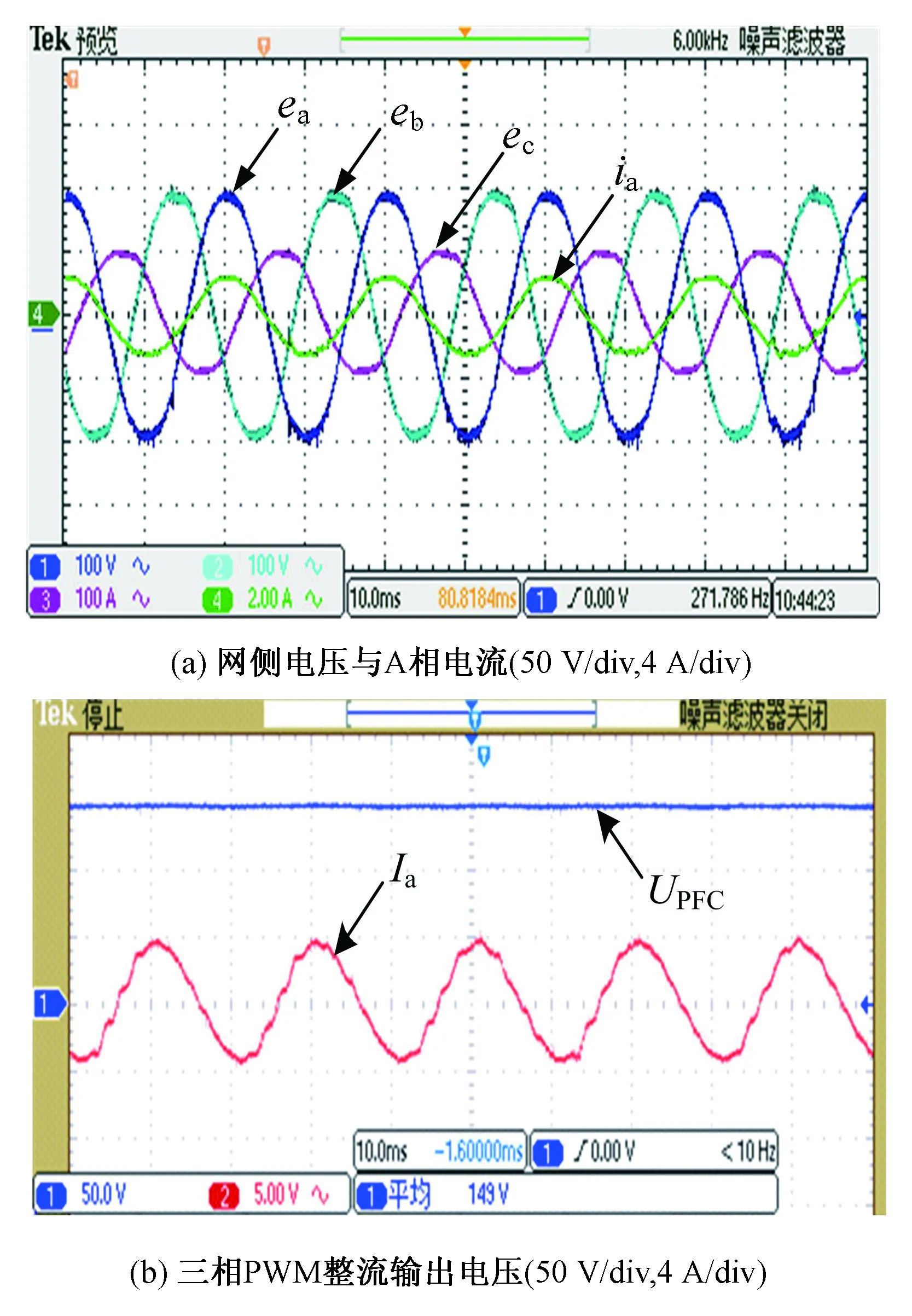
图8 改进功率平衡控制算法的实验Fig.8 Experiments of improved power balance control algorithm

由图8可知，本文提出改进控制算法在电网不平衡度大于20%的情况下，仍能保证三相PWM整流的单位功率因数运行、直流母线电压恒定以及网侧电流正弦化。

4 结论

传统对于无功功率的定义并不适用于不平衡电网，若利用传统定义进行建模，会导致所建立的模型不准确，进而影响控制效果。本文针对电网不平衡情况按照无功新定义重新推导出两相静止坐标系下PWM整流器的功率表达式，并提出了相应的控制策略。所提出控制策略与传统的功率平衡控制算法相比，使得无功功率脉动更小，输入电流畸变和直流电压波动得到明显抑制，并且能保证三相PWM整流的单位功率因数运行。