利用改进灰狼算法优化BP神经网络的入侵检测
王振东,刘尧迪,胡中栋,李大海,王俊岭
(江西理工大学 信息工程学院,江西 赣州 341000)
1 引 言
对企图入侵、正在入侵或者已经发生入侵的行为进行识别的过程称为入侵检测[1].该方法的核心技术是通过分析采集的网络数据,检测网络中的各类行为是否安全.异常检测与误用检测是入侵检测系统两种不同的检测类型.误用检测通过对已知的入侵行为和企图进行特征提取并编写进规则库,将监测到的网络行为与规则库进行模式匹配,进而判断入侵行为或者入侵企图,该方法的优点是误报率低;异常检测则是从大量正常用户行为模型中检测出攻击行为,可以对未知攻击进行检测是其显著优点.
截至目前,研究人员提出了包括基于神经网络、决策树(Decision Tree,DT)、AdaBoost、支持向量机(SVM)等多种入侵检测方法.杨彦荣等[2]将卷积神经网络和极限学习机的组合式入侵检测模型(CNN-ELM)应用于入侵检测,实验表明,该方法在NSL-KDD数据集上具有较高的检测准确率、良好的泛化能力和实时性.Ranjit Panigrahi等[3]使用J48决策树进行二元和多元分类,在ISCXIDS2012和NSL-KDD数据集上取得了较优的检测效果.Mehrnaz Mazini等[4]提出了基于人工蜂群算法(ABC)和AdaBoost的入侵检测模型,首先使用ABC进行特征选择,再使用AdaBoost进行分类,与传统方法相比,该方法的检测率得到了提高.高妮等[5]提出了基于自编码网络特征降维的轻量级入侵检测模型,该模型使用SVM对降维的数据进行入侵检测,实验证明,该模型的检测性能优于传统算法,而且能够满足网络入侵检测实时性的要求.而BP(Back Propagation)神经网络作为一种工作信号前向传播,误差反向传播的多层前馈型神经网络,在学习过程中具有很强的自学习能力、泛化能力以及强大的非线性映射能力.梁辰等[6]将BP神经网络应用于对网络攻击的入侵检测,并证明BP神经网络较传统的入侵检测具有较高的检测正确率,较低的误报率和漏报率.
虽然BP神经网络较传统入侵检测能够取得较好的效果,但BP神经网络存在初始值随机性较大以及易陷入局部最优的缺点.很多学者对此提出了相应的改进方法.刘珊珊等[7]提出了基于PCA的PSO-BP入侵检测模型,该模型通过变惯性因子粒子群算法优化BP神经网络的初始权值和阈值,取得较好的分类效果以及较优的泛化能力和实时性;丁卫红等[8]使用改进的和声搜索算法(HS)来优化BP神经网络应用于入侵检测,该办法中BP神经网络的初始值通过改进和声搜索算法来优化,提高网络检测率以及收敛速率,防止神经网络陷入局部最优;沈夏烔等[9]在入侵检测中设计了一种使用人工蜂群优化BP神经网络的方法,该方法将神经网络的误差函数作为人工蜂群算法的适应度函数,选择最优适应度函数作为神经网络的初始权值和阈值,从而缩短模型的训练时间以及避免神经网络陷入局部最优.雷宇飞等[10]将PSO-BP神经网络模型应用于入侵检测中,该模型利用粒子群算法优化得到一个最优初始值,通过修正网络误差获得最优值,实验结果证实该算法能够在较大程度上提高入侵检测系统的检测正确率.
针对BP神经网络存在的缺点,本文提出一种基于改进灰狼算法优化BP神经网络的入侵检测模型(IGWO-BP),通过改进灰狼算法获得较优的初始权值和阈值,再使用反向传播BP算法对NSL-KDD和UNSW-NB15数据集进行入侵检测.从而解决BP神经网络初始值随机较大且易陷入局部最优的缺点.
2 BP神经网络
BP神经网络可以模拟神经系统结构和生物神经网络传递信息,拥有较强的自学能力,同时能够进行自适应计算,是一种大规模非线性自适应体系.在3层BP神经网络中,假设有M个输入神经元,I个隐含层神经元,J个输出层神经元.xm为输入层第m个神经元的输入,ωmi为隐含层第m个神经元到输出层第i个神经元的连接权值,bi为隐含层第i个神经元的阈值.ωij为隐含层第i个神经元到输出层第j个神经元的连接权值,θi为输出层第i个神经元的阈值.
BP网络学习的具体过程:
1)权值和阈值通过rands随机初始化.通常,我们在[-1,1]之间随机初始化权值和阈值.
2)实验数据预处理并输入BP网络进行学习.
3)计算隐含层第i个神经元的输入,隐含层第i个神经元的输入等于输入层神经元的加权和:
再通过激活函数来计算隐含层第i个神经元的输出:
vi=f(ui)
其中,f为Sigmoid激活函数.
4)计算输出层第j个神经元的输入,输出层第j个神经元的输入等于隐含层输出的加权和:
再计算输出层第j个神经元的输出:
vj=g(uj)
其中,g为线性函数.
5)计算神经网络输出总误差:
其中,dj为神经元网络的真实输出,vj为神经网络的预测输出.
6)工作信号正向传播调整隐含层与输出层之间的权值ωij和阈值θi;误差信号反向传播调整输入层与隐含层之间的权值ωmi和阈值bi,权值和阈值修正量分别为:
Δωij=μejg′(uj)vi,Δθi=μδi
Δωmi=μδivm,Δbi=μδi
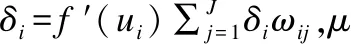
7)重复3)-6),直到全局误差小于预期误差,或学习次数到达最大学习次数.
3 改进的灰狼算法
灰狼优化算法(grey wolf optimizer,GWO)是Mirjalili等人在2014年模拟灰狼群体狩猎行为提出的一种元启发式算法[11].算法具有较强的收敛性能,实现起来简单且参数较少,因此在约束优化[12]、无人机路径规划[13]、模块组装调度[14]、PI控制器优化[15]、车间调度[16]等领域得到初步应用.然而,因为难以平衡全局和局部搜索能力以及位置向量更新时头狼位置未必最优,致使GWO算法在不停迭代过程当中极易陷入局部最优及收敛速度较慢.针对上述问题,本文对原始灰狼算法进行改进.首先,使用二维混沌映射初始化种群,可以确保数据的多样性和不重复性;接着,用非线性收敛因子取代线性收敛因子,可以很好地平衡算法的局部和全局搜索能力;最后,提出动态权重策略,使权重系数在每一次迭代中不断变化,领导层灰狼动态指导狼群前进,从而防止灰狼算法陷入局部最优.
3.1 混沌映射初始化
标准GWO算法利用随机数随机初始化灰狼群体,导致群体的多样性和不重复性难以保证,算法搜索效率在一定程度上会受到影响.因此,用混沌映射代替随机数初始化种群,可以确保种群具有较好的遍历性和不重复性,提高算法的搜索效率.文中使用二维混沌映射初始种群的数学表达式为:
(1)
其中,a,b,c为控制参数,控制参数的选择在很大程度上影响初始种群的形态.若参数a=0,混沌映射退化为线性映射,故一般要求参数a≠0且b2-4ac≠0,此时映射在不动点处具有较好的混沌性,故文中取a=-4,b=0,c=0.5,x1=0.15.
3.2 非线性收敛因子
收敛因子a对算法的全局搜索能力和局部搜索能力具有很好地平衡作用.由文献[11]可知,当|A|>1时,灰狼群体为寻找到更好的猎物将扩大搜索范围;当|A|<1时,灰狼群体为接近猎物而缩小搜索范围,此时算法应进行局部搜索.因此,该参数的选择对算法的性能有很大的影响.标准GWO算法中,收敛因子a随迭代次数增加从2线性递减到0,无法较好地平衡算法的局部和全局搜索能力.在实际应用中,更加偏向选择非线性策略调整收敛因子,以此更加准确地描述灰狼群体复杂的搜索过程.因此,本文对线性收敛因子进行改进,提出非线性收敛因子策略,以此来平衡算法的局部和全局搜索能力.数学描述如下:
(2)
其中,tmax是最大迭代次数,t是当前迭代次数.
图1为收敛因子的对比图,从图中可以看出原始收敛因子a的图像是线性递减的,在迭代过程中以相同的速率减小,算法的局部和全局搜索能力一直保持不变;改进收敛因子a的图像是非线性递减的,在迭代初期a的衰减程度缓慢,有利于进行大量全局搜索;迭代后期收敛因子a的衰减程度提高,有利于进行大量局部搜索,提高算法的搜索精度.因此,改进的收敛因子a可以更好地平衡算法的局部和全局搜索能力.
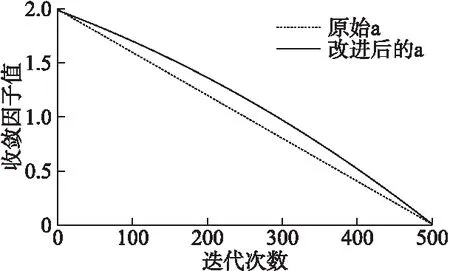
图1 收敛因子对比图Fig.1 Convergence factor contrast diagram
3.3 动态权重策略
标准GWO算法中,灰狼位置的更新公式是前3头狼位置的算术平均数,位置权重始终不变.而算法中头狼α狼不一定是全局最优解,此时随着ω狼不停地向头狼逼近,算法极易陷入局部最优.因此,本文提出动态权重策略,通过位置向量比例权重不断调节头狼所占的比重,避免算法陷入局部最优.
本文提出的比例权重公式,数学描述如下:
(3)
(4)
其中,ω狼对α狼的学习率为W1;ω狼对β狼的学习率为W2;ω狼对δ狼的学习率为W3.
灰狼位置更新公式为:
X(t+1)=W1*X1+W2*X2+W3*X3
(5)
在标准GWO算法中,位置更新公式的权重系数始终保持不变,算法极易陷入局部最优.而提出的动态权重策略,通过位置向量计算比例权重W1、W2和W3,在每一次迭代中W1、W2和W3不断变化,使领导层灰狼动态指导狼群前进,避免算法陷入局部最优.
3.4 改进灰狼算法步骤
综合以上改进策略,给出本文提出的改进灰狼算法(IGWO)步骤:
算法1.改进灰狼算法(IGWO)步骤
1.设置算法参数:种群规模N和最大迭代次数tmax.
2.用二维混沌映射产生初化始种群.
3.计算种群适应度值并对适应度值进行升序排序,适应度前3的个体位置记为Xα、Xβ和Xδ.
4.用公式(3)-公式(5)更新种群中灰狼个体的位置.判断算法是否满足迭代终止条件,若满足,则停止计算,输出最优适应度对应的位置Xα,否则,重复执行3-4.
3.5 算法的复杂度分析
假设算法最大迭代次数为tmax,种群规模为N,维数为D,标准GWO算法中,首先初始化种群,时间复杂度为o(N×D);其次计算灰狼的适应度值,时间复杂度为o(N);之后对适应度值进行升序排序,时间复杂度为o(NlogN);最后根据上述公式更新灰狼群体的位置,时间复杂度为o(N);故总的时间复杂度为o(tmax×(D×N+N+NlogN+N)).IGWO算法和GWO算法相比没有增加任何步骤,故IGWO总的时间复杂度为o(tmax×(D×N+N+NlogN+N)).对比两种算法,可知GWO算法和IGWO算法具有相同的时间复杂度,数量级为o(tmax×NlogN),但实验结果表明IGWO算法具有更高的求解精度、更快的收敛速度以及更好地稳定性.
4 IGWO-BP入侵检测模型构建
4.1 适应度函数
适应度函数使用入侵检测误差和函数,由于预测结果可由神经网络直接得到因此计算误差和非常方便;文献[17]的适应度函数为入侵检测正确率,一方面需要统计出模型正确分类个数,增加算法计算量;另一方面如果计算正确分类个数不当,会导致训练神经网络结果不理想.因此,误差和函数作为适应度函数优化BP网络可以得到较好的网络模型以及减少计算量.
IGWO通过适应度函数优化BP神经网络建立最优入侵检测模型,提高网络入侵检测正确率,降低误报率,从而提高网络整体安全性.使用网络入侵检测误差和函数作为适应度函数,数学表达式为:
(6)
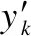
4.2 模型设计
使用IGWO算法优化BP神经网络的基本思路是求出适应度函数最好的一组灰狼位置,在迭代结束时把最好的灰狼位置作为BP神经网络的最优初始权值和阈值建立最优检测模型,基于IGWO-BP入侵检测模型框架图如图2所示,该入侵检测框架具体过程如下:
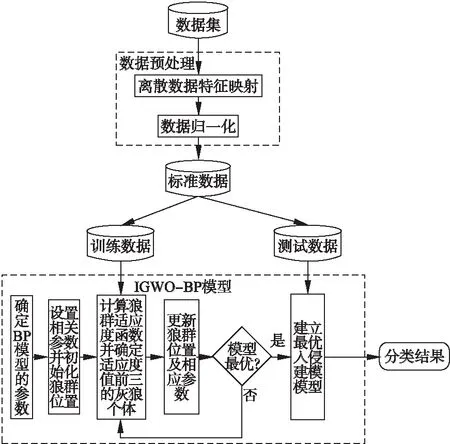
图2 IGWO-BP入侵检测总体框架图Fig.2 IGWO is used to optimize the flow chart of BP neural network
步骤1.对原始数据集预处理.预处理过程包括2个步骤:
1)离散数据特征映射.将离散型特征转化为数字型特征.
2)数据归一化.由于同种属性的数据之间差异较大,影响模型的训练效果,因此将数据归一化为[0,1]的实数.
步骤2.IGWO-BP模型训练和参数调优.
1)初始化BP网络结构:innum个输入层节点、midnum个隐藏层节点和outnum个输出层节点以及网络初始权值和阈值.
2)初始化灰狼群体:灰狼种群大小N;所求问题维度D=(innum+1)×midnum+(midnum+1)×outnum和最大收敛迭代次数tmax及灰狼种群位置xi.
3)根据训练样本和适应度函数计算灰狼适应度函数值,对适应度值升序排序并保存前3个最优狼Xα、Xβ和Xδ,更新狼群ω的位置以及非线性收敛因子a,若当前迭代次数到达最大收敛迭代次数,则迭代结束转到4);不然转到3).
4)建立最优入侵检测模型,并输入测试集进而得到入侵检测分类结果.
5 实验设置
5.1 测试函数
用4个标准测试函数[18]进行仿真实验检验IGWO算法的寻优能力.4个标准测试函数都是经典函数,包括2个单峰函数,2个多峰函数.标准测试函数的详细信息可以从表1中查看.

表1 测试函数Table 1 Test function
5.2 入侵检测数据集
1)NSL-KDD[19]:NSL-KDD是KDD CUP99数据集的简化版本,删除了KDD Cup99数据集中的冗余数据和重复记录.NSL-KDD数据集可以保证入侵检测模型不受偏见,相比于KDD CUP99数据集,它更适合于误用检测.表2给出了NSL-KDD数据集的详细信息.
2)UNSW-NB15[20]:澳大利亚网络安全中心的网络安全研究团队引入了一种称为UNSW-NB15的新数据集,以解决KDD CUP99和NSL-KDD数据集中发现的问题.此数据以混合方式生成,包含实时网络流量的正常行为和攻击行为,是一种综合性的网络攻击流量数据集.数据集用42个特征来描述,这些要素的标签为“正常”和9种不同的“攻击”类型.表3中描述了有关模拟攻击类别的信息及其详细统计信息.
我们随机选择了2000条连接记录并将其使用t-SNE[21]将NSL-KDD进行可视化如图3所示.从图3可以看出NSL-KDD数据集是非线性可分的.
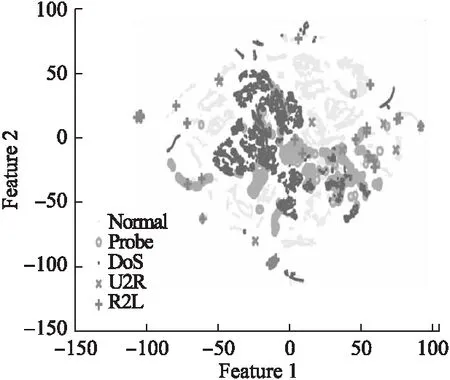
图3 NSL-KDD可视化Fig.3 NSL-KDD visualization
5.3 模型参数设置
实验是在Intel core i7双核CPU,主频2.5GHz,内存8GB,操作系统Windows 10环境下进行,实验仿真软件采用Matlab R2015b.

表2 NSL-KDD的训练集和测试集Table 2 NSL-KDD training and testing sets

表3 UNSW-NB15的训练集和测试集Table 3 UNSW-NB15 training and testing sets
群智能算法涉及参数的选择,选择较好的参数可以提高算法的收敛速度和精度.在实际应用中,群智能算法的交叉概率和变异概率一般在[0.5,1]和[0,0.5]之间取值;而在粒子群算法中,c1,c2为学习因子,也称为加速常数,分别用于控制粒子指向自身或领域最佳位置的运动,一般建议c1+c2≤4;惯性权重ω能够在很大程度上保留原始的速度.ω较大,算法具有较强的全局搜索能力,较弱的局部搜索能力;ω较小,算法具有较强的局部搜索能力,较弱的全局收敛能力,一般ω在[0.8,1.2]之间,PSO算法具有更快的收敛速度,而当ω>1.2时,算法极易陷入局部极值.
神经网络分类模型的性能受到所选参数的影响,较多的训练次数对于模型准确率的提升没有太大的影响,一般浅层神经网络训练50-150次,就可以获得较优的分类模型;而隐含层结点个数过多模型会出现过拟合现象,过少模型不能充分学习其特征,故参考文献[22]确定隐含层结点个数.
因此,文中使用的参数设置如下:在测试函数中,函数维度为30,最大迭代次数为5000次,并且实验运行30次.特别的是在GA中,交叉和遗传概率分别为0.7和0.5;在PSO中,c1=c2=ω=0.9;在DE中,交叉概率为0.99.入侵检测模型中最大迭代次数为500,神经网络训练次数为100;神经网络的输入层和输出层由实际数据集的特征和类别决定,隐含层结点个数为30.
5.4 模型评价标准
模型评价标准[23]定义如下:
准确率(Accuracy):它估计正确识别的样本数与整个测试集的比率.准确率越高,神经网络的模型就越好(Accuracy∈[0,1]).对于包含平衡类的测试数据集是一个很好的度量.准确率定义为:
(7)
精确率(Precision):它估计正确识别的正常样本与被预测为正常样本总数之比.精度越高,神经网络模型越好(Precision∈[0,1]).精确率定义如下:
(8)
F1-Score:F1-Score也叫做F1-Measure.它是精确率和召回率的调和平均数.F1-Score越高,神经网络模型越好(F1-Score∈[0,1]).F1-Score定义如下:
(9)
真正率(TPR):它也被称为召回率.它估计正确分类的正常样本与实际正常样本总数的比率.如果TPR越高,则神经网络模型越好(TPR∈[0,1]).TPR定义如下:
(10)
假正率(FPR):它估计被预测为正常样本的攻击样本数与实际攻击总数的比率.FPR越低,则神经网络模型越好(FPR∈[0,1]).FPR定义如下:
(11)
ROC(receiver operating characteristic)曲线:它的横轴为假正率(false positive rate,FPR),纵轴为真正率(true positive rate,TPR).AUC的值是ROC曲线下的面积,与ROC一起作为神经网络模型的比较指标.AUC越高,神经网络模型越好.
(12)
其中,TP(True Positive)是正确分类到正常类的样本总数,TN(True Negative)是正确分类到攻击类的样本总数,FP(False Positive)是将攻击类错误分类为正常类的样本总数,FN(False Negative)是将正常类错误分类为攻击类的样本总数.
6 实验结果分析
6.1 IGWO性能测试
表4是5种算法在测试函数上的实验结果.在单峰基准测试函数和多峰基准测试函数中,和GA、PSO、DE以及原始GWO算法相比,IGWO算法具有更好的寻优能力以及更强的稳定性.这是因为,IGWO算法使用混沌映射初始化种群、非线性收敛因子策略以及动态权重策略解决了传统GA、PSO、DE和原始GWO算法中存在的收敛精度低以及稳定性较差的问题.
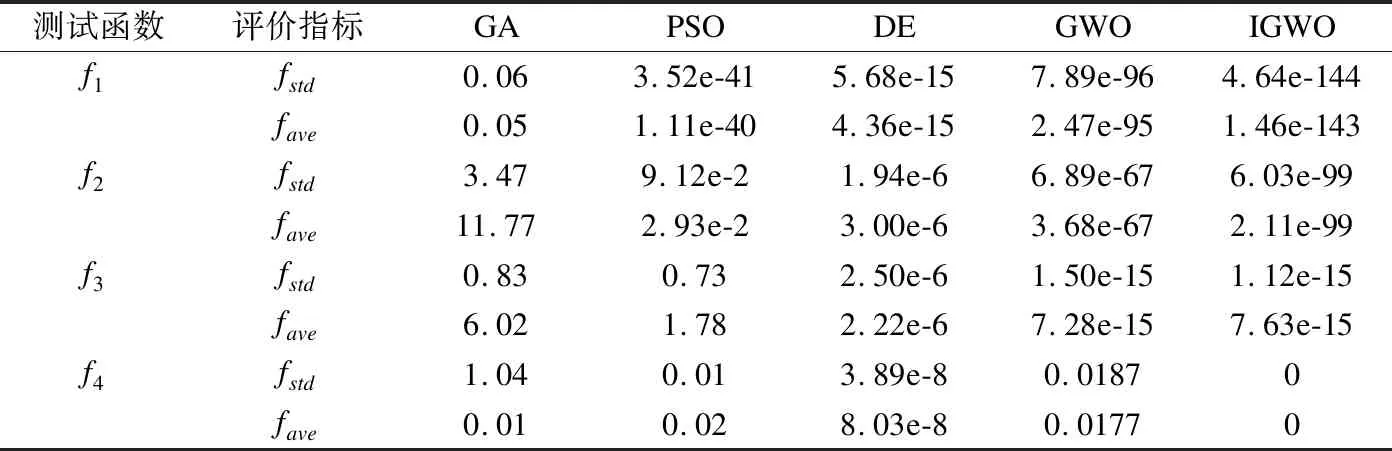
表4 单峰和多峰函数的测试结果Table 4 Result of unimodal and multimodal test function
基准测试函数二维图和函数收敛曲线图如图4所示.为方便观察,对目标函数值进行了log变换.从图4中可以看出,不论是单峰函数还是多峰函数,IGWO算法的收敛速度明显比其他算法快,收敛精度也更高.所以,IGWO算法的性能远好于其他传统算法.但其仍存在一定的缺陷,即在IGWO算法中我们采用简单的上下限的边界值对灰狼种群的越界进行替换,迭代过程中越来越多的灰狼将处于上下限的边界,导致狼群多样性减弱,在一定程度上会影响算法的收敛精度.
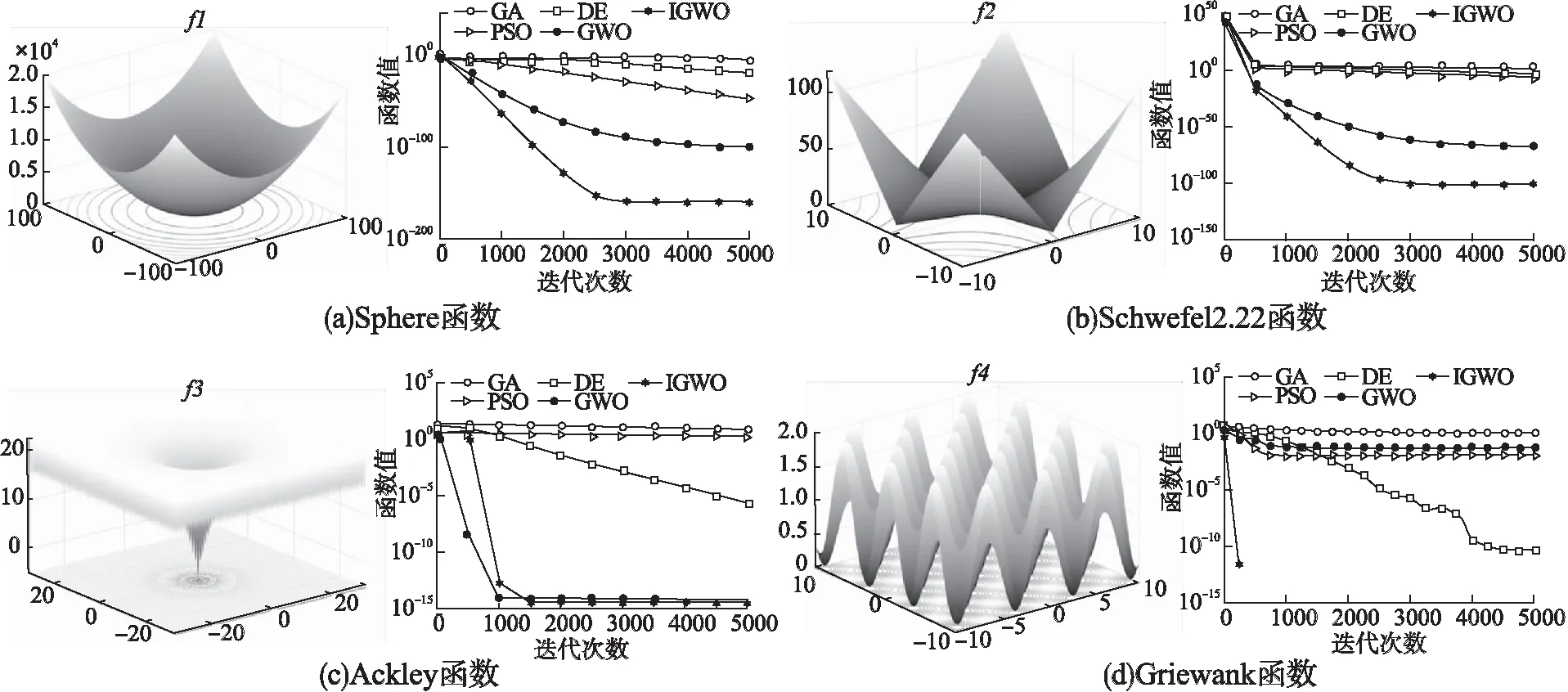
图4 基准测试函数二维图和函数收敛曲线图Fig.4 Benchmark test function and function convergence curve
6.2 IGWO-BP模型性能分析
各模型二分类的分类结果如表5所示.在准确率方面,我们注意到,IGWO-BP模型最优且AdaBoost模型的效果优于其它现有模型,分别是DT、ELM、SVM和BP.且DT、ELM、SVM和BP分类器的性能在不同的数据上性能保持不变,但AdaBoost在不同的数据集上分类器性能不同.这表明DT、ELM、SVM和BP分类器具有通用性.相比于表6和表7的多分类检测结果,各模型的二分类检测结果更优.
图5(a)和图5(b)分别是NSL-KDD和UNSW-NB15数据集二分类的准确率.图5(a)中,大部分模型的准确率位于0.8-0.95;图5(b)中,所有模型的准确率均大于0.9.相比于图7(a)和图7(b),大部分模型准确率波动幅度较小.NSL-KDD和UNSW-NB15数据集二分类准确率箱线图如图5(c)和5(d)所示.图5(c)和图5(d)中,所有模型准确率离散程度较小,且AdaBoost、DT和SVM只需训练1次分类器模型就可以保持稳定,可以减少今后模型训练次数,从而缩短模型训练时间.图图5(e)和图5(f)分别是NSL-KDD和UNSW-NB15数据集二分类的ROC曲线图.相比于其它模型,通过AUC值进行比较,IGWO-BP模型分类能力最优.且相比于多分类的图7(e)和图7(f),各模型的AUC值均更优.
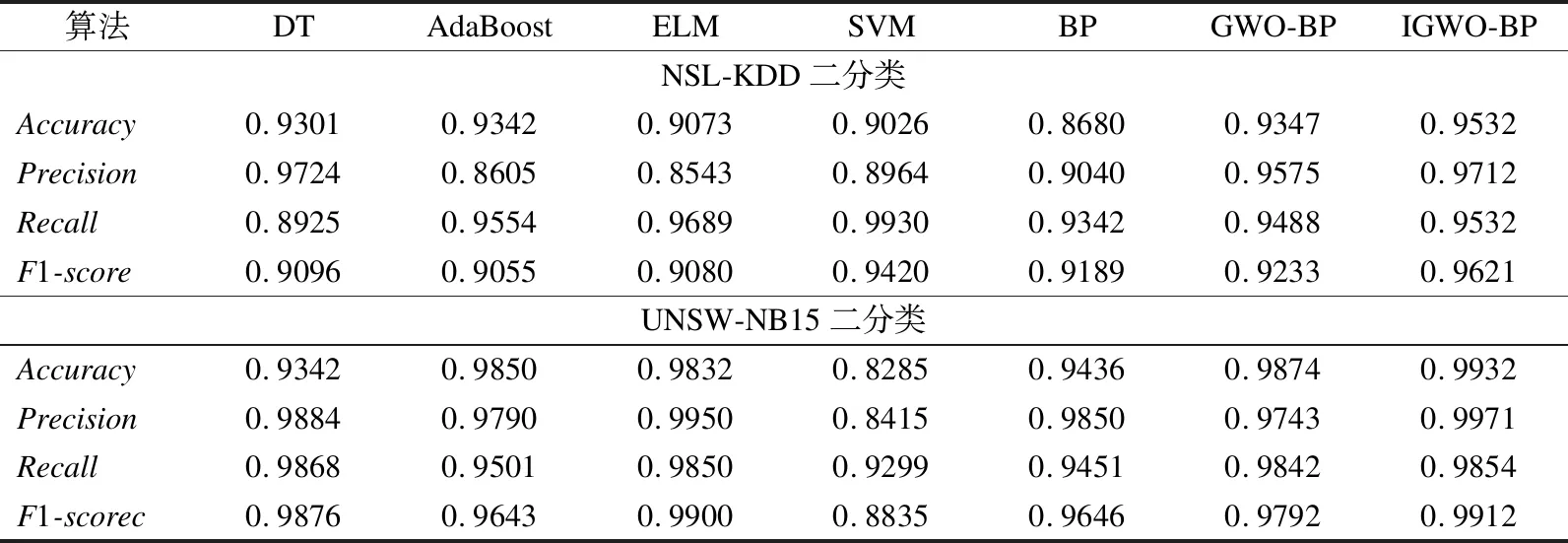
表5 二分类测试结果Table 5 Test result of binary class classification
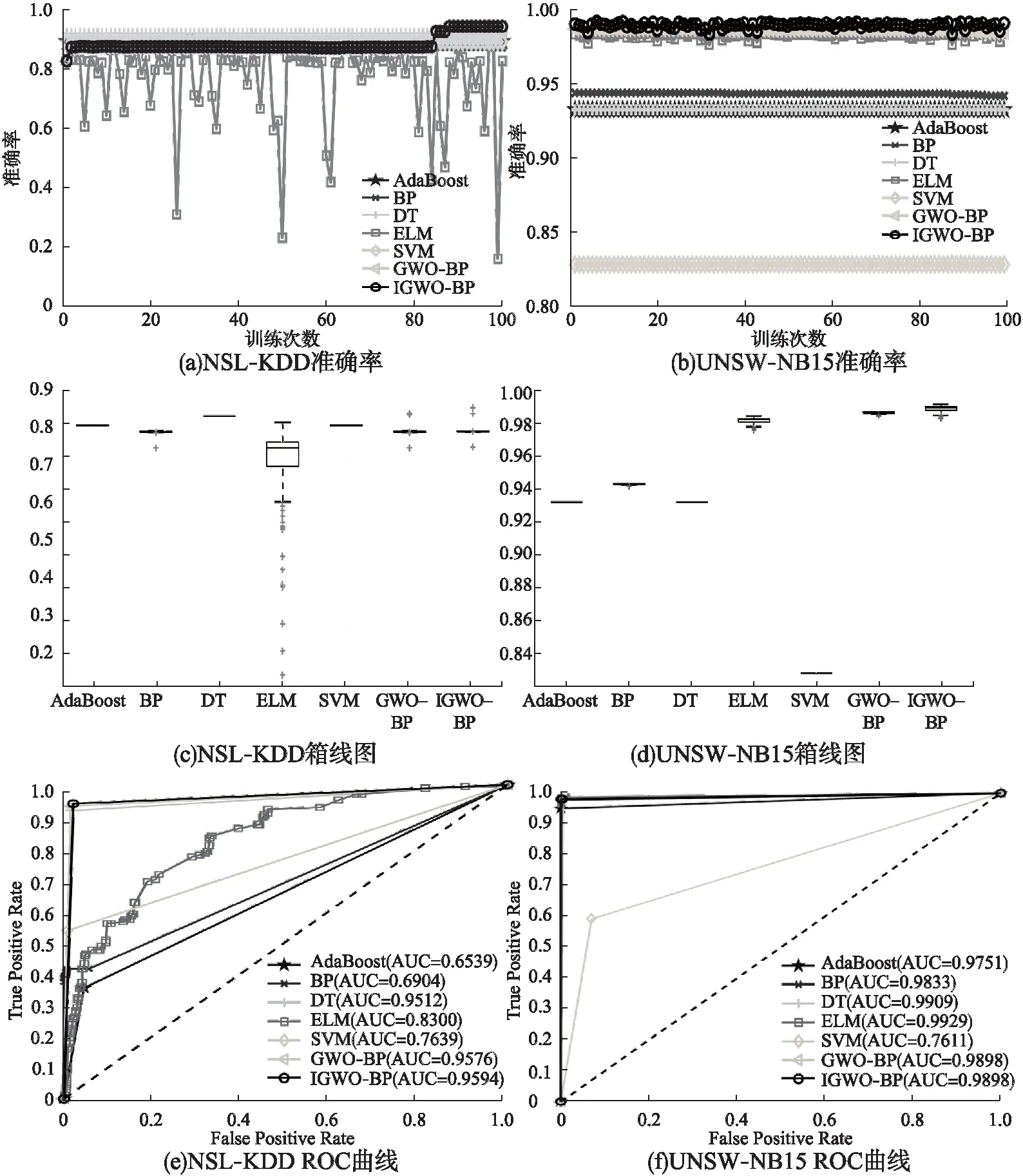
图5 二分类准确率、箱线图和ROC曲线Fig.5 Binary classification accuracy,boxplot and ROC curve
对于NSL-KDD和UNSW-NB15数据集多分类的真正率、假正率和AUC值分别在表6和表7中给出.对于NSL-KDD数据集,IGWO-BP模型的真正率、假正率和AUC值均较优,但在某些类别分类上略差于DT模型,较DT模型差0.0583.特别地,AdaBoost和SVM模型对“R2L”类别检测效果较差,真正率为0.这表明AdaBoost和SVM模型对于数量较少的特征学习效果并不是很好.对于UNSW-NB15数据集,相比于NSL-KDD数据更加复杂,故同一模型检测效果相比于NSL-KDD数据集略差.综合所有分类结果,IGWO-BP模型可以取得较优的真正率、假正率和AUC值.某些类别分类真正率略差于DT,但IGWO-BP的参数更少,计算的时间代价更少.且DT和AdaBoost的模型优于SVM和ELM模型.特别的,对于“DoS”、“Shellcode”、“Worms”类别ELM、SVM以及BP模型的分类真正率均为0.故在NSL-KDD和UNSW-NB15数据集上,IGWO-BP模型分类效果较优.
在入侵检测过程中,神经网络的每一层都有助于理解将数据分类为“正常”或“攻击”以及将攻击具体分类为攻击类别.为了更加直观的理解这一过程,我们将激活值传递到t-SNE对其进行可视化.NSL-KDD和UNSW-NB15数据集分别在图6(a)和图6(b)中表示.对于NSL-KDD,“U2R”、“DoS”的连接记录已经完全出现在另一个集群中;对于UNSW-NB15,“Worms”、“Generic”的连接记录已经出现在另一个集群中.这表明IGWO-BP已经了解了可以区分出“U2R”、“DoS”、“Worms”和“Generic”的连接记录,但还未达到最佳分区功能.对于NSL-KDD,属于“DoS”的连接记录如图6(c)所示,这些连接记录和“Normal”具有相似的特征;对于UNSW-NB15,属于“Exploit”的连接记录如图6(d)所示,这些连接记录和“Normal”、“Generic”具有相似的特征,这表明数据集需要增加更多的附加特征才能正确区分具有相似特征的数据类型.
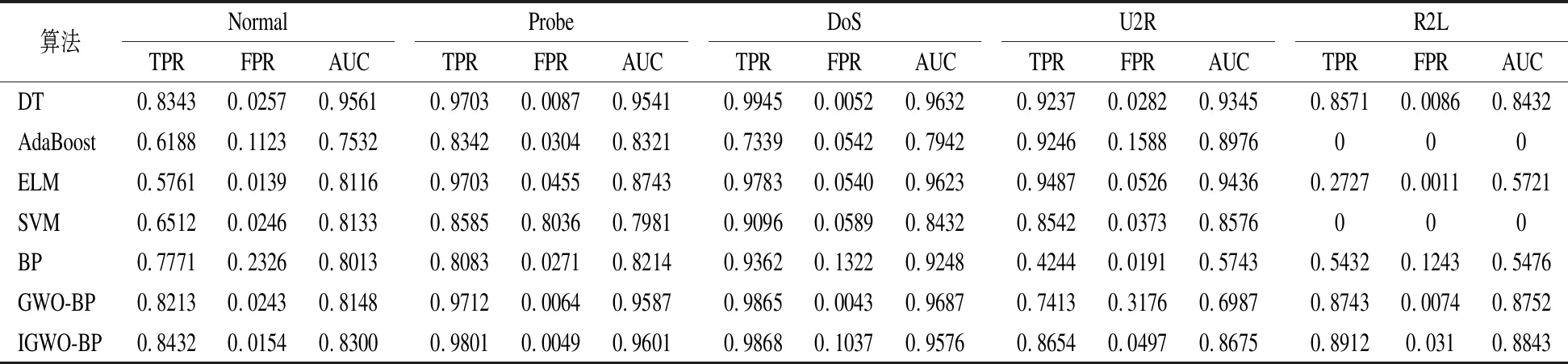
表6 NSL-KDD多分类测试结果Table 6 Result of NSL-KDD multi-class classification
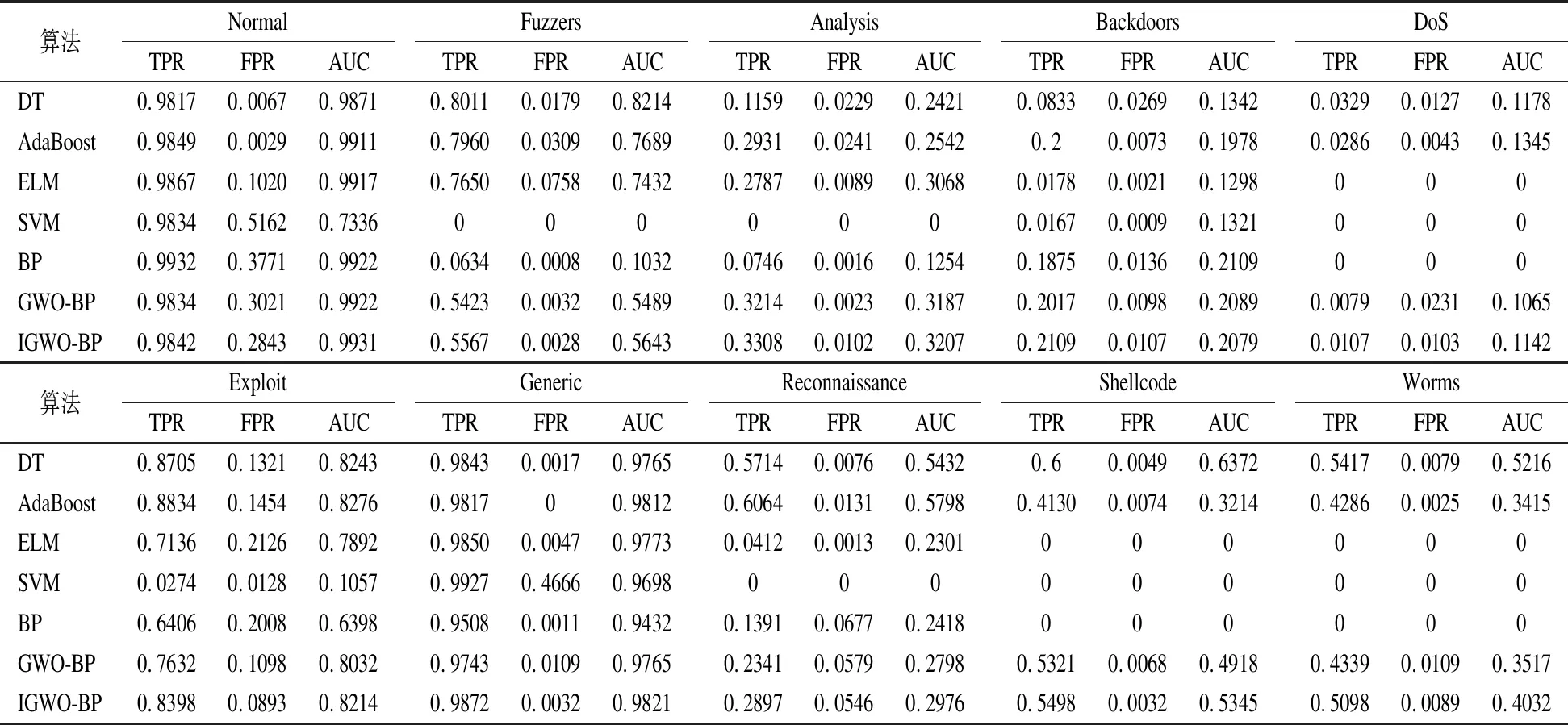
表7 UNSW-NB15多分类测试结果Table 7 Result of UNSW-NB15 multi-class classification
对NSL-KDD和UNSW-NB15数据集进行多分类的准确率如图7(a)和图7(b)所示.对于NSL-KDD数据集,算法准确率位于0.4-0.95之间;对于UNSW-NB15数据集,算法准确率在0.5-0.85之间变化.为进一步直观表示准确率,我们使用箱线图对准确率进行表示,图7(c)和图7(d)分别为NSL-KDD和UNSW-NB15数据集准确率的箱线图表示.从箱线图中可以直观看出准确率的离散程度,还可以看出AdaBoost、DT和SVM的准确率一直保持稳定,这表明AdaBoost、DT和SVM模型无需多次训练就可以得到最优分类模型,在以后实验中可以减少AdaBoost、DT和SVM模型的训练次数,从而节约训练时间.图7(e)和图7(f)分别为NSL-KDD和UNSW-NB15数据集的ROC曲线图.在大多数情况下,使用AUC作为评价指标与现有模型相比,IGWO-BP模型表现良好.这表明,IGWO-BP获得了较高的TPR和较低的FPR.
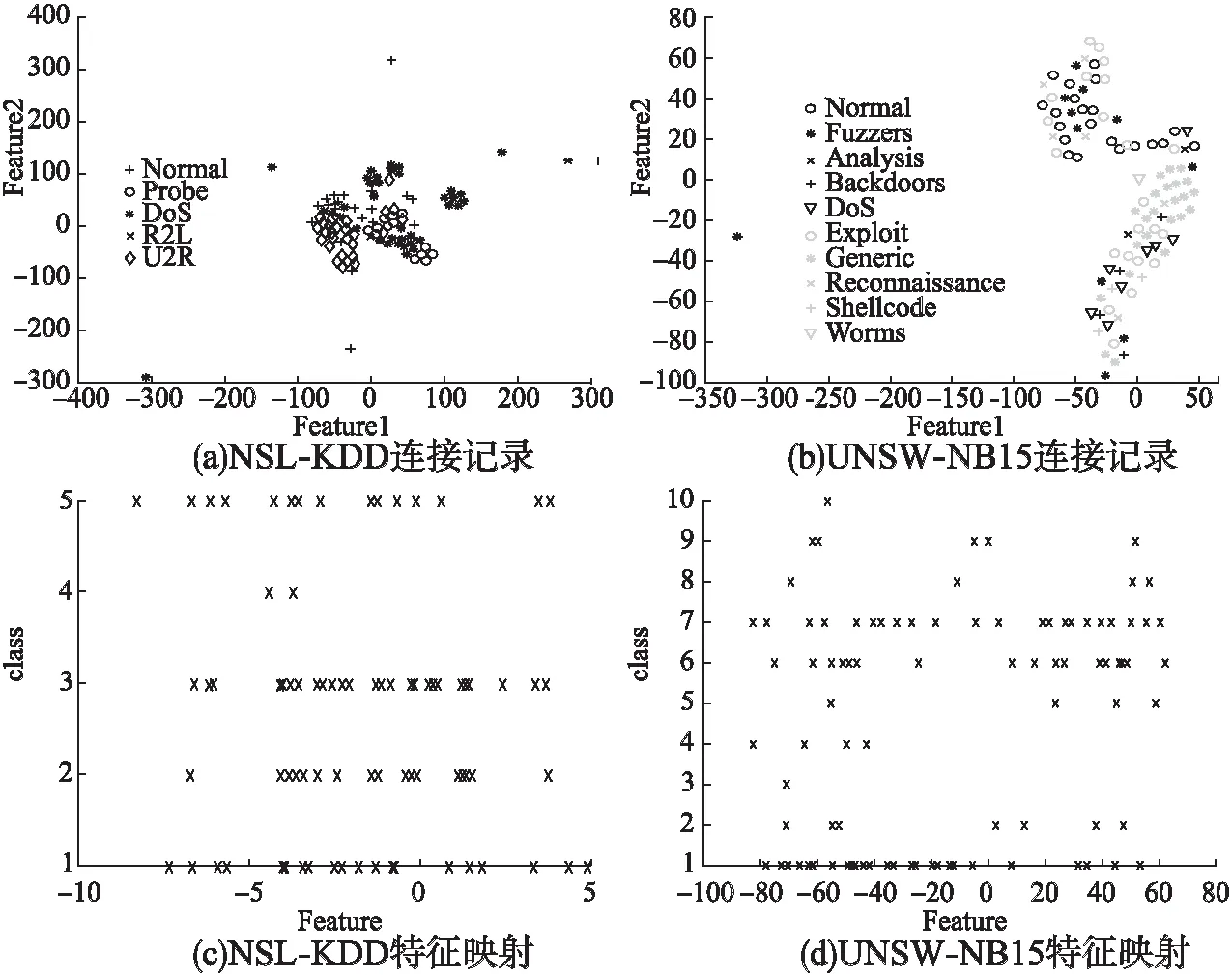
图6 最后一个隐含层激活函数的连接记录和特征映射Fig.6 Connection record and feature mapping of last hidden layer activation function
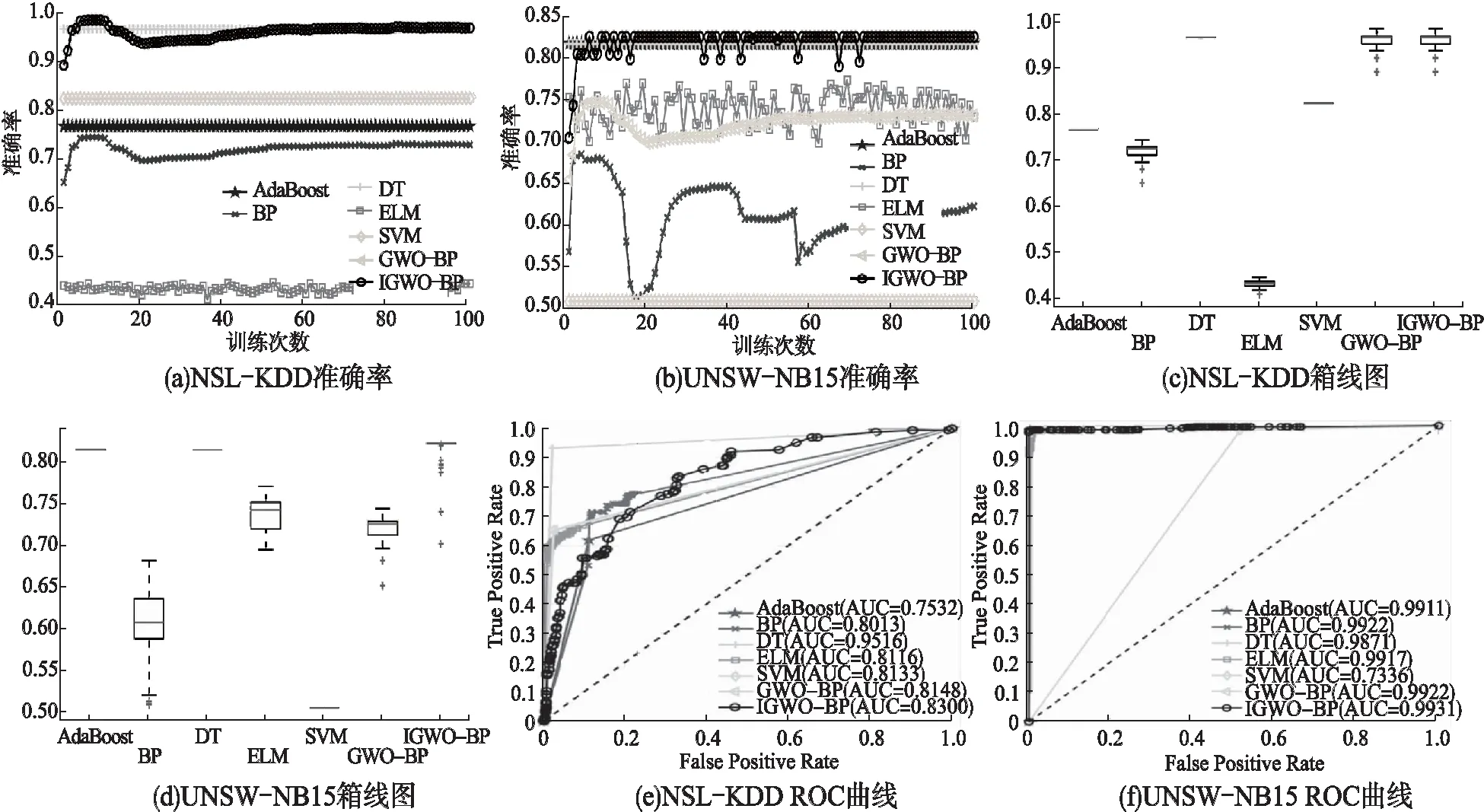
图7 多分类准确率、箱线图和ROC曲线Fig.7 Multi-class accuracy,boxplot and ROC curve
7 结 论
传统BP神经网络随机初始化权值和阈值,极易导致BP神经网络陷入局部最优.对此,本文提出一种基于IGWO-BP的入侵检测模型.首先,改进灰狼算法使用混沌映射初始化种群、非线性收敛因子以及动态权重策略优化BP神经网络的初始权值和阈值,进而应用反向传播的BP神经网络对数据集进行入侵检测.通过NSL-KDD和UNSW-NB15数据集的二分类和多分类实验结果表明,IGWO-BP模型的分类性能更优.但NSL-KDD和UNSW-NB15数据集过大,大部分模型的训练时间会过长,接下来希望通过主成成分分析(PCA)在保证入侵检测准确率的前提下,对数据集进行降维,减少入侵检测数据量,以此节约模型的训练时间.此外,由于BP神经网络一次训练时间过长,而且存在局部极小、收敛速度慢、结构选择不一以及对样本依赖性较大等缺点,所以也希望可以利用深度学习或机器学习的方法来克服BP神经网络中存在的不足.

