放疗3D剂量验证系统中光场相机点扩散函数获取

闫学文，李 华，何 良,2，乔 霈，李德源

（1.中国辐射防护研究院 核与辐射前沿技术研究中心，山西 太原 030006；2.清华大学 粒子技术与辐射成像教育部重点实验室，北京 100084）

引言

放射治疗作为癌症治疗最为常用的手段之一[1-3]，正逐渐变得越来越复杂。特别是随着调强放射治疗、弧形调控放射治疗和断层放疗等动态放射治疗技术的出现及应用，治疗方案的质量保证和质量控制也变得尤为复杂和重要[4-5]。作为质量保证和控制的关键部分，治疗前的剂量验证工作不仅能够有效地降低放疗过程中出错风险，还有助于放疗方案的精确有效制定、实施以及减少放疗副作用和降低复发率，因此具有重要的意义。

随着精准放疗[6]的飞速发展，传统剂量验证手段[7-8]在数据实时获取以及精确性方面均出现了严重的不匹配。基于此，提出了基于闪烁体的可用于动态放射治疗剂量验证的三维剂量测量技术[9]，该技术利用光场相机对受辐照后闪烁体产生的闪烁光进行三维成像，再对光亮度和剂量进行标定，从而给出三维剂量分布。

由于新型3D剂量验证系统中既充当体模又充当探测器的组织等效闪烁体是透明的，因此存在光叠加的效果。通过光场相机拍摄获得的某一个重聚焦面的亮度，是该焦平面上实际光与来自该焦平面前后其余焦平面的其他光的叠加。根据傅里叶光学理论，在线性不变光学成像系统中，像面上光亮度函数是相应物面上的实际光亮度函数和成像光学系统点扩散函数的卷积[10]。假设一个重聚焦面的实际光强度为f（i），光场相机拍摄到的该重聚焦面的光强度为g（i），则有：式中：g（i）表示第i个重聚焦面的拍摄光亮度；f（j）表示第j个重聚焦面的实际光亮度；h（j，i）表示第j个重聚焦面的光在第i个重聚焦面上叠加产生的光学系统点扩散函数。在放疗剂量验证中，我们关心的是f（j）的值，而点扩散函数h（j，i）的准确测量对f（j）的获取至关重要。本文将提出一种实验方法，对基于闪烁光场成像的新型3D剂量验证系统中光场相机的点扩散函数进行测量。

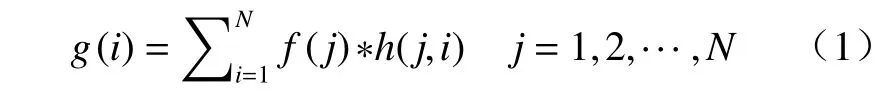
1 光场重聚焦位置标定

实验中使用的是基于微透镜阵列的Lytro Illum 光场相机[11]，与普通相机相比，光场相机最重要的特征是可以记录场景第三维信息——深度方向信息，且每一个深度平面上的光场信息均被记录在一幅原始光场图像中。利用Lytro 光场相机拍摄得到原始光场图像，再使用matlab 光场工具包[12-13]从图像处理层面进行重聚焦操作，给出每一个重聚焦层的图像。

光场重聚焦是指由光场相机捕捉场景三维光场信息，成像范围内所有深度层的光场信息均由成像探测器记录，之后通过解码该数据获取每个深度层的二维图像。这个过程主要是改变重聚焦面和成像探测器面之间的相对位置，这个相对位置用重聚焦参数α表示，任意一个α值对应一个重聚焦面。要准确获得每个重聚焦参数α对应的实际位置，必须进行重聚焦位置标定[14]，实验装置如图1所示。

图1 聚焦测距法进行重聚焦位置标定Fig.1 Calibration of refocusing position by focussing ranging method

将带有刻度的直尺斜置在图1所示光场相机视场范围内，保持斜尺刻度线水平，拍照后对原始光场图像进行重聚焦处理，得到焦点堆栈，如图2所示。图2（a）为α=0.5时的重聚焦图像，图2（b）为α=0.6时的重聚焦图像，图2（c）为α=0.7时的重聚焦图像。

图2 重聚焦获得焦点堆栈图像Fig.2 Focus stack images obtained by refocusing

将图2（b）直尺刻度方向等间隔分为70 等份，利用EVA点锐度函数对α=0.6的重聚焦图像进行清晰度评价，找出最清晰的位置，如图3所示。图3中标注约第19 等份位置处即是最清晰位置，记录此时对应直尺刻度值（见图2红线标示），即α=0.6时的重聚焦位置为142 mm 处。同理，实验过程中还标定了α=0.5 和α=0.7的位置，见图2（a）和图2（c）。

图3 EVA点锐度函数清晰度评价Fig.3 Evaluation of sharpness by EVA point sharpness function

2 刀口法测量点扩散函数

光学系统的点扩散函数为物平面上的一个点光源在像平面上所成像的光亮度分布[15]，也叫脉冲响应函数，常用高斯模型来表示。表达式为

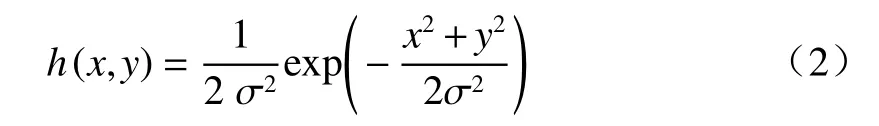
式中：σ为高斯离焦模型的参数。σ越小则像平面上光亮度分布越集中，成像质量越好。

实际情况下，理想的点光源或线光源很难获得，通常人眼对直边物体（刀口）的响应比较敏感，成像系统对直边物体响应的获取也相对容易[16]。利用相机拍摄的直边图像，计算机读取时包含直边响应图像的各行灰度数据，对每一行灰度数据采用最小二乘法进行拟合，计算拟合参数σ，带入（2）式便可得到高斯离焦点扩散函数。

本文将光学棋盘格标定板上黑白跳跃的直边区域作为输入等效阶跃函数u（x），输出e（x）由光场相机获得，然后分析输出的灰度响应。首先，使用水平仪对齐图1中倾斜直尺上142 mm 刻度位置，此时光学平台的水平面上将有一个相应的投影位置，将棋盘格标定板放在此位置并拍照，如图4所示。

图4 光场相机拍摄棋盘格标定板Fig.4 Checkerboard calibration plate shot by light field camera

对于本文假设的3个重聚焦面，结合（1）式可知每个重聚焦面的图像存在3个不同的点扩散函数，分别来自自身重聚焦面的光亮度以及另外2个重聚焦面的光亮度。综上所述，在本文示例中3个重聚焦面需要标定9个PSF。

当α=0.5，α=0.6，α=0.7时，重聚焦面分别标记为No.1，No.2，No.3。根据公式（1）可得如下关系：

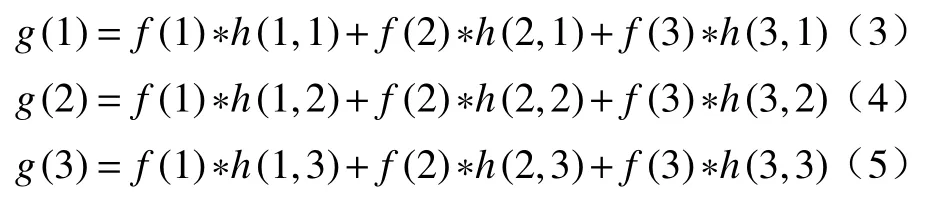
从图5所示棋盘格标定板图像中选择5个黑白跳跃区域，此时α=0.6，通过上述算法在该位置处再次重聚焦到α=0.7，即公式（5）中的h（2，3），使用最小二乘法拟合所选区域像素值的阶跃函数。

图5 棋盘格标定板上黑白跳变区域Fig.5 Black and white transition area on checkerboard calibration plate

将一个阶跃函数u（x）作为输入，在点扩散函数作用后输出为e（x）。u（x）和e（x）的函数表达式为

图5中某个红色区域黑白跳变部分的拟合曲线如图6所示。

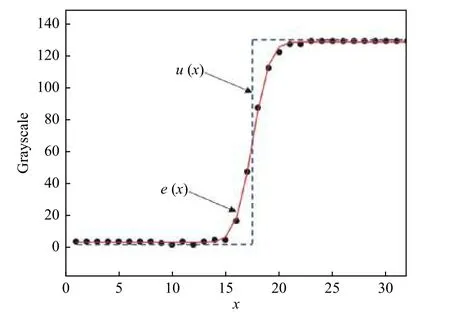
图6 灰度值的阶跃函数曲线拟合（h（2，3））Fig.6 Step function curve fitting of gray value（h（2，3））

通过拟合灰度值的阶跃函数来获得公式（7）中的参数σ，将σ代入公式（2）可获得在重聚焦位置处光场相机的高斯离焦点扩散函数。本文通过拟合图5中的5个选定区域来计算平均值σ，计算结果如表1所示。将平均值σ=1.954 9 作为公式（5）中点扩散函数h（2，3）的输入参数，给出高斯函数表现形式，如图7所示。

表1 灰度值的阶跃函数拟合得到的σ值Table1 σ values obtained by step function fitting of gray value

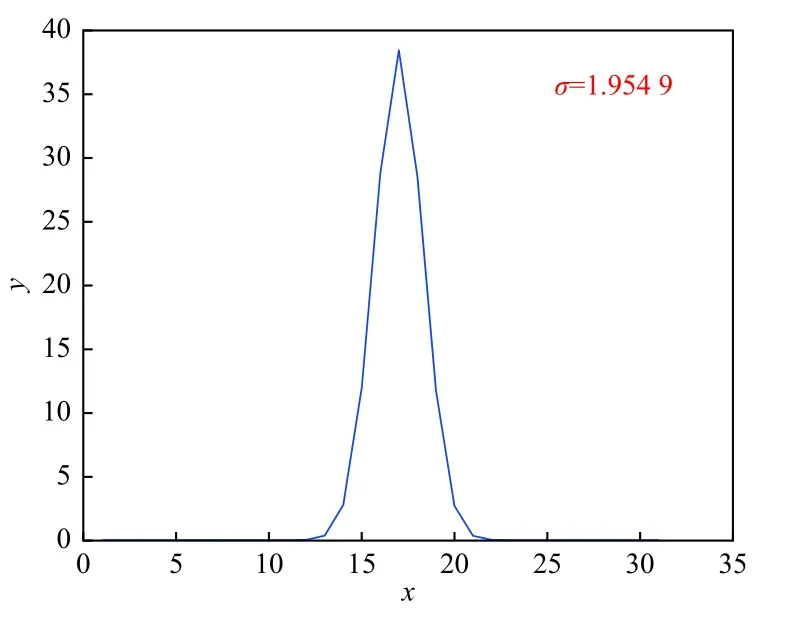
图7 高斯点扩散函数（h（2，3））Fig.7 Gaussian point spread function（h（2，3））

本文通过实验测量了3个重聚焦位置处光场相机的PSF。通过光场相机重聚焦算法获取不同焦平面上的图像g（1）～g（2）之后，只需要将表示点扩散函数的h（1，1）～h（3，3）引入（3）式～（5）式，即可以通过反卷积运算获得重聚焦面的实际图像信息f（1）～f（3）。

3 光场相机点扩散函数的规律

以上示例只考虑了3个重聚焦面的简单情况，随着光学分层的增多，需要测量的点扩散函数会以N次方的数量增加，因此有必要寻找点扩散函数的规律以减小工作量，进而提升放疗3D剂量分布测量的实时性。基于此，本文对点扩散函数进行了进一步研究，将关注的重聚焦面由3个提升至5个。根据（1）式光学分层成像原理，需要标定的点扩散函数达到25个。

首先将关注的被摄对象分为5层（i=5），重聚焦操作后进行重聚焦位置标定，将重聚焦参数α1和重聚焦位置对应起来。依次将棋盘格标定板置于5个位置处（α1，i=1、2、3、4、5）进行点扩散函数h（i，j）的参数σ 获取，结果如表2所示。表2中列表示将棋盘格标定板放置在相应重聚焦参数对应的位置处，行表示在某一重聚焦位置处对棋盘格标定板成像，然后重聚焦到5个α参数对应位置处得到的σ值。每次操作各取2个黑白跳变区域进行阶跃函数拟合，得到结果σ1和σ2，取其平均值作为最终结果。

将表2中每一行的σ值做曲线拟合，并将α2的值均做归一化处理（α1=α2时α2=0），得到的结果如图8所示。

表2 高斯离焦模型参数σ值Table2 σ values of Gaussian defocus model

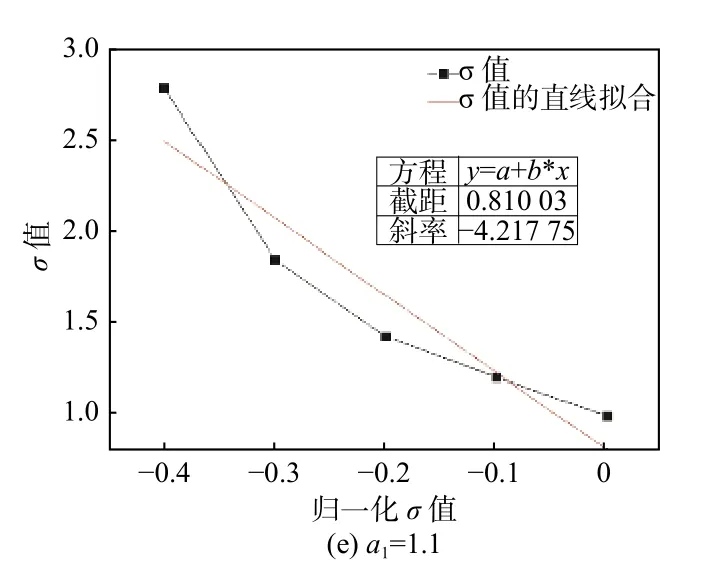
图8 σ值的曲线拟合结果Fig.8 Curve fitting results of σ values

从图8可知，对归一化α2后的σ值做曲线拟合，得到的曲线斜率绝对值在3.88～4.32之间，误差最大约为10%。由此可知，在h（i，j）的获取过程中，只要标定i=j情况下的一个σ值和另外一个σ值，便可拟合曲线得到一系列σ值，这将大大缩短三维剂量测量时间，有助于新型3D剂量测量技术的发展。

4 结论

本文通过聚焦测距法对光场相机重聚焦位置进行了实验标定，利用光学棋盘格标定板上黑白跳变的直边区域作为光场相机的等效阶跃函数输入，将CMOS 芯片记录的图像作为光场相机对阶跃函数的响应，通过刀口法实验测得了光场相机不同重聚焦位置处的点扩散函数并寻找到点扩散函数的取值规律。一方面，加深了对光场相机点扩散函数的了解，另一方面，也为基于闪烁光场成像的放疗新型3D剂量测量系统采用光学分层成像原理进行三维剂量重建打下了基础，有助于提高三维剂量测量的实时性，在放射治疗剂量验证中具有一定的现实意义。