基于有限差分法的低温防护服优化设计及仿真*

张建霞,邵创新,田 坤

(河南工学院 智能工程学院,河南 新乡 453003)

0 引言

随着科学技术的发展,人类在低温环境下进行作业的场合越来越多[1]。众所周知,人长时间处于低温环境中,热量会快速消散,进而出现一些不适,如心跳过快、呼吸不规律和动作不灵活等[2-5],严重时甚至威胁生命安全。为了能够很好地在低温环境下作业,科学家们展开了对低温防护复合材料的研究,试图做成防护服以保护在低温环境下的工作者[6-8]。低温防护服的复合材料一般具有三层结构,分别是内层织物层、中间层功能层和外层隔热层[9]。内层织物层主要提供舒适性;中间层由一种特殊的材料即相变材料构成,其可以产生并释放热量,用以延缓人体温度降低;外层隔热层主要是延缓热量对外传递。低温防护服在短时间内能有效降低低温环境对人体的伤害[10-12]。

本文针对如何有效提高低温防护服的耐低温性进行研究。首先,基于非稳态传热微分方程建立热传导模型;然后,利用函数方程插值拟合、二次搜索算法与有限差分法进行分析求解;最后,通过Matlab平台进行仿真得到低温防护服使用时间及最优厚度参数。

1 不同条件下问题的阐述与分析

本文数据主要来源于2020年华数杯高校大学生数学建模竞赛主办方[13]。为了更方便地对相关参数进行求解并高效地解决问题,提出以下假设:(1)不考虑其他不均匀热源和传热过程;(2)不考虑接触面之间的接触热阻,认为接触面连续;(3)不考虑作业服水汽、汗液蒸发等对传热传质过程的影响;(4)不同厚度的服装表面积相同;(5)消耗的衣料面积是人体表面积的1.25倍。

在以上假设的基础上,具体约束分析如下:

条件(1):无风,-40℃。已给定各层材料厚度及环境温度,通过测试得到三层材料的厚度、比热、导热系数和密度等信息。求解温度随时间分布,需要综合考虑各种传热方式及边界条件,建立完整的传热模型。通过传热模型建立时间与实测温度的分布关系,仿真得到一维热传导热量分布图,进而分析出下降到某一温度的具体时间。低温防护服传热模型考虑的是非稳态传热,即需要建立温度与时间的关系,得到整个传热过程的具体时间描述,得到非稳态过程的温度分布及传热特性。

条件(2):无风,-40℃,最大承重100kg。考虑研发制作成本、作业服笨重程度和人体舒适程度等因素建立优化目标。同样考虑最大承受重量、资金增加不超过原支出的50%和厚度范围作为约束条件,建立多目标优化模型。以站立时间最长为优化目标,以在特定低温环境下隔热达到一定效果为制约条件,求取非线性优化函数的最优解,得出最佳的厚度设计方案。

条件(3):无风,-40℃,最大承重100kg,增加在低温环境下的站立时间。改变中间层的放热能力,且各个层的温度放热能力同时放大同一倍数,使得实验者在低温环境下坚持的时间长于条件(2)中坚持的时间。由于条件(1)下的模型已经建立,可设放热能力为之前的n倍,先通过大步长遍历得到一个范围,再通过小步长遍历得到精确放大倍数,使得坚持时间大于条件(2)的时间。

2 基于非稳态传热微分方程的模型建立

本文建立的热传导模型分为低温防护服不同材料的热传导和防护服IV层到实验者皮肤的热传导模型两种。由于各材料之间的距离大概在0.3—0.7mm之间,需要考虑的传热方式为热传导和热对流[14-16]。

对于条件(1)的情况,考虑环境温度通过低温防护服到实验者皮肤的整个热传导需要,对数据进行处理,得出温度与放热能力拟合关系,然后建立低温防护服不同材料的热传导和防护服IV层到实验者皮肤的热传导模型。

明确环境温度即为I层左侧开始传导温度,IV层右侧即为实验者皮肤温度,通过数据可得到中间层温度为20.622℃,开始逐渐放热。对数据进行五阶拟合,具体关系如图1所示。

图1 温度与放热能力拟合关系图

建立低温防护服和人体的三维模型,其具有以下特征:(1)边界条件均匀分布,热传递可看做只在一个方向进行,即垂直于皮肤表面;(2)无其他不均匀热源及传热过程,研究三维传热意义不大。综合以上特征,建立一维非稳态传热模型,如图2所示。

图2 一维传导模型示意图

图中,hs代表对流换热系数,x代表空间坐标。一维传热模型不考虑上、下方向的热传导,温度变化只随坐标x发生变化。

对流换热系数hs的值如表1所示。

表1 对流换热系数表

通过边界条件值的确定以及傅里叶传热定律推导[17-20],建立一维热传导正问题模型如公式(1)所示:

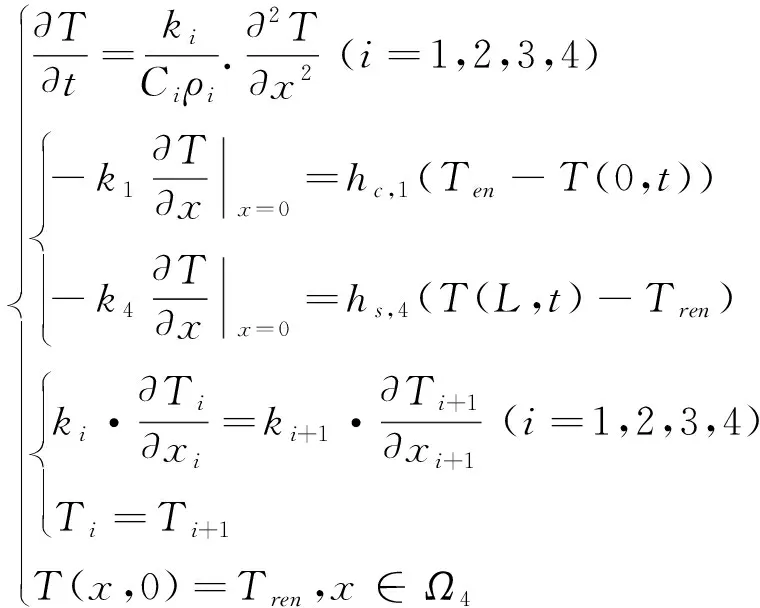
(1)

式中,q代表热流密度,i代表不同的接触面,k代表传热系数,hc,1和hs,4分别表示两端的对流传热系数,Ten表示环境温度,Tren表示人体温度。

对于条件(2)的情况,最优低温防护服的厚度设计应该使实验者在低温环境中站立时间尽可能地长,建立站立时间与防护服厚度L的多元目标规划模型,然后进行分析求解。通过数据及假设条件得到相关约束,如公式(2)所示:

(2)

式中,V表示体积,Ab表示人体有效表面积,L表示防护服材料的厚度,m表示质量,ρ表示密度,y表示各层防护服的价格,Y表示防护服的总价格,h表示身高,w表示体重,S表示人体表面积。

在相关约束条件下,服装的成本和重量是设计服装的限制条件[21]。因此将适应度函数转化成在有限厚度条件内,尽可能延长服装内侧温度降到15℃的时间。在条件(1)模型建立的基础之上,建立多目标函数,如公式(3)所示:

[obj]maxT(x,t)

(3)

对于条件(3)的情况,在成本限制条件下,增加在低温环境下的活动时间,即在条件(2)的基础上进一步优化,提高中间层的放热能力。通过Matlab绘图可得出k倍中间层放热能力优化的拟合关系,如图3所示。

图3 k倍中间层放热能力拟合图

在各种约束条件的限制下,在条件(2)模型建立的基础之上,建立多目标函数,如公式(4)所示:

(4)

3 仿真实验

对于条件(1)而言,求解热传导反问题其实是正问题和优化问题的结合[22]。根据一定的更新方式进行正问题迭代,直到满足条件为止,求得最优解。因此正问题的准确计算是能够反推反问题中待确定值的前提,正问题的求解流程如图4所示。

图4 正问题模型求解流程图

由于热量交换的边界条件比较复杂,热传导的偏微分方程也是多阶的,因此无法用一般的解析法求解,故选用有限差分法求解一维热传导方程[23-24]。为了方便计算,采用连续变量离散化的思想,将hc,1的取值离散化,设计基于连续变量离散化的二次搜索算法。具体算法流程如图5所示。

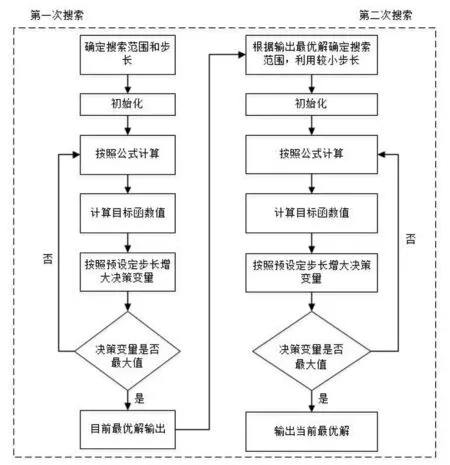
图5 二次搜索算法程序流程图

利用Matlab平台进行优化求解,如图6所示。

从图6可以直观看出温度随着时间变化的分布,在t1=17.79min时服装内侧温度降到15℃,为了安全起见,需要返回到较高温度环境中。

对于条件(2)而言,热扩散系数αi(i=1,2,3)通过Matlab计算得到,进而可得出各层放热能力的大小,如表2所示。

(a) 条件(1)约束下的三维图 (b) 条件(1)约束下的平面图图6 条件(1)约束下的热量分布优化图

表2 各层热扩散系数表

在满足相同传热性能且制作成本降低1.5倍的条件下进行厚度方案设计。因为中间层的价格与面积有关,而增加中间层的厚度几乎不影响表面积,却可以增加低温防护服的御寒能力,所以设计中间层最大厚度为0.45mm。在资金允许的范围之内,可通过Matlab仿真得出最外层和内层增加的厚度。最优设计方案如表3所示。热量分布优化如图7所示。

表3 最优厚度设计方案表

(a) 条件(2)约束下的三维图

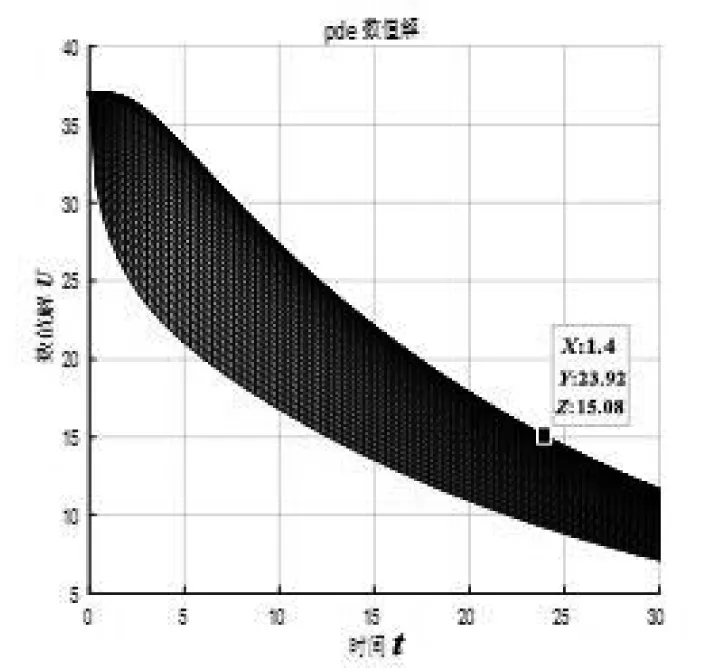
(b) 条件(2)约束下的平面图图7 条件(2)约束下的热量分布优化图

从图7可以明显看出,经过优化设计后,在t2=23.92min时服装内侧温度降到15℃,与之前相比在低温环境站立时间延长了6min。

对于条件(3)而言,在不追加资金情况下,要达到相同的低温环境站立时间,可以通过提高复合材料中间层的放热能力来实现。利用二分法,基于Matlab进行优化求解,代码如下所示。

%% 二分法

function result=dichotomy(fun,x1,x2,eps)

if nargin ～=4

errordlg

elseif fun(x1) * fun(x2)>=0

Errordlg

else

is-eps=(x2-x1)/2;

x=(x2+x1)/2;

while is-eps>=eps

if fun(x)==0

Fprintf

break

elseif fun(x1)*fun(x) < 0

x2=x;

elseif fun(x2)*fun(x) < 0

x1=x;

end

is-eps=(x2-x1)/2;

x=(x2+x1)/2;

end

if is-eps < eps

Fprintf

end

end

通过计算可以得到k=3,即在外部无风、人体静止时,不改变各层厚度的条件下,需要中间层放热能力为之前的三倍才能坚持23.92min。

通过仿真结果可以看出,中间层放热能力为条件(1)的3倍时才能使其御寒能力与条件(2)相同。条件(2)的优化只需要增加一半的成本,带来的效益却十分显著,投资与效益呈正比。条件(3)的优化所需成本比较高。

4 结论

(1)综合考虑各种传热方式和边界条件,建立了热传导模型,并应用于低温防护服设计的优化,为满足不同条件下的实际需求对问题进行优化求解。结果显示,建立的数学模型符合实际,具有比较强的通用性和推广性。

(2)通过Matlab软件进行优化求解,简单方便,容易实现。

(3)模型复杂因素较多,不能对其进行全面的考虑,如由于可行解数量较少,故采用了遍历搜索,而遍历搜索只适用于可行解数量不大的情况,否则运行时间会过长。

本文研究的总体思路、数学模型建立与优化求解简单而且易懂,可以为低温防护服的设计提供参数参考与理论依据。