无人机巡航路径规划在多船舶跟踪中的应用研究*

牟光臣,修素朴,闫雷兵

(河南工学院 电子信息工程学院,河南 新乡 453003)

0 引言

随着无人机技术的快速发展,无人机在各个领域得到了广泛的应用。无人机具有成本低、灵活性好、风险小、效率高等特点,将其用于海事监管,如海事巡航、调查取证和应急响应、搜救救援、船舶油污泄漏监测和检查等,可有效扩大监管范围,减少违法违规现象,助力海事系统现代化建设,提升海事科学水平发展[1],而在海事监管中对船舶的跟踪是需要解决的关键问题之一。

国内外研究无人机在海事监管中的应用成果较多,如固定翼无人机利用航空摄影来实现边境巡逻,海上污染跟踪以及海洋和环境研究,并具有自动着陆和起飞功能[2]。在基于单个或多个无人机平台利用视觉图像构建真实的3D地理信息,来预测地质灾害的发生[3]。无人机在海事巡航和溢油检测方面的应用,以及无人机巡航基地选址与建设[4]。Royset等[5]使用TSP(Traveling Salesman Problem)模型来规划无人机任务,目的是找到爆炸装置(Improvised Explosive Devices,IED)和放置简易爆炸装置的恐怖分子。该任务规划使用预处理程序、整数线性程序、IED预测模型与TSP模型相结合的方法规划出最优的无人机路径。Mufalli等[6]提出了定向运动问题为无人机进行传感器选择和路径规划建模。无人机飞行之前可以携带不同传感器,传感器的选择取决于采集目标信息的要求和目标的类型。这样,特定目标值与目标和每种传感器的组合相关联。然而实际上,无人机(Unmanned Aerial Vehicle,UAV)规划问题的输入参数可能是不确定的,由于无人机在不确定的动态环境中运行,因此有效的无人机任务规划应该能够应对环境变化和期望变化。Adolf等[7]提出了一种基于概率路线图与蚁群优化算法相结合的任务规划方法,该方法在无人机低空飞行时具有较好的规划效果。

本文基于无人机机载摄像机,依据相机成像原理,对一定水域内的船舶进行跟踪,并结合无人机自身性能的约束和船舶的位置、航向和航速,利用聚类优化算法对无人机巡航路径进行规划。

1 问题描述

如何飞行才能够对多船舶进行最长时间的跟踪,这就涉及无人机的巡航路径规划问题。解决怎么飞行的问题,需要从以下三个方面着手:

(1)无人机巡航高度。根据相机成像原理,无人机飞行高度越高,则机载相机的视场范围就越大,相机的分辨率就越低。

(2)无人机巡航速度。无人机巡航速度越低,对船舶的跟踪时间就越长,但对于整个巡航任务来说就需要更长时间来完成任务。反之,巡航速度越快,执行同样的巡航任务所花费的巡航时间就越短。

(3)无人机航向。无人机飞行方向确定了相机视场对船舶的覆盖方向。

如图1所示,假设某一自由航行区域内有多条匀速直线运动的船舶S1,S2…,Sn,且船舶的当前位置(x1,y1),(x2,y2),…,(xn,yn)、速度v1,v2,…,vn和航向θ1,θ2,…,θn为已知量,虚线矩形框为无人机在不同高度时的视场范围。在此基础上,规划无人机的巡航路径来对该区域内对多条船舶进行跟踪,使得跟踪船舶的数量和时长达到最优。

图1 区域内船舶分布图

2 算法设计

2.1 无人机性能约束

无人机自身性能约束是根据无人机的模型参数来对其运动过程中的特定动作进行约束,了解无人机的模型参数能够更好地规划飞行路径,避免规划出无人机无法完成的动作或超出无人机自身性能的飞行路径。在任务规划中,飞行高度、速度和航程通常需要作为无人机自身性能约束而被考虑[8]。

(1)飞行高度。在无人机海事巡航中针对不同的飞行任务对无人机飞行高度也有限制,通过最大和最小飞行高度的限制可以保障无人机的飞行安全。

依据机载相机成像的基本原理:(l,w)=f(h,θ),其中l×w表示机载摄像机的有效视场范围,h为无人机飞行高度,θ为机载相机视场角。

假设跟踪船舶需要连续测量n帧图像，且无人机运动速度为Vu，船舶速度为Vv，船长为L，L+n(Vu+Vv)=f(hmin,θ)，则hmin为无人机对船舶跟踪的最低飞行高度。

最大飞行高度hmax需要结合无人机性能、地理环境、飞行天气情况及相机的分辨率来设定。则无人机每一段飞行航迹的高度hi( 1, 2, 3,…,n)需满足如下约束：

hmin≤hi≤hmax

(1)

在不同飞行高度下,无人机对长江中不同类型船舶的航迹信息采集如图2所示。图2中(a)、(b)分别给出了无人机在66.5m和500m的飞行高度下对航行中船舶的航迹信息采集结果,可以看出无人机飞行高度在66.5m时航迹清晰,无人机飞行高度在500m时航迹较为模糊,但航拍范围较广,由此可见无人机的飞行高度是影响航迹信息采集的因素之一。同时由于无人机螺旋桨旋转会形成气流旋涡使水面上空气流絮乱,在距离水面较低飞行时有坠机风险。通过多次试验验证无人机巡航高度为[50,500]m时,航迹信息采集效果较为理想。

(a)飞行高度66.5m,船长126.4m

(b)飞行高度500m,船长126.4m图2 无人机不同飞行高度航迹信息采集图

(2)最大航程。由于受到无人机电池电量的约束，无人机在执行巡航任务中，需要考虑航程问题，设定无人机飞行极限距离的80%为无人机的最大航程。为了保证巡航任务的顺利执行和无人机的安全，其飞行的总距离需要小于最大航程，否则会对无人机的安全性造成严重影响。假设Lmax为无人机最大航程，且某条飞行轨迹上有n个飞行目标点，i( 1,2,3,…,n-1) 为第i段的飞行距离，则无人机在沿着该轨迹飞行完成任务时，无人机总航程L的约束为：

(2)

(3)最大飞行速度。在对船舶进行检测跟踪的过程中,需要综合考虑无人机检测效率和跟踪时间的问题。为了提高检测效率,需要较大的飞行速度对检测区域进行巡航检测,而对检测到的船舶跟踪时就需要合适的飞行速度来对船舶进行长时间的跟踪,故需要对无人机的飞行速度进行约束,图3为无人机对单船舶跟踪示意图。

图3 无人机对单船舶跟踪示意图

假设无人机在飞行高度一定且满足无人机对船舶跟踪最小距离的条件下,无人机对船舶跟踪的最大飞行速度为:

Vu=((dmin-kL)/t-Vv)/cosθ

(3)

式中，Vu是无人机速度，dmin是船舶中心到视场边沿的最小距离，dmin=min(dx,dy)，L是船舶长度，k是船舶回旋圈船长系数，t是跟踪船舶的最小时间，Vv是船舶速度，θ是无人机与船舶航向夹角。

2.2 优化模型建立

无人机飞行高度与所拍摄目标的距离越远,所拍目标的成像分辨率越低;反之,无人机飞行高度与所拍摄目标的距离越近,所拍目标的成像分辨率越高。成像分辨率与摄像头的性能参数有关,摄像头参数、航拍高度、地面分辨率三者的关系如下[9]:

H=f·GSD/e

(4)

式中,H表示无人机巡航时的飞行高度,单位 m;e表示相机镜头像元尺寸,单位 mm;f表示相机镜头焦距,单位 mm;GSD表示地面分辨率,单位 m。

无人机巡航高度与相机视场成正比关系,即高度越大视场范围越大,能够覆盖到的船舶就越多。由公式(4)可知高度与相机分辨率成反比,为了能够更好地对船舶进行跟踪,需要采集到船舶更清晰的图像信息,故需要根据船舶的长度和相机分辨率来确定巡航高度。

假设无人机在最大飞行高度Hmax下，机载相机视场能够覆盖m条船舶，在m条船舶中最小船舶的长度为Lmin，则无人机巡航高度可表示为：

H=f{e,k,GSD,Lmin}

(5)

假设无人机飞行高度一定，在某个时刻，视场范围内有n条船舶，那么该区域内的船舶在时刻t下的轨迹点可表示为：

s={t,xi,yi,vi,θi,li,ri|i∈n}

(6)

式中，(xi,yi)表示船舶的经度和纬度，vi表示航速，θi表示航向，li表示船长，ri表示船舶邻域半径。

无人机在时刻t下的轨迹点可表示为：

u={t,xu,yu,vu,θu}

(7)

式中，xu,yu表示无人机的经度和纬度，vu表示无人机速度，θu表示无人机航向。

在视场范围内的最大时长跟踪函数：

max(t)=f{t,xu,yu,vu,θu,xi,yi,ri}

(8)

根据2.1节中无人机性能的约束条件，可以得出无人机路径规划约束条件为：

(9)

2.3 优化算法设计

优化算法设计的目的是实现对巡航区域内最多船舶的跟踪，并且要求对船舶跟踪时间最长。通过机载AIS获取无人机附近n条船舶的信息，假设船舶位置分别为(x1,y1),(x2,y2),…,(xn,yn)，其航向分别为θ1,θ2,…,θn，其速度分别为v1,v2,…,vn。假设无人机在最大飞行高度Hmax下，机载相机的视场为l和w，相机最小分辨率为GSDmin。以m=n,n-1,…,3条船舶位置形成多边形，如果该多边形的最大外置矩阵的长度lb和宽度wb，以及最小船舶的分辨率GSD满足如下公式：

(10)

则无人机的位置坐标(xu,yu) 可表示为：

(11)

因此，可得到无人机在飞行高度H下最多能对m条船舶进行跟踪。

在巡航高度一定情况下，为了使无人机对m条船舶进行最长时间的跟踪，需要对无人机的飞行速度vu和vθ进行优化。

利用余弦相似度聚类方法对区域内的m条船舶进行航速航向的聚类，和向量最大的值即为无人机飞行的航速和航向。

余弦相似度是利用空间中的两个向量夹角的余弦值来度量向量的差异性。余弦值越趋于1表示其夹角越近似0度，即表示两个空间向量越相似，通过计算两个向量夹角的余弦值可衡量向量之间的相似度[10]。余弦相似度推导公式如下：

(12)

旋转矩阵：

(13)

(14)

式中，(φx，φy)为相机视场角。

无人机跟踪约束条件：

(15)

3 仿真实验结果与分析

机载相机在跟踪船舶时需要考虑相机的视场范围,由于相机的视场角是固定不变的,故相机视场范围与无人机飞行高度成正比关系,如图4所示,length和width曲线分别表示视场的长度和宽度。

图4 高度与视场范围的关系图

在高度一定情况下,为了能对船舶进行最长时间的跟踪,需要对无人机的航向和航速进行优化。图5为自由航行区船舶航行示意图,图中有12条船舶,其航行位置、航向和速度由图中向量表示,o表示船舶当前位置,箭头方向表示航向,箭头大小表示航速。

假设无人机飞行高度h=350m,则视场范围l=3000m,w=2250m,为了达到对区域内所有船舶最大时间持续跟踪的目的,需要对无人机的航速和航向进行优化。可根据公式(11)计算出无人机的位置Pu=(-300,-25)m，无人机的航向用余弦相似度来求解，和向量最大的方向即为无人机航向。图6为航速、航向的和向量示意图，以原点(0,0)为坐标中心，最大向量方向角θ=189.7°。对全部船舶的速度向量进行求和得到无人机的速度Vu=2.83m/s。图7中向量up表示无人机的运动向量。

根据无人机对船舶跟踪的约束条件，用MATLAB对其进行仿真，仿真结果表示最大连续跟踪时间为34s。图8和图9分别为在无人机坐标系中和大地坐标中，无人机跟踪过程中船舶的运动状态。

根据无人机对船舶跟踪的约束条件,用MATLAB对其进行仿真,仿真结果表示最大连续跟踪时间为34s。图8和图9分别为在无人机坐标系中和大地坐标中,无人机跟踪过程中船舶的运动状态。

图5 自由航区船舶航行示意图

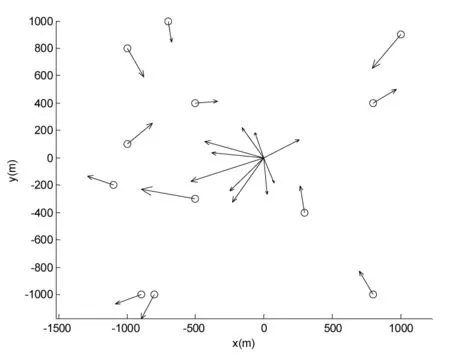
图6 船舶航向和航速的和向量示意图

图7 无人机位置、航向和航速图

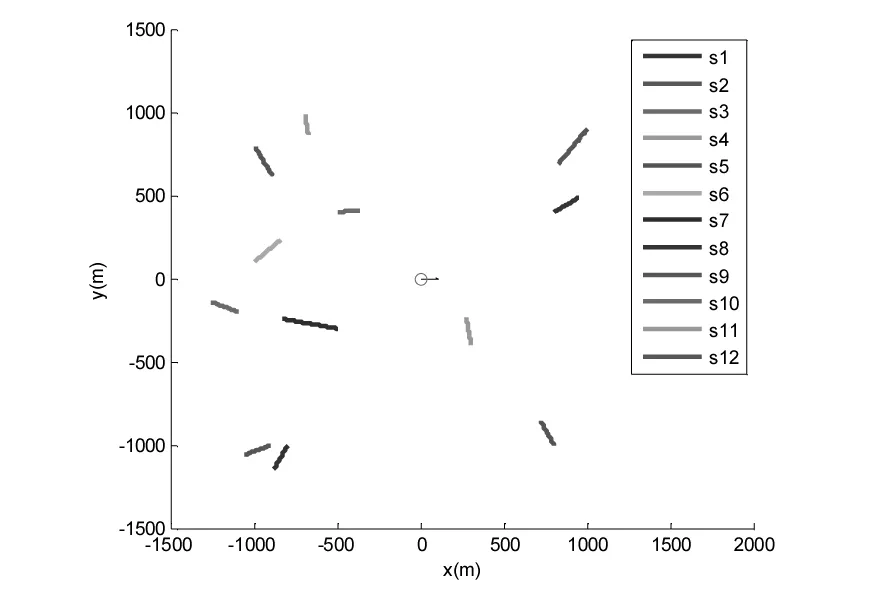
图8 无人机跟踪过程中船舶运动的仿真示意图(无人机坐标系下)

图9 无人机跟踪过程中船舶运动仿真示意图

4 结论

本文提出的基于船舶最大时长跟踪的无人机路径规划算法,在无人机飞行高度一定,即视场范围确定的情况下,采用加权平均的方法得到无人机的位置,利用余弦相似度聚类方法对无人机航向和航速进行优化来完成对多船舶最长时间的跟踪。仿真实验表明,该规划算法可以对区域内的多条船舶进行时长最优的跟踪。