不同填土高度下箱涵内力变化规律的研究

刘 凯

(山西路恒交通勘察设计咨询有限公司，山西 太原 030006)

1 研究背景

箱涵是指由一个或者多个矩形钢筋混凝土箱节组成的涵洞。当道路排水防洪或者跨越相交道路时，往往会采用箱涵，箱涵具有整体性好，结构稳定，对地基承载力要求低等优点，因此被广泛应用于公路、铁路建设，对道路建设起着至关重要的作用。以往箱涵设计过程中采用的平面杆系模型，将箱涵简化为二维模型来进行计算，将填土模拟为土柱，且忽略土柱之间的相互作用，因此平面杆系计算模型具有一定的局限性，得出的结论不具有代表性。

本文采用平面杆系模型对不同填土高度的箱涵进行结构计算，同时依托Abaqus对不同填土高度的箱涵进行有限元分析计算，对比两次计算的结果，以期能够对箱涵随着填土高度变化的内力变化规律有一个更加准确的认知，为箱涵更加准确的结构计算提供强有力的理论支撑。

2 采用平面杆系模型对不同填土高度的箱涵进行结构计算

本文采用平面杆系模型[1-4]分析填土高度1 m，3 m，5 m，7 m，8 m下箱涵的内力，此处设跨径6 m的箱涵。假定路基填料摩擦角为Φ=15°，容重为γ1=19 kN/m3，混凝土容重为γ2=26 kN/m3，汽车荷载为F，汽车荷载分布面积为A，箱涵结构示意图如图1所示。

2.1 拟定截面尺寸

3号、4号板板厚度为a=0.6 m，1号板、2号板板厚度为b=0.6 m，h为填土高度；q为最不利荷载布置时恒载与活载竖向荷载的组合值(q=1.2×P+1.8×Q)，ep1,ep2是由恒载引起的水平压力,e车是由活载引起的水平压力。

2.2 荷载计算[1]

荷载计算参照[1]，具体如下：

恒载竖向压力[3]：

P=γ1h+γ2b

(1)

其中，P为恒载竖向压力，kPa；γ1为填土容重，kN/m3；h为填土高度，m；γ2为箱节容重，kN/m3;b为1号板的厚度，m。

恒载水平压力[3]：顶板处:

(2)

底板处:

(3)

其中，ep1为恒载引起的顶板处水平压力，kN;ep2为恒载引起的底板处水平压力,kN;Φ为土摩擦角。

活载竖向压力[3]：

(4)

其中，Q为活载竖向压力,kN；F为车辆荷载轴载，kN；A为车辆荷载分布面积。

活载水平压力[4]：

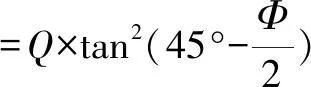
(5)

其中，e车为活载引起的水平压力。

2.3 计算过程及数据汇总

根据平面杆系内力计算方法[4]，取涵洞轴向1 m长度进行计算：

在荷载计算完成的基础上需要对箱涵进行以下的结构计算，具体的计算过程详见文献[2],本文不再赘述。

1)构件刚度计算。

2)求涵洞四个角点(A，B，C，D)的弯矩。

3)求1号、2号、3号、4号杆的轴力。

4)求1号、2号、3号、4号杆的跨中截面剪力和弯矩。

得到计算结果如下：

将计算所得的数据汇总成表，表1为主要截面弯矩汇总表，单位为kN·m。

表1 不同填土高度箱涵的弯矩计算汇总

2.4 结果分析

为了便于观察，这里将汇总结果绘制成折线图，图2表示填土高度和弯矩关系折线图，单位为kN·m。

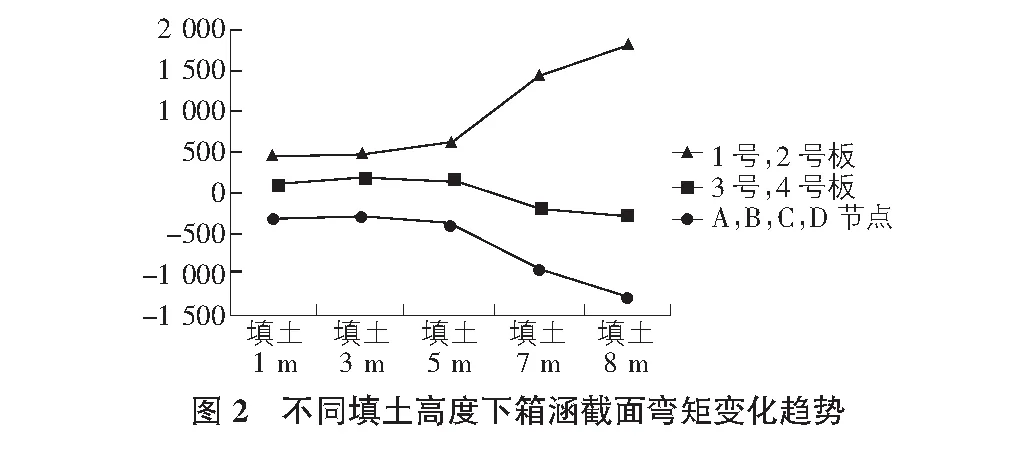
通过对计算所得的数据进行分析发现：在填土1 m～5 m范围内，箱涵的四个节点以及1号板、2号板、3号板、4号板弯矩变化幅度不大，填土高度大于5 m以后，1号、2号板弯矩有了明显幅度的上升，3号板、4号板弯矩向负方向有明显幅度的增长，四个节点弯矩向负方向也有明显幅度的增长。

这种现象是由于在填土1 m～5 m范围内，随着填土高度的增加，填土产生的竖向荷载不断增大，同时汽车荷载由于填土高度的增加而被扩散，两者此消彼长，因此箱涵受力状态没有发生明显变化；当填土高度大于5 m时，汽车荷载由于在土壤中的扩散，对箱涵的影响已经变得很小，填土高度成为箱涵所受荷载的主要影响因素，因此箱涵各控制截面的弯矩有了明显幅度的增长。

3 利用Abaqus进行有限元分析

接下来采用有限元分析方法[1-3]对同样的箱涵模型进行分析，观察箱涵在不同填土高度下的变形以及应力分布云图，并且与平面杆系模型计算出来的结果进行对比，来得出结论。

3.1 建立模型

这里对建模过程只系统介绍，不进行详细描述，具体见文献[6]。

1)采用三维模式、实体单元、拉伸的方法建立路基和箱涵模型，并赋予相应的材料参数。

2)将路基和箱涵进行装配，定义接触，接触面法向定义属性为硬接触，切向定义属性为摩擦接触。

3)建立分析步，并且对边界进行约束，按照规范施加相应的车辆荷载。

4)对模型进行网格划分。

5)建立作业，并运行分析。

按照上述方法分别建立模型，得到应力分布云图如下：

如图3a)～图3e)分别对应填土高度1 m，3 m，5 m，7 m，8 m的箱涵变形情况以及应力分布情况。

3.2 结果分析

为了便于观察，这里将建模结果绘制成折线图，图4表示填土高度—应力的关系折线图，单位为MPa。

4 结果对比

通过对箱涵变形情况以及应力分布云图的观察发现：随着填土高度的变化箱涵的受力是比较复杂的。在有了平面杆系模型计算结果的基础上，进一步分析，发现在填土1 m～5 m时，箱涵各个控制截面的应力相差不大，由此可以看出在填土1 m～5 m范围内，随着填土高度的增加，填土产生的竖向荷载不断增大，同时汽车荷载由于填土高度的增加而被扩散，箱涵的受力不发生明显变化，这个结果与采用平面杆系模型计算出来的结果相一致；在填土高度为5 m～7 m时，箱涵各个控制截面的应力发生了较大幅度的增长，可以确定汽车荷载由于在土壤中的扩散，对箱涵的影响已经变得很小，填土高度成为箱涵所受荷载的主要影响因素，这个结果与采用平面杆系模型计算出来的结果也相一致。不同的是在填土高度大于7 m时，箱涵各控制截面的应力并没有产生明显的增长，反而有小幅度的减小，这个结果与平面杆系模型计算出来的结果产生了分歧。

通过对箱涵变形和应力云图的仔细观察发现在填土高度为3 m时，箱涵已经产生了不太明显的纵向变形，填土高度为7 m时，云图上所观察到的纵向变形效果已经非常明显。同时可以看到，在不同填土高度下，箱涵的1号、2号板的应力等值线呈椭圆状扩散，3号、4号板的应力等值线也是由箱节中部向两边逐渐扩散，由此可以得出结论，箱涵的受力并不是简单的单向受力结构，而是非常复杂的空间受力结构，而采用平面杆系模型进行计算时，忽略了箱涵的纵向受力影响，这是导致箱涵在填土高度7 m～8 m的范围内，用有限元方法计算得出的结果与平面杆系模型计算得出的结果产生了分歧的原因之一；在荷载计算中，将填土荷载模拟为光滑接触的土柱并不准确，实际上土体之间的相互作用是非常复杂的，这是导致产生上述分歧的第二个原因。

5 结语

通过以上分析可以得出结论，箱涵在实际工程中的受力是非常复杂的，平面杆系计算模型将箱涵简化为二维平面杆系模型所计算出来的结果具有一定的参考价值，但误差相对较大，对箱涵的内力的变化规律无法精确的反映，而且随着填土高度的增加，误差也逐渐增大。箱涵随填土高度的变化，土体之间的相互作用越来越复杂，涵洞纵向受力对涵洞结构的影响也越来越明显，因此随着填土高度的增加，箱涵的内力变化并不是严格的线形增长。