保守确定性失效法中非线性能量吸收因子研究

郑 泽 华

(中冶建筑研究总院有限公司，北京 100088)

1 概述

核电站抗震裕度评估方法主要有三种：EPRI-SMA[1]，NRC-SMA[2]和PSA-based SMA[3]。其原理是根据成功路径或者事件树/故障树筛选出结构、系统和部件(SSC)，采用易损性方法(SFA)或保守确定性失效的方法(CDFM)进行分析，确定高置信度低概率失效值(HCLPF)。

SFA法计算中值能力、随机性和不确定性系数时需要大量的主观判断，计算过程较为复杂且具有较大的不确定性[4]。CDFM法相比SFA法，其计算过程更程序化且确定，由抗震能力和抗震需求两部分组成。抗震能力包括材料强度、非线性能量吸收因子等; 抗震需求包括荷载组合、地震响应谱和阻尼等[5]。其中，非线性能量吸收因子Fμ是考虑延性对结构耗能能力的影响的一个参数。但是，各类文献中鲜有对Fμ的计算方法进行报道，多数取值1.25[4,6]。但是，对于不同的结构，其耗能能力必定受到其材料本构、构件的截面尺寸以及结构布置等情况的影响，故而Fμ的取值也会受到影响。因此，有必要给出一种方法来确定Fμ的取值。

本文旨在研究非线性能量吸收因子Fμ与结构性能间的联系，并通过多模态Pushover分析方法尝试给出其计算方法。然后以多层框架结构为例，以时程分析结果作为基准，验证该方法的准确性。

2 结构性能的描述

结构的抗震性能水准，是指结构在遭遇某一地震作用下预期的最大破坏程度。《建筑抗震设计规范》中“小震不坏、中震可修和大震不倒”的“三水准”的抗震设防思想，实际上就是一种关于结构抗震性能的描述。但是“三水准”设防只是性能化设计的雏形，并没有量化。抗震性能水准应该根据结构的抗震设防类别、设防烈度、结构类型、使用功能、投资大小、震后损坏和修复难易程度等条件综合分析和论证后确定[7]。

另一方面，结构的性能水准是一个宏观概念，与结构的破坏程度相关，而结构的破坏程度又需要由结构的反应参数来表示。既可以采用单一的参数作为各性能水准的目标参数，例如：力(如基底剪力、层间剪力)、位移(如顶点位移、层间位移)、应力、应变、速度、加速度以及能量等[8]；也可以参考多个参数以确定更全面的性能水准。

根据目前的研究进展，采用变形量作为抗震性能设计参数，是一种能够实现基于性能的抗震设计思想同时亦能兼顾计算效率的方法。众多学者对其进行较为深入的研究。其中黄悠越等[8]通过建立构件性能指标与结构性能指标的关系，得出结构基于性能的层间位移角性能指标。各性能水准下框架结构的层间位移角性能限值指标为：完好0.004、轻微损坏0.005、轻～中等破坏0.009、中等破坏0.012、不严重破坏0.016。

3 非线性能量吸收因子Fμ的计算

3.1 单自由度体系的Fμ的计算

几乎所有的结构和部件在失效前都会表现出一定的延性[6]。结构遭遇较大地震作用时，延性是结构耗能并减小地震作用的破坏，保证结构安全性的一个重要因素。非线性能量吸收因子Fμ就是考虑延性对结构影响的一个参数。可从单自由度体系的弹性最大位移和弹塑性最大位移的计算中推导出非线性能量吸收因子Fμ的计算公式[9]。

对于一个单自由度体系，在地震波的作用下达到弹性极限位移。根据反应谱理论，其位移为：

(1)

而将地震波扩大Fμ倍后作用到该单自由度体系上，该体系将由弹性状态进入到弹塑性状态。可近似计算结构的弹塑性最大位移：

(2)

而根据延性的定义：

(3)

且有：

(4)

根据此四式可以推出：

(5)

其中，m为质量；Sa为反应谱加速度；Ke为弹性刚度；fe为弹性刚度Ke对应的频率；βeq为等效阻尼；δe为弹性位移；Fμ为非线性能量吸收因子；Keq为等效刚度；feq为等效刚度Keq对应的频率；βeq为等效阻尼；δi为塑性位移；μ为延性。

3.2 等效刚度Keq和等效阻尼βeq的计算

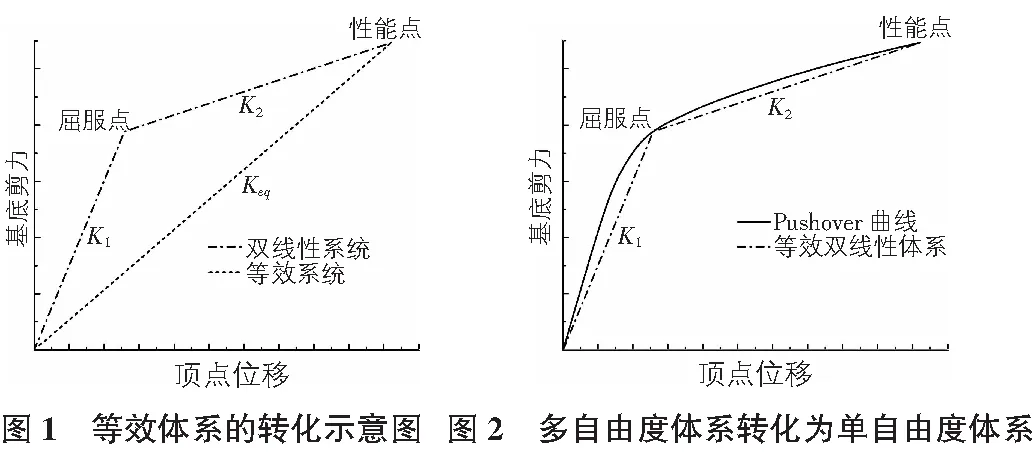
若该单自由度系统的本构关系采用弹塑性双线性本构关系，如图1所示，假设屈服后的刚度K2与初始刚度K1的比值为系数α，即:

(6)

结构的等效刚度:

(7)

而延性的定义：

(8)

再由图中的几何关系可以求出：

(9)

结构的等效周期则为：

(10)

根据文献[10]给出的等效粘滞阻尼公式:

(11)

(12)

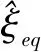
3.3 多自由度体系的Fμ的计算

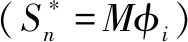
简化后的体系有两个关键点：屈服点和性能点，如图 2所示。其取值根据文献建议的最大层间位移角来确定。屈服点表示结构在该点达到结构的完好状态界限；性能点表示结构在该处达到结构的各阶性能状态。取屈服点和原点之间的割线刚度为结构的初始刚度K1，取屈服点和性能点之间的割线刚度为屈服后刚度K2。

为了考虑高阶振型对结构响应的影响，本文用Fμ=∑FμiMi(Mi为第i阶振型质量参与系数) 组合来得到整个结构的Fμ，通常情况下所取的模态数应满足质量参与系数大于90%。

4 数值算例分析

4.1 算例说明

为了验证改进的多模态Pushover分析法计算非线性能量吸收因子Fμ的正确性和有效性，本文将同时采用弹塑性时程分析法对8层混凝土框架结构进行分析，并把结果进行比较，来探讨这两种方法所得结果的差异。此结构柱距6 m，层高4 m，梁截面尺寸为400 mm×650 mm，柱截面尺寸为650 mm×650 mm，混凝土强度取C30。

4.2 自振特性

首先对结构进行模态分析，结构的前6阶模态的参数如表1所示。从表1中可以看出，结构的第一阶和第四阶模态即为X向振动的第一阶和第二阶模态，其X向振型示意图如图3,图4所示。两者X向质量参与系数合计已超过90%，可以选择这两者作为控制振型。

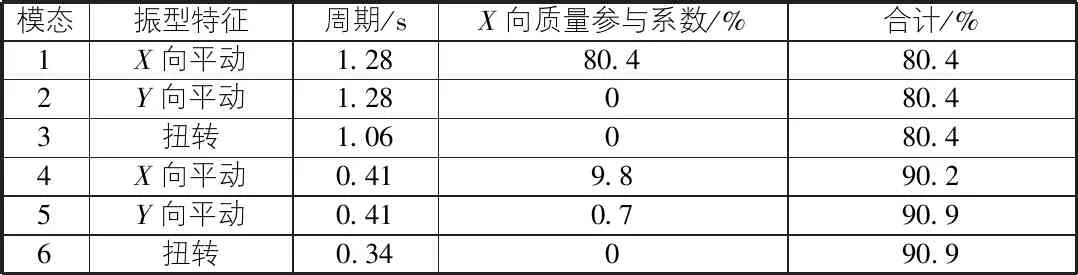
表1 结构自振特性

4.3 Pushover分析与Fμ计算

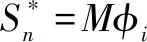
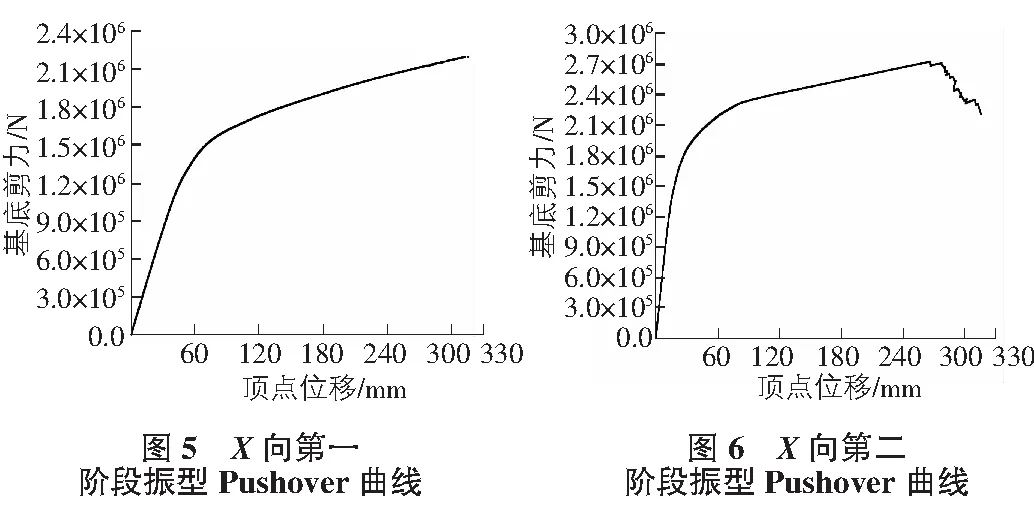
4.4 结果分析

选取五条地震波对结构进行非线性时程分析，以验证上述方法的准确性。先将地震波调幅至使结构达到弹性极限状态，再将地震波分别放大Fμ倍，使结构依次达到各阶性能极限；进而对比两种方法的差异性。

从表2中可以看出：采用多模态推覆分析法计算非线性能量吸收因子Fμ的结果，接近非线性动力时程分析的结果，其误差范围均控制在7%以内。而采用单一模态推覆分析法，其误差可达到20%。这是因为在结构进入弹塑性阶段时，结构刚度的衰减导致其基本周期增大，高阶振型起的作用越来越明显，其影响已不可忽略；而模态推覆分析法一定程度上考虑了高阶振型的影响，从而减小了计算误差。

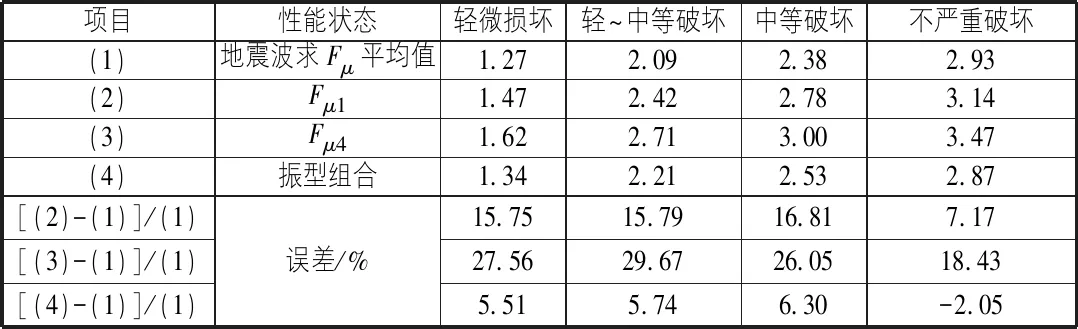
表2 Fμ计算误差对比

5 结论

1)建立非线性能量吸收因子Fμ与结构性能之间的联系，使得“抗震性能评估”的理念在核电站抗震裕度评估中得以具体化;2)从单自由度体系非线性能量吸收因子Fμ的计算出发，提出基于多模态推覆分析的Fμ计算方法；对比分析非线性时程分析与本文方法计算的Fμ的差异性；3)结构进入弹塑性状态后，高阶振型对Fμ的影响较为显著，本文提出的方法在一定程度上考虑这种影响，计算结果误差在7%以内，基本满足工程需求。