高温定向井井筒瞬态温度计算模型及其应用

郑友志 辜 涛 舒 刚 杨 谋 余 江 伍 葳 张占武 赵 军

1.中国石油西南油气田公司工程技术研究院 2.国家能源高含硫气藏开采研发中心3.“油气藏地质及开发工程”国家重点实验室·西南石油大学 4.中国石油西南油气田公司勘探事业部

0 引言

四川盆地西部（简称川西）超深天然气气井目的层埋深在8 000 m 左右，井底原始地温均大于150℃，一般都采用定向井的钻井方式钻至目的层。在常规浅井钻进时，忽略温度压力对钻井液密度与流变性影响，可确保钻进过程的顺利实施。然而，在川西超深井地层钻进时，井筒流体循环与近井壁地层发生大量热量交换，给井筒流体性能、井筒压力、井壁岩石力学性质及井下测量工具服役环境等产生重要影响。为此，准确预测川西定向井钻井过程中井筒瞬态温度，以及评价温度环境变化对流体性能与压力分布的影响就显得尤为重要。

井筒流体循环时，井筒（钻柱内流体、钻柱壁及环空流体）与地层（套管、水泥环近井壁岩石）各控制区域之间及内部的热交换方式、初始条件及边界不断发生非稳态变化[1-5]。将该热物理过程用数学模型来描述，即涉及十余个偏微分方程、十多个初始条件及二十多个边界条件联立求解。导致准确预测井筒—地层瞬态温度难度大，求解复杂。为此，部分学者为了降低其求解难度，将地层瞬态传热简化为拟稳态传热，同时，忽略了井筒内钻柱的热物理性质的作用[6-7]。分析了气井井筒温度变化[8-9]、评价了冻土原始地层温度[10]、预测了天然气水合物产量[11]以及开展了不同工况温压耦合流动计算等[12-14]。考虑到井筒—地层各控制区域传热相互耦合的机理，部分学者建立井筒一维、地层二维瞬态传热模型，采用有限差分法和有限元法对模型进行求解，研究了流体摩擦热[15]、不同机械钻速[16]、钻柱组合和井身结构[17]、地层溢流与漏失[18-20]、注入参数[21]、尾管注水泥[22]、水泥浆侯凝期间[23-25]、压裂过程[26-27]以及循环和停止循环过程对井筒温度分布的影响[28]，丰富和发展了瞬态传热模型的应用范围。然而，上述瞬态传热模型主要应用于直井的模拟计算，对于复杂结构井的模拟分析报道较少。与常规直井相比，定向井井结构包含直井段、增斜段、稳斜段等，使得钻柱组合、井眼轨迹以及井周温度的不同，引起两种井型温度预测存在较大差异。

笔者基于川西定向井的井型特征，考虑井斜角变化对井筒—地层传热机理、边界条件和初始条件等的影响，以及井筒—地层各控制区域在径向和轴向上的热交换机制，基于质量与能量守恒原理，建立了井筒—地层各控制区域二维瞬态传热模型，对模型进行空间域（轴向与径向）和时间域离散，应用高斯—赛德尔法对模型计算精度进行了判断，分析了循环时间与排量对井筒温度的影响机理，评价了温度压力耦合下井筒压力与动静态密度随井深的分布变化特征。以期为川西深井钻井井筒温度准确预测与井筒压力精细控制建立评价方法，以有助于降低井下复杂情况的发生。

1 井筒传热物理模型

井筒流体在地面以温度Tin注入，在管内向下流体过程中（vz1），取管内微元体（dz），其温度影响包括：流体与钻柱内壁面在径向上以热对流发生热交换（qpa）；流体流动时摩阻产生的热量（qpf）；以及流体从微元流入和流出热量的变化[qp(z)-qp(z+dz)]。流体到达井底，经钻头喷嘴从环空上返过程中(vz2），取环空微元体（dz），其温度变化包括：在径向上环空流体与钻柱外壁（qap）、井壁以热对流方式交换的热量（qFa）；流体流动时摩阻产生的热量（qaf）；以及流体从微元流入和流出热量的变化[qa(z+dz)-qa(z)]。该传热机理可用如图1 表示。

2 数学模型建立

2.1 摩阻压降计算

流体循环过程中，井筒—地层各区域持续发生热交换；同时，流体循环摩阻压降也会产生热量。为了计算模型压降，需要对其流动状态进行划分（层流、紊流、过渡流），根据流态计算摩阻系数，进而可获得不同流态条件下的循环摩阻压降。式（1）～（3）分别为层流、紊流及过渡流条件下的摩阻系数计算方法[29]：

式中p 表示摩阻压降，Pa；z 表示单位长度，m；ρm表示流体密度，kg/m3；f 表示摩阻系数；v 表示流体流速，m/s；d 表示等效直径，m。

图1 定向井井筒—地层传热物理模型示意图

2.2 井下传热控制方程

应用二维瞬态传热模型来描述井筒—地层间的热交换，基于能量守恒原理，则柱坐标下的能量控制方程如下：

式中T 表示温度，℃；q 表示单位面积上的热通量，J/m2；ρ 表示材料密度, kg/m3；Cp表示比热容，J/(kg·℃)；t 表示时间，s；qs表示流体流动产生的热量，J。

井筒—地层控制区域包括钻柱内流体、钻柱壁、环空流体、井壁、套管和水泥环等组成。因此，各控制区域在径向和轴向上的热通量如下：

结合式（2）和式（3），则方程（1）可表述为：

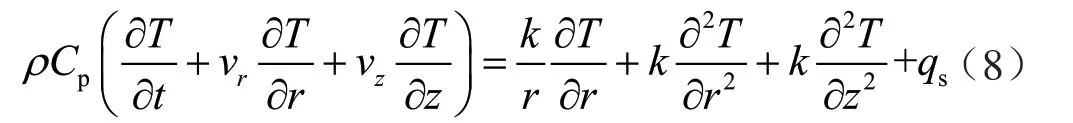
式中r 和z 分别表示圆柱坐标的径向与轴向；k 表示材料导热系数。

依据公式（8）井筒—地层控制方程，则井筒—地层各区域的传热模型与边界条件由下节叙述。

2.3 井下各区域数学模型

2.3.1 钻柱内传热模型

流体以Tin的入口温度在管内向下流动，流速为vz1；流体在向下流动过程中，与钻柱壁以热对流和热传导方式交换热量；此外，流体在流动过程中的摩阻压降会产生热量。因此，钻柱壁传热模型表述如下：

钻柱内流体与钻柱壁的边界条件可表述为：

式中T1、T2分别表示钻柱内流体和钻柱壁温度，℃；ρ1表示钻柱内流体密度，kg/m3；Cp1表示钻柱内流体比热容，J/(kg·℃)；qsi表示管内流体循环摩阻产生的热量，J； 表示钻柱内流体导热系数，W/(m·℃)；h1表示钻柱壁对流换热系数，W/(m2·℃)；r1表示钻柱内半径，m。

2.3.2 钻柱壁温度模型

钻柱内外壁流体的热对流影响着其温度，则数学模型可表述为：

则钻柱内、外壁与流体间的边界条件可用式（8）和式（9）表述：

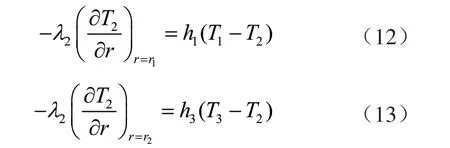
式中T3表示环空流体温度，℃；ρ2表示钻柱壁密度，kg/m3；Cp2表示钻柱比热容，J/(kg·℃)；r2表示钻柱壁外半径，m； 表示钻柱导热系数，W/(m·℃)；h3表示钻柱外壁对流换热系数，W/(m2·℃)。

2.3.3 环空流体温度模型

环空流体温度由流体流动时与钻柱外壁、井壁的对流换热及流体流动摩阻生热构成。环空传热模型可表述为：

同时，在井壁面，从地层通过热传导方式流入井筒的热等于井壁以热对流和热传导方式交换的热，则井壁边界模型可表述为：

式中vz3表示环空流体流速，m/s；qso表示环空流体循环摩阻产生的热量，J；T4表示井壁温度，℃；r3表示井壁半径，m；ρ3表示环空流体密度，kg/m3；Cp3表示环空流体比热容，J/(kg·℃)；λ3表示环空流体热传导系数，W/(m·℃)；λef表示地层有效热传导系数，W/(m·℃)；hef表示井壁对流换热系数，W/(m2·℃)；Tf表示地层温度，℃。

2.3.4 井壁周围区域热交换模型

井壁周围区域由于岩石、水泥环、套管及静止钻井液构成，其热流动以热传导方式为主。因此，近井壁地层温度模型可表述为：

式中Ti表示近井壁各区域的温度，℃；ri表示各区域径向距离，m；i 表示径向单元个数；通常大于6；(ρCp)ef表示近井壁岩石物理性质。

2.4 初始条件与边界条件

2.4.1 初始条件

2.4.1.1 给定流体入口温度

2.4.1.2 流体循环起始时，井筒内各控制区域为原始地温

式中Tin表示流体入口温度，℃；Ti,j表示井筒—地层各控制区域温度（i 表示径向方向；j 表示轴向方向），℃；Ts表示地表温度，℃；gf表示地温梯度，℃/100 m；z 表示井深，m；θ 表示井斜角，（°）。

2.4.2 边界条件

2.4.2.1 钻柱内流体、钻柱壁及环空流体在井底的温度相等

3 模型离散求解

3.1 瞬态数值模型离散求解方法

为了准确获得井筒—地层瞬态温度演变特性，需要对上述多个二阶偏微分方程联立求解，先对每个方程在空间域（径向和轴向）和时间域上离散，然后把在相同空间和时间节点的温度项进行合并，变化多个线性方程组，进而应用逐次超松驰迭代法对模型进行求解。

在时间节点t+Δt，径向r 上的隐式与轴向z 上的显示差分格式为：

在时间节点t，轴向z 上的隐式与径向r 上的显式差分格式为：

式中α、β、γ、σ、ζ 及χ 表示相关系数。

依据方程（23）、（24），把所有节点的有限差分方程用矩阵形式表述，即

3.2 温度压力耦合求解方法

图2 定向井井筒—地层瞬态传热模型求解流程图

4 计算案例分析

以川西SY132 井为例，该井目的层采用Ø149.2 mm 钻头，钻至井深7 658 m。钻井液密度为1.5 g/cm3；钻井液排量为16 L/s。钻具组合为：Ø149.2 mm PDC 钻 头+ 双 母 接 头+ 回 压 凡 尔+ 回 压 凡尔+Ø120.7 mm 钻 铤×6 根+311×HT38 转 换 接头+Ø101.6 mm 钻 杆+HT38×DS410 转 换 接 头+Ø127.00 mm 钻杆。造斜深度为6 200 m，井眼曲率为2.75°/25 m，造斜结束深度为6 450 m，保持该井斜与方位至靶点。该井井身结构与井下传热介质的热物理参数如表1、2 所示。

表1 SY132 井井身结构表

4.1 循环时间对井下温度的影响

图3 为不同循环时间条件下环空温度分布图，从图3 中可以看出，随着循环时间增加，井筒下部井段环空温度逐渐降低，均低于原始地层温度；而井筒上部井段，环空温度增加，均高于原始地层温度。导致该现象的原因为：随着循环时间增加，下部井筒的热量经流体循环携带至上部井段，使得环空温度高于上部井段的原始地层温度，地层的热量经热对流和传导方式传入地层，引起温度升高。为此，在深井钻井过程中，需要考虑循环流体对上部井段已封固段水泥环性能的影响，设计合理的水泥石养护温度，以提高井口环空水泥石的密封完整性。

表2 传热介质的热物理参数表

图3 不同循环时间下环空温度分布图

图4 为井筒流体循环10 h 时，钻柱内流体、钻柱壁及环空流体温度分布图。从图4 中可以看出，在经循环10 h 后，井筒内3 个区域在径向上温度差异不大，从图4 中的放大图可以看出，温度差约2 ℃。该现象可概况为3 方面的因素：①管内流体和环空流体在钻柱内外壁面经热对流方法交换热量，在该热交换下，管内和环空热量可经过高热传导介质钻柱迅速发生热交换；②依据井身结构与钻柱组合参数，在目的层钻进过程中，环空间隙小，循环摩阻大，促使循环摩阻产生较多热量；③目的层井底温度高达157 ℃，流体循环从下部井段携带大量热量至上部井段，增加了传热效率。

图4 循环10 h 井筒内温度分布图

图5 为循环10 h 时近井壁地层温度与环空温度之差分布图。从图5 中可以看出，下部井段近井壁地层温度高于环空温度，随着距井壁越远处，两者差值越大，表明流体循环对近井壁稳定扰动越大，近井壁温度降低越多；而上部井段近井壁温度低于环空温度，随着距井壁越远处，两者差值越小，则表明循环流体对近井壁地层加热较显著，该模拟结果更为深入的证实了在循环过程中环空流体温度演变机理。此外，在下部井段距井壁0.205 6 m 和0.292 6 m 时。地层温度发生了波动，该现象由于定向井存在造斜段与稳斜段使得井筒—地层的热交换量发生了变化。

4.2 循环排量对井下温度的影响

图6 为不同注入排量下环空温度分布图，从图中可以看出，随着排量的增加，环空下部井段温度逐渐降低。在增加相同循环排量下，井下温度降低幅度不一样。在井底，当排量从10 L/s 增加至16 L/s 时，温度降低了7.62 ℃；当排量从16 L/s 增加至22 L/s 时，温度降低了3.2 ℃。因此，针对深井钻井，在合理的排量之内可以有助于降低井下温度，若继续增加排量来降低井下温度，不仅效果不明显，还可能增加钻井成本及高排量引起井下复杂情况的发生。

图6 不同排量下环空温度分布图

4.3 井下温度压力耦合对流体性质与压力的影响

图7 流体循环10 h 时环空压力分布图

图8 循环10 h 时环空流体密度分布图

为了研究井筒温度对井筒压力的影响，分析了井筒流体循环10 h 时，在温度压力耦合作用下环空流体压力和密度分布图，如图7、8 所示。从图7 可以看出，考虑温度压力耦合和未考虑温度压力影响两种工况下，在井筒上部井段，两者循环压力几乎相等；但到了井筒下部井段，考虑温度压力耦合计算循环压力比未考虑条件下要低，且随着井深增加，两者差值逐渐增大，在井底附近两者差值最大，约为2.1 MPa。在该压力误差范围下可能引起漏失的发生。

此外，从图8 中可以看出，考虑温度压力耦合时，井筒流体静止密度和当量循环密度（ECD）均小于无温度压力作用工况下，且随着井深增加，两种工况下的密度差别越大。在井底，静止密度差值为0.065 g/cm3；ECD 差值为0.045 g/cm3。该密度误差范围将对井下流体性质判断会产生较大。因此，在深井钻井过程中，需要考虑温度压力共同作用下对井下流体性质、密度及压力的影响，以规避井下复杂风险的发生。

5 结论

1）基于动量与能量守恒原理，考虑井筒—地层各控制区域在径向和轴向上的热交换机理，建立了深井定向井井筒—地层各控制区域二维瞬态传热模型，并应用全隐式有限差分法对数学模型求解。

2）增加井筒流体循环时间和提高排量均有助于降低下部井段流体温度，但同时也提升了上部井段流体温度。在流体循环初期和最优排量下对井下温度降低幅度较大，若再增加循环时间和提高排量对下部井段温度影响较小。

3）针对流体循环会增加上部井段井壁周围的温度问题，在设计上部井段水泥石养护温度和力学性能评价时，需要考虑在钻井过程中上部井段温度高于原始温度工况下的环境温度对水泥石力学性质的影响。

4）考虑温度压力耦合下井筒流体循环压力、静止密度及ECD 均小于无温度压力条件下的值。若忽略温度压力影响，可能增加钻井复杂事故的风险。