新区块及未钻井深部地层孔隙压力预测方法——以准噶尔盆地南缘高压气井为例

霍 进 石建刚 沈新普 李 渊 沈国晓

1.中国石油新疆油田公司 2. 中国石油大学（华东）

0 引言

准噶尔盆地南缘油气田是我国正在开发中的区块[1]。其西部、东部以气藏为主，安集海区块是位于南缘油气田东部的1 个气田。该处气藏地质上具有上中下3 套生储盖组合。上部气藏开发始于20 世纪90年代末。拟开发的深部气藏垂深介于7 000～8 000 m。

地层孔隙压力预测通常基于声波和电阻率等测井数据来进行计算[2-7]，并且只能在有已钻井或者目标井邻近存在已钻井的情况下才能进行。当目标储层位于新开发的区块或者未钻井深部地层的时候，新开发区块或未钻井深部没有测井数据可供参考，其孔隙压力预测只能依靠地震波层速度[8-9]，而其钻井安全钻井液密度窗口的计算只能依靠三维地应力场的分析结果作为输入参数来进行。已有的研究成果表明[10-12]在层速度数据点采样精度须达到12 ms 以上时才能得到满足精度要求的孔隙压力预测结果。

除了层速度数据点的采样精度，影响孔隙压力预测精度的另一个重要因素是上覆岩石压力的准确度和计算精度[13]。按照孔隙压力预测的Eaton 声波计算方法，孔隙压力梯度是上覆岩石压力和声波时差的幂函数。因此，准确计算上覆岩石压力就是保证孔隙压力预测结果准确度的一个重要前提。

为此，笔者在Eaton 法中引入三维地应力和层速度来计算地层孔隙压力：首先由地震层速度计算的未钻井地层声波时差、岩石密度、最大地应力、最小地应力；然后由Gardner 经验公式法代入地震层速度计算上覆岩石压力中的岩石密度；进而对目标区块三维精细地应力场进行有限元建模计算，从而得到了目标区块的精细地应力场三维数值解，获得垂直地应力（最大主应力）、最小水平主应力，最后得到了地层孔隙压力。

1 安集河海区块概况

安集河海区块包括X7 井等多口以上部储层为目的层的已钻井，如图1 所示。区块模型的长宽分别为20.5 km、15.5 km，深度方向最大为12 000 m。平面网格尺寸为500×500 m。重点对X1 井的6 000 m以下的下部生储盖组合开展地层压力分析，包括上白垩统清水河组、下侏罗统三工河组及其下的下侏罗统八道湾组。

上部已钻的X7 井等井的目的层为古近系安集海河组和紫泥泉子组，井深介于3 000 ～4 000 m。

图1 安集海区块内3 口井的相对位置平面图及地层分布柱状图

区块内断层形式主要为逆断层和逆冲断层。这意味着区块内水平地应力分量会有较高的取值。在近地表200 ～1 000 m 深度的地层，为松散砾石层，这个范围内的地震波层速度的精度较差，如图2 所示。

从图2 可以看出，X1 井轨迹穿过的地层中，上部的地层为经历了大幅抬升的地层，这部分的地层经历了先压实、后抬升的运动，其地层的正常压实曲线的计算需要特别注意；下部地层属于原位正常压实，与上部地层的正常压实趋势曲线具有不同的斜率。具体情况需要结合上部已钻井的孔隙压力资料进行分析。

2 基于3D 地应力和层速度的孔隙压力预测原理

2.1 Eaton 法的孔隙压力计算原理

在地层孔隙压力曲线的计算中，Eaton 法是最常用的计算方法[2]，即

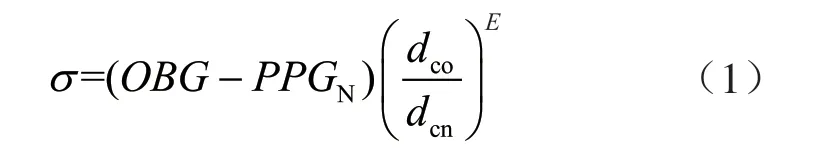
式中σ、OBG、PPGN分别表示有效应力当量密度、上覆岩石压力当量密度、地层孔隙压力当量密度，g/cm3；dco、dcn分别表示欠压实声波时差、正常压实曲线的声波时差，ms/ft（1ft=0.3 048 m）；E 表示幂指数，为根据经验、室内试件试验以及工程测量结果而取值的参数。

在Eaton 法的计算过程中，地层正常压实曲线的声波时差是和地质沉积历史相关的参数。因地质沉积历史比较复杂，而且很多时候并没有这些沉积历史信息。因此地层正常压实曲线需要根据已有钻井和钻井工程中观察到的现象来标定。

图2 过X1 井的南北与东西两个方向的地震剖面及主要断层分布图

式（1）中上覆岩石压力密度（OBG）通常由密度随深度的积分来计算确定，即

式中z 表示任意一点的深度，m；z1和z2表示地表和地层中某给定位置点的深度，z2＞z1即z2是更深的深度点；ρ(z)表示地层岩石密度，g/cm3，它是深度z 的函数。

式（2）中的岩石密度可以通过Gardner 经验公式法求得，即

式中v 表示地震波的传播速度，m/s；A 为经验系数，kg·s/m4；B 为无量纲幂指数。

当存在背斜构造且造山运动引起的水平挤压作用较为明显的时候，局部应力受构造的影响大，导致上覆岩石压力系数值与式（2）随密度积分计算得到的结果偏离较大，这时的孔隙压力预测结果的准确度将随之降低。

为了解决这个问题，我们采用了基于三维地应力场的上覆岩石压力数值计算结果作为OBG，代入到式（1）Eaton 公式，来进一步分析计算孔隙压力。这样得到的孔隙压力结果将计入背斜构造对上覆岩石压力的影响，因此，比常规的基于密度随深度积分的上覆岩石压力得到的孔隙压力计算结果要准确。

式（1）中其他参数取值为：指数E=3，正常静水压力密度PPGN=1.03 g/cm3，对于已有邻井的孔隙压力结果曲线标定所用数据为实测地层压力系数（PP）或溢流钻井液密度值等实测数据。

2.2 基于层速度和三维地应力场的孔隙压力计算流程

本文提出的孔隙压力计算流程如图3 所示，包括5 个主要的计算步骤及内容。

图3 基于3D 地应力及层速度的孔隙压力及预测流程图

由三维地震波解释构造建立地质模型是分析计算的第一步。在这一步中，采用三维地质分析软件，根据区块地震数据，来建立区块各层的地质构造。

第二步是进行邻井上部地层的单井地质力学分析。虽然深部地层没有测井数据，通过对已钻的上部地层的单井测井数据进行分析，能够得到上部地层地应力主分量的大小及方向[2-3]。

在这个分析过程中，测井数据中的声波测井的纵波及横波、密度测井等测井数据，可以用来结合实钻信息计算孔隙压力（PP）、上覆岩石压力系数（OBG）、以及岩石材料参数的值，如弹性模量（E）、泊松比、黏结强度（CS）、内摩擦角（FA）等。而地应力3 个分量中的最小水平主应力（Shmin）需要结合泊松比、弹性模量等参数来计算，并通过地漏试验来标定Shmin的计算过程中的参数取值。这个分析过程比较复杂。以使用声波测井数据计算孔隙压力这个最基本的过程为例，由于声波—孔隙压力二者之间缺乏解析函数关系，常规的做法是采用半经验—半解析的经验公式法来进行这个计算[3]。

单井地质力学分析过程中的最大水平主应力（SHmax）的取值比Shmin的取值过程要复杂很多：Shmin的取值曲线可以通过地漏试验来直接标定，SHmax的取值则无法进行这样直接的标定。工程中一般是通过采用坍塌压力（SFG）与实钻等效钻井液密度ECD曲线的匹配来间接标定最大水平主应力SHmax。这里的匹配是指坍塌压力在阻卡点要大于实钻钻井液、在没有阻卡等复杂情况的安全钻进深度点上坍塌压力要小于实钻钻井液。

上部地应力分布的特性一般和下部的地应力分布特性有关：当上部呈现逆断层应力状态时，下部地应力的横向挤压系数也会比较大。反之，当上部地应力呈现正断层应力状态时，下部的地应力的横向挤压系数也会比较小。而横向挤压效应较强烈时，由于横向变形效应的影响，上覆岩石压力的值也会比较大。

因此，在进行下部地层的地应力预测分析时，上部地层的地应力值是很好的参考资料。

第三步是根据断层形态及构造特征来确定水平构造应力系数。确定水平构造应力大小的意义是：横向挤压效应较强烈时，由于横向变形效应的影响，上覆岩石压力的值也会比较大。从而进一步导致相应的孔隙压力比较大。一般逆断层对应的最小水平主应力系数大于1，即上覆岩石压力小于最小水平主应力。而正断层对应的主应力分量中的上覆岩石压力大于最大水平主应力。

这个水平构造应力系数取值过程中，通常的做法有两个：首先是经验法，根据从具有类似构造的邻井分析中得到的构造应力系数的大小，凭经验判断目标井所在位置的构造应力系数的大小；第二个方法是试错法，即通过给定不同的构造应力系数值，观察由其得到的孔隙压力是否与实钻钻井液密度曲线相匹配。在理论方面，到目前为止，还没有一个用于从声波测井等数据来计算构造应力系数的解析公式。

第四步是进行三维精细地应力场数值求解。这里的精细是由3 个因素支持的：①基于地震波的地层构造。②基于单井地质力学分析的初始输入参数，包括孔隙压力和三个主应力分量。由于没有深部未钻地层的测井数据，单井地质力学分析仅限在上部地层范围内进行。③实测数据，包括地漏试验实测得到的最小水平主应力点、以及影像测井确认的最大水平主应力方向，这一步里，将对三维区块有限元模型施加重力载荷、初始地应力以及位移约束边界条件。

第五步为孔隙压力预测。这一步包括的内容有：①根据层速度计算地层的声波时差。②根据声波时差通过式（3）Gardner 经验公式计算地层的岩石密度。③常规做法是根据岩石密度由式（2）计算上覆岩石压力。本文的做法是通过建立区块的三维精细地应力场，进行有限元数值计算，来得到上覆岩石压力。这一步是关键的一步。④根据上覆岩石压力及声波时差，由式（1）计算孔隙压力曲线。

3 工程实例分析计算

3.1 安集海区块三维精细地应力场

3.1.1 构造模型及边界条件

三维精细地应力场建模是最近5 年来兴起的三维地应力有限元数值计算新技术[14-18]。它需要首先引入区块地震波数据来建立精确的地质模型，然后在此基础上引入已有的岩石地层测井数据来为模型提供准确的弹性模型等材料参数。

安集海区块及其中的已钻井的平面位置与地层信息已在图1 中给出。区块的地质构造模型和Abaqus有限元模型如图4 所示，有限元模型中包括370 000个节点、约90 000 个C3D20R-20 节点高精度单元。

从图4 可以看出，区块被若干条逆冲断层切割，形成的背斜构造明显。有限元模型完整继承了地层的构造。在造山运动过程中，断层部位是位移间断的位置：断层两侧位置上的切向位移间断、法向位移连续。经过了上亿年的地质时期之后，现在的应力状态主要由重力和背斜等局部构造决定。构造应力的影响还在，但是经过了上亿年的地质时期之后，构造应力的幅值已经明显减弱。在模拟断层的时候，本模型作了简化处理：断层两侧只考虑材料属性的变化、不考虑断层面本身的模拟。也就是不把断层面当成裂缝面。由于模型中只有重力载荷，而且模型是用来计算静止的当前地应力场。这个计算过程中断层两侧没有相对运动，因此这个简化是合理的。区块模型的地应力场初始值来自于X7 井的单井地应力场分析结果。在输入的时候，侧压力系数（即两个水平主应力分量和上覆岩石压力的比值）直接由单井地应力场分析结果换算过来。

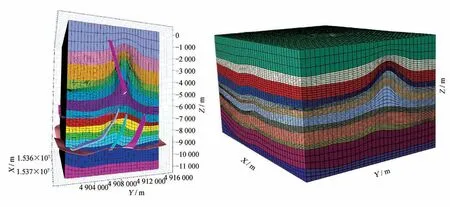
图4 安集海区块的地质构造模型和Abaqus 有限元模型图

3.1.2 邻井X7 井地应力分析

3.1.2.1 已钻地层的孔隙压力及地应力

X7 井是1 口位于安集海区块的安集海背斜顶部的直井。其目的层为安集海河组储层，图5 给出了X7 井钻遇地层及其底界深度。

图5-a 分别给出了X7 井测得的自然伽马、密度、声波时差。由于岩石密度测井数据的质量较差，分析中采用经过滤波的声波时差测井数据，使用Gardener经验式（3）的方法，重新计算了岩石密度（如图5-b蓝色曲线），用它来计算上覆岩石压力及孔隙压力等，如图5-d 所示，给出了Eaton 声波时差法得到的单井孔隙压力解析解。由于上部地层有厚度达到1 000 m的砾石层，声波时差数据的精度严重受影响。以测井纵波得到的孔隙压力在垂深2 000 m 的准确度很差。在3 100 m 深度上有一处溢流点，溢流发生时的钻井液密度为2.25 g/cm3。为此，给出了橄榄绿色的经验预测地层压力（PP）曲线，这条曲线是结合孔隙压力测量值、溢流时的钻井液密度以及孔隙压力解析解三者，综合判断得到的孔隙压力曲线，将作为接下来计算地应力场主应力曲线的依据。同时还给出了实测得到的破裂压力（LOT），但是有两个点的破裂压力密度分别达到2.65 g/cm3和2.71 g/cm3。这些值明显超过上覆岩石压力当量密度（最大值2.51 g/cm3），属于不合理的参数值。这是因为，当最小水平主应力Shmin大于上覆岩石压力（OBG）时，破裂压力就等于OBG：当达到OBG 的值的时候，地层破裂、钻井液发生漏失。

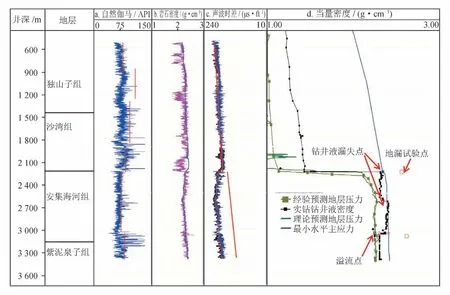
图5 X7 井的单井测井数据与孔隙压力分析结果图

钻井记录显示，在2 243 m 和2 710 m 深度上各有一个钻井液漏失点，漏失点的钻井液密度为2.48 g/cm3。在2 243 m 附近地层漏失试验。测得的漏失当量密度2.65 g/cm3（地破数据点井深2 243 m，套管鞋2 237 m，安集海河组），与钻井液漏失密度相差0.17 g/cm3。这个差别是由于在地破试验时遇到的地层的完整性较好、裂缝相对不发育，因此表现出较高的破裂压力；而在钻井过程中，在此附近遇到了裂缝发育程度高的地层位置点，导致承压能力较低，出现这个0.17 g/cm3的差别。在209 m 处的地漏实验得到的破裂压力值为2.00 g/cm3。为了得到合理的最小水平主应力Shmin的解析解，这里把破裂压力的值调整到与上覆岩石压力曲线很接近的钻井液漏失点曲线（LOT-C）数值点。最大水平主应力SHmax是通过采用1.05 构造应力系数得到的，即认为各处的SHmax/Shmin=1.05，这样的取值是一个满足实测现象的解析经验公式做法。

3.1.2.2 三维精细地应力场数值解

用上述单井地应力分析结果作为初始地应力的输入数据对X1 井研究区块精细地应力场三维建模。略去过程，直接给出区块地应力场三维有限元数值解。图6 给出了通过三维精细地应力场分析得到的X1 井的目的层侏罗系三工河组（J1s）的最大水平主应力分布图，图6-a 为三维矢量分布图，图6-b 为最大水平主应力矢量的平面投影图。由于地层起伏因素的影响，X1 井目的层的最大水平主应力分布随水平位置的变化明显。在背斜顶部的3 口井的位置上，最大水平主应力方向主要是北东—南西方向。

图6 X1 井侏罗系三工河组（J1s）精细地应力场的最大水平主应力三维和平面分布图

3.2 基于3D 地应力和层速度的X1 井孔隙压力

基于上述的三维精细地应力场数值解，就可以将地应力场在目标井轨迹点上的应力分量值提取出来、输入到Drillworks 单井地应力分析工具中，然后在给定层速度的基础上，进行X1 井基于三维地应力场的孔隙压力预测，结果如图7 所示。图7-a 为从区块地震波速度中提取的层速度，图7-b 为从地震波层速度转换来的声波时差，图7-c 紫色线为用声波数据经Gardener 经验公式计算得到的地层岩石密度，黑色曲线为至当前日期的实钻测井得到的岩石密度测井值。可以看出用声波经验公式计算得到的岩石密度比密度测井曲线数据的质量更好，也说明这一个层速度曲线是可信的。图7-d 给出了基于3D 地应力场数值解和层速度的X1 井钻井剖面的孔隙压力预测结果。图7 把X1 井位上的三维地应力场数值解转换为压力系数形式的曲线，这里只给出了最小主应力（Sminc-3D）。根据声波时差曲线与上覆岩石压力-3D曲线计算得到的孔隙压力-3D 为浅绿色的曲线；根据单井上覆岩石压力计算的孔隙压力曲线为深绿色曲线。可以看出，因为单井及三维的上覆岩石压力曲线差别不大，从而得到的两条孔隙压力曲线差别也很小。

在上部的安集海河组中，孔隙压力值介于1.20 ～2.20 g/cm3，在深度3 200 m 附近的断层破碎区，遇到钻井液漏失情况，进行了承压堵漏作业。

图7 基于3D 地应力及层速度的X1 井地层压力预测图

在下部未钻地层中的呼图壁河组至三工河组中，预测孔隙压力值介于1.90 ～2.01 g/cm3，从声波计算得到的地层强度比较高，计算得到的坍塌压力小于孔隙压力值，这个深度段的钻井液密度窗口下限取为孔隙压力值，而钻井液密度窗口的上限取最小主应力（Sminc-3D）曲线。这个最小主应力（Sminc-3D）曲线在正断层应力状态和走滑断层应力状态代表着最小水平主应力；在逆断层应力状态代表上覆岩石压力系数（OBG）。

截至2020 年11 月14 日，四开钻进至白垩系连木沁组，井深5 650 m。根据预测得到的孔隙压力分布曲线，古近系安集海河组和紫泥泉子组异常高压。实际钻井过程中，在此深度段内气测录井观测得到一定的气显示，表明此处的孔隙压力与钻井液密度接近。这表明预测孔隙压力分布曲线是准确的。

东沟组中下部地层砂岩发育，地层承压能力低，与上部地层同段钻进风险高，同时，下部白垩系胜金口组和呼图壁河组预测存在高压，因此在井深4 131 ～5 650 m 的东沟组和连木沁组采用套管专封，封隔上下高压层。计划在2021 年2 月份开始五开以后井段钻进。截至2021 年1 月份，整个钻井施工较顺利，没有遇到严重事故，说明本文的孔隙压力及三维地应力场主应力分量随深度的分布曲线是正确的，其精度满足了工程需要。

4 结论与建议

本文提出了一个基于三维地应力场和从地震波数据体中提取的层速度的方法，来预测计算未钻地层的孔隙压力。在分析三维地应力时需要单井地应力结果作为输入参数，而实钻钻井液密度曲线是计算及标定地应力分量取值的主要参考指标。通过钻井液密度曲线间接标定了孔隙压力的取值范围，以此保障孔隙压力预测值的准确性。在X1 井的钻井实践中，采用了本文给出的孔隙压力及钻井液密度窗口预测结果。与通过已钻井段取得的钻井液密度数据等工程资料相比，孔隙压力及钻井液密度实测值和预测值吻合良好，说明本文方法是实用可行的。

结合钻井实践应用效果和理论计算两个方面，需要说明的是：

1）当遇到断层破碎区的时候，由于天然裂缝的存在，尤其是高导缝的存在，虽然钻井液密度在安全窗口范围内，仍然可能发生钻井液漏失现象。这就需要进行承压堵漏操作。实践中证明了这一点。

2）基于地震波数据的声波时差数据的精度与地震波数据提取点的密度有密切关系。当地震波数据的精度不够高的时候，得到的孔隙压力预测结果的精度也会比较低。本次X1 井的例子中的地震波精度比较高，得到的孔隙压力曲线的精度能满足工程需要。

3）后续施工中得到的声波测井数据比从区块地震波数据导出的声波时差数据的精度要高。随着钻井施工的进行，不断更新完善已有声波时差数据，对整个预测计算结果的完善、保障计算结果的准确性，都有积极意义。

由于构造应力系数不仅与造山运动的历史有关，而且与局部背斜等构造有关，在三维区块的空间上其值随位置变化。这给孔隙压力的准确预测带来一定的难度，实际计算分析过程中还需要进一步研究和完善。