激光武器变焦发射系统远场光斑尺寸最小化研究与实现

张宁华,严 毅,穆学桢,谢光辉

(中国空空导弹研究院，河南 洛阳 471009)

0 引 言

自1960年世界上第一台激光器诞生[1]，激光器技术军事化应用的新概念武器研究新篇章即被开启。半个多世纪以来，随着激光技术的迅猛发展，激光武器逐渐由战略威慑走向战术运用阶段，部署平台也由地基向海、空、天平台延伸[2-4]。依靠自身的众多优势，激光武器在要地防空、巡航导弹拦截、反无人机蜂群作战、干扰致盲精确制导武器光电系统等领域均表现出了巨大的应用潜力[5-7]，各军事强国也在逐年增加经费投入，用于相关技术的突破与演示样机的开发。

作为激光武器系统重要的组成部分，发射系统的作用是发射高能激光束使其稳定辐照于目标上一段时间，最终实现对目标的有效毁伤。面对来袭的飞行目标，为了充分利用激光输出功率，缩短攻击时间，在安全距离外实施自卫拦截，需要使目标上的光斑尺寸最小，从而获得足够强的功率密度，因此发射系统需具备持续变焦能力[8-9]。虽然目前有很多关于远场变焦发射系统优化以及光束焦移的文献报道[10-12]，但对于如何获得最小辐照目标光斑及其尺度的量化研究寥寥无几。

本文以卡塞格伦共轴变焦发射系统为模型，基于高斯光束的传输规律，通过理论分析和数值仿真，对变焦范围内任一目标位置处光束半径与发射系统参数之间的关系，以及辐照目标光斑尺寸最小时发射系统离焦量与目标位置的关系进行了计算仿真研究。

1 高斯光束的光学透镜变换理论

一般情况下，激光的辐照光强呈高斯型分布，而在激光使用过程中，通常要利用光学系统对光束进行相应变换。不同于几何光学的线性理论，高斯光束的光学变换理论是非线性的，它与激光束本身的参数以及光学系统的相对位置密切相关。

描述高斯激光束的参数有很多，但在解决实际问题中使用最多的是其光斑半径大小与束腰位置的关系，即已知入射光束腰半径ω1，与光学变换系统距离z1，求经变换后的束腰半径ω2、束腰位置z2及任意位置z处的光斑半径ω3。本文研究高斯光束变换光学系统主要以透镜为主，并选择透镜前后束腰位置分别为参考面1和参考面2，其示意图如图1所示。

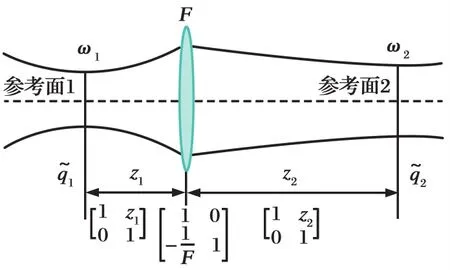
图1 高斯光束经薄透镜的变换Fig.1 Transmission of the Gaussian beam through the thin len

(1)

式中：fe1和fe2分别为高斯光束变换前后的共焦参数。高斯光束经自由空间z1、焦距为F的薄透镜、自由空间z2后，由ABCD传输变换矩阵理论，可得

(2)

(3)

联立以上各式，并令等式两端实部和虚部分别相等，可得

(4)

(5)

(6)

式(4)～(6)即为高斯光束经薄透镜后的束腰位置及光斑大小的变换关系式。由于球面反射镜的工作原理及高斯光束传输变换矩阵与薄透镜一致，因此本文将以此为基础理论进行相关计算研究。

2 卡塞格伦共轴变焦发射系统模型

与传统离轴式和透射式激光发射系统相比较，卡塞格伦共轴发射系统具有很大优势，如结构简单、大口径小筒长、成像质量高等，因此，其应用范围也更为广泛。以卡塞格伦共轴变焦发射系统为模型，对其远场光斑尺度进行定量计算分析。

根据高斯光束传输变换理论，经过卡塞格伦共轴扩束聚焦发射系统后的光束，如图2所示，其束腰光斑尺寸与聚焦距离满足如下关系：

图2 卡塞格伦共轴变焦发射系统示意图Fig.2 Schematic diagram of the Cassegrain co-axial variable- focus emission system

(7)

(8)

(9)

对于任一目标位置z处的光斑半径ω(l′,z)，可表示为

(10)

由公式(7)～(10)可知，目标位置处的光斑大小与主、副发射镜的焦点间距密切相关，即与系统的聚焦距离有关。为了探究任一目标位置处的光斑尺寸大小，联立式(7)～(8)可得

(11)

文献[15]提出，系统的聚焦距离l′在随δ的变化过程中存在一个极大值，变化曲线包括上升段和下降段两部分，因此，将l′作为已知量，通过式(8)求解δ的过程中，选择其较大根代入式(11)中，可得

(12)

将式(12)代入式(10)，可得远场光束发散角θ及目标处光斑尺寸随聚焦距离的变化关系如下：

(13)

(14)

3 聚焦距离与光斑半径的关系

假设激光发射波长λ=1.06 μm，虚束腰半径ω0=2.7 μm，主发射镜的焦距F=700 mm，β=2，系统发射口径为350 mm。根据聚焦距离l′与系统发射口径平方的正比关系[15]，l′的最大值为22.7 km。忽略传输过程中大气湍流等效应对光斑尺寸的影响，根据公式(13)～(14)，可得不同目标位置处光斑半径与远场光束发散角随聚焦距离l′的变化关系，如图3所示。

从图3可以看出，当聚焦距离由近及远靠近目标位置时，目标上光斑尺寸首先呈快速下降趋势，达到最小值后平缓上升。这是因为，当在目标位置前近距离聚焦，即紧聚焦时，聚焦光束束腰大小对聚焦距离的变化较为敏感，此时，虽然可以获取较小的聚焦光斑，但光束发散角会较大，如图3中虚线所示，因而光束发散到目标上的光斑尺寸也较大。随着聚焦距离的增加，聚焦光束束腰位置位于目标位置后，即松聚焦时，聚焦光斑变大，发散角变小，此目标上光斑尺寸的变化也趋于平缓。

图3 目标位于5 km，10 km，15 km，20 km处时，光斑半径及远场光束发散角随聚焦距离的变化曲线图Fig.3 Curves of spot radius and far-field divergence versus focusing distance with different target positions of 5 km,10 km,15 km and 20 km

此外，辐照目标的激光束的最小光斑并不是直接聚焦于该位置处的光束束腰，而是聚焦于目标前的一定位置，再发散至目标上，如图4所示。

图4 目标处最小光斑、束腰位置及系统焦距示意图Fig.4 Diagram of the minimum spot size,beam waist position and the focusing distance

产生这种现象的原因在于光束束腰半径的大小与系统的聚焦距离呈正相关性，故聚焦于目标前光束2的束腰半径要小于聚焦于目标上光束1的束腰半径，因此存在某个聚焦位置，通过发散可获得比直接聚集于目标上更小的光斑。表1列出了图3中4个不同目标位置处有关变量的具体数值。

表1 不同目标位置处的光束束腰半径与最小光斑半径Table 1 Beam waist radius and minimum spot radius at different target positions

4 最小光斑半径与离焦量的关系

为了获得目标处最小光斑与聚焦距离，即与卡塞格伦聚焦发射系统主副发射镜间距δ的关系，对式(10)作如下变换：

(15)

式中：Z=z-F。

如上所述，ω2(δ)存在一个极小值，对δ求导可得

(16)

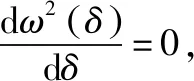
(17)

表2 不同z值对应的δ各次幂系数Table 2 Power coefficients of δ corresponding to different values of z

由表2可知，式(17)中系数c～f比a和b小两个数量级以上，因此在求解过程中可忽略，又因为δ为大于零的值，求解该式可得

(18)

式(18)表明，δ仅与目标位置和发射系统主发射镜焦距有关，与发射激光束的指标参数无关。考虑到主发射镜焦距一般在米级以下，而目标位置通常处于千米量级，二者相差三个数量级以上，因此式(18)中分母项可作近似处理。

离焦量δ随目标位置z变化的曲线图如图5所示。在图5(a)中，式(17)和式(18)所表示的曲线重合度很高，无法有效判别近似引入的两式之间的误差，因此，截取了图中14.95 km到15.0 km间的一段，如图5(b)所示。在该50 m区间内，对于某一目标位置，两式计算所得的离焦量误差在十纳米量级；对于同一离焦量，两式所对应的目标位置间距为米级，在实际使用中，离焦量的步进精度一般在微米量级，变焦精度在十米至百米量级，因此，式(17)～(18)计算结果的误差可忽略不计，即以上变换过程中进行的近似处理具有合理性。

图5 δ与z的关系曲线Fig.5 Relationship curve between δ and z

实际应用中，配合激光武器测距系统提供的目标位置信息，发射系统主副发射镜的离焦量可按式(18)设定步进程序，发射高能激光束，实现对目标持续的高功率密度辐照，精准地完成毁伤任务。

5 结 论

本文针对激光武器辐照远场目标的功率密度问题，基于高斯光束传输变换理论及卡塞格伦共轴变焦发射系统，对远场聚焦光斑尺寸进行计算评估，并对最小辐照光斑进行数值分析，结论如下：

(1) 该发射系统将激光束直接聚焦于目标上时，辐照光斑尺寸并非最小值，即功率密度并非最大。为了实现辐照光斑尺寸最小，需要将激光束聚焦于目标前的某一位置，然后通过束腰后的发散作用，来满足这一要求。

(2) 基于高斯光束传输理论，计算推导了辐照目标光斑最小时，该发射系统主副发射镜离焦量与目标位置的关系式。计算结果表明，离焦量仅与目标位置成反比关系，与系统主发射镜焦距的平方成正比，与其他参数无关。

(3) 工程实践中，可依据激光武器测距系统提供的目标位置信息作为发射伺服控制系统的输入，控制副发射镜位置精密调节器，精确控制主、副发射镜的离焦量，最终实现对目标最大功率密度的辐照。