基于多目标优化与遗传算法的公交调度模型

张荔 　冯鑫鑫 　王会龙 　张国增 　张汝峰 　刘昕伟

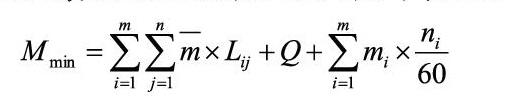
摘 要：结合地区公交现状制定合理的公交调度机制，对于公共交通发展有着重要的现实意义和指导价值。本文以公交公司运营成本和乘客出行成本最小化为目标函数，考虑车辆核载、出行时间等约束条件建立多目标优化函数，构建城市公交调度模型。然后采用遗传算法进行求解，并以黄骅市6路公交进行模型检验。研究表明，优化后的公交调度机制能够有效降低公交公司的运营成本和乘客出行的时间成本。

关键词：遗传算法 多目标优化 公交调度 调度优化

1 引言

当前我国的公交系统逐步完善，然而公交系统依然存在票价不合理、乘客满意度较低、乘客等车时间过长等问题，因此亟需构建适合地域特点的公交调度模型，实现统筹调度。本文从乘客和公交公司双重角度出发，建立多目标优化模型，并通过遗传算法进行模型求解。最后根据沧州市渤海新区地区特点、公交现状，对黄骅市6路公交车调度进行优化检验。

2 多目标优化模型建立

2.1 模型假设

由于在公交调度优化过程中需要考虑众多因素，因此对模型构建做出如下假设[1]：（1）公交车的车型统一;（2）公交车的行驶速度恒定;（3）所有公交车全程使用统一票价;（4）公交车运行过程中不考虑上下车换乘的时间。

2.2 问题分析

在实际公交运营过程中，一方面，要在满足乘客的正常出行的情况下，最大程度上减少乘客出行成本，另一方面，则需要最大可能的减少公交公司的运营成本。考虑乘客出行成本与公交公司效益，公交线路优化的具体步骤为：

步骤1：模型假设。根据公交现状数据，对模型进行初步假设，提出针对公交公司和乘客两者的分治策略;

步骤2：建立模型。基于统计数据，进行模型训练，进而构建多目标优化模型构建;

步骤3：多目标优化设计。确定影响因素以及经验数值，并结合构架完成的模型结果，构建多目标体系;

步骤4：目标函数求解。根据多目标模型，利用遗传算法对目标函数进行求解;

步骤5：检验优化结果是否为最优解，若达到优化结果，则输出优化结果，否则返回步骤1。

2.3 模型构建

2.3.1 最小公交运营成本模型

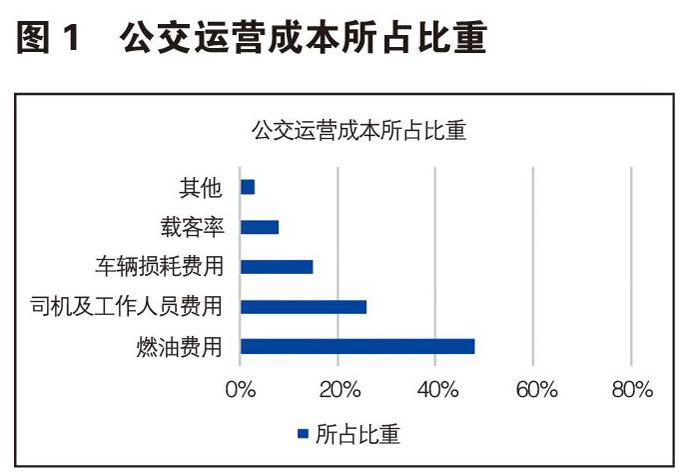
从公交公司的角度来看，公交运营成本所占比重如图1所示，决定公交运营成本的主要因素分别为：燃油费用、工作人员费用、车辆损耗费用、不同载客率影响下的产生费用。

在不妨碍乘客利益的情况下，保证主要因素费用达到运营成本的最小值，公交公司的运营成本即为最小，因此，针对以上四个主要因素建立公交最小运营成本模型：

（1）

其中，表示从站点到站点的距离;表示司机及相关人员的工资费用;表示公交平均每公里的油耗;表示一位乘客对客车造成的平均损耗;表示在站点上车的人数。

2.3.2 最小乘客出行时间成本函数模型

乘客出行成本比重如图2所示，主要分为四大阶段：出发地到公交站、等待公交、乘客上下车、上车后最终到达终点站。

针对乘客出行的四大阶段建立最小出行时间成本模型：

（2）

其中，，分别表示小区的长度、宽度;表示在站点车内的人数;表示在公交车站等待公交的时间;表示平均发车间隔，表示公交车在站点停留时间（和取经验常数）;表示乘客上下车使用的时间;表示从站点到站点的距离（）。

2.3.3 约束条件

1）出行时间约束

为了尽可能减少乘客的出行时间成本，优化过后带给乘客的出行成本一定要小于乘客常规的出行成本，即：

（3）

其中表示乘客自站上车到站下车的常规时间成本。

2）车辆核载约束

由于公交车的核载人数固定，因此车辆乘客总人数不超过车辆的核载人数，为保证公交公司的运营成本，将公交车的平均满载率约束为不低于60%。

（4）

（5）

3 模型求解

3.1 遗传算法流程

遗传算法是通过二进制或者实数编码将问题的解表示为“染色体”个体，然后进行种群初始化，對种群进行进行一系列的选择，交叉，变异操作，直至输出适应度最优的个体，得到最终结果[2]。

1）编码与种群初始化

首先，采用二进制对问题的解进行编码操作，其中每个染色体就代表在一个时间段内的发车间隔，其次，发车的时间区间共14个，针对发车间隔的特点，将客流量的时间段分为客流高峰期和客流平稳期，对于高峰期的发车间隔初始种群设置为区间[5，15]任意值，对于平稳期的发车间隔初始种群设置为区间[15，30]中的任意值。种群初始化产生随机数作为发车间隔的取值，并产生一个128bit的随机数作为初始化路线。

2）选择操作

利用公交的约束特征，对个体进行选择，随机选择个体比较，选择两者中最优的个体进入种群，重复进行操作，直至达到规定的种群数量。

3）交叉操作

针对上文使用的编码方式，通过改进交叉算子的大小来进行交叉操作。发车间隔段和路线选择段分开交叉考虑，发车间隔段以6bit为单位随机选择交叉点进行交叉，路线选择段则直接对该段所有bit选取随机交叉点交叉操作。

4）变异操作

变异是通过赋予基因较小的变异概率实现，在选取变异基因时，需要保证变化的染色体所表示的解仍然属于问题的可行解域。随机产生变异点以该bit反转作为变异点，再对该区间检查区域范围，若不符合区域范围则重新变异直至满足。

4 模型检验

4.1 基础数据

本文以黄骅市6路公交为研究对象，对此线路上各个时间段的平均每日客流量进行统计， 6路公交线总长14公里，34个站点，固定的发车间隔为15分钟，车辆的发车周期为：7：10—17：30，实行统一票价（1元/人）。由每日客流量数据分析如图3所示，将公交的发车时段分为三个阶段：客流高峰期的时间段为：7：30—8：30，17：30—19：30，客流过渡期的时间段为：13：30—15：30，客流平稳期的时间段为：6：30—7：30，8：30—13：30，15：30—17：30，19：30—20：30。

4.2 参数设计

本文使用遗传算法进行求解过程中，具体的参数设置为：初始种群数：10000高峰期为[5.15]，平稳期为[15，30];交叉率为0.5;变异率为0.01。

4.3 结果及分析

通过遗传算法求解过程，可以得到黄骅市6路公交车的优化的发车间隔，高峰期的发车间隔为9.2分钟，过渡期的优化时间间隔不发生改变依然为15分钟，平稳期的优化时间间隔为18.6分钟，考虑到公交发车时间段的实际情况一般为整数，进一步取整后得到高峰期的发车时间间隔为10分钟，平稳期的优化时间间隔为20分钟，全天发车总次数为53次，优化后的公交站点线路与公交车原线路相同。

本文针对黄骅市6路公交调度问题进行了深入的研究和优化，统计数据显示，黄骅市2路公交的日平均客流量情况与6路相仿，因此针对6路公交的优化方式同样适用于黄骅市2路公交。

5 结论

本文通过遗传算法求解多目标函数优化模型，实现公交优化调度模型构建，并对黄骅市6路公交车调度进行优化检验，研究表明，优化后的公交调度机制能够有效降低公交公司运营成本和乘客出行成本。该多目标优化调度模型及相关算法，可以推广到其他线路公交的调度问题，进而实现整个地区公交服务体系升级。

基金项目：2020年沧州市社会科学发展研究课题（动态需求下的城市公交柔性调度数学模型研究-以沧州市渤海新区为例2020025）;2020年沧州市科学计划自筹经费项目（204102004）。

参考文献：

[1]陶浪，马昌喜，朱昌锋，等.基于遗传算法的定制公交路线多目标优化[J].兰州交通大学学报，2018，037（002）：31-37.

[2]陈晓旭，项煜，杨超，等.基于遗传算法的公交线路发车间隔优化[J].交通与运输，2020（5）.