惩罚函数结合遗传算法的PID参数优化

高兴泉，黄东冬，丁三毛

(吉林化工学院 信息与控制工程学院，吉林 吉林 132022)

现如今，多数PID参数进行优化的相关优化算法在求解最优化问题时，都是依靠适应度函数值的大小来区分优化结果的好坏，可以看出目标函数的选取在优化算法中起着决定性的作用.一些常见的目标函数如绝对误差积分[1]、误差平方积分[2]、时间乘误差平方积分[3]、时间乘绝对误差积分[4]都被引用到优化算法的过程中，这些目标函数能够迅速减小起始误差，并且在系统中反应较快，但是系统中因此出现的超调变大将会无法避免，这些适应度函数作用于系统时选择性较差，最终导致系统的反应速度变慢和稳定性变差等问题.本文提出将惩罚函数[5]引入到目标函数中实现对PID的参数优化的方法，首先以传统遗传算法[6]为基础，选用时间乘绝对误差积分为目标函数，然后将系统中出现的超调量作为惩罚项来构建新的目标函数.最后以双容水箱为例的仿真结果中表明，用惩罚函数构造出的新的目标函数能大大减小超调量，提高系统的动态响应能力.

1 PID控制算法及其参数优化

PID控制器是根据系统的给定值与输出值之间的偏差作为输入信号，利用此信号来和PID控制器中的控制算法相乘产生控制输出，其控制规律如下：

(1)

其中：Kp是一个比例系数；Ki是积分系数；Kd是微分系数；e(t)是误差信号；u(t)是PID的控制输出.

PID控制器在实际应用时，最为困难的在于比例、积分、微分系数的选取问题上.所以一般都会使用优化算法对这3个参数进行优化进而得到理想的参数来应用于系统.对于传统优化算法都会使用如下4种目标函数来对参数进行优化.

对于这4种目标函数优化出来的PID参数效果并不满意，使得系统中出现震荡和超调的现象从而导致系统不稳定.这里提出将传统目标函数中结合惩罚函数的思想来解决此类问题.

2 惩罚函数

惩罚函数法[7]的优点是能将系统约束融入最优化问题中，其中心思想就是将脱离可行域的点通过构造惩罚函数的方式来进行约束，然后用最优化方法解决无约束情况下的相应的问题.然后考虑非线性约束优化问题[8-9]：

minf(x),

(2)

s.t.gi(x)≥0,i=1,…,m,

hj(x)=0,j=1,…,l,

(3)

其中f(x)为目标函数，hj(x)(j=1,…,l)是等式约束条件，gi(x)(i=1,…,m)是不等式约束条件，三者均是在Rn上的连续函数.

惩罚函数中心思想就是将问题(2)转化为：minG(x)=f(x)+cP(x)，此处的G(x)就是惩罚函数，c为惩罚因子，P(x)则为惩罚项.

通常当x在可行域内时，P(x)=0，则G(x)=f(x)；当x不在可行域内的时候，在x处，cP(x)是很大的正数，他的存在就是迫使脱离点靠近可行域.

引理2.1[10]假设f,g,h是Rn上的连续函数，对于每一个惩罚因子c，都会存在一个xc∈Rn，使得G(c)=f(xc)+cP(xc)成立，满足以下内容：

(1)inf{f(x):g(x)≤0,h(x)=0}≥

supc>0G(c)，其中G(c)=inf{f(x)+cP(x)}；

(2)当c>0时，f(x)关于x单调不降，G(c)对于c单调不降，P(xc)对于c单调不增.

为了得到满意的过渡过程动态特性，采用时间乘绝对误差积分为目标函数:

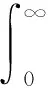
(4)

若系统中出现了超调，以原来的目标函数为基础再加入惩罚函数，将系统中出现的超调量作为惩罚项加入目标函数中形成新的目标函数：

(5)

所以对于系统中的目标函数可以总结为:

(6)

将带有惩罚函数的目标函数应用到PID的参数优化中需要一种优化算法，这里结合传统遗传算法实现PID的参数优化.

3 遗传算法解决PID参数优化问题

3.1 遗传算法

遗传算法是一种可以模拟自然界生物繁衍规则进化发展机制的随机全局搜索和优化学习算法.该算法的工作原理大致为以下3步：第1步，初始群体是在给定区域内的随机方式产生；第2步，通过研究选取的适应度函数来计算各个个体的适应度值，以适应度值的大小来判断所得解或个体是否为系统最优；第3步，按照遗传算子3大基本步骤进行寻优处理，也就是选择、交叉、变异，从而得到最优良的个体，最终让种群不断地寻优直至达到理想的目标区域内为止.

3.2 遗传算法求解PID参数优化问题的步骤

遗传算法来优化Kp，Ki，Kd3个参数，优化得到的参数对系统的控制性能有很大的改善.首先随机产生初始种群，将种群信息给予PID参数.若系统中出现超调，那么将超调量作为惩罚项构造惩罚函数并且加入目标函数中，从而生成新的目标函数.将新的目标函数融入遗传算法中的性能指标中进行判断，借助遗传算法中的基本法则不断优化，直到系统达到最大进化代数，输出最优一组参数.惩罚函数结合遗传算法优化PID参数示意图如图1所示.

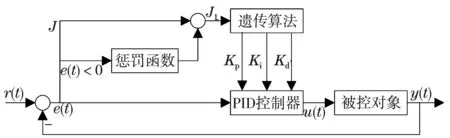
图1 遗传算法优化PID参数系统图

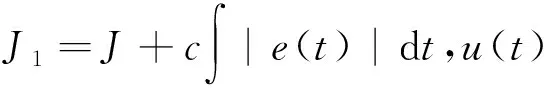
3.3 实施步骤

遗传算法通过以下步骤优化PID参数：

(1)按经验选取一组Kp、Ki、Kd参数，根据系统的实际情况以及要求确定约束条件，Kp∈[0,8]，Ki∈[0,2]，Kd∈[0,1].

(2)编码及初始种群生成.采用二进制的方法对系统中的Kp、Ki、Kd参数进行编码，并且设置种群规模为50，根据之前按经验法所得参数产生初始种群.

(3)系统如果存在超调，则选择加入惩罚函数的目标函数J1，如果没有超调，则选择目标函数J作为最优性能指标.

(4)解码，确定适应度函数f=1/J，根据适应度函数来算个体适应度值的大小来判断并找出最优个体.

(5)若符合优化要求(达到设置的最大进化代数)，即可输出系统中最优的一组PID参数，算法结束，若不满足要求，按照遗传算法的核心三大步继续寻优以寻得最优一组参数为止.

(6)返回步骤(3)，若系统流程优化至指定要求(达到设置的最大进化代数)，将最优解输出，否则，继续进行优化.

遗传算法优化PID参数的流程图如图2所示.

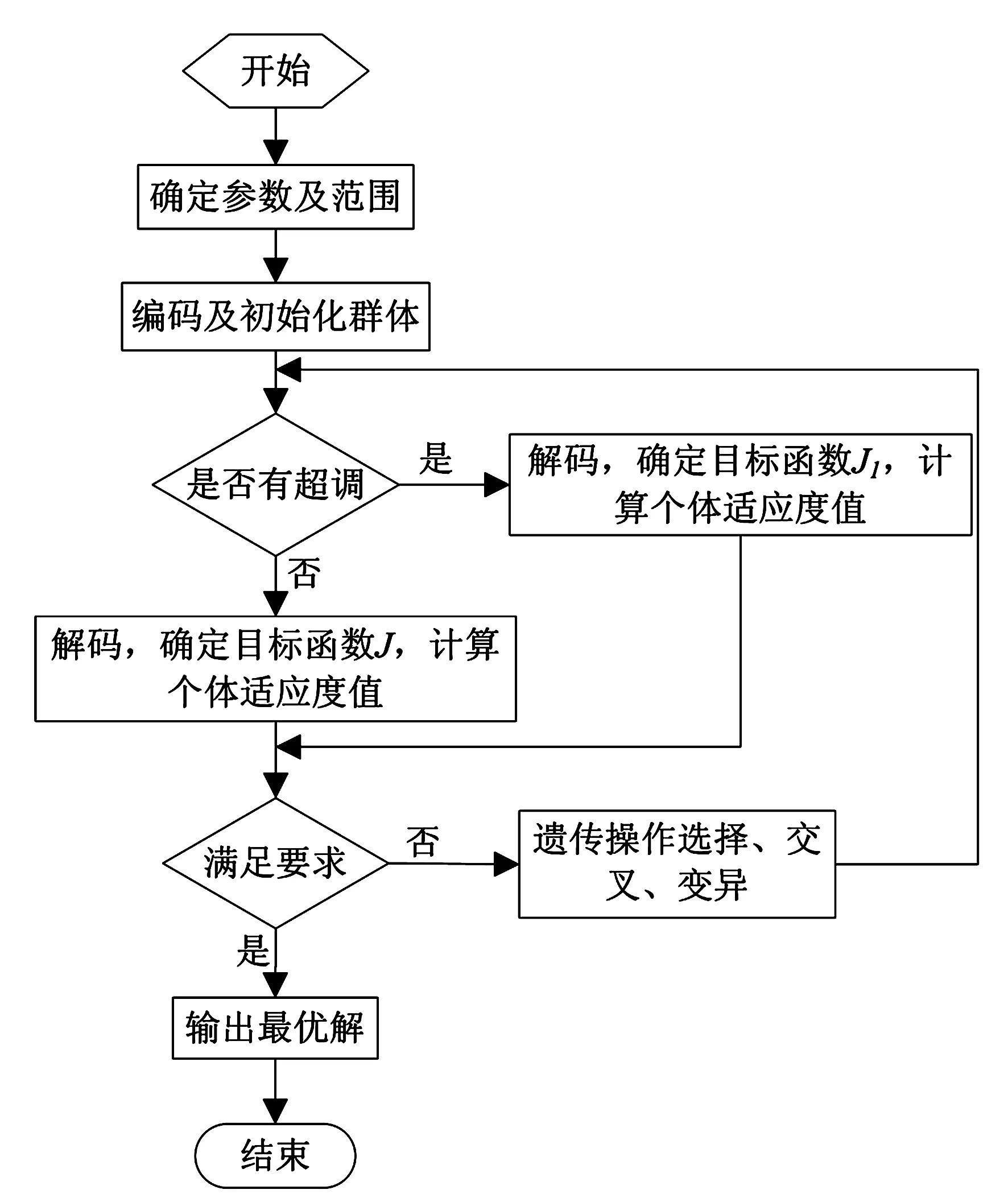
图2 遗传算法优化PID参数流程

4 仿真实验并分析

以双容水箱系统为例.将惩罚函数引入到目标函数中实现对PID参数优化的方法应用到双容水箱系统中.

双容水箱模型描述如下：

(7)

其中:h1和h2分别代表上水箱和下水箱的液位；Q代表流量；其他参数代表的意义及其数值如表1所示.

表1 参数代表意义及数值

双容水箱系统实际上是以下水箱的液位达到设定值为控制目标.上水箱和下水箱的初始液位均设为0.本次设计实验是对下水箱液位达到的设定值为15 cm.

下面采用基本遗传算法、惩罚函数引入到目标函数两种方法对PID参数整定的仿真进行对比实验.遗传算法中的种群大小设置为50，进化代数为100代，交叉率为0.9，变异率为0.01，惩罚函数的惩罚因子设置为100.

两种方法优化PID参数结果如表2所示.

表2 两种方法优化PID参数的结果

图3所示为两种优化PID参数方法对最优适应度值的对比图.

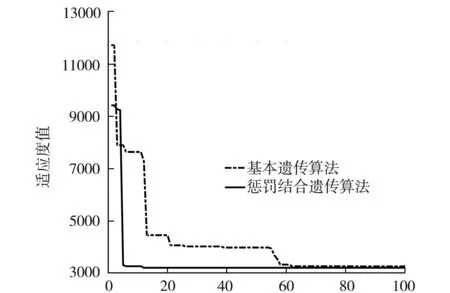
进化代数图3 最优适应度值对比图

从图3就可以看出，通过两种优化方法最后得到的最优指标几乎是一致的，但是基本的遗传算法在58代的时候接近最优，62代才能达到最优，而惩罚函数引入到目标函数的方法在5代的时候接近最优，到12代的时候就达到了最优，表明了惩罚函数引入到目标函数的方法能够大大提高系统的动态响应能力.

图4为总仿真时间为200 s下的两种优化后的下水箱液位曲线和PID输出控制量曲线.

从图4可以看出，基本的遗传算法虽然能使系统达到稳态，但是系统中还是存在着较大的超调.而用本文所设计的新目标函数的结果来看，系统中几乎没有存在超调，有效地控制了系统中的超调量，并且能够有效地改善系统控制性能的稳定性.

t/s

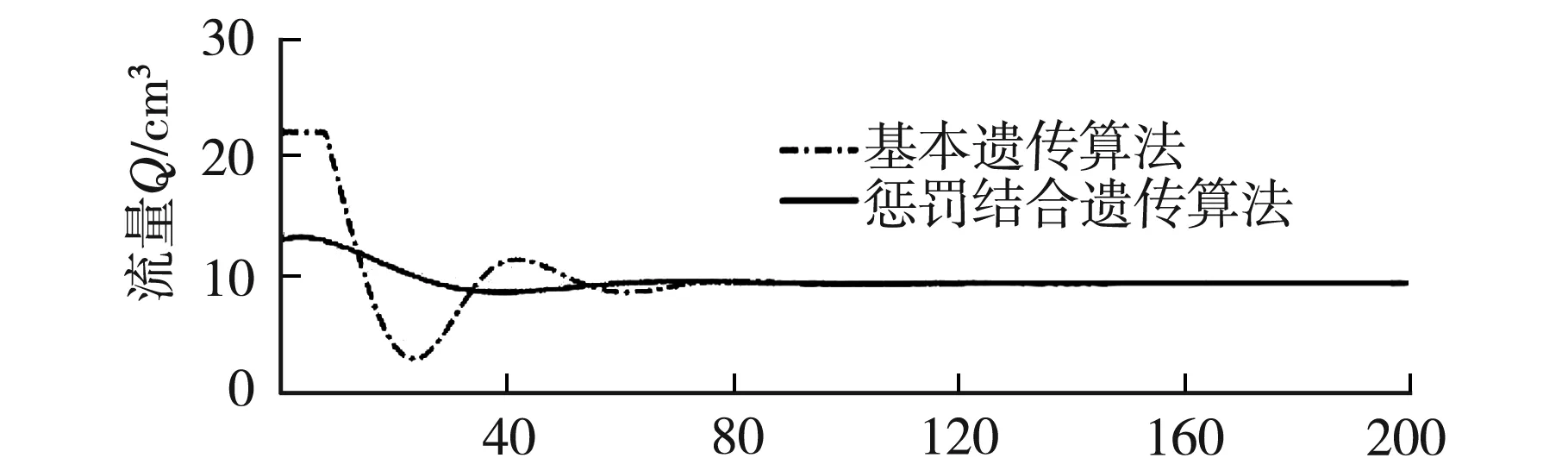
t/s图4 液位曲线及控制量曲线

5 结 论

针对传统优化算法对PID参数优化时，由于目标函数选择不当出现的超调量过大，从而引起系统的反应速度变慢和稳定性变差的问题，提出了惩罚函数引入到目标函数中实现对PID的参数优化的方法.在系统的运行过程中，一旦产生超调，则惩罚函数将会用超调量作为惩罚项加入目标函数中，进而形成新的目标函数，遗传算法将会以带有罚函数的目标函数进行优化.本文中，以双容水箱系统仿真为例，实践仿真结果表明，惩罚函数引入到目标函数中实现对PID的参数优化的方法能有效地减小了超调量，加快优化以及运行速度的同时保证了系统的稳定性.