内壳层电子对过渡金属铁熔化温度的影响

陈春彩

(闽南理工学院 大学物理教研室，福建 石狮 362700 )

过渡金属铁在第4周期第Ⅷ族，是地核的主要组成成分.因其化学性质比较活泼，能以多种同素异形体存在于自然界中.铁有多种晶体结构，常温常压下为体心立方BCC-α相结构，当温度升高到1200K时从BCC-α相过渡到面心立方结构FCC-γ相，而随着压强的增大则呈现六角密排结构HCP-ε相，低压高温下却是体心立方结构BCC-δ相等.理论和实验皆证实了以上几种晶体结构在铁的相图中能够稳定存在.但在极端高温高压条件下，铁的相图还留着一些不确定性，其高压熔化曲线还有最少2000K以上的不明区域[1].熔化是固体发生相变的一种现象，长期以来从事理论和实验研究工作的学者们对过渡金属铁的结构与相变的研究从未间断过，并得到了许多有价值的结论[1-10].卢志鹏等人用平面波赝势法研究了铁从BCC到HCP结构相变，认为铁磁性的猝灭将促使BCC结构变得不稳定而越过相变势垒向HCP结构转变[6].孙博等人用平面波赝势法研究了过渡金属铁的自旋极化总能，认为压强增加到约140 GPa时，3p电子对自旋极化总能的贡献将不能忽略[10].郑传庆等人用平面波赝势法计算过渡金属铜的自旋极化总能，通过划分不同压强下铜原子芯态和价态的关系，认为当压强增加到约139.3 GPa时，3p电子对总能的贡献将不能忽略，需将其作为价电子处理[11].

元素周期表中过渡金属铁的外层电子排布为1s22s22p63s23p63d64s2，最外层电子排布是3d64s2.通常情况下赝势法是把1s22s22p63s23p6当作内核，把3d64s2作为外壳层价电子.由于特殊的d电子轨道，决定了过渡金属铁大多数的物理化学性质.但是随着压力的递增，内层电子的影响将越来越明显.虽然第一性原理的全电子计算可以将内层电子的贡献包含在内，但计算量非常大.利用从头算的密度泛函理论平面波赝势法，能够计算过渡金属的晶格结构与能量的关系，是得到过渡金属相变熔化温度的静力学方法.该方法与全电子计算方法相比，计算量小、相对简单、能够直接描述固-液、固-固相变机理的细节.

本文基于从头算的密度泛函理论及其微扰理论，利用abinit软件包优化过渡金属Fe的能量与晶格结构的关系.研究过程中发现：计算过渡金属铁的熔化温度时应把3s23p6这8个电子看作外壳层价电子.

1 计算方法

利用从头算的密度泛函理论(DFT)及其微扰理论(DFPT)，使用程序包abinit[12]，采用广义梯度近似(GGA)，Perdew-Burke-Ernzerhof(PBE)泛函[13]和Troullier-Martins(TM)赝势完成相应的第一性原理计算.为了证实3s23p6这8个电子作为外壳层价电子对计算的影响.计算中统一采用BCC-α相铁作为研究对象.采用了统一的参数如表1所示，其中E-cut代表平面波的截断能，K-point指倒格子中对Brillouin区作Monkhorst-Pack抽样，取6×6×6能保证计算时能量可以收敛.smearing指E-cut的平滑拖尾参数，dilatmx是晶格参数的最大缩放比，spint指初始自旋极化参数，nband是能带数.

表1 优化参数

2 分析与讨论

2.1 3d64s2作最外层价电子

过渡金属铁在常温常压下是BCC结构.其外层电子排布为1s22s22p63s23p63d64s2，最外层电子排布是3d64s2.利用GGA-PBE(1996)[13]及TM赝势法，优化计算得到α-Fe磁矩为M=3.27μB，最优晶胞参数为a=0.311 388 nm，比实验测量结果a=0.286 64 nm[13]偏大8.6%.

令晶格参数[10]a=b=c，α=β=γ=90°.原胞的3个基矢分别为(x,0.5,0.5)，(0.5,x,0.5)和(0.5,0.5,x).当x=0时对应的是面心立方(FCC)结构，x=-0.25对应的是简单立方(SC)结构，x=-0.5则是体心立方(BCC)结构.经过优化计算，得到晶格能量E随原胞参数x的变化关系如图1所示.由图1可以看出x=-0.25时，SC结构最不稳定，符合实际；能量最低的位置在x=-0.48处，能量最低说明结构最稳定.根据实验相图可知，在常温常压下，α-Fe的最稳定结构应是BCC体心立方结构，即当x=-0.5时方为能量最低.显然计算结果和实验不符合.

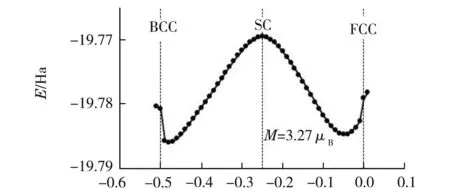
x图1 α-Fe晶格能量与原胞参数x的变化关系

考虑是交换关联能近似函数选择不恰当引起的.按交换关联函数不同分为LDA(local density approximation，局域密度近似)和GGA(generalized-gradient approximation，广义梯度近似).局域密度近似一般应用于电子密度变化相对平缓的系统，对于一些强关联体系如过渡金属、稀土金属等缺点是比较明显的.先入为主地选择了GGA进行优化计算.但是为了排除交换关联近似的影响，采用LDA和TM赝势(统一的参数如表1中的外层是8个电子情况所示)对α-Fe进行优化计算.

优化后得到常温常压过渡金属α-Fe磁矩为M=2.02μB，最优晶胞参数为a=0.280 14 nm，比实验测量结果a=0.286 64 nm[14]偏小2.3%.通过对晶胞参数的比较，显然LDA的计算结果略微优于GGA的计算结果.优化得到的晶格能量E随原胞参数x的变化关系如图2所示.由图2可知，x=-0.25时，SC结构最不稳定，符合实际.x=0时，FCC结构最稳定，这与常压下BCC结构能稳定存在的事实不符.由此，比较得出LDA比GGA更不适合用于过渡金属α-Fe熔化温度的计算.最后我们猜想有可能是在选择赝势的时候没有考虑内壳层3s23p6这8个电子对外层价电子的影响.

x图2 α-Fe晶格能量与原胞参数x的变化关系

2.2 3s23p63d64s2作最外层价电子

在考虑第3壳层3s23p6的8个电子对外壳层3d64s2电子的影响后，对 TM赝势做了适当修改.把3s23p63d64s2作为外壳层，内核只留1s22s22p6.采用GGA-PBE(1996)和修改后的TM赝势，按表1的参数再次对过渡金属α-Fe在常温常压下进行优化计算.

优化后得到常温常压过渡金属α-Fe磁矩为M=2.86μB，最优晶胞参数为a=0.297 83 nm.比Torrent等人[15]用投影平面波(PAW)方法计算得到的a=0.284 nm偏大4.9%，比实验测量结果a=0.286 64 nm[14]偏大3.9%.优化得到的晶格能量E随原胞参数x的变化关系如图3所示.容易看出x=-0.25时E=-115.622 697 6 Hatree，即SC结构最不稳定，符合实际.当x=-0.5时，E=-115.640 308 5 Hatree，即BCC结构最稳定，这与常压下BCC结构能稳定存在的实际相符.比较得出SC结构的能量比BCC结构的能量高出值ΔE=0.017 610 9 Hatree=46.24 KJ/mol.把这个能量差化成温度等于1 853 K.而1 853 K与常温常压下α-Fe的熔化温度1 811 K[14]相差2.3%，可以说是非常接近的.这与热力学理论中涨落的持续变化将引起体系发生相变的观点相符合.

x图3 α-Fe晶格能量与原胞参数x的变化关系

3 结 论

本文采用从头算的密度泛函理论及其微扰学说，使用abinit软件包平面波赝势法讨论过渡金属Fe的晶格结构与能量的关系.计算结果表明在选取TM赝势时必须考虑内壳层3s23p6这8个电子对外层价电子的影响.优化得到的晶格能量E随原胞参数x曲线符合实际，得到的熔化温度与实验结果吻合较好.认为计算过渡金属Fe的熔化温度时应考虑内壳层价电子3s23p6对外壳层价电子的影响作用.