基于实验方法的硅胶圆管柔性关节静力学研究

梁 正，裴怡杰，武广斌

(北华大学 机械工程学院，吉林 吉林 132021)

目前机器人已经广泛运用到军事、医疗、服务、娱乐、工业等各个领域,机器人已经成为人们日常生活和工作中不可或缺的一部分[1].因气动具有很高的柔性、安全性以及环境自适应性，能够减小工作过程中产生的冲击[2]，目前应用于仿生机器人、救援、探测及医疗等领域，柔性关节未来有着广阔的应用前景[3-4].柔性关节是柔性机械手的关键部件，很大程度上影响着机械手的柔顺性和运动精度[5].关节中气囊是弹性件，其静力学特性对柔性关节的运动性能起到至关重要的作用[6].

1 柔性关节结构

在工程中，橡胶产品一般不标定剪切弹性模量，而是规定橡胶的邵氏硬度HS值[7].在常用范围内，橡胶管剪切弹性模量和邵氏硬度关系可通过查表或用经验公式得到：

G=0.117e0.034HS(MPa),

(1)

橡胶最显著的物理性能就是超弹性，天然橡胶的变形量可达到600%以上[8].橡胶形变与力的关系呈现出较强的非线性[9]，拉伸率越大其非线性越明显.但在低应变区，应力与拉伸率的关系呈近似线性，条件是构件形状简单.因此，人工驱动器在使用中，当拉伸率在50%以内，橡胶管的弹性模量可近似为定值[10].

(2)

式中，E为橡胶管弹性模量；K为橡胶管体积弹性模量.

材料基本参数：高抗撕硅胶管邵氏硬度为45°，液态硅胶管邵氏硬度为32°.则利用公式可得高抗撕硅胶管剪切弹性模量为G1=0.54 MPa，弹性模量为E1=1.62 MPa，液态硅胶管剪切弹性模量为G2=0.35 MPa，弹性模量为E2=1.04 MPa.由以上参数可知，高抗撕硅胶管邵氏硬度大于液态硅胶管，则其剪切弹性模量和弹性模量均大于液态硅胶管.柔性关节结构如图1(a)所示.

(a)柔性关节三维图

(b)约束环与硅胶管实物图图1 柔性关节结构

多个形状相同紧密套装的刚性约束环嵌套在弹性硅胶管外部，见图1(b)，约束环一侧矩形孔插入板弹簧，板弹簧通过螺钉与上下端盖固定为一整体，下堵头和下端盖留有通气孔，板弹簧截面为矩形，由薄钢板制成，利用薄板的弯曲变形而起到弹簧作用，通气加压时，柔性关节向板弹簧侧弯曲变形.

2 柔性关节静力学建模

2.1 柔性关节弯曲形变角度

人工肌肉在变形过程中，硅胶管气囊的截面尺寸将发生改变.如图2所示，硅胶管外壁受约束环限制其外壁径向膨胀，外径不变，内径增大，气囊壁厚变薄.

图2 硅胶管变形前后几何关系

气囊充入气体后，关节向弹簧板一侧弯曲，其所受轴向力Fp与合力矩∑M共同作用.关节变形过程中，约束环只限制硅胶管径向变形，无施加力矩.如图3所示，经分析关节所受关节端盖处的驱动力矩Mp，板弹簧变形产生的阻抗力矩Mk以及硅胶管本身变形产生的阻抗力矩Mn.

关节上端盖处力矩平衡，可得：

Mp=Mk+Mn,

(3)

图3 关节变形所受力矩分析

当关节硅胶管气囊通入压缩气体时，关节上端盖处所产生的驱动力矩为：

(4)

式中，P为通入压缩气体气压值；L′为硅胶管中心弧线到板弹簧的距离；D1为硅胶管外径；D2为变形前硅胶管内径；l0为人工肌肉的有效长度；S为变形后硅胶管气囊内腔横截面积；Δl为关节伸长量.

关节弯曲变形时，板弹簧长宽比大，变形属于筒型弯曲，则板弹簧的弹性模量E1为：

(5)

式中，E为板弹簧材料的弹性模量；u为泊松比.

板弹簧的截面惯性矩为：

(6)

则阻抗力矩Mk、Mn分别为：

(7)

(8)

式中，E2为硅胶管的弹性模量；I2为硅胶管的截面惯性矩.其中：

(9)

将式(2)、(5)、(6)代入式(1)中，可得关节的弯曲角度θ：

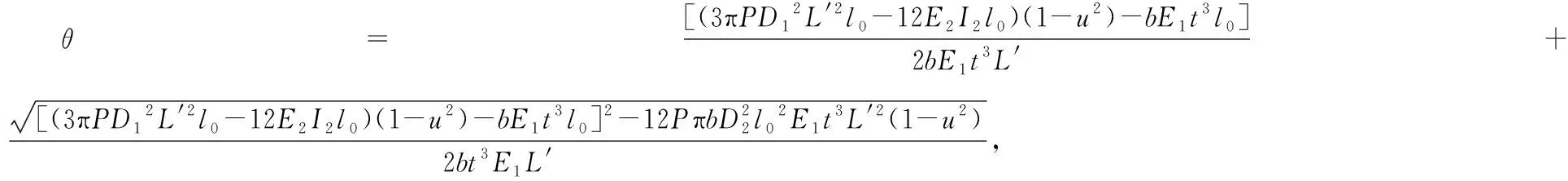
(10)

由式(8)可看出，弯曲角度θ与硅胶管弹性模量E2呈负相关.根据不同柔性关节结构，合理改变Mp、Mk以及Mn中各参数数值，都将影响关节弯曲变形程度.在弹性骨架刚度一定时，减小硅胶管气囊弹性模量可加大关节的弯曲变形；反之，弹性模量增大变形能力下降.

2.2 柔性关节夹持力

柔性关节的夹持力分析，见图4，夹持力为接触测力计限位块时产生的正压力Fn.

图4 关节夹持力分析

由关节上端盖受力分析可知:

Fpsinθ-Fksinθ-Fn=0,

(11)

Ff+Fpcosθ-Fkcosθ=0,

(12)

Mp-Mk-FfZq-FnYq=0,

(13)

(14)

(15)

式中，Fp为胶管变形产生的驱动力；Fk是关节伸长Δl时所产生的阻抗力；Fn为接触点正压力；Ff=μFn为关节与限位块接触时的摩擦力，μ为两者接触面摩擦系数，r为关节硅胶管中心到限位块的垂直距离.

通气加压过程中，由于限位块的阻碍作用，关节伸长量减少.与关节自由变形相比，关节变形受限后的伸长量Δl′与弯曲角度θ′分别为：

Δl′=kΔl,

(16)

θ′=kθ,

(17)

式中，k为关节弯曲受限时的变形协调系数，系数与关节结构和弯曲形状等有关.

因柔性关节通入压缩气体的气压值越大，外凸变形越明显.关节因自身变形内耗Mk，将减少关节的夹持力，则关节弯曲产生的阻抗力矩为：

Mk=FkL′=kFpL′,

(18)

将式(2)、式(12)～(16)代入式(11)中，得到关节正压力：

(19)

3 实验过程及分析

通过对两种硅胶管的柔性关节进行静力学实验，对比实验数据，分析不同硅胶管对柔性关节静力学性能的影响.

3.1 实验设备

实验过程中使用的实验设备由气泵、精密减压阀、数显式推拉力计、XY移动台、单片机以及陀螺仪几部分组成.关节的具体参数如表1所示.

表1 关节的参数

3.2 关节弯曲变形实验分析

将关节和陀螺仪连接在一起，然后固定在实验台上，陀螺仪与单片机和上位机相连.通入不同气压，关节弯曲变形，单片机将陀螺仪采集到的数据传输到上位机上，记录数据.实验原理如图5所示.

图5 关节弯曲变形实验原理图

将两种关节在不同气压值下的实验数据进行处理，可得到关节在不同气压下弯曲角度的变化曲线(图6).将柔性驱动器各参数代入式(10)，由图6可知，通气形变后关节弯曲角度的理论计算结果与实验数据基本吻合，说明公式的正确性.气压达到0.2 MPa时，液态硅胶管关节的弯曲角度达到了262.33°；在0.21 MPa时，关节弯曲干涉，变形受限.气压达到0.28 MPa时，高抗撕硅胶管关节的弯曲角度达到了267.6°；在0.29 MPa时，关节弯曲干涉，变形受限.柔性关节的弯曲角度随气压值的增加而逐渐增大，且呈现出一定程度的非线性，其弯曲形变形状类似圆弧状，如图7所示.

气压/MPa图6 弯曲角度-气压变化曲线

(a)高抗撕硅胶管关节(P=0.29 MPa)

(b)液态硅胶管关节(P=0.21 MPa)图7 关节弯曲角度实验图

3.3 关节夹持力实验分析

实验方法是将关节或手指一端固定，另一端可自由弯曲，将测力计固定在XY移动滑台上，调节滑台使测力计顶端与关节端盖接触，逐步提高气压值，来测量关节弯曲时的夹持力大小，测量过程均采取接触测量.实验原理如图8所示.

图8 关节夹持力实验原理图

将两种关节在不同气压值下(0～0.4 MPa)的实验数据进行处理，可得到两关节在不同气压下夹持力的对比变化曲线(图9).将柔性关节各参数代入式，通气形变后关节夹持力的理论计算结果与实验数据趋势一致，较好反映夹持力随气压的变化情况.此时，关节弯曲受限时的变形协调系数为0.50.由变化曲线可知，柔性关节接触点的夹持力随气压值的增加而逐渐增大，且呈现出一定程度的非线性.当气压值达到0.36 MPa时，液态硅胶管柔性关节夹持力达到19.62 N，继续加压，关节变形受限夹持力不再增大.在0.4 MPa时，高抗撕硅胶管关节夹持力可达17.27 N.图10为两关节夹持力实验图.

气压/MPa图9 夹持力-气压变化曲线

(a)高抗撕硅胶管关节(P=0.34 MPa)

(b)液态硅胶管关节(P=0.3 MPa)图10 关节夹持力实验图

4 结 论

通过两种硅胶管材料的性能理论计算，得到了两种不同硬度硅胶材料的剪切弹性模量和弹性模量.建立了柔性关节弯曲形变与夹持力模型，并进行了实验验证，理论计算结果与实验数据趋势相一致，气囊硅胶管弹性模量与关节弯曲角度呈负相关.实验结果表明，通入气体后，关节连续弯曲，且弯曲形变类似圆弧状.两种不同材料硅胶圆管制得关节在同一气压下，材料硬度越小，弯曲形变能力越强.两关节最大弯曲角度分别为262.33°和267.6°，最大夹持力分别为19.62 N和17.27 N，得到了弯曲角度和夹持力变化曲线，均呈非线性.