从“扑朔迷离”到“豁然开朗”——高中化学竞赛中“势箱中运动的粒子”专题

吉林

根据《全国高中学生化学竞赛基本要求》，在决赛部分有关分子结构的考查内容中有一个知识点是“一、二、三维势箱中粒子能级及对共轭体系吸收光谱的解释”，这部分内容需要较多量子力学的相关知识，对于高中生来讲，完全接受较为困难。本文尝试通过一些简单的例子让学生理解和接受相关内容并学会应用，以期为各位老师提供参考。

一、研究背景

一维势箱(阱)中粒子是指一个质量为m的粒子，在一维x方向上限制在V=0，长度为0～1的箱内运动，而箱外势能为+∞，故粒子出现在箱外的概率为0，这是一个抽象并不存在的理想模型，但有其实际意义。

如固体的许多属性(特别是电磁性质)和电子的运动状态有关，因此讨论金属中自由电子运动状态是固体理论的基本问题之一。然而要严格按照量子力学来处理实际金属的微观结构进而推算其中电子的运动状态是较为困难的。因此采取抽象的方法，把它简化为在箱中粒子运动的模型：金属中阳离子有规律的排列，电子在这种周期性的结构中自由运动，其势能也是周期性的，由于逸出功使处于金属表面的电子不能逸出到金属外面去，好像被边界上突然升高的“墙”所阻挡，在常温下金属体外电子出现的概率为0，略去势能的周期性变化，可以把金属体内自由电子的运动抽象为一个一维势箱中运动的粒子。共轭分子体系中π电子的能级近似于一维势箱体系的能级，势箱长度可以根据分子结构进行近似计算。相关量子力学推导结论如下：

直角坐标系薛定谔方程的表示形式：

如果采用球面坐标来表示其形式可以写成：

一个微观粒子的一维薛定谔方程可简化为

由周期性边界条件，即一维势箱内的势能V=0，而箱壁及箱外势能为无穷大。

经过高等数学计算(过程不需要掌握)：

进而可以得到一个非常有用的能量公式：

二、高中化学竞赛中涉及的知识点

(2)能量是量子化的，即能量总是零点能E1的n2倍，故相邻能级差为

由上式可见m、l值越小，能量差越大，只有当ml2足够小时，ΔE很大，量子化的能级才显得重要；m和l大到宏观量级时，ΔE极小，能量变化可以看作是连续的，量子效应将消失。

例如：将一个电子m=9.105×10-31kg束缚于l=10-10m的一维箱中，ΔE=(2n+1)×33.7 eV；若将一个子弹m=1 g束缚于l=10-2m的一维势阱中，ΔE=(2n+1)×3.43×10-42eV；能级差如此之小，完全可以认为能量变化是连续的，量子化是微观世界的特性之一。在一定的条件下，如果粒子的运动范围扩大了(即l增大)，相应的能量会降低，如丁二烯四个π电子能量要比乙烯两个π电子的能量的二倍要低，这使丁二烯具有更好的稳定性(即所谓的离域效应)。

(4)三维势箱中运动的粒子：

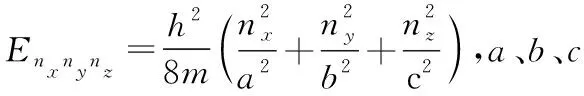
若a=b=c时，称之为立方箱或立方势阱，则方程可以变为

(5)对于一维势箱，n表示分子中双键的数目，若多烯体系C—C键的平均长度为l，两端C原子扩展半个键长，则一维势箱的长度L=2nl相关证据可参考结构化学大学教材。

(6)能量相同的能级，可能是多重简并的，此种题目难度不大，解答时应多注意基本概念和答题细节。

三、典型例题及解答

(1)12；(2)14；(3)27。

【例2】求下列体系基态的多重性：

(1)二维方势箱中的9个电子。

(2)lx=2l，ly=l的矩形二维势箱中的10个电子。

(3)三维立方势箱中的11个电子。

nx和ny取值为(1，1)时为一重简并(1，1)，能量为2E1；

nx和ny取值为(1，2)时为二重简并(1，2)或(2，1)，能量为5E1；

nx和ny取值为(2，2)时为一重简并(2，2)，能量为8E1；

nx和ny取值为(1，3)时为二重简并(1，3)或(3，1)，能量为10E1；

nx和ny取值为(2，3)时为二重简并(2，3)或(3，2)，能量为13E1；

画图表示为

nx和ny取值为(1，1)时为一重简并(1，1)，能量为5E1；

nx和ny取值为(2，1)时为一重简并(2，1)，能量为8E1；

nx和ny取值为(3，1)时为一重简并(3，1)，能量为13E1；

nx和ny取值为(1，2)时为一重简并(1，2)，能量为17E1；

nx和ny取值为(2，2)和(4，1)时为二重简并(2，2)和(4，1)，能量为20E1；

画图表示为

nx、ny和nz取值为(1，1，1)时为一重简并(1，1，1)，能量为3E1；

nx、ny和nz取值为(1，1，2)时为三重简并(1，1，2)、(1，2，1)、(2，1，1)，能量为6E1；

nx、ny和nz取值为(1，2，2)时为三重简并(1，2，2)、(2，2，1)、(2，1，2)，能量为9E1；

画图表示为

【例3】作为近似，将苯分子中π电子看作边长为350 pm的二维方势箱中运动，试计算苯分子的π电子从基态跃迁到第一激发态所吸收的光的波长。

nx和ny取值为(1，1)时为一重简并(1，1)，能量为2E1；

nx和ny取值为(1，2)时为二重简并(1，2)或(2，1)，能量为5E1；

nx和ny取值为(2，2)时为一重简并(2，2)，能量为8E1；

画图表示为

【例4】对于1，3-丁二烯，四个碳原子以sp2杂化成三个σ键后，尚余一个pz轨道和一个电子，假定下面两种情况：

(1)四个π电子形成两个定域π键。

设相邻碳原子间的距离均为l，按一维势箱粒子模型，对两种情况进行计算讨论。

这说明1，3-丁二烯中四个π电子呈离域状态时能量更低更稳定。

【例5】已知有机化合物结构如下：

已知箱长为1.30 nm，计算π电子跃迁时所吸收的光的波长。已知其实验测量值为510 nm。m=9.105×10-31kg，h=6.626×10-34J·s，c=3×108m。

【例6】(2004年化学竞赛决赛试题 第四题)日本的白川英树等于1977年首先合成出带有金属光泽的聚乙炔薄膜，发现它具有导电性。这是世界上第一个导电高分子聚合物。研究者为此获得了2000年诺贝尔化学奖。

(1)写出聚乙炔分子的顺式和反式两种构型。

(2)若把聚乙炔分子看成一维晶体，指出该晶体的结构基元。

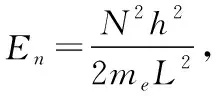
=582.0 nm。

(1)确定C60分子中的π电子个数。

(2)C60分子中的电子处于基态时，其最高占有能级的量子数L的数值是多少？

(3)根据自由电子模型，C60分子中应该有多少个未成对电子？

(4)C60电子光谱中长波部分第一吸收峰位于404 nm处，试计算C60分子的半径。

(5)已知C60在基态时无未成对电子，根据此事实必须引入二十面体的几何对称形式到自由电子的模型中来，在二十面体的环境中简并性低于球体环境，所以L=2以上的能级可分为几组，分别含1、3、4、5个简并能级，描述L=3、4、5时的能级分裂情况(无未简并的能级形成)。

(6)考虑到上述分裂情况，确定下列分子处于基态时的未成对电子的数目：

(a)K3C60；(b)K6C60。

【解析】(1)有60个π电子。

(2)由图像可知，最高占有能级的量子数L=5。

(3)根据模型应该有10个未成对电子。

(4)第一吸收峰应对应能量最低的跃迁，从L=4跃迁到L=5的空轨道上

【例8】(第44届国际化学竞赛预备题 第18题)共轭多烯π电子的能量的计算根据模型的复杂性可以得到不同的精度。最为精确的方法涉及复杂的理论手段，就是求解多粒子薛定谔方程。一个简化但仍然有效的方法就是把π电子处理为独立的“一维势箱”。这个模型对于如1，3-丁二烯这样的含共轭双键的分子的π电子能量以及电子光谱的求解而言是有效的。在这个问题中，我们使用一维势箱模型来描述乙烯以及线性和环状共轭分子的π电子组态。

能够用一维势箱模型计算出π电子能级的前提是将π电子视作能够在共轭π键长度的范围内移动的自由电子。一个含有共轭π键的无支链烃的例子是如下图所示的反-1，3，5-己三烯：

上式中，n是相应能级的量子数，其取值为1和∞之间的整数，h是普朗克常数(Js)，me是电子的质量(kg)，L是势箱长度(m)。结果保留两位有效数字。

(1)利用一维势箱模型求解：

①乙烯π电子的前两个能级的能量。

②1，3，5-己三烯π电子的前四个能级的能量。

(2)对于每一种物质，π电子的成对情况遵循泡利不相容原理。请分别求出两者的最高已占轨道的量子数n。

(3)使用最高已占轨道(HOMO)和最低空轨道(LUMO)的能级来预测上述各物质的电子从HOMO跃迁到LUMO的吸收波长。

(4)存在于胡萝卜中的一种显橙色的分子被称为β-胡萝卜素。使用一维势箱模型来计算其HOMO与LUMO之间的能量之差，利用这一能量值计算其最大吸收波长。β-胡萝卜素分子的长度为L=1 850 pm。

一些分子具有环状的共轭π体系，苯和蔻就是这些分子的典例。

对于具有环状π电子体系的分子，量子化的能级由下式给出。

在这种情况下，量子数n是介于0和±∞之间的整数，R是环的半径。与线性的势箱模型不同，环状问题允许整数n分别取正值和负值，因为等效环电流有顺时针和逆时针两个方向。此外，对于环状势箱问题，n=0是一个允许的量子态。假设苯的环半径为139 pm，蔻的环半径为368 pm。

(5)利用环状势箱模型描述苯的π电子能级。画图描述所有被电子占据以及最低空轨道的能级。在解题过程中请注意遵守泡利不相容原理，并且留意有可能有若干能态能量相同的互为简并态的能级。此外请确保你使用了正确的π电子数目。结果保留两位有效数字。

(6)仿照上一题，为蔻画出一个类似的能级图并计算所有被电子占据的轨道和最低空轨道的能量值。结果保留两位有效数字。

(7)分别计算苯和蔻的HUMO和LUMO之间的能量差。

(8)通过计算判断苯和蔲是否有颜色。推荐使用求其最大吸收波长(以纳米为单位，保留两位有效数字)的方法，假定所有分子中电子总是从HOMO跃迁至LUMO。

【解析】(1)①对于乙烯来说：

E1=7.2×10-19J；E2=4×7.2×10-19J=2.9×10-18J

②对于反-1，3，5-己三烯来说：

E1=8.0×10-20J；E2=4×8.0×10-20J=3.2×10-19J；

E3=9×8.0×10-20J=7.2×10-19J；E4=16×8.0×10-20J=1.3×10-18J；

(2)乙烯有两个π电子所以n=1是最高占有轨道，反-1，3，5-己三烯有六个π电子所以n=3是最高占有轨道。

(3)对于乙烯：

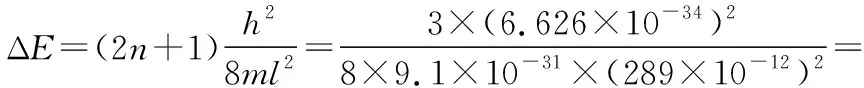
对于反-1，3，5-己三烯

(4)β-胡萝卜素的π电子能级为

共有22个电子，所以能级差为

ΔE=(122-112)×1.8×10-20=4.14×10-19J

吸收光在可见光谱区为蓝色，所以其互补色为橙黄色。

(5)苯有六个电子所以占据三个轨道n=0，±1。

E0=n2×3.2×10-19J=0 J(单重简并)

E1=1×3.2×10-19J=3.2×10-19J(二重简并)

E2=4×3.2×10-19J=1.3×10-18J(二重简并)

E1为最高占有能级，E2为最低空能级。

(6)蔻有24个电子所以占据十二个轨道n=0，±1，±2，±3，±4，±5，±6，±7。

E0=n2×4.5×10-20J=0 J(单重简并)

E1=1×4.5×10-20J=4.5×10-20J(二重简并)

E2=4×4.5×10-20J=1.8×10-19J(二重简并)

E3=9×4.5×10-20J=4.1×10-19J(二重简并)

E4=16×4.5×10-20J=7.2×10-19J(二重简并)

E5=25×4.5×10-20J=1.1×10-18J(二重简并)

E6=36×4.5×10-20J=1.6×10-18J(二重简并)

E7=49×4.5×10-20J=2.2×10-18J(二重简并)

E6为最高占有能级，E7为最低空能级。

(7)苯：1.3×10-18-3.2×10-19=9.8×10-19J

蔻：2.2×10-18-1.6×10-18=6.0×10-19J

苯的吸收在紫外区所以没有颜色，蔻的吸收接近可见光区，可以有颜色。

四、小结

通过上述例题和解析，笔者希望学习化学竞赛的学生，能对“势箱中的粒子运动”这一专题有一个较为明确的认识和较为深入的理解，并能运用相关知识解决题目中的问题。