基于蒙特卡罗的地铁车辆段工艺设备投标价格模拟

丁 俊

(福州地铁集团有限公司 福建福州 350000)

0 引言

按照中国现行的地铁车辆维修机制，一般采用一线一段一场制，即一条轨道交通线路一般配置一个车辆段、一个停车场。目前每个地铁车辆段的静态投资约为3.4亿元，一个车辆段工艺设备约480～600项，累计1000～1380台(套、辆、组)，投资概算约1亿元～1.4亿元。主要的工艺设备包括：列车清洗机、架车机、起重设备、救援设备、转向架升降台、轨道车等设备。工艺设备种类多，数量大，因此一般采用总包模式，不落轮镟床与工铁两用车、钢轨打磨车一般采用单独招标。根据2019年的中标情况，潜在投标人约55家，其中11家占据了市场份额的74.08%，市场第一的企业约占市场份额14.43%，市场竞争激烈。

价格评分一般采用合理低价法，投标文件应对招标文件提出的所有的实质性要求和条件做出实质性响应。评标委员会对满足招标文件实质性要求的投标文件按照评标价偏离评标基准价由小至大的次序推荐中标候选人。本文将以福州市轨道交通5号、4号线一期工程工艺集成一采购项目的投标数据为基础，模拟投标价格，并预测评标基准价。

1 投标报价模型

福州市轨道交通5号、4号线一期工程工艺集成一采购项目均采用综合评估法，价格分占50%，其中5号线最高限价为5500万元，4号线为5600万元。价格评分办法如下：

1.1 评标基准价确定

①当合格投标人少于五家(含五家)时，取所有合格投标人投标报价的算术平均值为评标基准价；

②当合格投标人超过五家时，去掉一个最高价和一个最低价后取剩余合格投标人投标报价的算术平均值为评标基准价。

1.2 价格得分计算

(1)投标人的投标报价与评标基准价一致的得满分100分；

(2)在投标报价高于评标基准价10%以内(含)的部分，按每高于评标基准价1%减2分，在投标报价高于评标基准价10%以上的部分，按每高于评标基准价1%减4分，减完为止；

(3)在投标报价低于评标基准价5%以内(含)的部分，按每低于评标基准价1%减0.5分，在投标报价低于评标基准价5%以上的部分，按每低于基准价1%减1分，减完为止。

按差额定率累进法计算，投标报价得分取值至小数点后2位，2位以后四舍五入。

1.3 报价规则模型

根据以上的规则，假设招标最高限价为PC，有效投标家数n，第i(i≤n)家投标人报价为Pi，评标基准价为S，第i(i≤n)家投标人价格得分Mi，由此可以得到报价规则模型。

(1)

(2)

根据式(2)可以得到图1报价得分函数，由图1可得报价得分函数是一个四分段函数。除满分情况外，同一个分数对应2个报价，即报高价策略与报低价策略。从图1可知，获得满分的条件为Pi=S。

图1 投标人报价得分函数

2 蒙特卡罗模拟

2.1 建立随机模型

本文以福州市轨道交通5号与4号线一期工程工艺集成一采购项目为例，模拟投标价格，并预测评标基准价。5号线一期工程工艺集成一采购项目最高限价5500万元，共有10家投标人参与投标。4号线一期工程工艺集成一采购项目最高限价5600万元，共有9家投标人参与投标。

本次模拟对投标报价和评标基准价同除以最高限价，以消除数据的水平和计量单位的影响。为了模拟投标情况，定义有效投标家数n，第i(i≤n)家投标人报价为Pi与最高限价PC之比PRi为输入变量，最高限价PC在招标文件中会给出，为已知变量。评标基准价S为输出变量。随机模型如下：

(3)

首先按照模型(3)建立随机模型，输入变量为n与PRi，输出变量为S。然后按照所需要的精度设置模拟次数，并利用已有的福州市轨道交通5号线以及4号线一期工程的投标数据估计n与PRi的分布，对随机变量进行随机抽取，达到指定的试验次数后进行统计分析，本文利用oracle crystal ball进行蒙特卡罗模拟，具体模拟过程如图2所示。

图2 模特卡罗模拟过程

2.2 试验次数的确定

蒙特卡罗模拟主要是利用某一事件的频率来估算概率，因此通过不断重复抽样可以使得频率无限的接近它的概率，反映到图2就是当重复次数足够大时，可以求得对用模型的真实分布情况[1]。因此，模拟计算的次数将很大程度上影响模拟结果的精度，模拟次数越多，可能的情况就越复杂，模拟结果越接近真实的分布。模拟次数可由式(4)求得。

(4)

取99.99%的置信水平，由此可确定Z0.005=2.576，取可接受的边际误差E=0.01，实践中，σ2确定的方法主要有基于历史数据、利用试验性研究、对σ值进行判断或者最优猜测[2]。本文采用利用试验性研究，即先模拟50 000次作为初始样本，以初始样本的标准差作为σ的计划值。模拟后得到初始样本的方差σ2=0.56作为计划值，计算得到m=14 425.6次。即取n≥14 426次就能保证在95%的置信水平下，边际误差为0.01的精度。因此，本文n选取为15 000次。

2.3 分布函数的假设

依据福州地铁工艺设备招标的情况，投标厂家一般不超过12家，因此n按离散分布，在3到12的自然数中随机抽取。PRi与Pi为同分布，根据Touran, Ali，Wiser, Edward P.的研究，当模型参数分布数据不足或者变化很小可采用均匀分布；如果已经最可能的费用，可采用用三角分布[3]。本文对投标厂家历史的报价与最高限价的比值PR进行拟合，并利用拟合的分布函数进行蒙特卡罗模拟。数据采用福州市轨道交通5号线以及4号线一期工程工艺集成一采购项目投标人的投标价格与各自限价的比值。由于5号线10家投标人，4号线9家投标人，投标家数较少，无法进行有效的拟合，因此这里先证明2个项目是同一个总体的2个随机抽样，再将两个样本汇总并拟合。

Kolmogorov-Smirnov检验是基于累计分布函数，用于检验一个分布是否符合某种理论分布或比较两个经验分布是否有显著差异[2]。拟合情况见图3，从检验结果来看，显著性为0.187，不拒绝原假设，可以认为两个样本来自同一分布。拟合利用oracle crystal ball软件进行，检验依然采用Kolmogorov-Smirnov检验，拟合排名第一的为韦伯分布，参数为位置-755.84，标度854.95，形状999。对应P值为0.089，不拒绝原假设，即5、4号线历史数据符合参数为位置-755.84，标度854.95，形状999的韦伯分布。

2.4 模拟结果

从模拟结果可知(图4，表1)，其频率图都为左偏，峰度均大于3表明峰的形状比较尖，比正态分布峰要陡峭。以平均值做为点估计，其概率略大于0.04，与实际的评标基准价相比，5号线预测偏差率-0.47%，4号线预测偏差率0.05%。两组预测精度较高，均能控制在0.5%以内。

图4 5号、4号线一期工程评标基准价

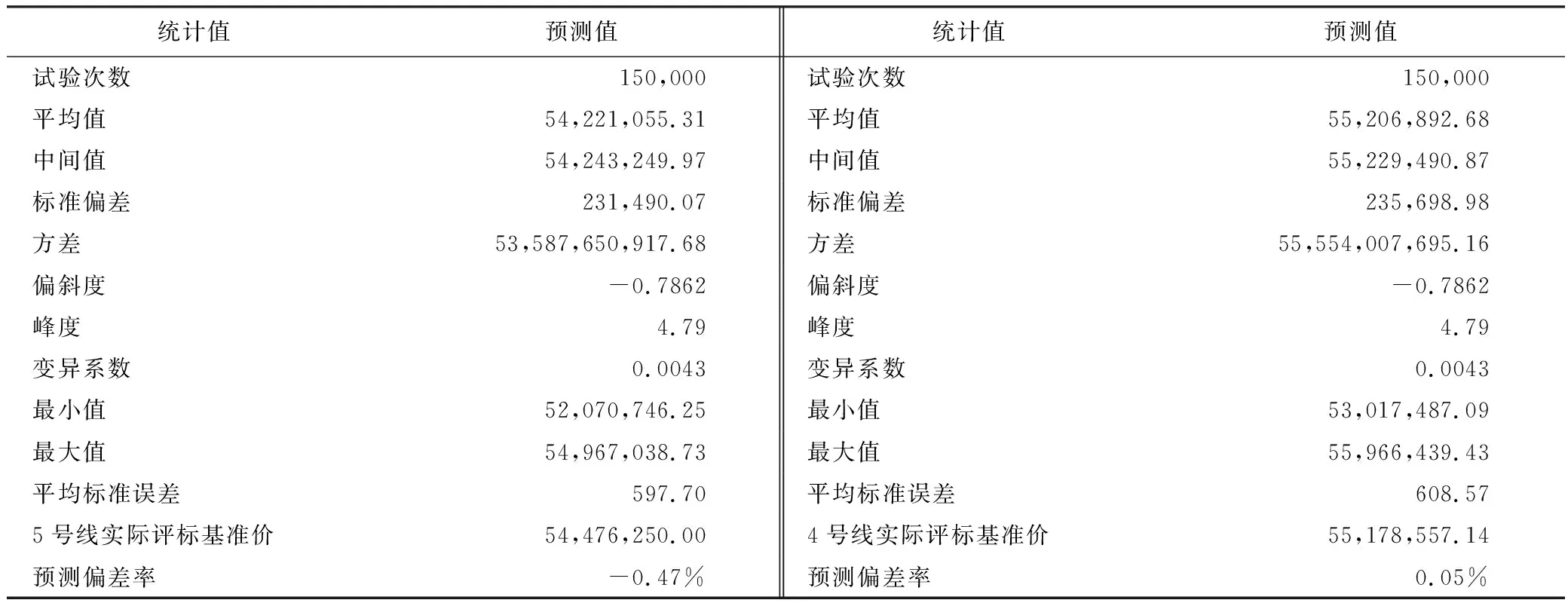
表1 预测结果

2.5 敏感性分析

为进一步了解每个参数对评标基准价的影响，利用oracle crystal ball对各个参数进行了敏感性分析，分析结果见表2。从敏感性分析的结果来看，首先，当投标厂家数n不确定时，即n从3到12随机抽取，前7家投标人的累计方差贡献已经超过了90%，也就说明7家投标人报价对评标基准价的影响已超过了90%。其次，投标厂家数n以及后3家的投标报价对评标基准价的方差贡献率非常小，均不足1%。因此，可近似认为投标家数n以及后3家投标人的报价对评标基准价无影响。最后，等级相关系数全为正数，说明投标报价与评标基准价为正相关系。

表2 敏感性分析结果

3 结论

本文利用福州市轨道交通5号线及4号线一期工程工艺集成一采购项目的投标数据，建立预测模型，进行蒙特卡罗模拟，预测评标基准价，并对影响评标基准价的参数进行了敏感性分析。结果表明利用历史数据的分布进行评标基准价的蒙特卡罗模拟能够高度接近真实的评标基准价。最高限价PC、投标人报价Pi、投标厂家数n是影响评标基准价的三个参数。在投标家数少于12家的情况下，掌握7家投标人的报价就能以94.14%的准确率来确定评标基准价。

本文的结论得出以下的启示：首先，预测依赖于信息的获取，在充分掌握对手的历史投标信息有助于提高预测的准确性。

其次，在无法确认投标厂家数的情况下，可以忽略投标厂家数n的对评标基准价的影响，即模拟时假定n为任意一个确定数，并进行模拟。牺牲一点预测的准确性，减少了未知量，为分析计算带来方便。

最后，在投标厂家数n不确定的情况下，7家的投标价格将影响超过90%的评标基准价，这就要警惕投标人组成价格联盟。投标人组成价格联盟后，商定价格，往往靠近最高限价进行报价，报价接近，价格分数集中，不具有区分度，导致价格分无法竞争。