发动机进气声衬结构参数对声激励响应的影响研究
杭超 王晨 薛东文 徐健
摘要:针对发动机进气声衬在声载荷作用下的结构设计选型需求,依次对简化的声衬有限元模型进行静力分析、模态分析和声激励分析,计算出声衬的应力分布,并通过改变声衬结构参数,研究腔深、面板厚度、孔径、蜂窝边长4种结构参数对全尺寸声衬在声激励下响应的影响规律。仿真结果表明,腔深改变引起的声衬总质量每增加1kg,声载应力减小0.484MPa;面板厚度改变引起的声衬总质量每增加1kg,声载应力减小0.105MPa;孔径和蜂窝边长对声衬质量和声载应力的影响很小。在声衬结构选型时,为了使总质量和声载应力尽量小,优先方法是增加声衬腔深,其次是增加面板厚度。
关键词:短舱声衬;声激励;模态;结构参数;有限元分析
中图分类号:V271.4文献标识码:ADOI:10.19452/j.issn1007-5453.2021.02.006
发动机进气声衬位于短舱进气道内部,通常采用比较复杂的蜂窝夹芯结构,是降低发动机噪声的重要部件[1-3]。进气声衬的设计主要考虑其吸声特性,国内外在声衬消声性能方面开展了大量研究[4-7]。由于发动机进气声衬处于高的压力脉动场中,同时承受来自进气道气流的静压力和宽频声载荷,且工作寿命需达到数十万工作小时,因此在使用中有可能发生疲劳破坏[8]。然而目前在声衬强度方面的研究还比较少。秦洁等采用试验方法研究了声衬结构在噪声和低温结冰环境下的动态性能,分析了温度、几何参数对声衬结构振动特性的影响[9]。高翔等基于载荷响应等效理论,分别进行声衬结构的噪声和振动试验,测试并计算其结构响应,给出了声衬结构在声激励和振动激励下的等效转换关系[10]。任树伟等结合理论和仿真方法研究了蜂窩层芯夹层板结构的振动特性和传声特性,分析了层芯厚度、蜂窝壁厚、夹层板面内尺寸和声压入射角度等参数对夹层板振动和传声特性的影响[11]。然而,以上研究工作都是基于平板声衬结构,采用四边简支或四边固支的边界条件,这种处理方式难以反映全尺寸环形声衬的结构特点。
本文结合周期对称边界和对称边界建立了全尺寸声衬的有限元建模,分析了全尺寸声衬结构在声载荷激励下的应力响应,探究不同结构参数对声衬响应的影响,从而给出声衬结构参数优选方法。
1声激励响应分析方法
声衬在工作环境中同时承受气流的静压力和声载荷,分析其响应需要依次进行静力分析、模态分析和声激励分析。静力分析用于计算声衬在静压力载荷作用下的位移、应变和应力。需要注意的是,进行静力分析时,需考虑声衬的几何非线性,这样可以将静载引起的声衬结构面内刚度增大引入后续分析。模态分析用于确定声衬的固有频率和振型,这是进行模态叠加法谐响应分析的基础。模态分析是一种线性分析方法,结果仅与结构的质量矩阵和刚度矩阵相关。为了获得声衬在固有频率处的响应,需求解声衬的动力学方程:

2声激励响应分析方法
2.1声衬结构有限元建模
全尺寸的短舱声衬结构尺寸非常大,且内部的蜂窝结构复杂,如图1所示,难以对全尺寸的环形声衬直接进行强度分析。考虑到全尺寸声衬具有对称性,建立18°圆心角对应的扇段进行分析,在扇段两个端面建立周期对称边界条件,同时沿长度方向取其一半,在中面上建立对称边界条件。经对称简化后声衬模型的几何大小为全尺寸模型的1/40。声衬局部几何尺寸如下:正六边形蜂窝芯边长5.5mm,芯体高度23mm。穿孔板、背板的厚度均为1.2mm,穿孔板上的小孔直径为1.2mm,小孔按等边三角形阵列均匀分布。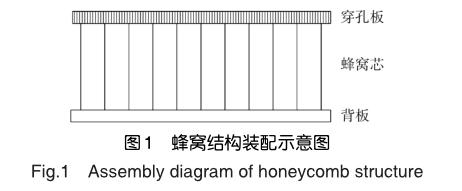
蜂窝芯材料为芳纶纸蜂窝,其密度为48kg/m3,面内弹性模量为3.1GPa,泊松比取0.2。带孔面板和无孔面板材料均为玻璃纤维/环氧树脂,其密度为2190kg/m3,面内弹性模量为21GPa,泊松比取0.16。声衬扇段模型的沿周向的两个端面为周期对称边界条件,沿长度方向一边为固支边界条件,另一边为对称边界条件,蜂窝芯与穿孔板和背板之间为Tie约束。声衬扇段模型如图2所示。
2.2声衬结构声激励仿真
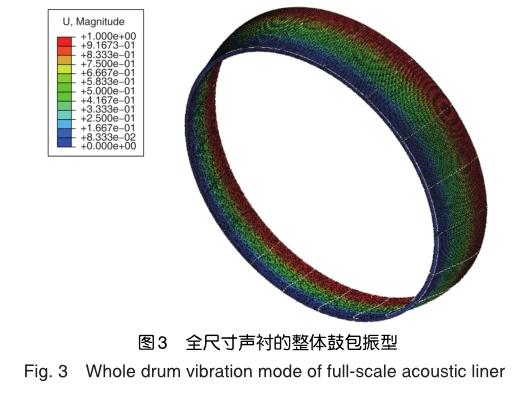
发动机短舱声衬在工作状态同时承受静载荷和声载荷。声衬背板受到垂直于表面向外的静态均布压强,大小为0.1MPa;声衬穿孔板受到垂直于表面的宽频声压载荷,频率范围为50~10000Hz,声压级范围为125~150dB。依次对声衬模型进行静力分析、模态分析和声激励分析,结果表明,环形声衬的固有频率为677.1Hz时,对应声衬的整体鼓包振型如图3所示。为了显示直观,将扇段模型中的周期对称结构全部显示出来,显示的结构为全尺寸声衬的一半。在该振型下,声衬呈现出最大应力,最大应力位置位于穿孔板对称面处,此时由声载荷引起的交变应力幅值为1.33MPa,如图4所示。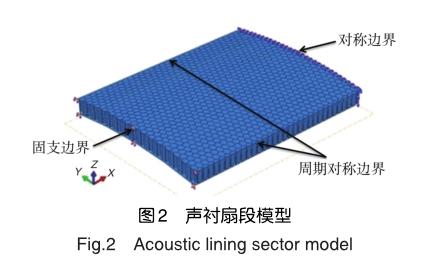
3声衬结构参数对声激励响应的影响
为了探究声衬结构参数对声载荷响应的影响,以上述典型全尺寸环形声衬模型为基础,通过控制变量法,研究腔深、面板厚度、孔径、蜂窝边长等参数对声衬响应的影响规律,从而给出声衬结构的设计选型规律。
3.1腔深对声衬响应的影响
以上环形声衬模型为原始模型,改变其腔深(即蜂窝芯的高度),其余参数不变,分别建立有限元模型,计算声衬结构在声载荷作用下的响应。原始模型中腔深为23mm,在本节中分别计算腔深为29mm、35mm、41mm三种参数的声衬响应,并与原始模型结果进行对比。表1中给出了4种腔深的声衬结构在声载荷作用下的响应。图5是声载荷引起的最大应力与腔深的关系曲线。

分析表1和图5的结果可知,随着声衬腔深的增加,声载荷引起的最大应力逐渐减小,这种减小的规律近似于线性,最大应力的位置不变。通过拟合图5中曲线可知,腔深每增加1mm,声载荷引起的最大应力减小0.009MPa。声载荷引起的应力是一种交变应力,该应力的大小对声衬结构的疲劳寿命有重要影响。从声衬强度设计的角度,增加声衬的腔深有利于提高声衬疲劳强度。
然而,增加腔深必然引起声衬总质量的增加,图6给出了改变腔深引起的声衬总质量与声载应力的关系。改变腔深,导致声衬总质量每增加1kg,声载应力减小0.484MPa。因此,在声衬设计时,需折中考虑其质量与疲劳寿命。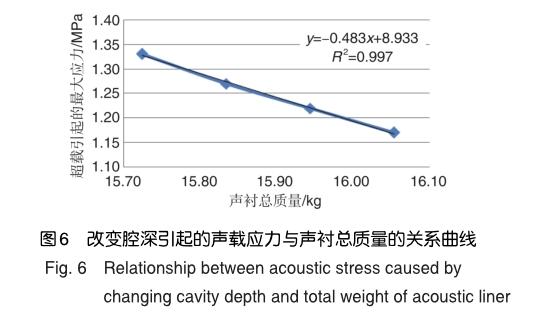
3.2面板厚度对声衬响应的影响
改变环形声衬原始模型的面板厚度(穿孔板和背板厚度相同,同时改变),其余参数不变,分别建立有限元模型,计算声衬结构在声载荷作用下的响应。原始模型中面板厚度为1.2mm,在本节中分别计算面板厚度为0.8mm、1.0mm、1.4mm三种参数的声衬响应,并与原始模型结果进行对比。表2中给出了上述4种面板厚度的声衬结构在声载荷作用下的响应。图7是声载荷引起的最大应力与面板厚度的关系曲线。
分析表2和图7的结果可知,随着声衬厚度的增加,声载荷引起的最大应力逐渐减小,这种减小的规律近似于线性,最大应力的位置不变。通过拟合图7中曲线可知,面板厚度每增加1mm,声载荷引起的最大应力减小1.36MPa。因此,增加声衬面板的厚度有利于提高声衬的疲劳强度。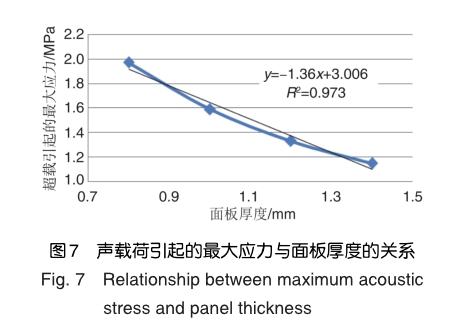
然而,增加面板厚度必然引起声衬总质量的增加,图8给出了改变面板厚度引起的声衬总质量与声载应力的关系。改变面板厚度,导致声衬总质量每增加1kg,声载应力减小0.105MPa。因此,在声衬设计时,需折中考虑其质量与疲劳寿命。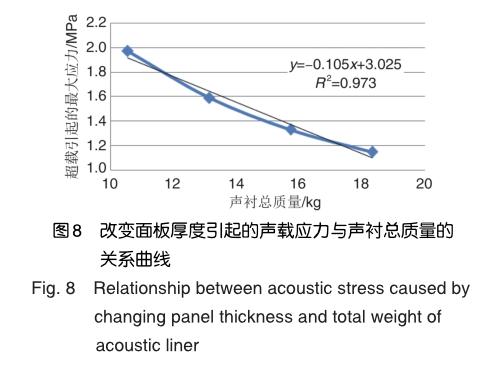
3.3孔径对声衬响应的影响
改变环形声衬原始模型的穿孔直径,其余參数不变,分别建立有限元模型,计算声衬结构在声载荷作用下的响应。原始模型中穿孔直径为1.2mm,在本节中分别计算穿孔直径为1.0mm、1.1mm、1.3mm三种参数的声衬响应,并与原始模型结果进行对比。表3中给出了上述4种孔径的声衬结构在声载荷作用下的响应。
分析表3的结果可知,随着声衬穿孔直径的增加,声载荷引起的最大应力先减小后增大,且应力变化范围很小。出现这种现象的原因是孔径改变使穿孔板的网格重新划分,网格节点位置分布发生变化,从而引起声载应力的微小改变,这也说明孔径大小对声载应力的影响不大。从声衬总质量与孔径的关系可知,孔径对声衬总质量影响非常小。因此,在声衬设计中,当孔径变化较小时,可以忽略孔径对声衬强度和质量的影响。
3.4蜂窝边长对声衬响应的影响
改变环形声衬原始模型的蜂窝边长,其余参数不变,分别建立有限元模型,计算声衬结构在声载荷作用下的响应。原始模型中蜂窝边长为5.5mm,在本节中分别计算蜂窝边长为4.0mm、7.0mm两种参数的声衬响应,并与原始模型结果进行对比。表4中给出了上述三种蜂窝边长的声衬结构在声载荷作用下的响应。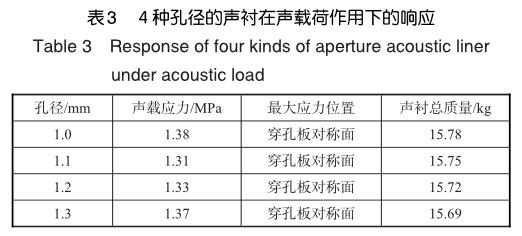

分析表4的结果可知,随着蜂窝边长从4.0mm增加到7.0mm,声载荷引起的最大应力变化很小,且没有明显的单调规律。此时,对应的声衬总质量从15.78kg减小到15.68kg,仅减小0.1kg,不到声衬总质量的1%。因为声衬的质量大部分来自于穿孔板和背板,蜂窝芯密度很小,对声衬总质量影响非常小。因此,在声衬设计中,当蜂窝边长变化较小时,可以忽略蜂窝边长对声衬强度和质量的影响。
4结论
本文基于周期对称边界和对称边界,建立了全尺寸环形无缝声衬的简化有限元模型,并分析了其在声载联合作用下的响应,最后分析了腔深、面板厚度、孔径、蜂窝边长对声衬响应的影响。
对于面板材料为玻璃纤维/环氧树脂、蜂窝芯材料为芳纶纸蜂窝的声衬结构,当4种结构参数在典型值附近变化时(典型值为腔深23mm、面板厚度1.2mm、穿孔直径1.2mm、蜂窝边长5.5mm),可以得到以下结论:综合考虑声衬质量和声载响应,腔深改变引起的声衬总质量每增加1kg,声载应力减小0.484MPa;面板厚度改变引起的声衬总质量每增加1kg,声载应力减小0.105MPa;当孔径和蜂窝边长变化较小时,可以忽略其对声衬质量和声载应力的影响。基于本文研究结果,可以给出该声衬的强度设计选型规律:为了使声衬总质量和声载应力尽量小,优先方法是增加声衬腔深,其次是增加面板厚度。
参考文献
[1]彭森.大型民用客机短舱降噪技术进展[J].科技信息, 2011(24):329-330. Peng Sen. Development of noise reduction technology for shortcabinoflargecivilaircraft[J].Scientificand Technological Information, 2011(24): 329-330. (in Chinese)
[2]梁春华,孙广华.商用飞机发动机先进降噪技术[J].航空科学技术,2011(4):48-52. Liang Chunhua, Sun Guanghua. Advanced noise reduction technology for commercial aircraft engine[J]. Aeronautical Science & Technology, 2011(4):48-52. (in Chinese)
[3]乔渭阳.航空发动机气动声学[M].北京:北京航空航天大学出版社, 2010. Qiao Weiyang. Aerodynamic acoustics of aeroengine[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010. (in Chinese)
[4]薛东文,燕群,黄文超.风扇噪声的混合数值方法研究[J].航空计算技术, 2015, 45(6): 28-31. Xue Dongwen, Yan Qun, Huang Wenchao. Hybrid numerical method for fan noise[J]. Aeronautical Computing Technique, 2015, 45(6): 28-31. (in Chinese)
[5]高翔,薛东文,燕群,等.涡扇发动机旋转声模态发生与测试试验研究[J].科学技术工程, 2018, 18(23): 128-133. Gao Xiang, Xue Dongwen, Yan Qun, et al. Research on acoustic spinning mode synthesizer and measurement of turbofan engine method validating experiment[J]. Science Technology and Engineering, 2018, 18(23): 128-133. (in Chinese)
[6]Ng C F,Zheng H. Sound transmission through double-leaf corru-gated panel constructions[J]. Applied Acoustics,1998,53:15-34.
[7]Ng C F,Hui C K. Low frequency sound insulation using stiffnesscontrolwithhoneycombpanels[J].Applied Acoustics,2007,69(4):293-301.
[8]燕群.航空發动机消声短舱强度问题浅析[N].中国航空报, 2017-08-08(5). Yan Qun. Analysis on the intensity of aeroengine short cabin[N]. ChinaAviation News, 2017-08-08(5). (in Chinese)
[9]秦洁,高翔,裴生科,等.航空发动机声衬结构低温结冰与振动噪声综合环境试验研究[J].科学技术工程, 2016, 16(2): 249-253. Qin Jie, Gao Xiang, Pei Shengke, et al. Experimental investigation on the dynamic characteristic of turbofan acoustic liner under vibro-acoustic excitation and periodic icing condition[J]. Science Technology and Engineering, 2016, 16(2): 249-253. (in Chinese)
[10]高翔,秦洁,燕群,等.发动机短舱声衬结构声振等效转换试验研究[J].强度与环境, 2015, 42(6): 29-35. Gao Xiang, Qin Jie, Yan Qun, et al. Research on equivalent conversion test method for acousticsand vibration load on engine nacelle liner structure[J]. Strength and Environment Engineering, 2015, 42(6): 29-35. (in Chinese)
[11]任树伟,辛锋先,卢天健.蜂窝层芯夹层板结构振动与传声特性研究[J].力学学报, 2013, 45(3): 349-358. Ren Shuwei, Xin Fengxian, Lu Tianjian. Vibroacoustic performance of simply supported honeycomb sandwich plates[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3): 349-358. (in Chinese)
(责任编辑陈东晓)
作者简介
杭超(1990-)男,博士研究生,工程师。主要研究方向:发动机部件强度。
Tel:029-88759513
E-mail:hangchaonwpu@163.com
王晨(1993-)男,硕士,工程师。主要研究方向:发动机部件强度。
薛东文(1987-)男,硕士,高级工程师。主要研究方向:发动机声学。
徐健(1980-)男,碩士,高级工程师。主要研究方向:发动机部件强度。
Study on the Influence of Structural Parameters of Engine Inlet Acoustic Liner on the Response of Acoustic Excitation
Hang Chao*,Wang Chen,Xue Dongwen,Xu Jian
AVIC Aircraft Strength Research Institute,Xian 710065,China
Abstract: According to the structural design and type selection requirements of the engine intake acoustic liner under the acoustic load, the static analysis, modal analysis and acoustic excitation analysis of the simplified finite element model of the acoustic liner are carried out, and the stress distribution of the acoustic liner is calculated. By changing the structural parameters of acoustic liner, the influence of cavity depth, panel thickness, aperture and honeycomb side length on the response of full-scale acoustic liner under acoustic excitation is studied. The simulation results show that the acoustic stress decreases by 0.484MPa for every 1kg increase of the total mass of the acoustic liner caused by the change of the cavity depth. The acoustic stress decreases by 0.105MPa for every 1kg increase of the total mass of the acoustic liner caused by the change of the panel thickness. The influence of the pore diameter and honeycomb side length on the acoustic lining quality and acoustic stress is very small. In order to make the total mass and acoustic stress as small as possible, the first method is to increase the depth of acoustic liner cavity, and the second is to increase the thickness of panel.
Key Words: naclle acoustic liner; acoustic excitation; modal; structural parameters; finite element analysis

