基于混合数学模型的气路静电传感器灵敏度特性分析
张寅 胡宇 孙振生 张豪 周伟



摘要:航空发动机气路颗粒物静电信号及变化规律的准确表征是实现气路静电传感器设计及静电信号监测的理论基础。针对目前静电感应数学模型简化条件不合理导致模型精度不高的问题,从棒状静电传感器结构分析出发,在推导侧面和上下底面感应电荷数学模型基础上,提出了静电感应混合数学模型,利用该数学模型对静电传感器静态和动态灵敏度进行了分析。分析结果表明,感应电荷与静电颗粒物的电荷量大小、空间位置、运动特性有关。传感器长度越长,过传感器底面投影中心方向静态灵敏度越强,在底面投影面内几乎相等;沿传感器轴线距侧面等距位置从上底面到下底面静态灵敏度先逐渐增大,然后趋于平稳,最后再减小;传感器底面直径越大,经过传感器底面投影中心方向的静态灵敏度越大;不同速度的颗粒在荷电量一致的前提下,其产生的感应电荷幅值相同,速度越快的颗粒输出信号频带越窄。运动速度快的颗粒产生的感应电荷多,其产生的感应电荷变化率的幅值随着颗粒速度的增大而增大。这将为航空发动机气路静电传感器结构优化设计和部件故障诊断提供理论基础。
关键词:航空发动机;静电传感器;数学模型;静电感应;灵敏度
中图分类号:V231.25文献标识码:ADOI:10.19452/j.issn1007-5453.2021.02.003
基金项目:国家自然科学基金重大专项(91952110);国家自然科学基金(51905540);西安市科技计划项目(201805048YD26CG32(2));陕西省自然科学基金(2020JM-359)
航空发动机内流场属于超稀相气固两相流,在燃油燃烧的过程中,将产生带电离子以及固相颗粒物,加上不完全燃烧产生的碳烟颗粒,或涡轮叶片碰摩产生的金属颗粒等一起构成了气路颗粒成分,这些气路产物在高温高压、剧烈燃烧和高速运动的条件下使颗粒物荷电[1-4]。发动机静电在线监测技术是基于静电感应原理,通过静电传感器采集航空发动机燃气中颗粒物所携带的静电信号并进行分析处理,进而为发动机及气路系统工作状态评估与健康状态在线监测提供新的方法手段[5-6]。
静电信号的准确采集与表征是实现航空发动机气路静电在线监测的基础。为实现对气路静电信号的有效采集,国内外学者设计了不同类型的静電传感器,目前主要分为侵入式和非侵入式两种类型。侵入式主要包括棒状传感器[7]和立体网状传感器[8],这些传感器结构简单,同时由于其有效敏感区域较小,将其分布在不同位置,能够有效监测到各个位置的静电信号而避免较远位置荷电颗粒的干扰,从而获取颗粒的速度及分布,但是因为与流场存在直接接触,对流场有一定的扰动;非侵入式传感器包括环状传感器[9]、阵列传感器[10]和共轴喇叭式传感器[11]等,这些传感器灵敏度较高,对流场无干扰,但是传感器采集的静电信号反映了整个发动机尾气中的颗粒荷电情况,对于气路中心区域的荷电颗粒敏感度低。
无论是侵入式传感器还是非侵入式传感器,都要求能够对整个流场内颗粒静电信号及变化规律能够尽可能地准确采集与分析,因此,需要深入理解和掌握不同传感器设计状态对流场内颗粒物静电信号采集表征的特点和规律。为了摸清颗粒静电感应的特点规律,国内外学者主要是通过建立不同类型传感器静电感应模型来进行分析。J.B.Gajewski[12],Yan Yong[13],S.N. Murnane[14]等学者建立了环状传感器的数学模型,但在这些模型建立过程中,假设绝缘层和探极电势为零不太符合实际情况,而且建立的数学模型求解也比较困难。殷逸冰[15]在此基础上对发动机吸入颗粒物进行分析时,建立了简化的环状传感器的感应模型。黄文杰[16]详细介绍了静电感应模型的建立流程,给出了点电荷在运动过程中的传感器输出的感应电压求解公式。环状传感器主要能够感应到气路中总体的静电水平,对气路中心区域灵敏度较低,主要应用在航空发动机气路颗粒物整体静电水平监测。棒状传感器存在灵敏区域小、在局部范围内灵敏度较高的特点,适用于局部静电水平监测,但可通过合理布置多个传感器实现流场区域整体静电水平的在线监测。对于棒状传感器,文振华[17]基于有限元方法,利用有限元仿真软件分析了传感器的灵敏度,但没有给出传感器感应电荷定量的具体表达式,难以对感应电荷量及影响规律进行定量分析;阚哲[18]在建立静电感应模型时将传感器简化为二维平面结构,未考虑传感器上下底面也可以产生静电感应信号,并且在计算静电感应电场强度时直接以点电荷产生的静电感应强度来替代,没有投影到垂直于传感器表面方向,因此模型计算的结果往往难以准确反映真实静电感应情况;殷逸冰[19]在建模过程中虽然考虑了侧面和一个底面的静电感应情况,但只是在特定的范围内时该情况才成立,并且对真实的静电感应情况做了一定的简化。
针对目前静电感应建模过程中存在的传感器感应面考虑不全面、感应电场强度替代不合理的问题,为了摸清静电传感器的感应特性规律,本文充分考虑了传感器表面的静电感应规律,以点电荷垂直于感应面表面的电场强度分量为变量,基于高斯定理分别推导传感器每个面的感应电荷表达式,将其叠加得到棒状传感器的混合数学模型。然后利用静电混合数学模型,通过仿真计算,分析对棒状传感器静电感应特性的影响因素,对传感器的灵敏度特性进行定量分析,为传感器的优化设计提供了理论支撑。
1静电传感器混合数学模型的建立
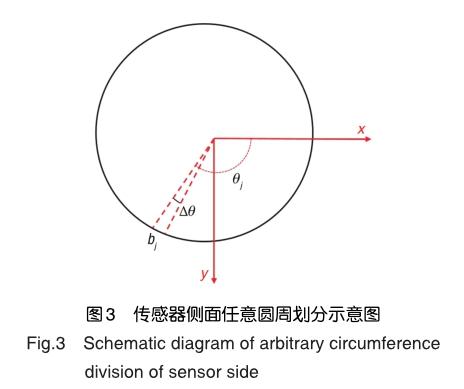
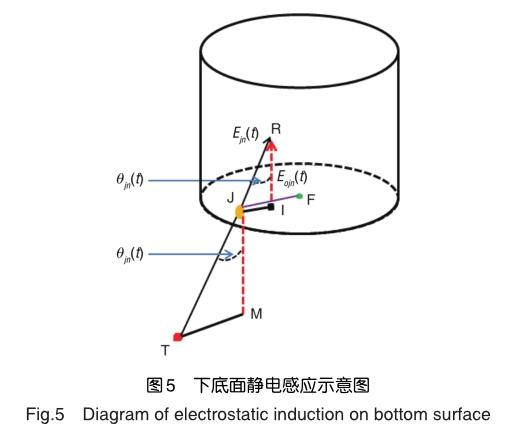
目前,航空发动机气路颗粒物在线静电监测主要分为两种方式:进气颗粒在线监测和尾流颗粒在线监测。本文主要考虑尾流颗粒在线监测这种方式,传感器类型采用棒状传感器,并建立如图1所示的坐标系,以尾喷管远点为原点,以颗粒流动方向为x轴,以水平垂直于x轴的直线为y轴。考虑到传感器探级表面均产生感应电荷,静电感应数学模型建立过程中必须考虑传感器所有感应面。根据棒状传感器结构特点,分别对侧面和上下底面进行微元划分,在利用高斯定理推导得出各个面的感应电荷表达式,最后将侧面和上下底面感应电荷表达式叠加,得到本文的混合数学模型。







2传感器灵敏度特性分析
为了验证不同颗粒物荷电特性、运动特性以及传感器形状对静电感应信号表征的影响,本文采用分析传感器灵敏度特性的方法。本文的灵敏度特性分析是基于单个带电颗粒在不同的位置以及不同的运动状态下,在传感器上感应出的电荷多少。虽然在实际的发动机尾气中,荷电颗粒物是处在不同的流态下,但是静电传感器上的感应电荷是气路流场中每一个荷电颗粒产生的感应信号的叠加,因此掌握单个荷电颗粒在传感器上产生感应电荷的规律是对不同流态下荷电颗粒产生的感应电荷分布规律进行分析的基础。所以通过分析单个电荷在传感器上产生感应电荷的能力和影响因素,就能够得到传感器感应电荷的规律和灵敏度特性。
由于气路流场的三维结构,在灵敏度分析过程中必须考虑到气路流场的空间特性与颗粒运动特点。以传感器上底面圆心为原点,竖直向下为z軸正方向建立坐标系,如图7所示。首先分析影响静态灵敏度,因为传感器是旋转对称体,那么其灵敏度空间分布也是对称的,在xoy平面上的任一点到传感器中心位置相等,其灵敏度也是相同的。因此选定荷电颗粒三个具有代表性的空间运动轨迹,来分析传感器长度和直径对灵敏度的影响规律。选定的空间运动轨迹分别是:一是沿x轴运动,轨迹过传感器中心,如图7中轨迹1所示;二是沿x轴运动,轨迹过传感器底面投影的中心,如图7中轨迹2所示;三是颗粒沿z轴方向运动,如图7轨迹3所示。下面分别对静电传感器的静态灵敏度和动态灵敏度进行分析。
2.1传感器静态灵敏度特性分析
传感器静态灵敏度的影响因素主要是传感器本身的长度和底面直径等,因此结合本文提出的混合数学模型,分别从传感器长度和底面直径分析对灵敏度的影响。
(1)传感器长度对静态灵敏度影响
选取长度为4cm、8cm、10cm,直径为1.6cm的传感器为研究对象,传感器灵敏度仿真结果如图8~图10所示。图8为荷电颗粒沿平行于x轴方向沿传感器中心线运动时,各个点位的灵敏度。图8表示当颗粒从x=0.8cm处即传感器表面由近到远时运动时,其灵敏度逐渐减小,不同长度传感器总体变化趋势相同,长度较短的传感器灵敏度变化速率较快。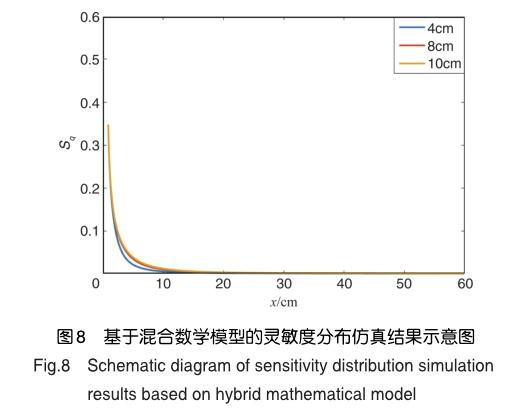
图9为荷电颗粒沿距底面1cm、平行于x轴方向运动时灵敏度分布情况,不同长度传感器灵敏度变化的总体趋势是随着距离传感器距离由远及近再变远,灵敏度先变大再减小,在传感器正下方时,各个长度传感器在此位置达到灵敏度峰值。不同长度的传感器相比而言,长度较长的传感器,相对于长度较短的传感器在同一位置处具有较高的灵敏度。
图10给出了颗粒由传感器下底面运动到上底面过程中传感器灵敏度变化情况。运动时颗粒到传感器表面距离为1cm,传感器底面直径不变时,随着传感器长度加长,在距离传感器表面相同位置处的灵敏度分布逐渐平稳,随着传感器长度变大传感器灵敏度的平稳区域逐渐变大。
图11表示荷电颗粒在通过距下底面1cm处时,传感器上底面、侧面、下底面等三个面产生的灵敏度对比图。三个面的灵敏度都是随着x先增大再下降,灵敏度变化率在-5~0cm之间时,下底面增长最快,侧面次之,底面最慢。灵敏度在传感器底面中心位置达到最大值,下底面为0.11,侧面为0.034,上底面为0.009。从图9~图11的对比可以看出,在荷电颗粒分别距底面和侧面1cm处运动时,荷电颗粒在不同空间轨迹运动时,传感器各个表面都会因静电感应而产生荷电。当荷电颗粒沿x方向通过传感器下底面时,下底面的灵敏度大于侧面和上底面。因此在建立传感器静电感应数学模型时,考虑传感器底面的静电感应是十分必要的。
(2)传感器底面直径对灵敏度影响
选取底面直径为0.4cm、0.8cm、1.6cm,长度为8cm的传感器进行分析,分析结果如图12和图13所示。图12给出了荷电颗粒沿过传感器中心线平行于x轴运动,从贴近传感器侧面到远离传感器侧面的过程中,灵敏度逐渐降低。

圖13给出了颗粒沿距底面2cm平行于x轴方向运动时,传感器各点灵敏度变化情况。在其他条件保持一致的前提下,随着底面直径增大,传感器灵敏度就越大。
图14和图15给出了不同底面直径下,距离传感器侧表面1cm、2cm处灵敏度随传感器长度变化情况,当传感器长度达到一定大小后传感器在该位置的灵敏度不再发生明显改变。因此可以通过这一结论确定传感器的最优长度应大于8cm。而最优直径的确定可以通过粒子群优化算法,在确定最优长度之后,寻找最优长径比,结合传感器对流场的影响,来确定最优直径。综上所述,气路静电传感器长8cm、直径3.8mm时,能够获取最有效的颗粒静电感应信号,这为气路传感器结构优化设计提供有效理论方法。

2.2传感器动态灵敏度特性分析
前面分析了传感器的结构尺寸对静态灵敏度的影响,但是不同的荷电颗粒物和颗粒物具有的不同的运动特性也会影响到传感器的信号输出,因此需要从颗粒特性和运动特性运动的角度来对传感器对颗粒静电感应信号分辨能力进行仿真分析,及对传感器动态灵敏度进行仿真分析。
在进行仿真时,传感器长度设为8cm,底面直径为0.8cm,假设颗粒荷电量相同,均为1C,颗粒以不同的速度经过距离传感器下底面1cm处,其感应电荷变化情况如图16和图17所示,不同速度的颗粒在荷电量一致的前提下,其产生的感应电荷幅值并未发生改变,但频带宽度发生明显变化,即速度越快的颗粒其频带越窄;图16为电荷变化量随时间变化图,速度较低的荷电颗粒其电荷变化率幅值较低,频带较宽,速度越大,其幅值越大,变化越剧烈。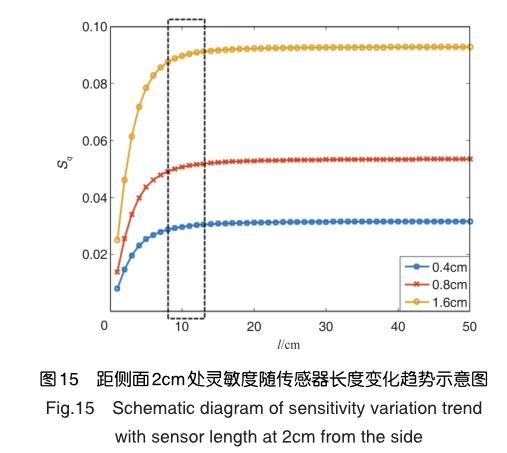
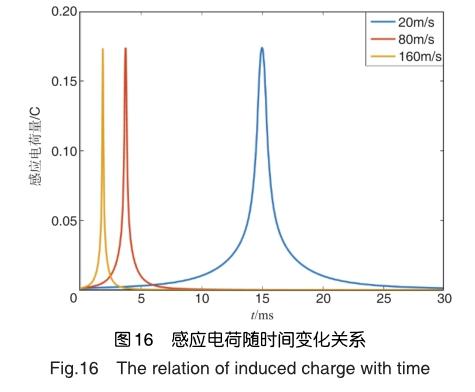
实际上在相同的流场条件下,不同颗粒种类和颗粒直径将会直接导致其荷电量有所差异,颗粒运动速度也会有所不同。通过前期仿真分析,颗粒直径100μm时,运动速度大约为20m/s;颗粒直径约为40μm时,运动速度大约为80m/s;颗粒直径约为10μm时,运动速度是大约为160m/s;设10μm的颗粒荷电量为1C时,20m/s、80m/s的颗粒对应的荷电量依次为4C、10C[17]。通过混合数学模型进行计算得到单个电荷运动过程中电荷量及其变化率与时间关系如图18和图19所示。
从图18可知,颗粒荷电量越多,产生的感应电荷越多。从图19可以明显看出,感应电荷越多,其感应电荷变化率的幅值不一定越大,它还取决于颗粒本身运动速度。但是速度越大,电荷变化率的频带越宽的规律保持不变。因此,根据静电信号对不同直径颗粒物判别,需要综合荷电量和速度两个因素进行分析,这为航空发动机气路颗粒物判别以及部件故障分析提供了有效的方法依据。

3结论
为了实现对静电传感器感应特性的表征,本文对棒状静电传感器进行了研究,建立了混合数学模型,得到了以下结论: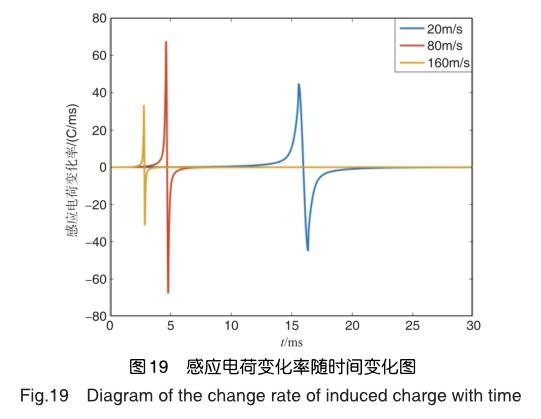
(1)针对静电感应模型简化条件不合理导致模型精度不高的问题,结合棒状静电传感器结构分析,提出了静电感应混合数学模型,为发动机气路颗粒物静电信号的有效表征提供模型基础。
(2)通过对静电传感器静态灵敏度分析表明,传感器长度和底面直径越大灵敏度越大,但是在传感器底面直径不变的前提下,随着传感器长度加长,沿传感器轴向,在距离传感器表面相同距离的整个周向的灵敏度分布逐渐平稳,不再发生明显变化。因此传感器的最佳长度可以在灵敏度达到平衡的时候得到,其最优长度大于8cm,这为传感器结构优化设计提供了理论基础。
(3)通过对静电传感器动态灵敏度分析表明,经过传感器的颗粒物的电荷量越多,感应电荷越大,颗粒速度越快,感应电荷变化率越大,频带越窄;综合速度和电荷大小两个因素对感应电荷信号的影响,进而可以实现对颗粒物直径的判别,最终为达到航空发动机气路颗粒物判别以及部件故障分析提供依据。
参考文献
[1]Yan Y,Byrne B. Measurement of solids deposition in pneumatic conveying[J]. Powder Technology,1997,91:131-139.
[2]Powrie H E G,Fisher C E. Engine health monitoring:Towards total prognostics[C]//Aerospace Conference,1999.
[3]Powrie H,Novis A. Gas path debris monitoring for F-35 joint strike fighter propulsion system PHM[C]// Aerospace Conference,2006.
[4]Novis A,Powrie H. PHM sensor implementation in the real world,a status report[C]//Aerospace Conference,2006.
[5]胡宇,李魁,张寅,等.基于快速原型的涡扇发动机气路部件在线健康监控系统设计[J].航空科学技术,2019,30(5):51-58. Hu Yu, Li Kui, Zhang Yin, et al. Research on online health monitoring system for gas path components of turbofan engine based on rapid prototyping [J]. Aeronautical Science & Technology, 2019, 30(5):51-58.(in Chinese)
[6]胡宇,石陸友,孙振生,等.基于奇异值分解的涡扇发动机线性状态模型能观度分析[J].航空科学技术,2018,29(2):73-78. Hu Yu, Shi Luyou, Sun Zhensheng, et al. Observable degree analysis about linear state model of turbofan engine based on the singular value decomposition [J]. Aeronautical Science & Technology, 2018, 29(2):73-78.(in Chinese)
[7]唐欣,胡政,陈仲生,等.探针式静电传感器灵敏度仿真分析与优化设计[C]//第15届中国科协年会第13分会场:航空发动机设计、制造与应用技术研讨会,2013. Tang Xin, Hu Zheng, Chen Zhongsheng, et al. Simulationbased sensitivity analysis and optimization of probe-type electrostatic sensor[C]// The 13th Session of the 15th Annual Conference of China Association for Science and Technology: Proceedings of the Symposium on Aero Engine Design, Manufacturing andApplication Technology, 2013.(in Chinese)
[8]冯阳博,高鹤明,华灯鑫,等.立体网状静电传感器空间灵敏特性研究[J].仪器仪表学报, 2015, 36(9):1953-1960. Feng Yangbo, Gao Heming, Hua Dengxin, et al. Sensitivity distribution of electrodynamic sensor array [J]. Proceedings of the CSEE, 2015, 36(9):1953-1960. (in Chinese)
[9]许传龙,汤光华,杨道业,等.静电传感器灵敏场有限元仿真研究[J].仪器仪表学报, 2007(7):161-168. Xu Chuanlong, Tang Guanghua, Yang Daoye, et al. Finite element analysis of the sensing field of electrodynamic sensor[J]. Chinese Journal of Scientific Instrument, 2007(7):161-168.(in Chinese)
[10]高鹤明,许传龙,王式民.阵列式静电传感器灵敏场分布特性[J].中国电机工程学报, 2010, 30(5):76-82. Gao Heming, Xu Chuanlong, Wang Shimin, et al. Sensitivity distribution of electrodynamic sensor array[J]. Proceedings of the CSEE, 2010,30(5):76-82. (in Chinese)
[11]刘尚合,杜照恒,胡小锋,等.航空发动机尾气静电带电机理分析与试验研究[J].高电压技术, 2014, 40(9):2678-2684. Liu Shanghe, Du Zhaoheng, Hu Xiaofeng, et al. Mechanism analysis and experimental research of aero-engine exhaust electrostatic charging[J]. High Voltage Engineering, 2014, 40(9):2678-2684. (in Chinese)
[12]GajewskiJB.Mathematicalmodelofnon-contact measurementsofchargeswhilemoving[J].Journalof Electrostatics,1984,15(1):81-92.
[13]Yan Y,Byrne B,Woodhead S,et al. Velocity measurement of pneumatically conveyed solids using electrodynamic sensors[J]. Measurement Science & Technology,1995,6(5):515-537.
[14]Murnane S N,Barnes R N,Woodhead S R,et al. Electrostatic modelling and measurement of airborne particle concentration[J]. IEEE Transactions on Instrumentation and Measurement,1996,45(2):488-492.
[15]殷逸冰,左洪福,冒慧杰,等.航空发动机进气道静电传感器空间模型解析及感应信号影响因素试验分析[J].仪器仪表学报, 2015, 36(4):795-803. Yin Yibing, Zuo Hongfu, Mao Huijie, et al. Spatial alysis of inlet electrostatic sensor and experimental study on influence factors of charge-induced signal[J]. Chinese Journal of Scientific Instrument, 2015, 36(4):795-803. (in Chinese)
[16]黄文杰,左洪福.滑油系统全流量磨粒在线监测静电传感技术研究[J].航空学报, 2013, 34(8):1786-1794. Huang Wenjie, Zuo Hongfu. Research on electrostatic sensing for in-line abrasive monitoring in full flow oil system[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8):1786-1794. (in Chinese)
[17]文振华.基于静电感应的航空发动机气路监测技术研究[D].南京:南京航空航天大学, 2009. Wen Zhenhua. Aero-engine gas path monitoring technology based on electrostatic induction[D]. Nanjing:Nanjing University ofAeronautics andAstronautics, 2009. (in Chinese)
[18]闞哲.基于静电传感器气/固两相流参数测量方法的研究[D].沈阳:东北大学, 2010. Kan Zhe. Study on measurement method of gas-solid two phase flow parameters with electrostatic sensors [D]. Shengyang: Northeastern University, 2010. (in Chinese)
[19]殷逸冰.面向气路部件健康管理的静电监测技术研究[D].南京:南京航空航天大学,2018.Yin Yibing. Research on electrostatic monitoring technology for gas-path component health management[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2018. (in Chinese)
(责任编辑陈东晓)
作者简介
张寅(1996-)男,硕士研究生。主要研究方向:航空发动机故障诊断。
Tel:13572191884
E-mail:944739046@qq.com
胡宇(1984-)男,博士,副教授。主要研究方向:航空发动机故障诊断。
Tel:15289360632
E-mail:huyu1222@163.com
Sensitivity Analysis of Electrostatic Sensor in Gas Path Based on Hybrid Mathematical Model
Zhang Yin,Hu Yu*,Sun Zhensheng,Zhang Hao,Zhou Wei
Rocket Force University of Engineering,Xian 710025,China
Abstract: The accurate characterization of the static signal and variation law of particulate matter in aeroengine is the theoretical basis for the design and monitoring of the static signal in aeroengine. Aiming at the problem that the simplified mathematical model of electrostatic induction is not reasonable and the model accuracy is not high, this paper starts from the analysis of the structure of bar electrostatic sensor, on the basis of deducing the side and bottom surface induced charge mathematical models, the static and dynamic sensitivity of the static sensor is analyzed by using the static induction hybrid mathematical model. The results show that the induced charge is related to the charge quantity, space position and motion characteristics of the electrostatic particles. The longer the length of the sensor, the stronger the static sensitivity in the projection center of the bottom surface of the sensor, and almost the same in the projection surface of the bottom surface. Static sensitivity increases gradually from the top to the bottom along the sensor axis equidistant from the side, then tends to be stable, and finally decreases. The larger the diameter of the bottom surface of the sensor, the greater the static sensitivity through the projection center of the bottom surface of the sensor. Under the premise of the same charge, particles with different velocities produce the same induced charge amplitude, and the faster the velocity, the narrower the output signal band. The particle with fast velocity has more induced charge, and the amplitude of induced charge rate increases with the increase of particle velocity. This will provide a theoretical basis for the structural optimization design and component fault diagnosis of aeroengine electrostatic sensor.
Key Words: aeroengine; electrostatic sensor; mathematical model; electrostatic induction; sensitivity

