计及综合因素的光伏接入配电网优选研究
许鸣吉,沈磊,李胜,郭健,刘嘉宝
(1.国网上海市电力公司市北供电公司,上海 200072;2.南京理工大学自动化学院,江苏 南京210094)
0 引言
在打造能源互联网和电力行业转型升级的背景下,分布式电源在电力系统中的比重快速增加[1]。光伏作为一种应用广泛的分布式电源,一般接入10 kV及以下电压的配电网[2]。光伏的接入改变了配电网的结构[3],突破了传统电源向配电网单相供电的格局,改变了系统潮流,这不可避免地会对配电网的电压质量、经济指标和安全性能产生影响[4—8]。目前,对光伏接入配电网的规划设计主要分为2个领域:在现有的配电网中对光伏的接入进行选址定容[9];综合协调已接入光伏的配电网,进行网络重构[10]。
早期对光伏选址定容问题的研究,以系统的单一指标为优化目标。文献[11]优选了配电网中分布式发电单元位置,研究了网损最小的分布式电源最优接入位置;文献[12]得到了光伏满足电压偏差范围的准入容量,提出了保证电压偏差要求的具体措施;文献[13]运用时域仿真法,考察了光伏电站接入配电网电缆线路引发故障对母线暂态电压稳定性的影响。上述文献未同时兼顾考察系统的电压质量、经济指标和安全性能,难以满足电网发展的需求。
文献[14]考虑了光伏对系统电压和网损的影响,以某时刻为基准,计算光伏准入容量和位置。目前,大量文献均选取某时刻的负荷数据,未考虑配电网潮流的动态变化,缺乏对各时刻负荷变化的联系与比较。此外,大量文献均以IEEE 33节点系统为算例进行分析,该方法不能满足我国配电网的实际要求,缺乏实用性。
有鉴于此,文中首先基于国网上海市北供电公司所辖35 kV德都站10 kV馈线德31德都北的配电网系统,从配电网的电压质量、经济指标和安全性能角度出发,推导光伏在不同接入位置、不同接入容量、密集和分散接入时对台区电压、线路损耗和电压稳定性的影响。其次,依据建立的光伏接入的优选模型,提出一种基于交互式决策数学模型的多目标优化方法。最后,依据德31德都北馈线的分析结果,研究接入光伏对配电网关键指标的影响,并求解出光伏接入的最优位置和最优容量方案。
1 光伏接入对配电网关键指标的影响分析
1.1 光伏出力模型
并网运行光伏发电系统可以将太阳能电池阵列输出的直流电转化为与电网同压、同幅、同频、同相的交流电,实现与电网连接,同时向电网输送电能[15]。
光伏出力与地区光照强度相关,光伏输出功率P可表示为[16]:
P=hSη
(1)
式中:h为某时段的光照强度;S为光伏电池板总面积;η为光电转化效率。光照强度h可近似看成服从Beta分布,可表示为:
(2)
式中:hmax为某时段的最大光照强度;α,β分别为该时段Beta分布的时间参数;Γ为Gamma函数。
1.2 光伏接入对配电网电压质量的影响
光伏接入会使馈线上各台区电压发生改变,对配电网电压质量产生影响[17]。接入光伏的馈线简化模型如图1所示。图1中定义变电站母线电压为U0,馈线上共有N个台区,第n个台区的电压为Un;负荷为Pn+jQn;线路的单位阻抗为r+jx;第n-1个与第n个台区间的线路长度为ln-1,n;位于台区i处的光伏注入功率为PPVi。

图1 接入光伏的馈线简化模型Fig.1 Simplified model of feeder connected to PV
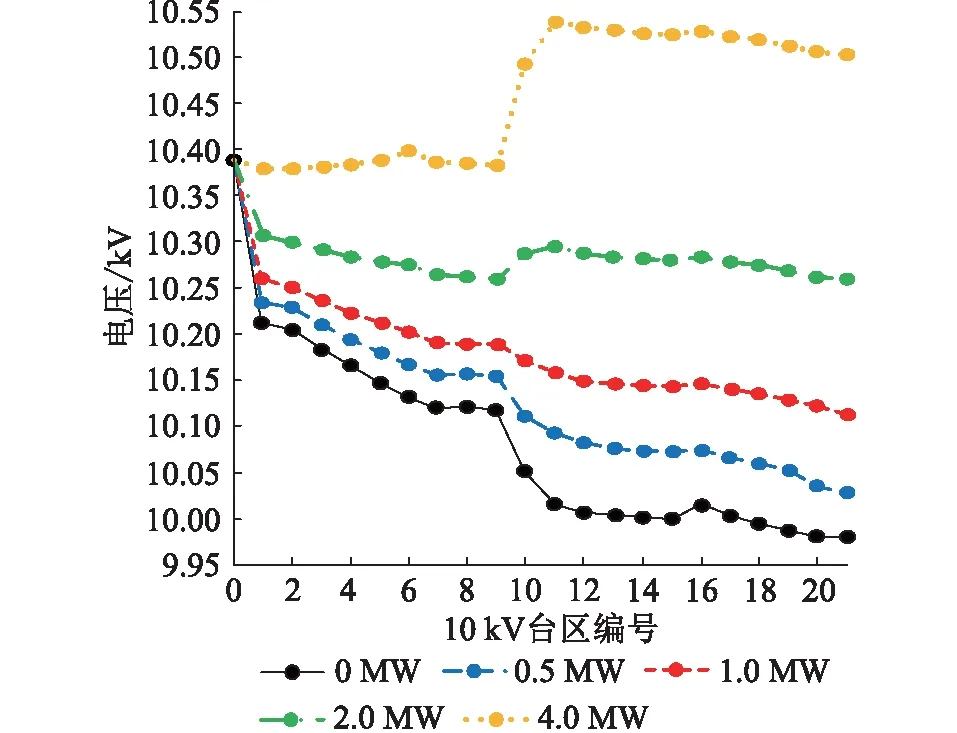
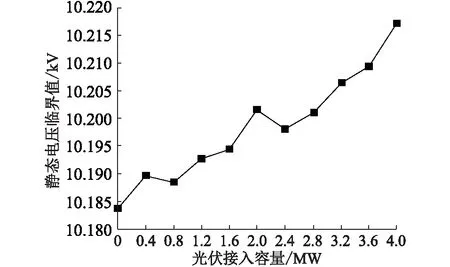
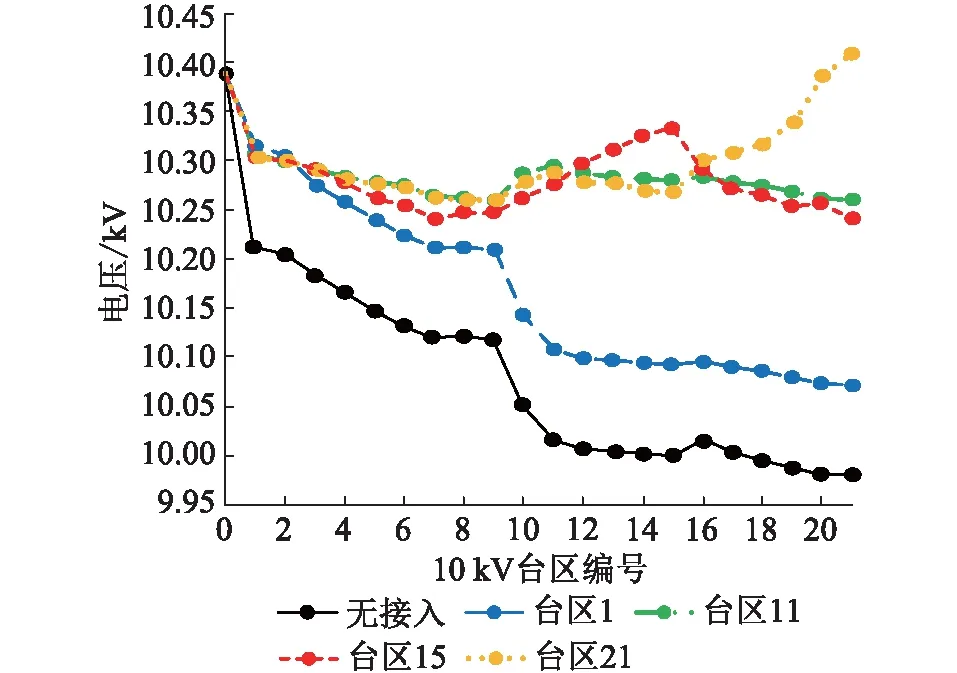
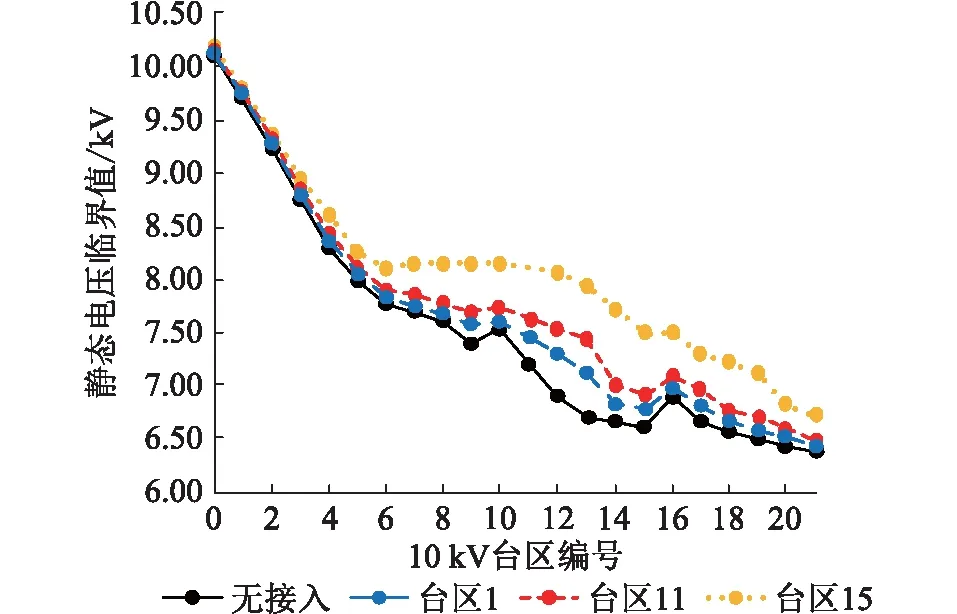
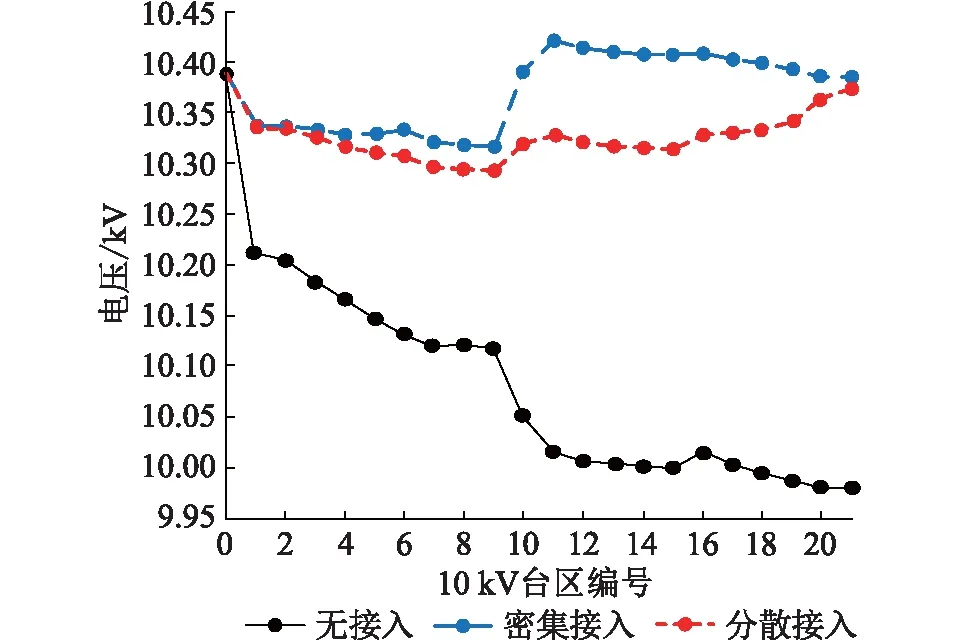
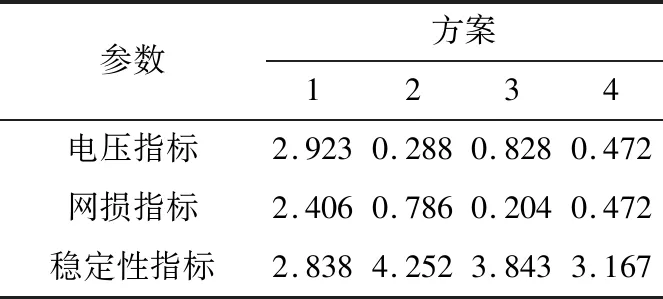
当台区n在光伏接入点i之前(0 (3) 由式(3)可知,当注入馈线的光伏功率PPV比第n个台区及之后的台区负荷Pk总和大时,第n-1个台区到第n个台区的压降ΔUn-1,n为负,第n个台区电压升高。否则,台区电压降低。 当台区n在光伏接入点i之后(i (4) 由式(4)可知,第n个台区的电压不变,始终比第n-1个台区的电压低。 配电网的线路损耗是衡量系统经济性的最重要指标。当台区n在光伏接入点i之前(0 (5) 由式(5)可知,当注入馈线的光伏功率PPV等于第n个台区及之后的台区负荷Pk总和时,线损ΔSn-1,n最小。 当台区n在光伏接入点i之后(i (6) 由式(6)可知,线损大小没有变化。 配电网作为电网的末端,无需像主网一样考虑频率稳定、静态稳定、动态稳定和暂态稳定。从安全性能考虑,光伏接入会改变配电网的静态电压临界值,对系统的电压稳定性产生一定影响。 (7) (8) 联立式(7)和式(8),按实部和虚部展开得: (9) Pjxlij-Qjrlij=UiUjsin(δi-δj) (10) 联立式(9)和式(10),消去(δi-δj)项得: (11) 上述方程有实数解的条件为: (12) 因此,可得支路的电压稳定性指标Us为: (13) 由式(13)可知,若配电网运行稳定,则Us<1;Us越小,表明系统的静态电压稳定性越高。 将光伏接入的位置容量优选问题转化为多目标优化问题,选择台区电压、线路损耗和电压稳定性作为目标函数。 (1) 台区电压目标表示各台区电压与母线电压的偏差程度,可表示为: (14) (2) 线损目标为馈线总线损与各台区负荷总和之比,即线损率,可表示为: (15) (3) 电压稳定性目标选取各支路中电压稳定性指标的最大值,可表示为: f3=maxUs(τ)=max[Us,1(τ),Us,2(τ),…,Us,n(τ)] (16) (1) 台区注入功率平衡的约束[15]: (17) 式中:Pp,i(τ)为台区i在τ时刻的有功功率;fij为潮流方向矩阵中的元素;PPV,i(τ)为光伏在台区i在τ时刻的出力;PL,i(τ)为台区i的有功负荷。 (2) 台区电压的约束: Ui,min≤Ui(τ)≤Ui,max (18) 式中:Ui,max,Ui,min分别为台区i电压幅值的上下限。 (3) 支路最大电流的约束: Iij(τ)≤Iij,max (19) 式中:Iij,max为支路ij允许流过的最大电流。 (4) 变压器最大容量的约束: Sk(τ)≤Sk,max (20) 式中:Sk(τ),Sk,max分别为变电站中变压器k在τ时刻的功率值和最大容量。 (5) 光伏出力的约束: PPV,i,min≤PPV,i(τ)≤PPV,i,max (21) 式中:PPV,i,max,PPV,i,min分别为光伏i出力的上下限。 为优化各个目标使其同时达到综合的最优值,引入多目标交互式决策数学模型[18],可表示为: max[f1(X),f2(X),f3(X)] s.t.X∈S (22) 式中:f1(X),f2(X),f3(X)分别为台区电压单目标、线路损耗单目标和电压稳定性单目标;S为X的约束集。将光伏接入的优选问题中,决策变量代表每一个台区接入的光伏容量。 对3个单目标的最优解f1,min,f2,min,f3,min进行归一化处理,得到单目标满意度函数ξ1(X),ξ2(X),ξ3(X),可表示为: (23) 式中:f1,max,f2,max,f3,max分别为未接入光伏前馈线的台区电压目标、线路损耗目标和电压稳定性目标。 为在约束集S内求得决策向量解X*,使ξ(X)最逼近ξ*(X)。定义整体均衡度决策函数f为: (24) 式(24)中一定程度上存在如下关系:l(x)越小,ξi(X)越大,fi(x)越小。即各个目标函数越逼近各自的最佳目标值。所以,l(X)能够充分实现多个目标函数的整体均衡,既尽最大可能实现了各自的利益最大化,又同时兼顾了各方的矛盾,成为各方均能接受的满意方案。 粒子群算法具体求解步骤如下。 步骤一:随机初始化光伏的容量与位置; 步骤二:对初始化种群进行潮流计算,计算得到各节点的电压值; 步骤三:对种群中每个粒子的适应值进行计算,并更新局部最优值与全局最优值; 步骤四:判断迭代次数是否满足最大迭代次数,若满足则输出结果,若不满足则转到步骤五; 步骤五:采用云模型模糊控制规则对学习因子和惯性权重进行调节; 步骤六:更新种群中光伏的位置与容量; 步骤七:判断每个粒子的光伏容量是否越限,若不越限则转到步骤二,若越限则将越限的容量更新为容量的边界值后转到步骤二。 文中选取国网上海市北供电公司所辖月浦地区35 kV德都站10 kV馈线德31德都北进行分析,该馈线所送21个台区(包括18个杆变、3个配电站)以居民负荷为主,负荷密度大。将德31的馈线模型简化,如图2所示,简化模型中标识了各台区编号和支路阻抗,阻抗单位为Ω/km。 图2 德31德都北馈线的简化模型Fig.2 Simplified feeder model of De 31 Dedubei 各台区负荷由配电负荷检测系统TsRun实时监测。德31馈线的线路阻抗为0.125+j0.08 Ω/km;2019年负荷最高日7月30日12:45时刻总负荷为3 275.20 kW+j605.10 kvar,母线电压为10.39 kV。 3.2.1 光伏接入容量的变动对指标的影响 在台区11处分别接入0.5 MW,1.0 MW,1.5 MW,2.0 MW,4.0 MW光伏,并网运行功率因素为0.95,各台区的电压变化如图3所示。在未接入光伏前,各台区电压沿馈线辐射方向逐渐下降。光伏的接入改变了系统的潮流方向,提升了各台区电压。随着光伏容量的增加,对各台区电压的支撑作用明显增强,光伏接入点之前的台区电压先依次降低后升高,之后的台区电压依次降低,光伏接入点所在的台区局部电压最高。当光伏容量过高时,该台区电压可能会越过电压上限。 图3 台区11接入不同容量光伏时的电压分布曲线Fig.3 Voltage distribution curve of area 11 in different photovoltaic capacity 随着台区11接入的光伏容量不断增加,系统网损的变化如图4所示。网损呈现先减少后增加的趋势,验证了光伏接入容量不是越大越好,当注入馈线的光伏功率PPV等于第n个台区及之后的台区负荷Pk总和时,网损ΔSn-1,n最小。 图4 台区11接入不同容量光伏时的系统网损曲线Fig.4 Network loss distribution curve of area 11 in different photovoltaic capacity 在台区11接入不同容量光伏时的静态电压临界值曲线如图5所示,系统静态电压临界值随着光伏接入容量的增加而变大,这说明当系统中负荷骤增时,光伏接入容量越大,系统的电压稳定性越差。 图5 台区11接入不同容量光伏时的静态电压临界曲线Fig.5 Static voltage critical curve of area 11 in different photovoltaic capacity 3.2.2 光伏接入位置的变动对指标的影响 分别在台区1、台区11、台区15和台区21处接入2 MW光伏,各台区电压分布如图6所示。光伏接入的位置不同,各台区电压大小分布不同。光伏接入处越靠近馈线末端,对电压的提升作用越明显,但可能会导致在馈线终端的台区电压越过上限。所以光伏适宜接入馈线中间偏终端的台区。 图6 不同台区接入2 MW光伏时的电压分布曲线Fig.6 Voltage distribution curve when 2 MW photovoltaic is connected to different stations 分别在不同台区接入2 MW光伏,系统的网损曲线如图7所示。接入适度光伏能减少系统网损,在台区11和台区16处接入光伏时,系统网损明显能降到最低的范畴,这表明光伏适宜接入馈线中间偏终端的台区。 图7 不同台区接入2 MW光伏时的系统网损曲线Fig.7 Network lossdistribution curve when 2 MW photovoltaic is connected to different stations 分别在台区1、台区11和台区15处接入2 MW光伏,各台区的静态电压临界值分布如图8所示。随着光伏的接入位置越靠近馈线末端,系统的静态电压临界值明显增大,这说明当系统中负荷发生突变时,光伏接入位置越靠近终端,系统的电压稳定性越差。 图8 台区位置对系统静态电压临界值的影响曲线Fig.8 Static voltage critical curve when photovoltaic is connected to different stations 3.2.3 光伏的密集和分散接入对指标的影响 在台区11处集中接入3 MW光伏、分别在在台区1、台区11和台区21分散接入1 MW光伏,系统的电压分布曲线如图9所示。 图9 密集接入和分散接入时的电压分布曲线Fig.9 Voltage distribution curve of dense access and decentralized access 由图9可知: (1) 密集接入引起接入台区的电压骤升或骤降,分散接入能均衡提升各台区电压。 (2) 密集接入时,系统网损为22.95 kW;分散接入时,系统网损为11.57 kW。较密集接入,各台区分散接入光伏能有效降低系统网损。 (3) 密集接入时,光伏接入容量越大,系统的静态电压临界值越大,系统的电压稳定性越差。分散接入时,接入点越多越能分散对系统静态稳定性的影响。 对光伏接入的优选问题进行分析,受地理位置城市规划和建设与管理成本等因素影响,发展部门设置最多可接入3处光伏,可接入台区编号为1至21,可接入的容量不大于2 MW且均为0.1 MW的整数倍。对2019-07-30的07:00—19:00德31德都北馈线进行分析,配电负荷检测系统每15 min采集一次数据,共获得48组数据。考虑到电压、网损和稳定性指标同等重要,ξ1(X),ξ2(X),ξ3(X)均取1。如图10所示,各时刻平均的整体均衡度在迭代43次时收敛于0.182。 图10 迭代曲线Fig.10 Iterative curve 各优选方案的接入位置及光伏接入容量如表1所示。优选后各方案的指标对比如表2所示,方案2以电压为单目标,电压指标较未接入光伏时下降至0.288%,为最优解;方案3以网损为单目标,网损指标下降至0.204%,为最优解;方案4以多目标进行优选时,得到了最优的整体均衡度,各项结果虽然不是最优,但可以使电压和网损指标同时得到改善,且稳定性指标没有大幅度上升。该优选方案验证了所提方法的可行性和有效性。 表1 德31德都北光伏位置容量的优选方案Table 1 Optimal schemes of photovoltaic locationand capacity in line De 31 Dedubei 表2 4种优选方案的评价参数Table 2 Evaluation parameters for four optimal schemes % 文中提出计及综合因素的光伏接入配电网优选方案。将台区电压、线路损耗和电压稳定性作为决策子目标,利用基于交互式决策数学模型的多目标优化方法对配电网光伏安装位置和容量进行选择。研究发现光伏接入配电网会对系统的电压质量、经济指标和安全性能产生影响。据此,文中建立了光伏接入的优选模型,提出了一种基于交互式决策数学模型的多目标优化方法。 通过对上海市北电网德31德都北馈线进行分析,研究了接入光伏对配电网关键指标的影响,并求解出光伏接入的最优选方案,为光伏发电项目的规划设计提供了理论依据。后续将以35 kV光伏电站为目标,研究其对系统的影响。
1.3 光伏接入对配电网经济指标的影响
1.4 光伏接入对配电网安全性能的影响
2 光伏优选的多目标交互式模型
2.1 目标函数

2.2 约束条件
2.3 多目标交互式决策数学模型
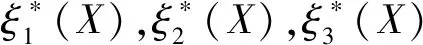
2.4 粒子群算法求解流程
3 德31德都北案例分析
3.1 案例描述

3.2 接入光伏对关键指标的影响分析


3.3 对光伏接入优选问题的分析


4 结语

