新能源全消纳并网友好型虚拟发电厂优化调度研究

徐天奇，田业，高鑫，李红坤，李琰

(1.云南民族大学电气信息工程学院,云南 昆明 650500；2.江西洪都航空工业集团有限责任公司，江西 南昌330001)

0 引言

新能源发电是有效解决气候变暖等问题的方法之一[1]，但其不可控性和随机性十分突出[2]，因此当新能源大规模并网时，会严重妨碍电网的稳定、经济运行[3—4]。新能源发电的快速发展，已经给传统电力系统造成巨大压力[5—6]，弃风弃光现象比较严重。

分布式新能源发电投资小、灵活方便，近年来得到快速发展。虽然分布式新能源发电单机容量小，但当其大规模并网时，由于规模效应和气候条件时空相关性，出力不确定性可能会被放大，从而给电力系统频率稳定和可靠性带来严重挑战，反而可能会限制分布式新能源的发展[7—8]。

虚拟发电厂(virtual power plant，VPP)技术是解决这个问题的可行性方案之一。VPP通过分布式控制、精确计量和实时通信等技术，把分布在不同地域的不同类型分布式电源、储能系统、可控负荷、传统负荷等元件在逻辑上聚合在一起，通过实时调度软件实现整体的协调和优化运行，使其从电网角度看来与一个传统电厂类似[9—11]。作为一种新的运营管理模式，VPP在整合分布式新能源方面显现出巨大的潜力。利用VPP的协调控制优化，可以显著降低分布式电源因分别单独并网对电力系统造成的不利影响。通过分布式电源有序接入电网，增加整个系统运行的可靠性，在充分利用新能源出力的同时，可显著改善电网出力不稳定的情况，既能保证电力供应安全、优质、经济、环保的基本需求，也能满足充分消纳可再生资源的要求[12—13]。另外，利用VPP技术，不需要对电网进行改造，也不会改变各个分布式电源与电网连接的方式。

文献[14]把建筑当做VPP来管理，利用可延迟负荷作为资源进行调度，实际上只是需求侧响应而并不是真正的VPP；文献[15]将新能源分布式发电、水电站、抽水蓄能以及当地负荷组成VPP，以主网交换电量最低及电费最低为目标进行调度；文献[16]提出由风电、可再生能源发电技术(power to gas，P2G)、燃气机组炭捕集以及热点联产燃气机组聚合为VPP,以VPP受益最大为目标进行调度；文献[17]从电力市场的角度考虑VPP的调度问题，同时对日前市场和实时市场交易进行优化，引入条件风险价值系数来衡量日前市场和风光出力预测的不确定性，仅把风险作为一个可选择的参数并入利润，未能体现不确定性对调度的影响。这些研究都未将新能源消纳作为调度目标之一，也未考虑VPP并网功率的平稳性。

为了尽可能地消纳新能源，并使VPP更加平稳地向电网输送电能，文中提出波动因子及奖惩机制，以可中断负荷和储能系统为调度资源，构建新能源全消纳的VPP并网经济效益最大化模型，通过粒子群算法[18]进行寻优，得到VPP的利润最优值。算例对比验证了此调度模型可使VPP获得最大经济效益，同时提高并网功率的平稳性。

1 VPP模型

文中考虑以一个包含分布式风力发电、光伏发电、储能系统、普通负荷和可中断负荷的VPP向电网供电，如图1所示。

图1 含分布式新能源的VPPFig.1 VPP containing distributed new energy power generation

以促进分布式新能源发电并网规模化应用为目标，考虑的VPP内部的发电单元仅包含分布式新能源而不包含传统分布式电源。

针对图1所示含分布式新能源的VPP，以储能系统和可中断负荷作为调度资源，对新能源进行全部消纳，可中断负荷良好的可调节性[19]以及储能系统的转移特性[20—21]一定程度上可以弥补新能源发电出力随机性给电网带来的负面影响。

2 VPP成本模型及奖惩机制

2.1 电池储能系统成本模型

文献[22—23]提出考虑寿命损耗成本的储能单元分布式协同控制策略，但该成本模型只考虑了电池储能系统的寿命成本。在此基础上，文中提出一个更加完整的电池储能系统成本模型，不仅考虑电池储能系统的寿命成本，还包括了电池储能系统的运维的成本和能量损失成本，如下所示：

CB=∑(Cbl+CO&M+Cpl)

(1)

其中：

(2)

(3)

(4)

2.2 可中断负荷的成本模型

可中断负荷的成本包括可中断容量成本和中断电量成本[24—25]，即：

(5)

其中：

(6)

CILk,t=∑(CILk0,tQILk,t)

(7)

2.3 波动因子

分布式新能源自身的不可控性会严重影响新能源发电并网的稳定性，为了有效保证VPP能安全稳定地向电网输送电能，引入波动因子参数来衡量VPP输出稳定性。文中使用VPP出力的标准差来定义波动因子参数，标准差是反映一组数据离散程度最常用的一种量化形式，是衡量精确度的重要指标。从定义上看，如果波动因子参数的数据离散程度越高，稳定性越差；反之，稳定性越好。波动因子参数的表达式为：

(8)

式中：σ为波动因子参数；Pt为t时刻VPP向电网输送的有功功率；μ为T时间段内VPP向电网输送的有功功率的平均值。

2.4 基于波动因子的奖惩机制

为了保证波动因子参数σ的有效性，引入基于波动因子的奖惩机制。当波动因子参数控制在某一个较小数值的区间范围内时，说明VPP向电网输送电能的稳定性较好，VPP将会得到一定来自电网的奖励；反之，当波动因子参数在一个较大数值的区间范围波动时，说明VPP向电网输送电能的稳定性较差，VPP将会受到一定的惩罚。波动因子奖惩值表示为：

(9)

式中：σ0为VPP未协调控制前分布式新能源向电网输送电能的初始标准差。

3 考虑新能源消纳的VPP优化调度模型

3.1 目标函数

以储能装置的充/放电功率和可中断负荷作为有效调控资源，考虑电池储能系统损耗成本及可中断负荷成本，通过最大化消纳可再生能源资源来实现VPP的最优经济效益。目标函数为：

(10)

其中：

(11)

(12)

式中：R为VPP整体的净利润；T为新能源消纳的时间段，取24 h；Pt为VPP向电网输送的电能；Nw为风力发电厂的个数；Np为光伏发电站的个数；Pwi,t为风电场i在t时段的有功出力；Ppj,t为光伏发电站j在t时段的有功出力；λD,t为t时段的日前电价；λL,t为t时段的内部负荷供电电价；PL,t为t时段的内部负荷的消耗量；PIL,t为t时段的可中断负荷调用值；CB为电池储能系统的总损耗成本；C(PIL,t)为可中断负荷在t时段的调用成本；NIL为可中断负荷组数；CILck,t为可中断负荷用户k在t时段的电价折扣；QILck,t为可中断负荷用户k在t时段的可中断容量；CILk0,t为可中断负荷用户k在t时段单位削减成本；QILk,t为用户k的t时段负荷削减量。

3.2 约束条件

(1) 可中断负荷调用约束条件。

(13)

式中：PIL,min,t，PIL,max,t分别为t时段可中断负荷的调用容量上、下限；SILk,t为可中断负荷k在t时段的调用状态，为0表示可中断负荷k在t时段没有被调用，为1表示可中断负荷k在t时段被调用；PILk为可中断负荷k的调用容量。

(2) 电池储能系统的约束条件。

gbmin≤gb,t≤gbmax∀b∈B

(14)

ub,t+vb,t≤1

(15)

(16)

(17)

(18)

4 算例分析

4.1 算例介绍

建立一个VPP，其中包括1个风电场，1个光伏电站，负荷(含可中断负荷)和储能4种分布式组成单元。VPP中的风力出力曲线如图2所示，光伏出力曲线如图3所示，内部负荷曲线如图4所示。

图2 VPP风力出力曲线Fig.2 Wind power output curve of VPP

图3 VPP光伏出力曲线Fig.3 Photovoltaic power output curve of VPP

图4 VPP内部负荷曲线Fig.4 Internal load curve of VPP

VPP内部负荷供电电价和VPP卖给电网的电能都采用固定电价，如购电价格490元/(MW·h)，售电价格380元/(MW·h)，可中断负荷的参数信息如表1所示。在储能系统中，电池储能系统容量为300 MW·h，初始状态时电池深度为0，建设成本为4 500元/(MW·h)，充电效率为0.87，寿命成本参数a=1 534，b=2.4，运维成本为59元/(MW·h)，能量损失为25.3元/(MW·h)，储能电池剩余电量的上、下限分别为300 MW·h和0。

表1 可中断负荷参数信息Table 1 Parameter information of interruptible load

4.2 优化结果及分析

根据文中所提出的模型，采用粒子群算法对其求解，以验证文中所提模型的可行性和波动因子有效性。其中，粒子群算法参数设置为：种群规模为100，最大迭代次数为300，惯性权重因子w为0.7，学习因子C1，C2均为2.05。寻优结果如图5所示，可以看出，大约迭代80次左右收敛，最终得到的总收益利润最大为1 745 834元。

图5 总收益进化过程Fig.5 Evolution of total revenue

当VPP利润最优时，可中断负荷和储能系统一天内各个时刻的调用情况如图6所示，图中可中断负荷的取值代表本小时本中断的负荷功率，储能系统状态则代表充放电功率，正半轴为充电状态，负半轴为放电状态。调用中断负荷和储能系统放电，意味着新能源发电不足或内部总负荷增加，而储能系统充电则意味着新能源发电过剩，若全部输出到电网可能引起VPP输出功率波动过大。

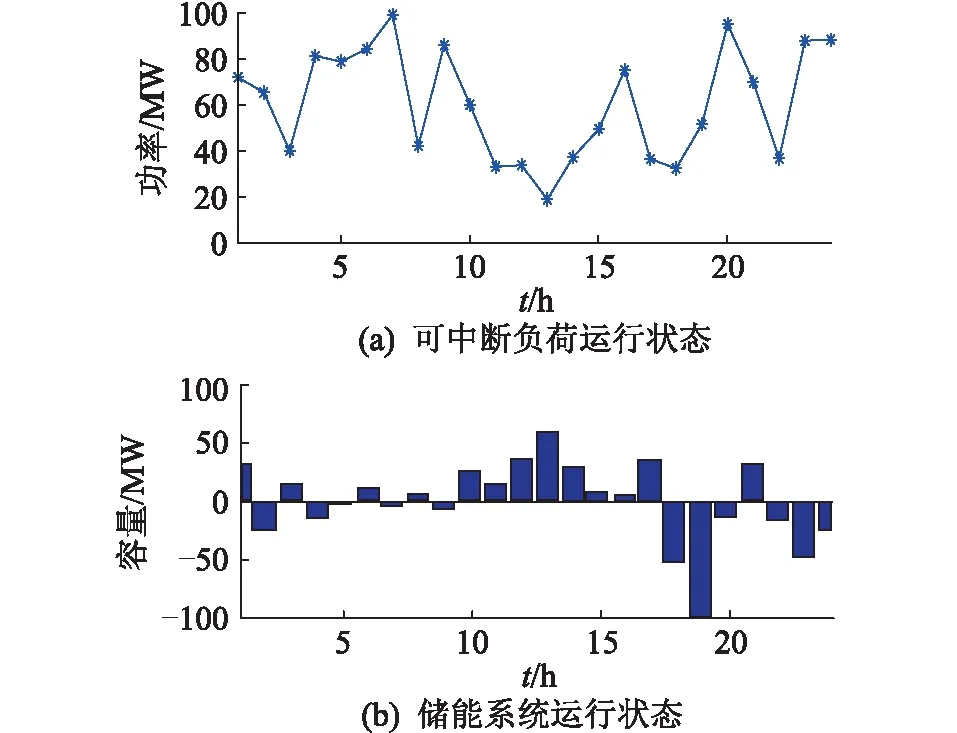
图6 可中断负荷和储能系统调度状态Fig.6 Dispatching states of interruptible load and energy storage system

图7为加入波动因子前和加入波动因子后VPP一天内各个时刻向电网输送功率的变化曲线。可以看出，加入波动因子后，出力变化曲线明显变得平缓，说明了引入波动因子的有效性。图7中引入波动因子前的曲线出现负值的原因是VPP具有“源荷”双重性，既可以作为电源向电网供电，又可以作为负荷向电网购买电能。

图7 VPP并网功率的变化曲线Fig.7 Variatio curve of grid-connected power of VPP

5 结论

文中构建了基于VPP的分布式能源消纳优化调度模型，此模型把储能系统和可中断负荷作为调度资源，在考虑储能系统和可中断负荷调度成本的基础上，引入波动因子参数并对其大小所属区间采取相应的奖惩机制来保证VPP出力稳定性，同时以VPP总体收益最大为目标进行优化。采用粒子群算法进行寻优，结果表明：(1) 电池储能系统成本模型不仅应考虑寿命成本，即安装成本，还应考虑运维成本和能量损失成本；(2) 引入波动因子来衡量输出稳定性，可以在一定程度上降低新能源出力的不确定性对电网造成的影响，并提高新能源消纳的水平；(3) 不可控新能源大规模入网时，通过可中断负荷和储能系统联合运行，可以弥补彼此的局限性和成本代价，使VPP获得良好的经济效益，提高电网的电能质量。