考虑风机排序的风电集群分层有功控制策略

程雪婷，张家瑞，刘新元，郭文博，郑惠萍，薄利明

(1.国网山西省电力公司电力科学研究院，山西 太原 030001；2.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林 吉林 132012；3.罗切斯特大学文理学院，美国 纽约州 罗切斯特 14627)

0 引言

我国风电多以集群方式接入电网，随着风电渗透率的提高，风电场弃风限电现象愈发严重[1—3]。结合功率预测信息对风电场群进行合理有功控制、减少风机调控次数以及提高风电消纳量已成为亟待解决的问题之一。

目前风电场单场的有功控制已取得一定成效。文献[4—6]提出了风电场分层预测控制策略，对风电场进行有功分层，并通过反馈提高预测精度。文献[7—8]对含双馈感应风机的风电场提出了场内分层控制策略，并建立了风电场-机组层有功调控模型。文献[9—10]对风机调控能力进行分析，在一个调度周期内对风电场的风机进行排序，按排序结果确定风机动作顺序。文献[11]提出了多Agent合作控制的风电场功率控制模型，减少了风电场的功率波动。上述研究多集中于风电场层的控制策略，且大多采用分层控制理念，在平抑风电功率波动、提高风电场调控能力上取得了一定进展。目前我国风电场多以集群形式存在，因此亟需研究风电集群控制策略，进一步提升系统风电消纳能力。

在风电场单场控制策略基础上，针对风电场群控制的研究也取得了一定进展。文献[12]针对大规模间歇式能源发电提出了包含集群、场群、场站、机组的多层控制框架。文献[13—16]通过对风电场群的分层控制，在降低系统网损的同时提高了调度精度。文献[17—22]将不同时间尺度的功率预测与不同空间上的风电场群相结合，提出多时空尺度风电集群有功分层控制策略，并与预测控制模型相结合，在满足调度计划的同时提高了风电消纳量。上述文献针对风电集群控制研究取得了一定成效，但仍缺乏针对风机组层调控指令合理下发、减少风机调控次数等方面的研究。

文中针对风电集群控制，提出分层优化控制理念，即根据区域的不同将风电集群划分为场群层、风电场层和机组层，并结合功率预测信息，在场群层、风电场层/机组层分别采用15 min和5 min时间尺度进行预测，实现多时空尺度风电分层有功控制。在机组层中对影响机组调控能力的因素进行分析，并使用熵值法以及隶属度函数对各机组在下一调度周期内的调控能力进行排序。根据上一层下发的调度指令并结合各机组的调控能力，制定机组的动作顺序以及出力计划。最终通过算例分析，验证所提模型在提高风电消纳能力、减少风机调控次数方面的可行性。

1 风电集群分层有功控制策略

由于风电场单场出力波动大，传统按单场分配出力的调度方式会造成出力分配不合理，不利于提高风电消纳能力和风机调控能力。文中结合超短期功率预测技术，将风电场按所在区域的不同划分为不同的场群，每一场群层又包含对应的风电场层，每一风电场又对应相应的机组层。在控制时实现场群-风电场-机组的逐级调控。需要指出的是，文中认为所采用的超短期功率预测技术可达到国家标准，且整个调度过程中风电场上报预测信息真实准确。多时空尺度风电集群分层有功控制方法如图1所示。

图1 多时空尺度风电集群分层有功控制Fig.1 Hierarchical active power control of multi-temporal-spatial scale wind power cluster

首先，调度中心向场群层下发风电集群有功调度指令。根据这一调度指令，场群层调控模型以时间尺度为15 min的风电预测为基础，优化各场群的有功调度指令，并下发至风电场层。该调度指令的时间尺度为15 min。

然后，风电场层接收到场群层的调度指令后，根据5 min时间尺度的风电预测，优化各风电场的有功调度指令，并下发至每一风电场的机组层。该调度指令的时间尺度为5 min。

最后，机组层根据所在风电场在调度周期中需完成的调度出力，进行排序控制，优化各风机的调控次序。机组层控制的时间尺度为5 min。各层控制的时间尺度参考文献[13]。

通过场群层-风电场层-机组层的逐级优化调控，降低了风电集群弃风量，减少了风机调控次数。

2 场群层调控模型

对于调度指令大于该时段各场群总预测出力的情况，场群处于“最大出力模式”，即该时段各场群的出力计划值均为预测所能达到的最大出力值。而调度指令小于各场群总预测出力时，风电场群处于弃风限电状态，此时各场群工作于“计划功率模式”，调度的目标为弃风量最小，调度的周期为15 min。

2.1 场群层目标函数

场群层目标函数如式(1)所示。目标函数可使场群层弃风量最小。

(1)

式中：T1为一天内场群层处于“计划功率模式”的调度时段总和；t为第t个调度周期，调度周期时长为15 min；n为场群层数目；Pcq,i,t为场群i在时段t的调度计划值；Ppre,cq,i,t为场群i在时段t的预测值。

2.2 场群层约束条件

(1) 场群出力应满足调度指令需求。

(2)

式中：Psys,t为第t个调度周期的调度指令值。

(2) 风电场群爬坡约束。

|Pcq,i,t+1-Pcq,i,t|≤Rdi

(3)

式中：Rdi为风电场群i的爬坡能力。

(3) 场群出力约束。

Pcq,i,t≤Pcq,i,t+1

(4)

(4) 场群传输容量限制。

Pcq,i,t≤Ptran,cq,i

(5)

式中：Ptran,cq,i为场群i的传输容量限制。

对于“最大出力模式”，场群的出力计划值为：

Pcq,i,t=Ppre,cq,i,t

(6)

通过计算得到场群层在每一调度时刻出力计划值，并将这一计划值以15 min为周期下发至风电场层。

3 风电场层调控模型

风电场层同样工作于“最大出力模式”与“计划功率模式”，其控制周期为5 min。风电场层的优化目标为弃风量最小，由于预测精度的差异，风电场应最大程度跟踪场群层发送的调度指令。对于“计划功率模式”下的风电场层有功控制模型，有如下目标函数和约束条件。

3.1 风电场层目标函数

(7)

式中：T2为1 d内风电场层处于“计划功率模式”下的调度时段总和;m为风电场层数目；Pfc,l,k为风电场l在时段k的调度计划值；Ppre,fc,l,k为风电场l在时段k的预测值；Pcq,t为风电场群在时段t的调度值；时段k的时间间隔为5 min。

3.2 风电场层约束条件

(1) 风电场层计划值不应超过场群层下发指令值。

(8)

(2) 各风电场爬坡约束。

|Pfc,l,k+1-Pfc,l,k|≤Rul

(9)

式中：Rul为风电场l的爬坡能力。

(3) 风电场出力约束。

Pfc,l,k≤Ppre,fc,l,k

(10)

(4) 风电场传输容量限制。

Pfc,l,k≤Ptran,fc,l

(11)

式中：Ptran,fc,l为场群l的传输容量限制。

对于“最大出力模式”，风电场的出力计划值为：

Pfc,l,k=Ppre,fc,l,k

(12)

通过场群层以及风电场层的上层控制模型优化得到风电机组的调度指令。

4 机组层排序控制建模

风电机组排序控制是按照各机组的调控能力由强到弱进行排序，流程如图2所示。首先，选出影响风机调控能力的评价指标；其次，确定各指标在最终机组调控能力综合评价值中的权重，并计算机组调控能力综合评价值；然后，对风电机组状态进行评定，划分出弱出力机组与可调机组；最后，结合机组调控能力评价值与风机状态，确定风机调控次序。

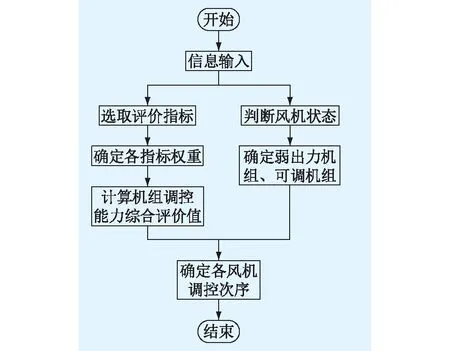
图2 风电机组排序控制流程Fig.2 Flow of wind turbine sequencing control

图3为风电机组实时有功控制框图，末端风机将机组排序所需数据上传至处理器，通过计算得到文中设定的反映风电机组调控能力的4个指标(见4.1节)，进而输入到风电机组有功控制层。该层对风机调控能力进行排序，得到各风机状态，最终获得各台风机调控指令，下发至功率控制器，控制风机出力值。

图3 风电机组实时有功控制Fig.3 Real-time active control of wind turbine

4.1 风电机组调控能力评价指标

风电机组调控能力主要受机组调节裕度大小、机组下一时刻上/下爬坡状态、风电机组的风电利用率、风电机组的调节速率等指标影响。

(13)

式中：Ph,k为第k个调度周期机组h的出力值；PN,h为机组h的额定容量。

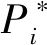
(2) 机组下一时刻爬坡状态a*。

a*=Ph,k-Ppre,h,k+1

(14)

式中：Ppre,h,k+1为下一时刻机组h的预测出力值。

若a*为正，则机组在下一调度周期内处于下爬坡状态，反之则为上爬坡状态。

(3) 机组的风电利用率η*。

(15)

式中：q为第1个调度周期到当前调度周期总的机组调度次数；η*为到当前调度周期风电机组总出力占额定值的百分比，η*越大，则机组运行状况越好。

(4) 风电机组调节速率v*。

(16)

v*越大，机组接到上层调度指令后完成的效率越高，执行度越大，风电机组调控能力越强。

4.2 基于熵值法的指标权重计算

指标权重是风电机组调控排序的重要依据，为了客观评价各指标对风电机组调控能力的影响，文中采用熵值法求解各指标权重，具体参考文献[9]。经过熵值法确定权重系数矩阵U，其中u1，u2，u3，u4分别对应4个评价指标。

U=[u1u2u3u4]

(17)

4.3 机组调控能力综合评价值计算

机组调控能力的综合评价值采用加权求和的方式计算。

(18)

式中：fhj为机组h第j项评价指标的评价集；Ah为机组h的综合评价指标，Ah越大，表示机组整体调控能力评价越高，排序越靠前。

相对于降功率场景，文中提出的评价指标为增益型指标，将指标j对应的评价分为“强”、“较强”、“中”、“差”4个层次。对应“强”的风电机组调控能力最好，而对应“差”的机组不考虑对其调控。假设4个层次的分界点分别为b1,b2,b3,b4,借用隶属度函数计算评价集fhj的值。

隶属度函数包括正态分布、梯形分布、岭形分布和抛物形分布4种，文中根据fhj特点选择半梯形分布作为隶属度函数进行计算。

(19)

(20)

(21)

(22)

式中：L1j(xhj)，L2j(xhj)，L3j(xhj)，L4j(xhj)分别对应“强”、“较强”、“中”、“差”4个层次；xhj为机组h的第j个评价指标。

通过隶属度函数可以求得各指标的隶属度值，赋予L1j(xhj)，L2j(xhj)，L3j(xhj)，L4j(xhj)权值分别为0.4，0.3，0.2，0.1，进而求得风电机组h在指标j下的评价集fhj为：

fhj=0.4L1j+0.3L2j+0.2L3j+0.1L4j

(23)

通过式(18)，求得各机组的调控能力综合评分Ah。

4.4 风机状态确定

风机可按目前调度时刻的出力情况分为弱出力机组和可调机组。其中弱出力机组满足：

Ph,k≤βPN,h

(24)

式中：β取0.1。

对于“降出力模式”的风电机组，弱出力机组只有采用停机才可实现出力下调。除弱出力机组外，其余机组都被划分为可调机组。

可调机组的下调限额为：

Pmin,j,h=αPN,h

(25)

式中：α取0.1；可调机组在降出力周期内最小可调至Pmin,j,h。

对各机组调控能力评分进行排序，并结合机组状态确定机组的最终调控次序。

5 算例分析

以山西电网实际风电场数据为例，分别在场群层、风电场层、机组层进行算例分析，并将文中所提控制方法与传统控制方法进行对比。风电场数据如表1所示。

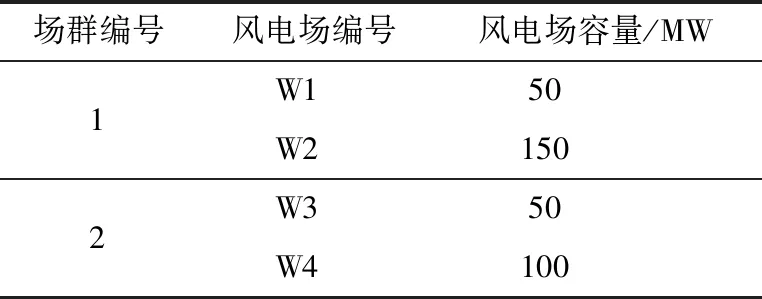
表1 风电场编号及其装机容量Table 1 Number and installed capacity of wind farm

传统固定比例控制方法的各风电场出力为：

(26)

式中：Pfc,l为风电场l的调度出力值；Pmax,fc,l为风电场l的最大出力值。

传统的固定比例控制方法是按风电场容量比例将下发的调度指令分配给各风电场以及风电机组。

传统变比例控制方法的各风电场出力为：

(27)

传统变比例控制方法按风电机组在下一调度周期的预测值进行有功功率分配。

5.1 场群层和风电场层算例分析

根据所在区域的不同将算例中的4个风电场划分为2个不同的场群，其中W1和W2风电场为场群1，W3和W4风电场为场群2。图4为通过文中分层控制方法得到的场群层及风电场层功率计划值。在调度值高于风电预测值时，所有风电场工作于“最大出力模式”；当调度指令低于风电预测值时，处于弃风限电状态，此时风电场工作于“计划功率模式”。通过各层递阶优化，得到场群层以及风电场层在每一调度周期的计划值。

图4 场群层及风电场层功率计划值Fig.4 Power plan values of field group and wind farm layer

图5—图8分别为W1～W4风电场在文中所提分层控制方法下的出力值以及在传统固定比例、变比例控制下的出力值对比。

图5 W1控制结果Fig.5 W1 control results

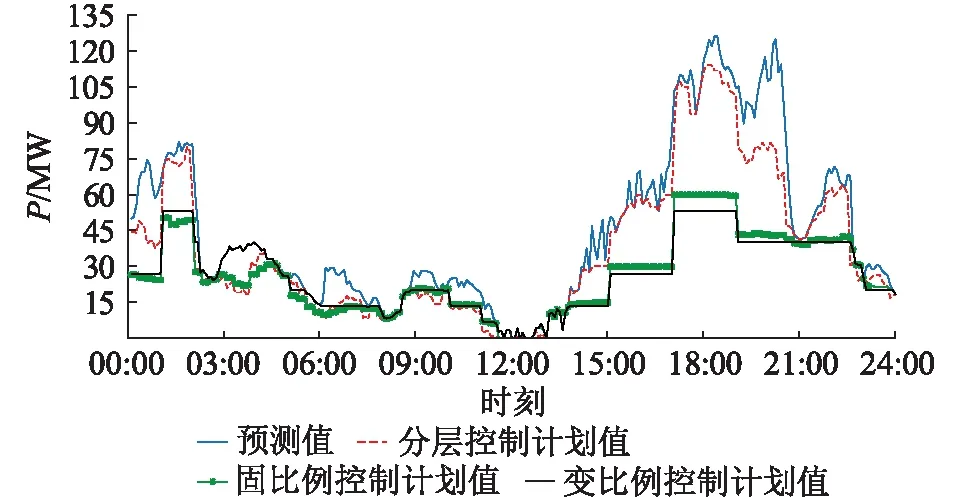
图6 W2控制结果Fig.6 W2 control results

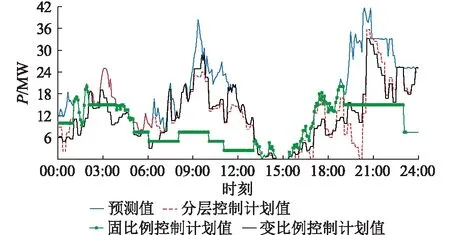
图7 W3控制结果Fig.7 W3 control results

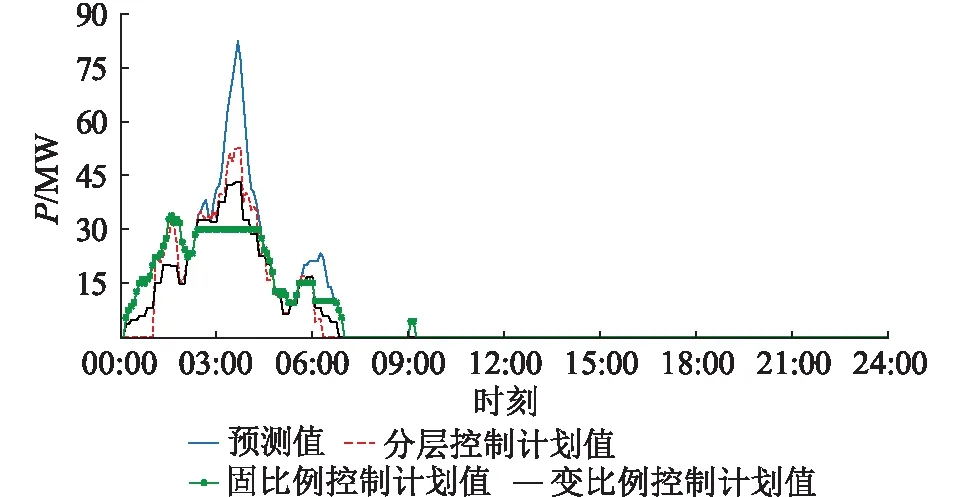
图8 W4控制结果Fig.8 W4 control results

由图5—图8对比分析可知，由于固定比例控制方法未充分利用风电的超短期预测，W3风电场在09:00—12：00风电预测出力较高时未分配更多的出力计划，造成了一定的弃风，而按风电机组在下一调度周期的预测值进行有功功率分配的变比例控制相比固定比例控制在一定程度上减少了弃风。分层控制相比于变比例控制又在更短的时间尺度内，通过超短期风电功率预测对各风电场有功出力进行优化分配。由于调度时间接近预测时间，分层控制在分配风电出力上更加精确，弃风量相比变比例控制进一步降低。

将分层控制与传统固定比例、变比例控制的弃风率进行对比，结果如表2所示。

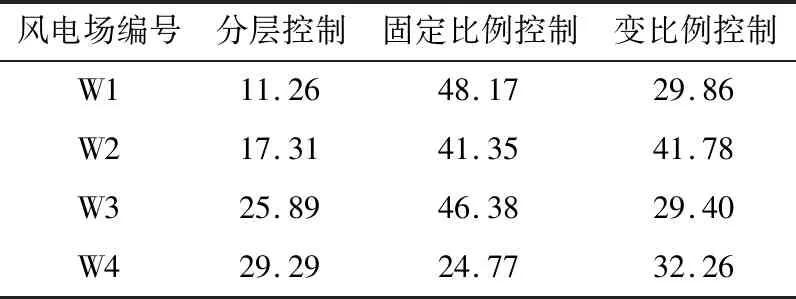
表2 不同控制方法弃风率对比Table 2 Wind curtailment rate comparison of different control methods %

根据表2可计算出3种控制方法的总弃风率分别为20.12%，41.23%，37.15%。分层控制的弃风率相对于变比例控制减少了17.03%，相对于固定比例控制减少了21.11%。可见，文中所提分层控制方法相对传统控制方法在减少弃风、提高风电消纳率上成效更加显著。

5.2 机组层算例分析

机组层调控的主要目的是减少风机调控次数，进而减少风机机械损耗，提高风机使用寿命。由于在风电机组降功率场景下需要频繁调节桨距角，甚至切机，文中算例只分析降功率场景下风电机组的调控状态。

风电场W2由8排共100台风力发电机组组成，每台功率为1.5 MW。以同一排风机为单位调节对象，分析其在一个降功率调度周期，风电场出力由83.88 MW下调至61.38 MW时，采用文中排序控制方法与传统变比例控制方法的各排风机动作情况。各调控指标在该调度周期的权重如表3所示。各排风机调控能力综合评分及所对应的机组状态如表4所示。

表3 各调控指标所占权重Table 3 Weight of each control indicator %

表4 各排风机调控能力及机组状态Table 4 Control ability and unit status of wind turbines in every row

对于降出力场景，弱出力机组为最后动作的机组，若可调机组都调至最低限额时仍无法满足需要下调的功率总和，则从弱出力机组开始进行切机操作。在该调度周期内，风机的调控次序为G7，G5，G6，G4，G8，G2，G3。G1为弱出力机组，不考虑对其进行调控。采用文中排序控制方法与传统变比例控制方法的各排风机出力如表5所示。

表5 各排风机出力Table 5 Output of wind turbines in every row MW

由表5可知，文中所提排序控制方法从调控能力高的机组开始下调出力，当下调至G4排风机时满足风电场下调功率要求，此时总动作排数为4排；而对于变比例控制，除了弱出力机组G1外，其余7排机组都动作，总动作排数为7排。可见，文中采用的排序控制方法能够有效减少风机调控次数。

6 结论

文中提出了考虑风机排序控制的风电集群分层有功控制方法，得到如下结论：

(1) 风电集群分层控制更好地利用了风电超短期预测技术，使调度指令更加合理地下发给各场群以及各风电场，有效提高了风电消纳量。

(2) 比较风电机组排序控制与传统变比例控制可知，风机排序控制能够有效减少风机调控次数，从而减少风机机械损耗，提高风电场的经济效益。

文中所提考虑风机排序控制的风电集群分层有功控制方法能够在提高风电消纳量的基础上减少风机调控次数，对实际风电场运行时的有功功率控制有一定的参考价值。

本文得到国网山西省电力公司电力科学研究院项目“适应特高压交直流混联电网的新能源协同控制策略研究”(52053018000N)资助，谨此致谢！