基于Optistruct的电池包结构分析与优化

刘成武，吴平，李喆，施京凯，吴铭

(福建工程学院 机械与汽车工程学院，福建 福州 350118)

纯电动汽车的核心为电池、电机和电控系统[1]。电池包是纯电动汽车的储能装置，要求有足够的强度和刚度，其约束模态必须能够避开由电机和路面不平度引起的共振。为了更长的续航，电池包体积不断增加，不少纯电动汽车轴距越来越长，导致动力电池上盖面积增大、刚度不足的现象时有发生。针对电池包进行各种极限工况和约束模态仿真分析，研究其刚度和强度的分布情况，在工程应用中具有一定参考价值。

1991年，Kazuo Ao[2]便开始对电池包的设计和分析。1995年，Krawczuk[3]对电池包做模态分析。2011年，Ariyoshi Tomohik[4]对新能源汽车动力系统建模与仿真的研究。之后国外出现了一些用有限元方法研究电池包的文章[5-8]。国内也有类似的研究，兰凤崇、王振坡和崔佳等人[9-11]用有限元技术对电池包的轻量化、碰撞安全性和振动疲劳等进行研究。但目前的研究还存在一些不足，如文献[12]对电池包进行有限元分析，但连接关系和电池模组都过于简单，不能充分模拟各种工况下电池包内部各部件之间力的传递过程。

本文以某纯电动汽车电池包为研究对象，模拟真实情况下电池包内部的连接关系，搭建更精确的有限元模型。

1 电池包精细化建模

电池包由箱体、电池模组、托架、电气系统元器件、热管理系统元器件和冷却系统等部分组成。将电池模组简化为一个均质长方体，建立模组与侧板之间固定的长螺栓。保留模组底部的水冷板和模组与模组之间的软连接。由于电器件、高压插件、霍尔传感器、继电器、水冷管、输电线等一些塑料件刚度、强度对整体影响不大，为了减少计算量，将它们以质量点的形式施加在相关单元上。

动力电池模组采用六面体网格划分，其他均采用壳单元划分，六面体单元尺寸为8 mm，壳单元尺寸为10 mm。有限元模型如图1所示，主要材料、属性及厚度见表1。本文主要对电池包进行静力学工况分析，电池未发生失效，故采用均质化模型。

图1 电池包有限元模型Fig.1 Finite element model of the battery pack

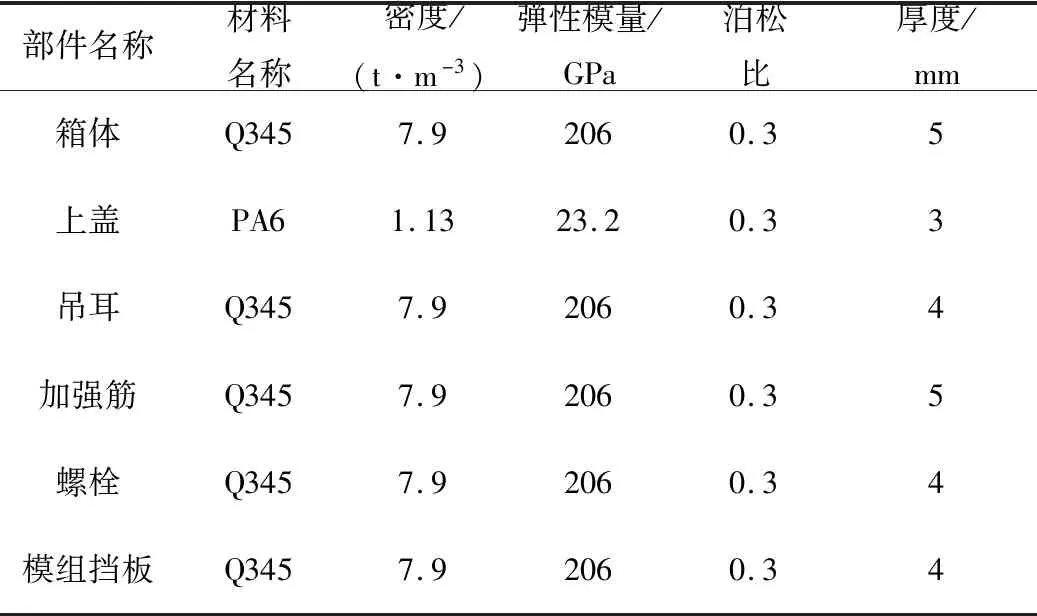
表1 材料参数Tab.1 Material parameters

焊点采用ACM单元如图2(a)所示，引入实体单元提高计算精度，同时rb3单元不会提高刚度。螺栓由rbe2单元和cbeam单元组成如图2(b)所示，能够较好地模拟真实情况中螺栓的固定作用。最终模型共计1 374 252个网格，1 507 302个节点，雅可比小于0.6的网格只有246个远小于5%，总质量450.7 kg与实际质量误差小于5%。模型用于仿真分析。

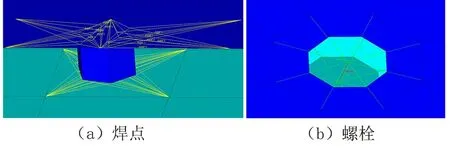
图2 焊点和螺栓建模形方式Fig.2 Modeling of solder joints and bolts

2 静力学典型工况分析

电池包通常占用纯电动汽车质量的1/3，在静力学典型工况中主要受振动载荷及惯性力的作用。为了考察电池包的动力学特性，对电池包在颠簸、刹车、加速、急转弯等典型工况下进行分析，判断是否具有足够的强度和刚度，以及是否能够抵抗复杂的加速度和惯性力，从而确定电池包是否达到对电池模组和电器系统的保护作用以及模组是否受损。

参考文献[13]选取颠簸路面急转弯和颠簸路面急刹车两种典型工况对电池包进行分析。边界条件加载方式列于表2，其中车辆前进方向为X-，驾驶员左侧方向为Z+，垂向为Y+，其中Y向的加速度包含重力加速度。

表2 典型工况及加载方式Tab.2 Typical working conditions and loading methods

电池包通过10个螺栓与车身相连，为了更好地模拟电池包与汽车的真实连接情况，在螺栓孔周围建立一圈washer，然后用rbe2单元抓取，约束rbe2单元所有自由度。

上盖主要起封闭作用，不作为这两种工况下的主要讨论对象。为避免rbe2单元刚度太高，导致部分吊耳螺栓孔附近应力集中，隐藏与rbe2单元直接相连的washer网格，对吊耳，箱体，加强筋、电池模组等部件进行分析。

2.1 颠簸路面急刹车工况

在颠簸路面急刹车工况下，对电池包施加边界条件为约束吊耳rbe2单元所有自由度。载荷条件为在Y向施加3g加速度，在X向施加3g加速度。结果如图3所示。

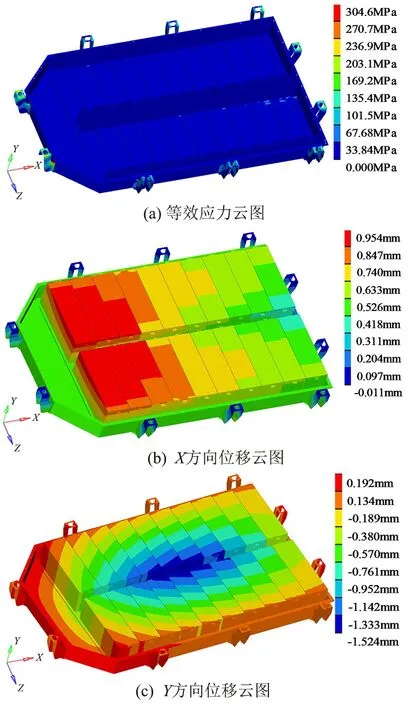
图3 颠簸路面急刹车工况应力、位移云图Fig.3 Stress and displacement cloud diagram of sudden braking conditions on bumpy roads

由图3(a)可知，在颠簸路面急刹车工况下，承受应力最大的部位是吊耳与箱体的连接处，应力为304.6 MPa，吊耳所采用的材料是Q345钢材，其屈服值为345 MPa，所以在颠簸路面急刹车这种极限工况下，电池箱体安全，没有零部件发生屈服。

王芳等[14]评价电池包静力学特性指标为：在3g的加速度作用下，结构件的变形不应超过3 mm。从图3(b)分析得到，在颠簸路面急刹车的工况下，电池包X方向上电池模组发生的最大位移不超过1 mm，由图3(c)可知，在Y方向上位于电池包中间的模组发生上下颤动，最大位移1.52 mm，小于3 mm。综上，该电池包在颠簸路面急刹车工况下结构安全。

2.2 颠簸路面急转弯工况

在颠簸路面急转弯工况下，对电池包施加边界条件为约束电池包吊耳所有自由度。载荷条件为在Y向施加3g加速度，在Z向施加2g加速度，仿真结果如图4所示。

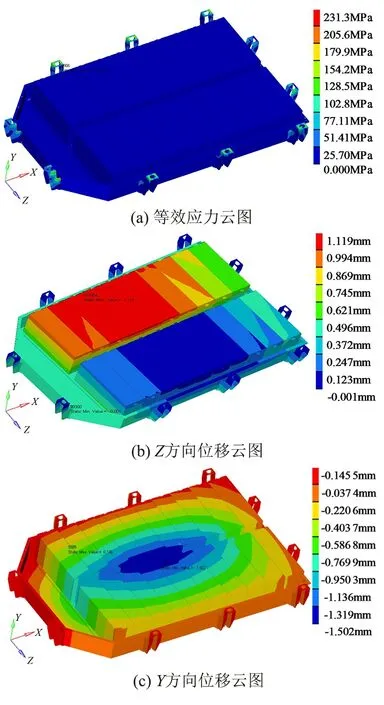
图4 颠簸路面急转弯工况应力、位移云图Fig.4 Stress and displacement cloud diagrams of sharp turning conditions on bumpy roads

由图4(a)可知，电池包在吊耳与汽车固定处出现应力最大值231.3 MPa，小于345 MPa。由图4(b)可知，模组Z方向最大位移为1.119 mm。由图4(c)可知，在Y向加速度作用下，电池模组发生了颤动，Y向位移量为1.5 mm，根据文献[14]中的评价指标，该电池包在颠簸路面急转弯工况下结构安全。

3 约束模态分析及优化

3.1 电池包约束模态分析

约束模态求解分析数学模型及求解过程如下：

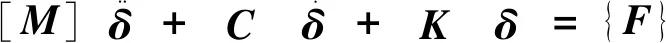
(1)

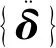
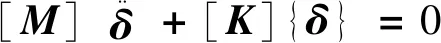
(2)

自由振动的相应振型和固有频率

{δ}={δ0}sin(ωx+Ø)

(3)

带入简化可得：

([K]-ω2[M]){δ}=0

(4)

自由振动情况下：

([K]-ω2[M])=0

(5)

解出n个实根ω2i(i=1,2,3,…,n):

ω21≤ω22≤…≤ω2n

(6)

提取电池包前6阶约束模态，振型如图5所示，具体振型描述及频率见表3。

表3 约束模态振型及频率Tab.3 Vibration modes and frequencies of the constraint mode

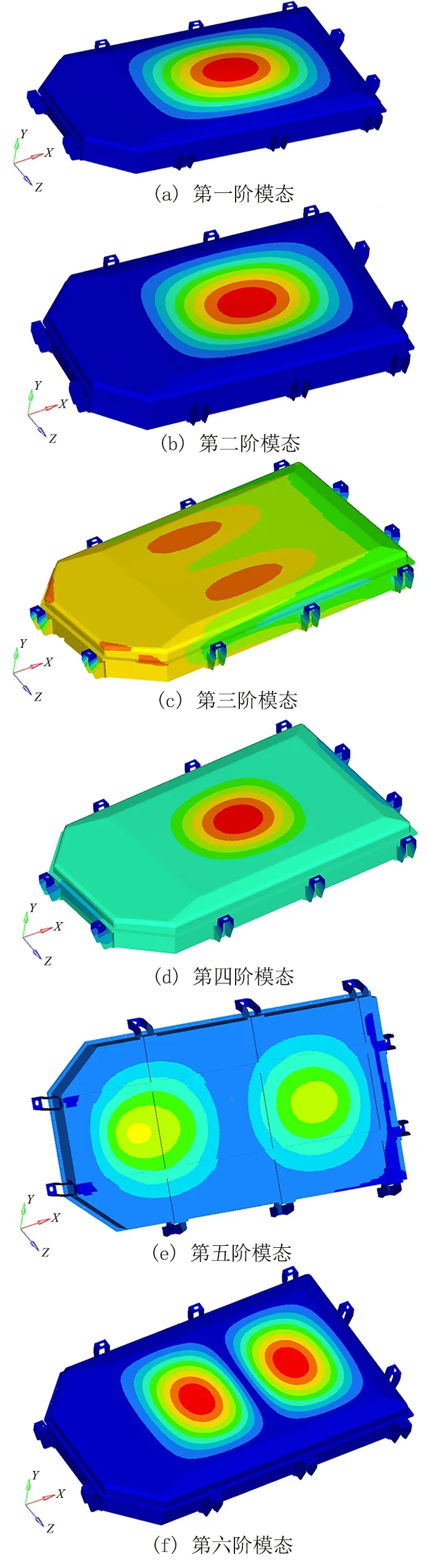
图5 前6阶约束模态Fig.5 The first 6-order constraint modes

纯电动汽车的主要激励来源于地面不平度和和电机运转，通常电机产生的激励小于20 Hz。所以主要考虑路面不平度引起的加速度和位移激励，电池包的一阶频率应该高于由路面不平度引起的激励。式(7)为路面激振频率计算公式。

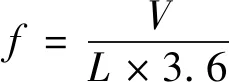
(7)

式(7)中，V为行驶车速，km/h；L为路面不平度波长，m。表4列出了国内常见路面的激振频率[15]。

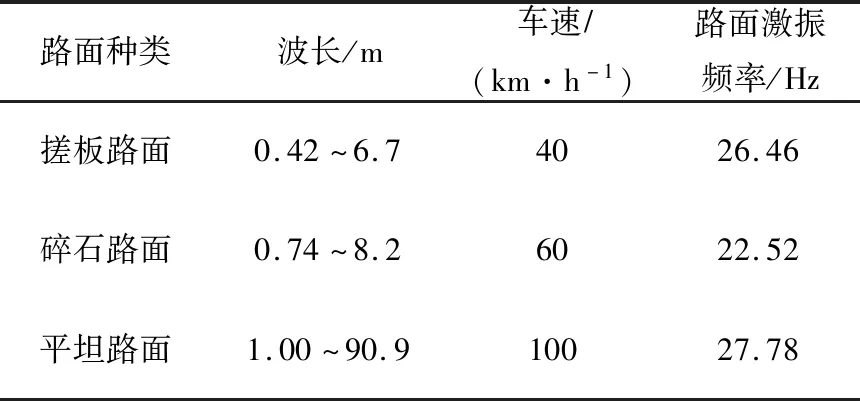
表4 常见路面的激振频率Tab.4 Excitation frequencies of common road surfaces

从表4可知，为了避免共振，电池包一阶频率应该高于27.78 Hz。从表3得出，电池包前两阶频率都低于27.78 Hz，且第二阶频率与平坦路面下的激振频率极为接近，提示上盖刚度不足，应该进行优化。

3.2 电池包上盖拓扑优化

优化思路：现有动力电池上盖多为复合材料，采用模压成型，厚度容易控制，且控制成本较低。由于上盖刚度较弱，导致电池包一阶约束模态频率偏低，通过厚度优化设计，提升电池包一阶约束模态频率。拓扑优化数学模型如下：

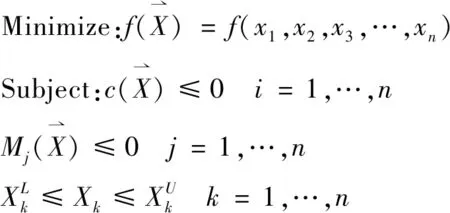
(8)

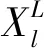
图6 优化结果Fig.6 Optimization results

红色区域厚度为4 mm，以此为参考，重新在Creo软件中设计上盖，将重新设计的电池包模型进行有限元分析，优化后的一阶约束模态如图7所示。

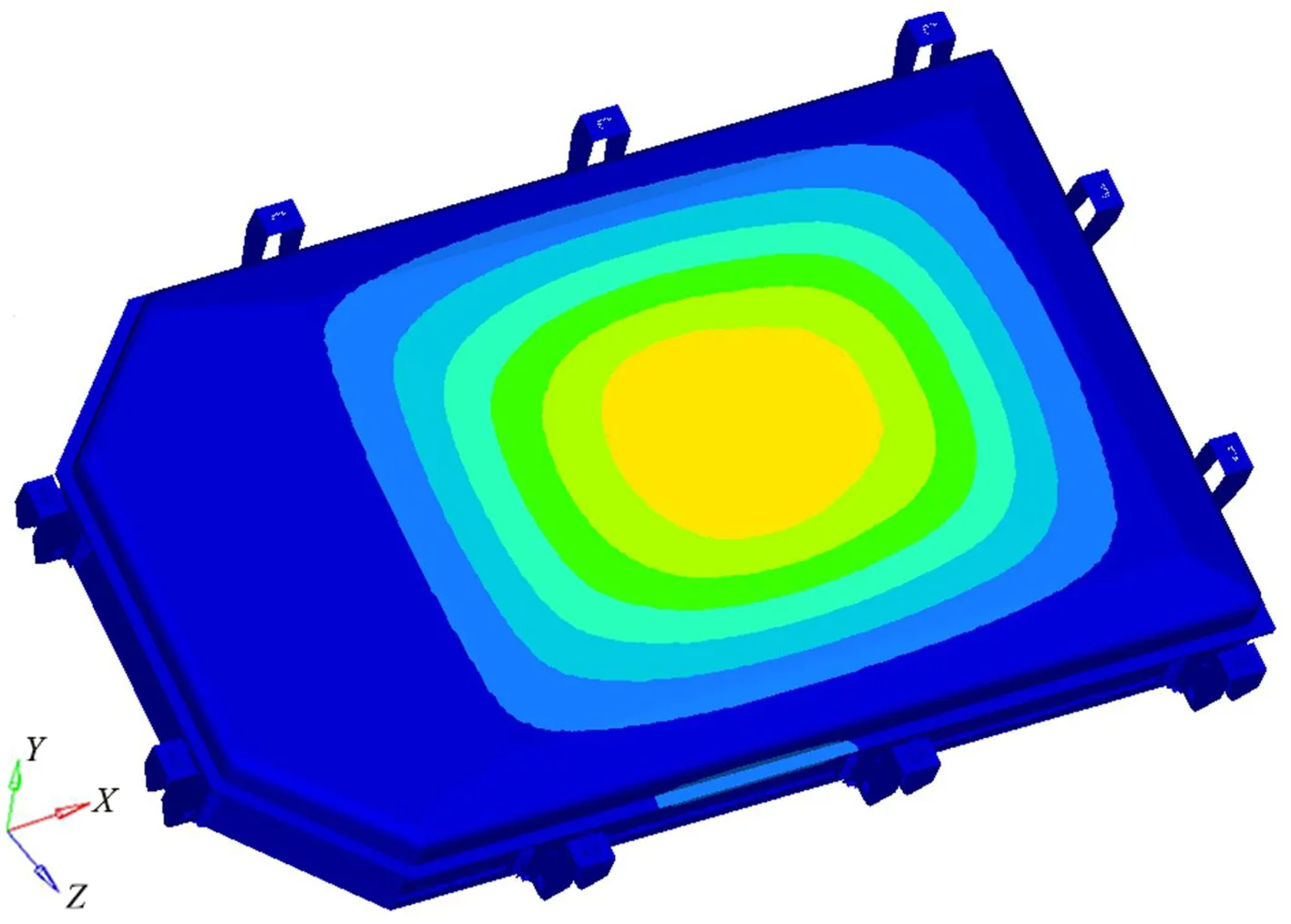
图7 优化后一阶约束模态28.4 HzFig.7 The optimized first-order constrained mode 28.4 Hz

对优化后的模型进行约束模态分析，得出第一阶频率为28.4 Hz，高于27.78 Hz，有效地避开了路面的激振频率。图8为优化前后电池包前6阶约束模态频率对比，相比于优化之前频率都有提高。优化厚度之后上盖质量增加1.58 kg，对整车影响较小。

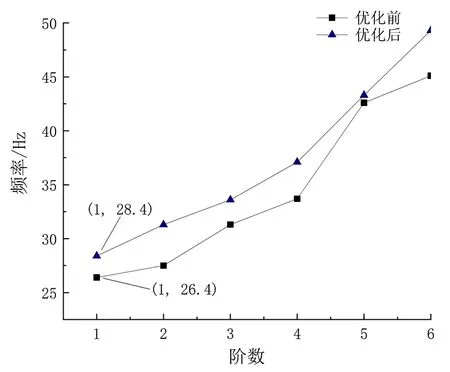
图8 优化前后前6阶约束模态频率Fig.8 The first 6 constrained modal frequencies before and after optimization

4 结论

本文模拟了该动力电池两种极限工况，得出电池包在这两种工况下均满足条件。提取电池包前6阶约束模态，分析得出第一阶频率较低，上盖刚度较低，与地面的激励形成共振且对电池模组发生干涉，对电池造成危害。

运用拓扑优化方法，对上盖进行厚度优化设计，经过4次迭代，优化后一阶频率达到28.4 Hz，高于27.78 Hz ，改进了上盖的刚度，提高了一阶频率，避开路面的激振频率。提升了电池包的动力学性能，为结构设计优化提供参考。