法兰直线轴承视觉测量递阶式规划与行为分析

李纪强,孔令华,花海燕

(1.福建工程学院 机械与汽车工程学院，福建 福州 350118；2.福建工程学院 数字福建工业制造物联网实验室，福建 福州 350118)

直线轴承是一种广泛应用于精密机床、纺织机械、包装机械等工业机械的关键运动部件。方法兰系列是其主要系列之一，同系零件具有特征相似性高但尺寸规格多样的特点。采用视觉技术进行孔系特征测量时，由于视野范围与特征尺寸关系的不同，导致测量方案、检测过程存在差异，测量行为也存在多样性选择，对测量结果的影响复杂。当前，关于视觉测量的应用研究已取得不少成果[1-3]。针对微小零件的视觉测量误差因素主要包括光学成像误差、计算方法误差、标定误差和噪声误差等[4]。对于尺寸较大的零件，视野无法包容全部特征，工位变换不可避免[5-6]，特别是有多特征、多视角测量需求的零件，检测流程因待测项增多、特征空间分布复杂性增大等因素，增加了测量过程的复杂性[7-8]。有的研究利用双相机进行多工位图像的采集与拼接完成产品尺寸测量[5]，有的将工件分解为多个部分采集[6]，也有研究采用线阵相机等进行薄板件多孔特征的测量[9]。分析现有研究发现，视觉检测过程呈现明显的测量方案多样性和图像处理过程行为多样性的特点，尤其是面向系列化零件检测需求时，往往无法实现对全系列零件采取完全一致性的测量行为；即使对同一零件，可能会因测量过程处于不同视野区域、需多节拍采集图像或者采取不同图像处理算子等行为因素的差异，而造成测量结果的影响波动。结合实验设计和量化评估，获取测量方法和测量数据可靠性信息是视觉测量过程非常重要的工作[10]。测量过程的行为多样性必然对测量结果造成复杂的影响，要实现自动化、高可靠性测量，有必要进行测量行为的规划。由于不同法兰系列的直线轴承孔系尺寸检测存在很大共性，故本研究以方法兰系列为对象，从待测特征与视觉野包容关系分析入手，阐述测量规划策略，并开展孔系尺寸测量过程行为分析工作。

1 面向系列化零件的递阶式视觉测量规划

1.1 零件族孔系特征包容方案规划

方法兰直线轴承的孔系特征包括轴承中心孔和法兰连接孔。虽然不同系列包含的孔数相同，但尺寸及位置关系不同，采用面阵相机测量时，必然会因视野与工件尺寸关系不同，导致测量工位和测量行为发生变化。为实现自动视觉测量，首先分析不同尺寸零件与视野的包容关系，进行孔系特征包容方案规划。本研究重点讨论至少包容两孔的情况，按照最大包容原则进行包容方案规划。对某系列的方法兰直线轴承与可视区域进行包容关系分析，归纳6类包容关系见表1所示，每类包容情况仅列出一种位姿的图例。

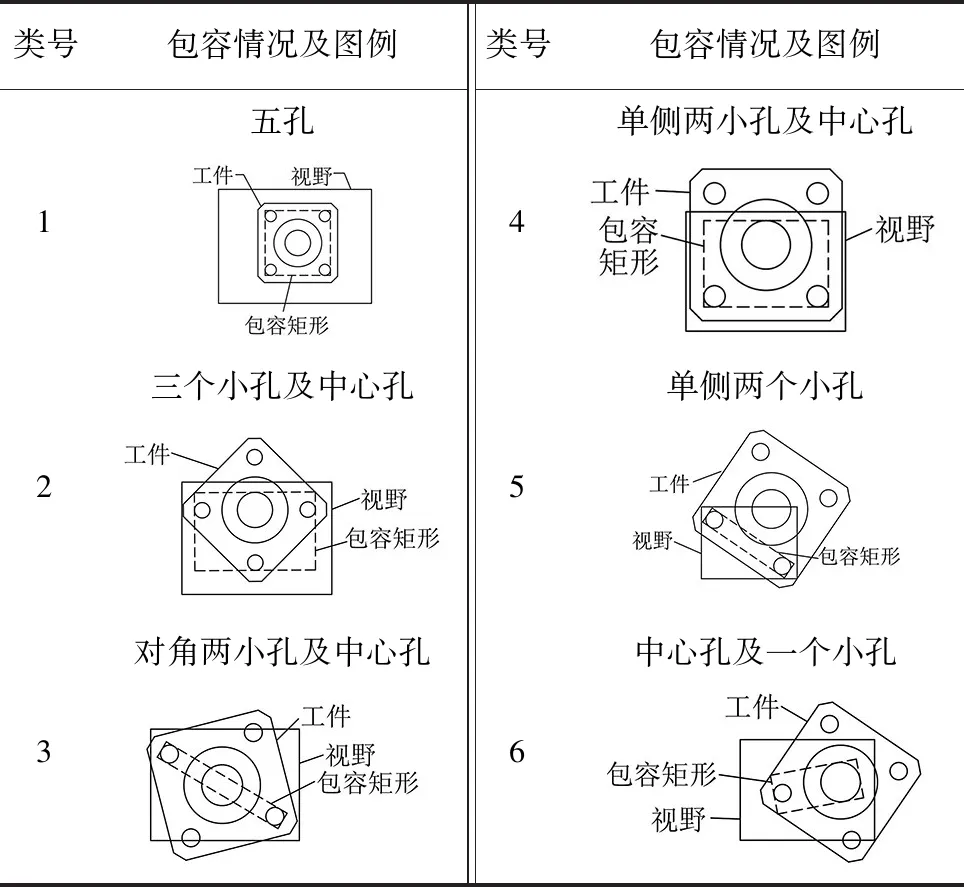
表1 零件与可视区域包容关系分类Tab.1 Classification of the containment relationship between parts and visible areas

根据包容关系建立包容方案规划事件处理环节，具体如下：

(1)获取待测零件设计尺寸：Dr，D，DP，d1，待测零件设计信息见表2。

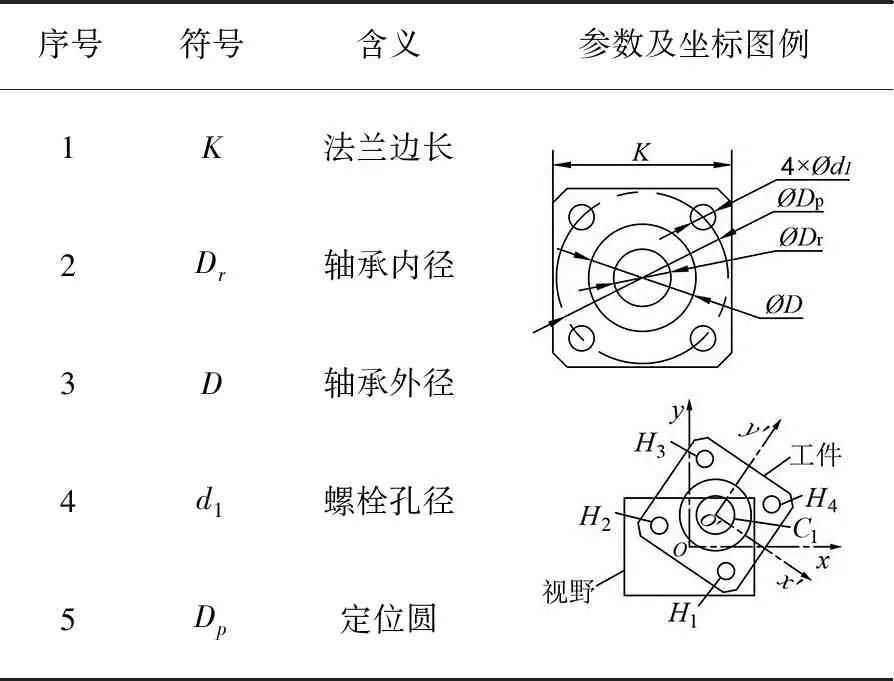
表2 待测零件设计信息Tab.2 Design information of tested parts

(2)确定可视区域。获取相机、镜头参数，计算理论视野，设置视野预留余量Δa，计算实际可视矩形区域的长度L和宽度W，建立可视区域坐标系Oxy，如表2图例所示。

(3)建立孔系特征矩形。各类包容关系仅列举与表1图例对应的特征矩形建立规则，见表3。

表3 孔系特征矩形的建立规则Tab.3 Rules of establishing characteristic rectangle for holes

(4)最大包容关系判定。根据可视区域与孔系特征矩形，判定两个矩形的包容关系，确定待测零件与可视区域最大包容关系类型。

(5)根据所判定的最大包容类型，规划工件坐标原点O′相对测量区域坐标系Oxy的理论位姿方案，工件坐标系O′x′y′如表2图例所示。

1.2 基本动作规划

为完成零件中全部孔特征测量，当确定的包容关系类型不同时，所需要变换工位的次数和变换动作存在差异；同一类型包容关系下的孔系特征矩形也可能存在多种建立规则；对应同一规则下的包容关系，工件坐标原点O′相对测量区域坐标系Oxy还存在多种位姿方案；当待测零件和理论视场的变化，还可能影响同一位姿方案下工件的移动允许偏移量和旋转角度允许偏移量。可见，面向零件族孔系测量时，工位变换路线及工位关系均存在多样性。但分析发现，多样性的工位路线存在着动作共性，为此，对测量行为进行基本动作规划，以实现测量路线的灵活组合配置。

从工件位姿在可视区域中的行为动作看，可将其看作对心找正，x向平移，y向平移，对心旋转，偏心旋转等基本行为动作的组合。工位变换基本动作对应参数如表4所示。以工件坐标系相对可视区域坐标系的参数xO′、yO′、θ作为动作位姿参数，x0、y0、θ0是动作前后需维持的位姿参数取值；行为变量是运动控制变量，根据可视区域和孔系特征矩形的关系，规划动作行为变化和区间约束，其中x1、y1、θ1为新位姿工件坐标系原点在可视区域坐标系的坐标，Δx、Δy、Δθ为其单侧允许偏移量。通过位姿参数和行为变量的规划，提高基本动作在不同规格零件中的适应性，通过基本动作的同时执行，可衍生复杂的行为动作。

表4 基本动作对应参数Tab.4 Parameters of basic actions

1.3 基本工位变换路线规划

对于不同尺寸的零件，可能一次采集图像就能包容全部孔特征，也可能需要在同一包容类型中进行多次变换工位，还可能涉及多种最大包容类型才完成测量，且工位变换的方案具有多样性。为此，在基本动作基础上，根据表1的包容关系基本路线分为两类，第一类路线主要针对一次测量能测得全部孔特征的情况，第二类路线是以孔系遍历为主要目的工位变换路线。

2 基于任务的视觉测量规划与行为评估流程设计

面向系列化尺寸检测需求，待测零件型号规格的变化引起测量行为变化，测量方案的多样性又对测量结果产生复杂的关联影响。为了获取测量行为变化对测量结果的影响波动，实现更可靠的测量，以任务需求为依据，设计了视觉测量规划与行为评估流程，如图1所示。整个流程分为方案规划阶段和行为执行及评估两部分。

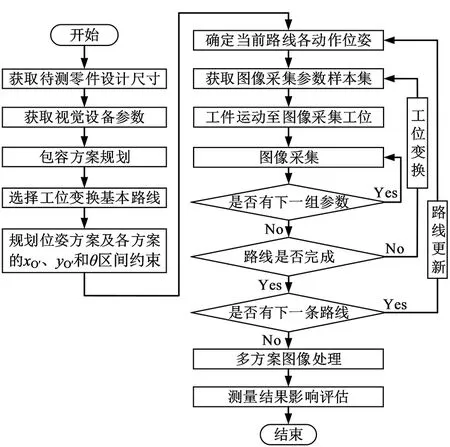
图1 视觉测量规划与行为评估流程Fig.1 Process of the visual measurement planning and behavior evaluation

3 测量实验与行为分析

3.1 多因素实验测量规划与行为影响分析

本研究以某型号方法兰直线轴承为测量对象，在视觉测量系统中，选用CCD相机与畸变小的远心镜头，搭建了背光源视觉测量系统。为了分析测量行为对测量结果的影响波动，设计实验任务1以法兰连接孔H1～H4为待测特征，以评估图像质量、拟合算子与工位变换动作的关联影响为任务。按照图1流程规划出表5。该规划匹配包容类型5，规划路线为前面提到的第二类路线，首先对心找正，然后x向平移和y向平移，最后进行偏心旋转，这样完成了一轮采集。此时再判断全部孔特征是否采集完成，若未完成，则循环偏心旋转，直到全部孔特征采集完成。其中偏心旋转角根据表1类号5包容矩形与视野关系，确定松弛条件，然后判断两圆孔可否包容在视野内部，得到如图2所示偏心旋转的两个极限工位。图2中，极限工位圆孔与视野相切，虚线段l1、l2为孔H1和H2圆心的连线段，分别求出l1和l2的垂直平分线与水平线的夹角θ1和θ2，则可求出偏心旋转的范围为[min(θ1,θ2), max(θ1,θ2)]。本实验通过计算旋转角区间，在所确定偏心旋转范围内，确定基本角度为从水平位置逆时针旋转55°，且逆时针旋转为正，使得工件坐标原点位于可视区域第一象限，并获得两孔容许工位1，而后依次逆时针旋转90°，获得工位2～工位4。

图2 偏心旋转极限工位示意图Fig.2 Schematic diagram of the extreme position of eccentric rotation

按表5规划的4个工位采集图像，每个待测孔都包含从左上区域变换到右下区域的动作事件。本实验所建立关联影响评估任务信息如表6所示，被评估项包括图像质量和拟合算子。图像质量由4个参数控制，即目标灰度、曝光、增益、亮度，课题组前期所研究得到的参数优选区间[11]分别为[55,157]、[283,393]、[231,286]、[35,847]，从中采用拉丁超立方抽样方法获得30组参数样本，以其为设置参数，共采集图像120张图片。对采集到的图片进行相同的灰度变换、预处理、图像边缘提取等图像处理操作，采用7种不同的算子拟合孔特征，分别测得孔径尺寸。

表5 实验任务1测量规划Tab.5 Measurement planning for experiment task 1

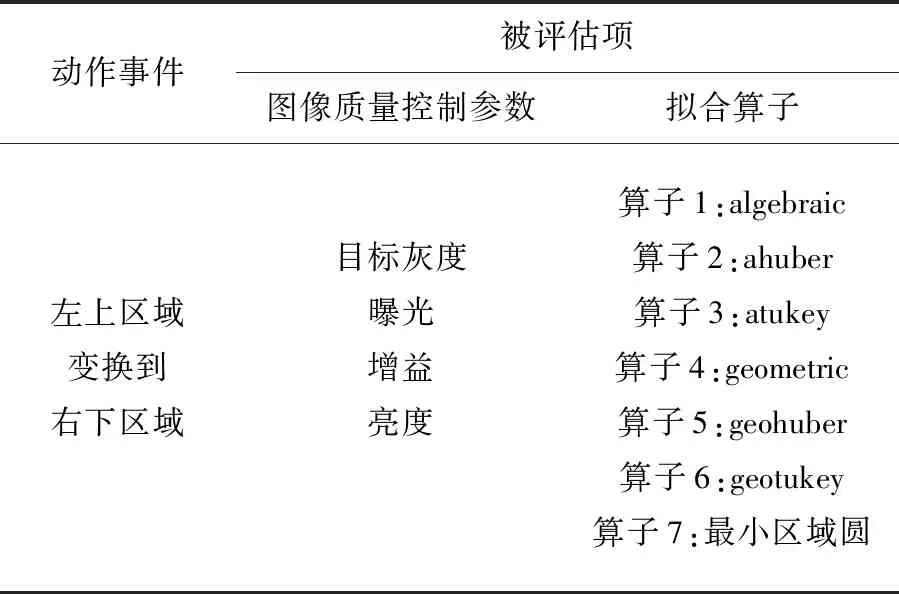
表6 关联影响评估任务信息Tab.6 Information of correlation impact evaluation task

以表6所示影响评估任务对实验任务1的孔H1～H4进行分析，每个孔特征以左上区域与右下区域孔的测量差值除以左上区域孔测量值的百分比表征动作事件变化对测量结果的影响波动，4个孔的影响波动情况如图3所示。

图3 任务1孔H1-H4工位变化测量影响波动Fig.3 Measurement influence fluctuation of H1-H4 with the working position changed in task 1

由图3可见，当4个孔做相同的动作变换时，测量结果波动随着图像质量的不同，提取各算子波动极差、均值、标准差信息进行对比，发现算子1、2、4、5波动重合度较高且波动极差小，归为优选算子；算子3、6、7波动极差较大，归另一类。综合观察4个优选算子在拟合孔H1～H4时的波动信息，其波动幅度大约在0.04%～0.09%范围，标准差在0.009%～0.021%范围，表明在工位变化时这4个算子受图像质量影响比较小，测量的稳定性较好。算子3、6、7波动幅度较大，表明工位变换时其受图像质量影响更敏感。以算子7为例，其波动幅度在0.13%～0.16%范围，标准差在0.027%～0.033%，算子3和算子6影响波动更严重。此外，算子6在测量不同对象时，还发生了波动均值偏移的现象，相比4个优选算子总体波动均值偏移了0.11%。为此，后续将以评估所得优选算子1、2、4、5作为拟合算子，开展分析实验。

为了进一步分析待测特征变化时，工位变化、图像质量和拟合算子三者的影响关系，设计实验任务2，进行孔C1和孔H1～H4的孔径测量。按照图1流程进行实验测量规划，匹配包容类型6，循环执行4次任务1的规划路线完成图像采集，按前述方法确定旋转角范围，并随机确定第一工位初始角度，而后其他工位按相对于轴对称选取。实验任务2测量规划信息见表7所示。

表7 实验任务2测量规划Tab.7 Measurement planning for experiment task 2

续表7

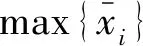
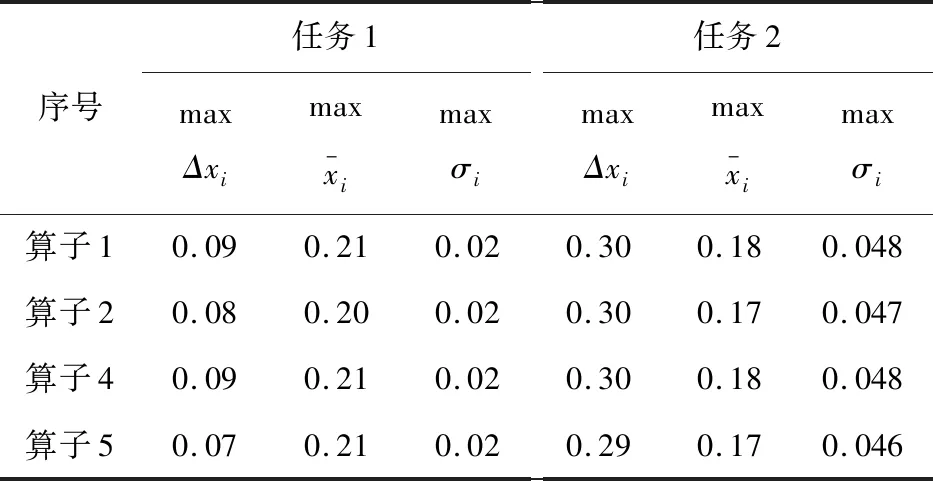
表8 任务1和任务2孔H1～H4测量波动影响对比Tab.8 Comparison of the measurement influence fluctuation for H1-H4 between task 1 and task 2

由表8可见，任务2中工位变化时4个算子对测量结果的影响波动极差整体变大，较任务1的扩大3倍左右，对比波动均值，任务2比任务1则整体略微偏小，相差不大。对比标准差，任务2的标准差为任务1的2倍左右。可见，对孔特征图像进行增强预处理的行为，会使工位动作变化时测量结果波动范围更大，且由于标准差扩大，其数据稳定性降低，造成算子稳定性随采集参数变化的图像质量变得更为敏感。

为进一步提取4个优选算子处理30组图像样本的波动信息，综合统计孔H1～H4测量中4个优选算子拟合的情况，发现处理孔H1和孔H3时，出现了个别样本的异常波动，以孔H1为例如图4所示。将30个参数样本用拉衣达(Pauta)准则[12]剔除异常点，孔H1～H4测量的极差范围0.08%～0.24%，均值范围0.17%～0.19%，标准差0.019%～0.040%。可见，综合4个孔的情况与任务2还是很接近，故个别异常值并不影响总体对比结果。从上述分析中还可以发现，当前的参数样本区间中，仍然存在个别图像质量较差，容易造成测量波动异常的样本，在后续测量中以30组参数样本中测量稳定性较好的参数样本组作为优选样本组，进一步做测量研究。

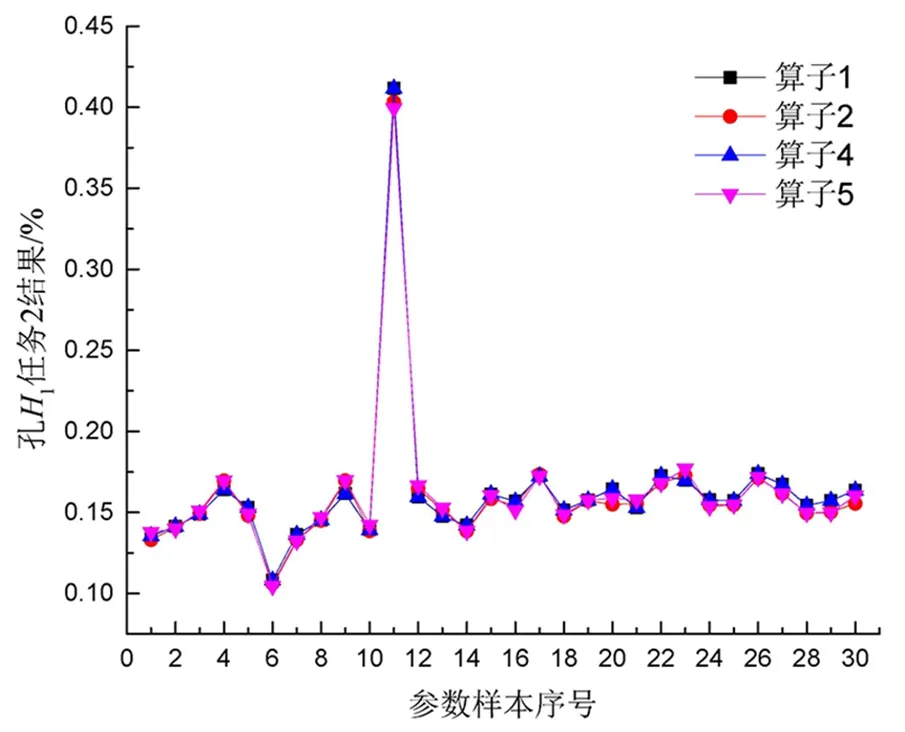
图4 任务2孔H1工位变化测量影响波动Fig.4 Measurement influence fluctuation of H1 with the working position changed in task 2

为了考察相同的工位变换动作，相同图像预处理处理算子、不同拟合算子对不同质量图像、不同特征的关联影响波动情况。首先，先对比4种优选算子对任务2中孔C1工位变换时的测量结果影响波动情况，见表9所示，工位变换动作及波动表征指标与任务1相同。由表9可见，待测特征改变时，4个优选算子对工位变换引起的测量波动情况仍然是一致的，并没有因为不同特征图像质量变化的差异性而影响其总体波动程度的一致性。

表9 任务2孔C1工位变化测量影响波动情况Tab.9 Measurement influence fluctuation of C1 with the working position changed in task 2

将表9与表8对比可以看出，任务2中孔C1相比孔H1～H4测量波动均值扩大了2倍左右，但波动极差和标准差相差不大。剔除孔C1异常样本极差范围0.12%～0.14%，均值范围(由于是负值，取绝对值)0.46%～0.47%，标准差范围0.029%～0.035%。可见，改变特征的测量行为，对于不同图像质量，算子稳定性改变不大，但是由于波动均值发生变化，会导致其波动偏移量增大。也就是说，当一个零件变换测量工位时，在采用相同图像处理算子的情况下，不同质量的图像样本，波动极差和标准差接近，故对零件上不同孔特征进行工位变换测量误差补偿时，需进行补偿量调整。

3.2 工位随机偏移测量实验与行为影响分析

在规划任务2时发现，按包容关系类号6进行图像采集，可视区域余量较大，测量工位允许变动范围也较大。为进一步获取测量行为的稳定特性，进行工位随机偏移测量实验(任务3)。图像采集仍采用表7的测量规划，在包容许可约束范围内(θ1介于10°～22°)随机变动，进行10次随机偏移测量，并设计工位随机偏移测量的误差削减行为评估任务，见表10所示。根据表8中的4个工位，图像采集参数在上述实验结果中优选一组参数样本，对各工位进行一轮全部孔特征图像采集，共获得160张图片。工位随机偏移测量行为对测量结果的影响见表11所示。

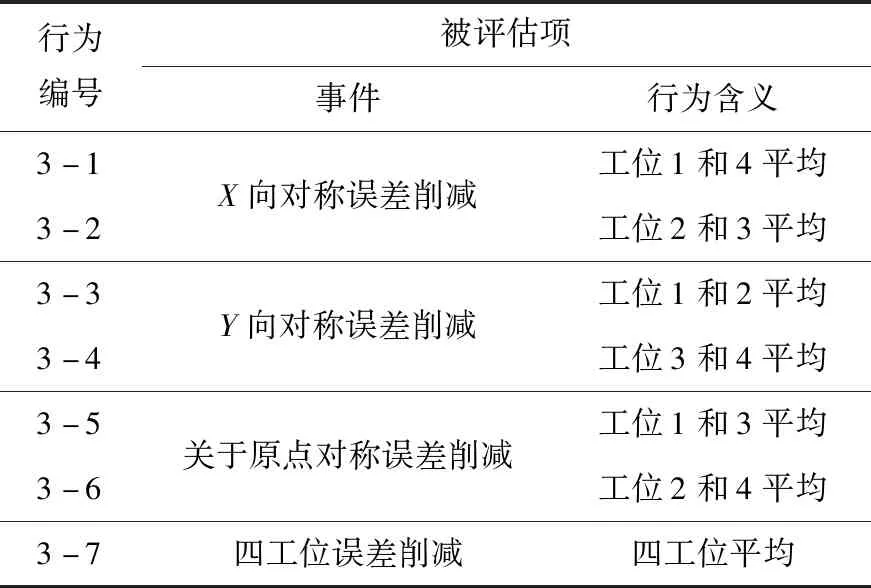
表10 任务3误差削减行为评估任务Tab.10 Evaluation for error-reducing behavior in task 3

对比表11中孔H1～H4四工位10次随机偏移测量所得最大值与最小值，发现四工位随机偏移测量波动极差分别为0.0165、0.0171、0.0181、0.0165 mm，折算为百分比平均为0.48%。四孔单工位10次测量均值的最大差异为6.5 μm，也就是说在优选的算子和参数下，对孔H1～H4在不同工位多次重复测量，测量均值差异在6.5 μm以内。若采用误差消减行为，不同处理方法所得结果最大差异仅有3.3 μm，行为处理后影响波动削减一半，且已在很小范围内波动，测量较稳定。

表11 任务3测量行为对测量结果的影响Tab.11 Influence of measurement behavior on measurement results in task 3 mm

将视觉测量所得孔H1～H4四工位随机偏移10次测量均值和上、下偏差与高精度大型工具显微镜测量结果进行对比，如图5所示。视觉测量均值相对于显微测量均值，偏移量分别为0.030、0.026、0.024、0.030 mm。表明孔H1～H4在多工位随机偏移测量时势必会造成测量波动，但若以四工位消减后均值作为孔的测量值，则相对显微测量，平均需要补偿量0.028 mm左右，该值可作为两仪器测量所需修正的系统补偿量参考值。

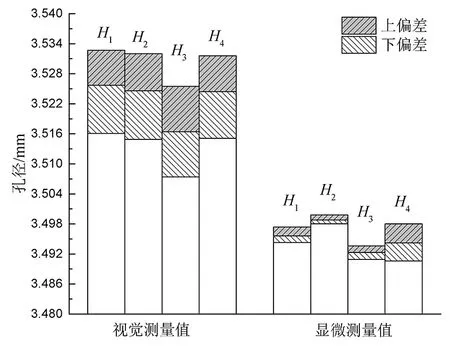
图5 孔H1～H4两种不同测量方法结果对比Fig.5 Comparison of results of two different measurement methods for H1～H4

同样，对孔C1工位随机偏移测量实验结果进行分析，四工位测量波动极差0.1303 mm，折算百分比值为1.62%，比孔H1～H4要敏感3倍左右。观察表12中工位变化误差削减行为，不同削减行为得到的测量结果有所差异，差异范围在25 μm以内，比孔H1～H4的3.3 μm大了近七倍多，但是若折算百分比值，则分别为0.31%和0.1%，也在3倍左右。将视觉测量所得孔C1四工位随机偏移10次测量均值和上、下偏差与高精度大型工具显微镜测量结果进行对比。四工位削减后均值为8.033 mm，与工具显微测量均值8.046 mm相比，偏移了-0.013 mm。但是若对比4个工位附近偏移测量的均值发现，工位3是正向偏移0.010 mm的，其他工位则是负向偏移的，且偏移量在-0.028～-0.016 mm，相比之下其工位随机偏移测量后会导致测量偏移不易补偿了。由此可见，对不同特征即使发生了相同的测量行为变化，所造成的测量影响波动敏感性是存在差异的。可以以上述行为波动的影响分析结果作为测量规划时的评定依据，优先满足更敏感的特征处于视场中优势工位或优先保障其行为稳定性，从而来提高测量结果的可靠性。

4 结论

1)通过递阶式测量规划与行为影响分析评估，便于获得视觉测量过程行为对测量结果的量化影响。考虑图像采集质量、采集工位和图像处理算法等多因素的综合影响，对提高视觉测量稳定性的改善是有利的。

2)本次实验通过对图像质量、算子和测量工位变化的关联影响评估，可实现拟合算子和图像采集参数的优选，为后续的实验提供指导。

3)由于特征与行为影响关系错综复杂，通过递阶式测量规划与行为分析，不仅可以确定行为变化对各特征测量结果的影响，还可以获得不同特征在相同行为变化时的受影响情况。获取多因素情况下波动误差幅度、波动偏移量、测量稳定性的量化信息，不仅有助于测量误差评估与误差补偿的实现，还可以作为测量规划决策的依据，其可促进视觉测量系统的前、后处理功能的增强。