例谈诱导公式的转化诱导功能

杜红全

(甘肃省康县教育局教研室 746500)

诱导公式是高中三角函数中的重要公式，利用诱导公式可以使看似复杂的三角函数问题得到巧妙的解答，起到事半功倍的作用.诱导公式充分体现了转化的数学思想，而转化的数学思想主要是通过诱导公式的诱导功能实现的.下面举例说明诱导公式的转化诱导功能.

一、利用公式转化诱导出所需要的“角”

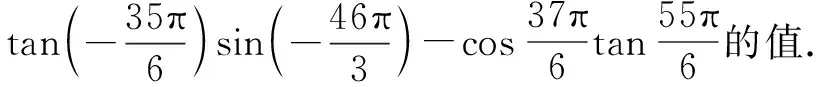
分析此题是给角求值问题，利用诱导公式转化导出特殊的锐角，然后运用特殊角的三角函数值求解.

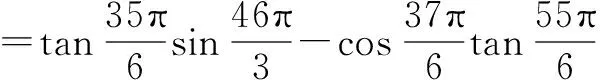
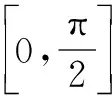
二、利用公式转化诱导出所需要的“函数名”

例2 求sin21°+sin22°+sin23°+…+sin289°的值.

分析不难发现1°+89°=90°，2°+88°=90°，…，44°+46°=90°,所以sin89°=sin(90°-1°)=cos1°，sin88°=sin(90°-2°)=cos2°，…，sin44°=sin(90°-46°)=cos44°，再利用公式sin2α+cos2α=1(α∈R)即可求解.

解析由1°+89°=90°，得sin89°=sin(90°-1°)=cos1°，所以sin21°+sin289°=sin21°+cos21°=1.

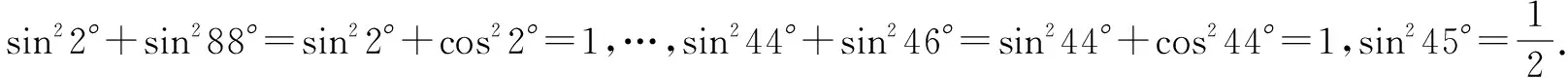
点评对于正、余弦的互余关系问题，都可用诱导公式转化诱导出所需要的函数名，即若α与β是互余角，则sinα=cosβ，cosα=sinβ.

三、利用公式转化诱导出所需要的“函数式”

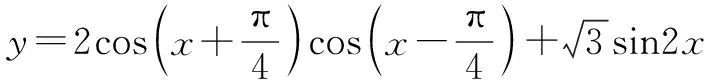
分析结合函数式的特点，利用诱导公式、二倍角公式以及辅助角公式，把函数式最终化为y=Asin(ωx+φ)+K的形式，然后再求最小正周期和最值.

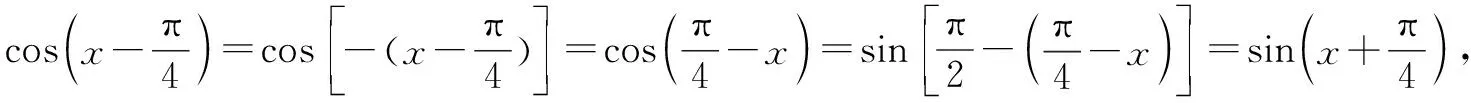
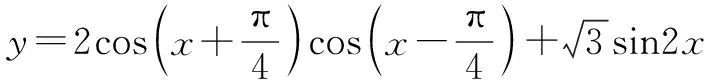
点评求解本题的关键是利用诱导公式、二倍角公式以及辅助角公式，把函数式最终化为我们需要的函数y=Asin(ωx+φ)+K的形式，体现了解题活动的目标意识.

四、利用公式转化诱导出所需要的“联系”

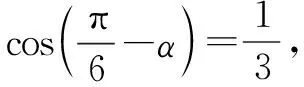
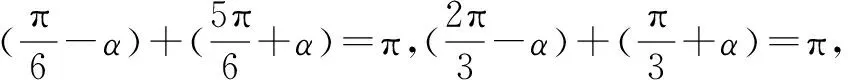
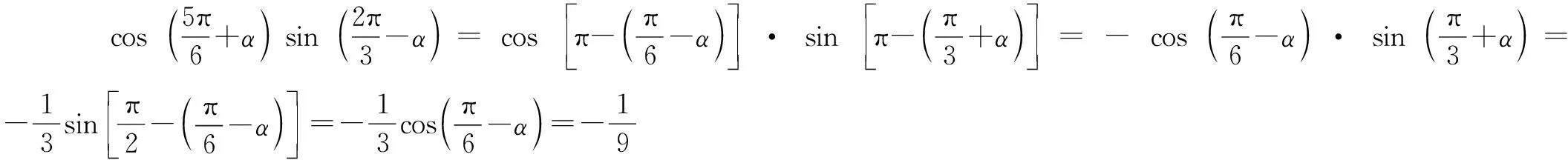
点评对于这类问题，要善于发现已知角和结论角互余(或互补)关系，充分利用诱导公式转化诱导出所需要的已知式和被求值式之间的关系.

例5 设函数f(x)=asin(πx+α)+bcos(πx+β)，其中a、b、α、β都是非零实数，且满足f(2019)=-1，求f(2020)的值.

分析根据已知条件，寻求f(2019)和f(2020)之间的关系，这个联系就是我们解答问题的关键.

解析因为f(x)=asin(πx+α)+bcos(πx+β)，f(2019)=-1，所以f(2019)=asin(2019π+α)+bcos(2019π+β)=-1.

所以f(2020)=asin(2020π+α)+bcos(2020π+β)

=asin[π+(2019π+α)]+bcos[π+(2019π+β)]

=-asin(2019π+α)-bcos(2019π+β)

=-[asin(2019π+α)+bcos(2019π+β)]

=-(-1)=1.

点评f(2020)和f(2019)是通过“π+α”的诱导公式联系转化沟通的.