基于高光谱特征指数的土壤有机质含量建模*

赵明松，谢 毅，陆龙妹，李德成，王世航

（1. 安徽理工大学空间信息与测绘工程学院，安徽淮南 232001；2. 土壤与农业可持续发展国家重点实验室（中国科学院南京土壤研究所），南京 210008；3. 矿山采动灾害空天地协同监测与预警安徽省教育厅重点实验室，安徽淮南 232001；4. 矿区环境与灾害协同监测煤炭行业工程研究中心，安徽淮南 232001）

连续的土壤高光谱曲线包含较多的波段和丰富的光谱信息，能够综合反映多种土壤属性信息，能够用于高效精确地土壤属性预测建模[1-5]。传统的土壤有机质（Soil Organic Matter，SOM）含量测试方法较繁琐且成本高，利用高光谱技术可以满足大量样本的SOM 含量快速精确测定的需求[6-8]。国内外学者利用可见-近红外反射高光谱（350～2 500 nm）技术在土壤属性的建模预测方面开展了较多的研究。

由于成土环境的差异，不同地理区域和类型的土壤高光谱特征存在差异，已有研究分别结合土壤类型、区域等建立了多种SOM 含量光谱预测模型[5，8-11]。史舟等[5]分析了中国主要土壤类型的高光谱反射特性，并提出了采用土壤光谱分类方法结合偏最小二乘回归方法建立SOM 的光谱分类-局部预测模型。张娟娟等[8]研究了我国中、东部地区5 种土壤类型的光谱特征，并利用特征光谱参数和神经网络建立SOM 的预测模型。赵小敏和杨梅花[10]分析江西省4种主要土壤亚类的高光谱特征，并尝试利用光谱特征进行土壤分类。邬登巍和张甘霖[12]讨论了母质和土地利用类型对SOM 光谱反演模型精度的影响以及模型的异地适用性。

不同的光谱变换处理[13-17]、建模和验证样本集的划分[18]会影响SOM 预测模型的精度。光谱变换处理通过增强土壤在某些波段的吸收或反射特征，从而提高土壤属性光谱建模的精度等，研究表明使用光谱预处理后模型精度优于原始光谱数据模型[13]，根据不同波段范围采用不同光谱变换处理，能够提高模型的稳定性和预测能力等[15]。于雷等[14]认为采用连续统去除变换结合偏最小二乘回归模型是江汉平原SOM 含量的最优预测模型。王一丁等[17]对比了3种光谱变换处理后建立的潮褐土的SOM预测模型的精度。基于不同建模方法的SOM 光谱建模研究较多，其中偏最小二乘回归模型总体精度较高，应用较广[6，19-22]。Shi 等[2]提出了一种基于空间约束的局部偏最小二乘回归模型，并利用中国土壤光谱库精确预测了SOM 含量。Viscarra Rossel 和Behrens[19]利用偏最小二乘回归、多元自适应回归样条等7 种算法预测了SOM 和黏粒含量等，对比评估了模型精度以及结果的可解释性。纪文君等[20]利用多种数据挖掘技术建立了浙江省水稻土SOM 预测模型，并与偏最小二乘回归模型进行了对比。上述研究多是利用全谱段的光谱数据进行土壤属性的预测建模。土壤高光谱曲线包含波段较多，且波段间有不同程度的相关性，存在一定的信息冗余。

提取土壤光谱特征指数，一定程度上可以减少土壤属性光谱建模输入变量，提高建模效率，是土壤属性光谱建模的另一种思路。构建或计算光谱特征指数的方法有很多，如两两波段组合的代数运算（如比值、差值等）、弓曲差等计算相对较简单、方便。此外，还有基于光谱吸收特征的计算稍微较复杂，如吸收谷深度，吸收带宽、面积等。张娟娟等[8]利用光谱反射率通过波段间代数运算提取了比值指数（Ratio Index，RI）、差值指数（Difference Index，DI）和归一化差值指数（Normalized Difference Index，NDI），选出与有机质相关系数最高的特征指数建立SOM 估测模型，表明利用光谱特征指数预测SOM含量精度较高。贺军亮等[23]通过计算有机质诊断指数建立了SOM 线性回归预测模型，预测结果较好。卢艳丽等[24]利用1 280 nm处反射峰高度较好地预测了东北地区主要土壤类型有机质含量。彭杰等[25]利用吸收峰总面积、最大吸收深度、面积归一化最大吸收深度等光谱特征，建立了新疆地区土壤盐分含量的光谱预测模型。

苏中平原系江苏省长江和苏北灌溉总渠之间的广阔平原，属江淮平原的一部分，主要包括泰州、扬州、南通和淮安等大部分市县。该区地处北亚热带，水热条件充裕、土壤肥沃，是江苏省主要的粮食生产基地之一。本研究以苏中平原的典型土壤为研究对象，进行可见光-近红外高光谱采集和有机质测定，分析土壤光谱特征，计算弓曲差、光谱特征指数等建立SOM 预测模型并进行分析，为快速有效测定苏中平原SOM 含量提供技术支持。

1 材料与方法

1.1 研究区概况

研究区位于江苏省中部平原（119°53′37″～120°14′4″ E，32°20′17″～32°44′50″ N），主要包括姜堰市和兴化市南部（图1），面积约为1 350 km2。研究区属暖温带北亚热带季风气候，年平均气温14.5 ℃，降水量991.7 mm，海拔5～10 m。成土母质主要为泻湖相沉积物和长江冲积物，分布在研究区北部和南部，主要土壤类型为水稻土和潮土。研究区土地利用以水田为主，占总面积的81.25%（2009 年），轮作制度主要为稻-油（麦）轮作。

1.2 土壤样品采集与测试

土壤样品采集于2009 年11 月，共采集表层（0～20 cm）土壤样品178 个，其中水稻土111 个，潮土67 个。在田块的中心以10～20 m 为半径（S 形）取8～12 个土壤样品，然后将采集的土壤样品混合在一起并用四分法留下1 kg，同时记录田块中心的坐标信息。

样品在室内经自然风干后用木棒碾磨，剔除砂砾及植物残体，然后过10 目和60 目筛，前者用于光谱测试，后者用于有机质测试。采用重铬酸钾（K2Cr2O7）氧化滴定法测定有机质含量。

运用ASD FieldSpec 3 地物高光谱仪测量土壤样品的反射光谱数据，其波长范围为350～2 500 nm，重采样间隔为1 nm，输出波段数为2 151。操作过程在黑暗环境的实验室进行，光源使用仪器配套的两个1 000 W 的卤素灯，光纤探头视场角为5°，光源照射方向与垂直方向夹角30°，探头到土样表面距离30 cm，取适量过10 目筛的土壤样品倒入盛样皿中，用玻璃稍稍压实，刮平整。每个样品旋转4次，每个角度扫描10 次，共40 次，取平均值作为样本光谱。详细的土壤光谱测试条件描述具体参见文献[8]。

1.3 土壤光谱特征指数构建

本研究主要采用以下光谱特征指数。

（1）弓曲差（C）。通过选取光谱曲线中550、600 和650 nm 处的光谱反射率计算，C值与SOM含量存在负相关，同时在550～650 nm 范围光谱曲线表现出平直状态[26]。公式如下[26-27]：

（2）土壤光谱指数。构建的土壤光谱指数有：DI、RI 和NDI 等[11]。

式中，R500、R600和R650代表500 nm、600 nm 和650 nm波段上的光谱反射率；Ri和Rj分别代表i和j波段的土壤光谱反射率。

1.4 建模与精度评价

为了保证一定的建模样本数量得到稳定的预测模型，本研究使用Kennard-Stone（KS）方法划分建模集和预测集，该方法普遍用于光谱数据的分析中，详细计算过程参见文献[18]。按照建模与验证样本的3∶1 数量关系，利用该方法选取133 个建模样本和45 个验证样本。

采用交叉验证和独立验证的方式评价预测精度，选取决定系数（Determination Coefficients，R2）、均方根误差（Root Mean of Squared Error，RMSE）和相对分析误差（Relative Percent Deviation，RPD）作为评价指标。R2的值越接近于1，RMSE 越小，说明模型的稳定性和精度较高。当RPD < 1.4 时模型的估算能力差；当1.4≤RPD < 2 时模型估测精度有所提高，能对样本进行粗略估测；当RPD≥2 时表明模型具有很好的预测能力[28]。计算公式如下：

式中，yi和表示样本i的实测值和预测值，表示平均值，n为样本数，SD 为预测样本的标准差。

1.5 数据处理与分析

本研究对原始光谱反射率进行光谱倒数对数变换（Inverse-log Reflectance，Log（1/R））和去包络线变换（Continuum Removal，CR），识别土壤属性与光谱反射率的敏感关系。倒数对数变换主要目的是扩大可见光区的光谱差异，避免背景噪音的干扰；去包络线变换可以有效提取土壤的光谱吸收特征，更加直观地观察土壤的光谱特征[25，29]。

基于原始和变换后的土壤光谱曲线，本研究首先综合分析不同SOM 含量梯度和不同土壤类型的光谱特征、以及SOM 含量与高光谱信息的相关性。其次，计算弓曲差、DI、RI 和NDI 等特征指数及其与SOM 的相关系数。最后利用筛选后的光谱特征指数，基于多元线性回归进行SOM 含量建模，并进行精度对比分析。

Log（1/R）变换在The Unscrambler 9.7 软件中完成，CR 变换在ENVI 4.8 中进行。KS 方法，DI、RI 和NDI 的计算以及相关系数等势图，在MATLAB R2012a 软件中完成。数据统计分析及绘图分别在SPSS 22.0 和OriginPro 9.0 中完成。多元回归建模及验证在The Unscrambler 9.7 软件中进行。

2 结果与讨论

2.1 土壤光谱曲线特征

研究区SOM 含量总体较高且变化范围较大，平 均 值 为 28.54±7.80 g·kg-1， 介 于 11.85 ～58.22 g·kg-1；变异系数为27.33%，属于中等强度变异。其中水稻土的SOM 含量平均为32.13±7.21 g·kg-1，潮土的SOM 含量平均为22.60±4.34 g·kg-1。水稻土的 SOM 含量变异较潮土稍大，其变异系数为22.44%，潮土为19.20%。

按照SOM 含量< 20 g·kg-1、20～30 g·kg-1、30～40 g·kg-1和> 40 g·kg-1区间，计算各区间内的土壤光谱反射率的平均值，得到研究区SOM 所有区间对应平均光谱反射率曲线（图2）。随着波长的增加，在可见光波段土壤光谱反射率值迅速增大，光谱曲线呈现较陡的状态；在近红外波段内土壤光谱反射率较高，但是反射率增加较平缓（图2a）。在1 400 nm、1 900 nm 和2 200 nm 处可以看出光谱反射率值出现不同幅度的升降。在原始光谱曲线中出现吸收特征并不明显，经去包络线处理后的光谱吸收特征明显增强，吸收谷深度加深（图2b），除了1 400 nm、1 900 nm 和2 200 nm 附近吸收谷更加突出外，在480 nm、660 nm、900 nm 附近也出现了较明显的吸收特征。在560～660 nm 总体上随着SOM 含量的增加吸收谷深度加深，吸收谷的面积增大；在480 nm、900 nm 和1 650～1 850 nm 处趋势相反，总体上随着SOM 含量增加，吸收谷变浅。可见通过CR 变换后，土壤光谱曲线的吸收特征更加突出，不同SOM 含量光谱曲线的差异得到增强。在近红外波段，主要受到NH，CH 和CO 等基团的分子振动的倍频与合频吸收影响[30]。1 400 nm 附近的吸收谷主要是受到土壤表面吸附水、黏土矿物O-H 晶格结构水等吸收引起，2 200 nm 附近主要存在Al-OH 黏土矿物（高岭石）的吸收带[5，19]。蒙脱石类矿物在1 900 nm 和2 300 cm 附近有较强的吸收带。

图3 为SOM 含量与不同光谱变换反射率的相关系数曲线。SOM 与原始光谱在全波段范围上均呈极显著负相关（P< 0.01），与Log（1/R）光谱呈极显著正相关（P< 0.01），相关系数绝对值均在0.4以上。在400～900 nm 波段相关性远高于其他波段，相关系数绝对值均在0.6 以上，最高接近0.7（图3a、b）。SOM 与CR 光谱，在可见光390～750 nm、近红外800～900 nm、短波红外1 450～1 700 nm 和2 200～2 400 nm 处，呈现不同程度的正或负相关，相关程度总体上小于原始光谱和Log（1/R）光谱（图3c）。研究区SOM 含量反演的敏感波段主要位于为400～900 nm，1 450～1 700 nm 和2 200～2 400 nm处，这与众多研究结果基本一致[8，11，15，20]。徐彬彬等[31]比较了去除有机质前后的土壤光谱反射曲线的差异，发现对有机质响应最大的区域主要在600～800 nm。以上分析结果表明，采用原始和Log（1/R）光谱进行研究区SOM 含量反演时，敏感波段主要位于可见光和近红外波段范围；若选用CR 光谱数据，敏感波段范围选择较广，可见光、近红外和短波红外波段范围均有覆盖。

分别选取水稻土和潮土中SOM 含量最小值、25%分位数、中位数、75%分位数和最大值所对应的光谱曲线进行光谱特征分析（图4）。两种土壤类型的原始光谱曲线总体趋势基本一致，光谱曲线在可见光范围内快速上升，在近红外波段范围内上升缓慢且较为平稳。总体上，随着SOM 含量的增加，两种土壤的光谱曲线逐渐变低平，光谱反射率值减小，反映出二者间的负相关性。潮土在可见光范围光谱曲线的斜率较大，水稻土的光谱斜率相对较小。腐殖质是土壤有机质的主体，腐殖质中胡敏酸的反射能力较弱，富里酸在黄红光部分反射率开始增强，徐彬彬等[31]研究表明不同地带的土壤尽管其有机质含量相同，但由于胡敏酸和富里酸的比值不同，也会使土壤有不同的光谱反射特性。这可能也是两种土壤类型光谱特征差异的一个主要原因。

2.2 基于弓曲差的SOM 建模

图5 为研究区原始光谱在600 nm 波段的弓曲差与SOM 关系。随着SOM 含量的增加，在550～650 nm 范围内原始光谱曲线逐渐趋于平直状态，弓曲差值逐渐变小。SOM 与原始光谱的弓曲差呈极显著负相关，相关系数为-0.66（n= 178，P< 0.01）（图6）。这与徐彬彬和戴昌达[26]、Zheng 等[27]的研究结果一致。计算Log（1/R）光谱和CR 光谱在600 nm波段的弓曲差，二者分别与SOM 呈极显著相关，相关系数分别为0.61 和-0.33（n= 178，P< 0.01）。

利用三种光谱数据的弓曲差建立研究区SOM含量的线性回归模型，结果见表1。基于原始光谱和Log（1/R）光谱的弓曲差的回归模型稍好，建模集的R2分别为0.45 和0.38，验证集的R2分别为0.37和0.36；两个模型RPD 分别为1.28 和1.26，模型的预测能力较差。基于CR 光谱的弓曲差的建模结果最差，其建模集和预测集的R2均不足0.1，RPD仅为1.06，模型预测效果较差。以上结果表明，单独利用弓曲差建立的SOM 回归模型，估测能力有限，最高仅能解释SOM 变异的37%。

Zheng 等[27]研究发现江苏滨海盐土SOM 含量与弓曲差呈极显著负相关，相关系数为-0.74（n=142，P< 0.01），利用4 种模型预测了SOM 含量，模型的R2介于 0.38～0.51，RMSE 介于 4.12～4.62 g·kg-1。高志海等[32]利用600 nm 和800 nm 波段的两个弓曲差预测了甘肃省荒漠地区SOM 含量，600 nm 弓曲的模型精度较高，验证集的R2为0.84，RMSE 为4.57 g·kg-1（n=53）。高志海等[32]认为可能由于SOM 含量增加光谱逐渐趋于饱和的原因，当SOM 含量较低时，预测值均高于实测值，而SOM含量较高时，预测值基本接近实测值。本研究利用弓曲差建立的SOM 预测模型的精度（除CR 光谱）与Zheng 等[27]研究相似，验证集的R2为0.37 和0.38，RMSE 为4.89 g·kg-1和4.95 g·kg-1。上述分析表明，利用原始和Log（1/R）光谱在600 nm 波段的弓曲差的SOM 预测模型解释能力有限。

2.3 基于土壤光谱指数的SOM 建模

图7 为研究区SOM 含量与光谱指数的相关系数等势图，不同数值表示两个波段组合计算的DI、RI 或NDI 与SOM 的相关系数绝对值。相关系数等势图清晰地展示出，相关系数较高的特征指数构成波段的分布范围。

表1 基于弓曲差的SOM 线性回归建模结果Table 1 Modeling via SOM linear regression based on DOA

在原始光谱数据中，SOM 含量与DI 相关性较高的波段组合主要分布在400～800 nm 和2 180～2 220 nm 处，相关系数绝对值均在0.6 以上（图7a）。相关性最高的 3 个波段组合为 2 215 nm 和2 202 nm、2 219 nm 和2 198 nm、2 217 nm 和2 199 nm 波段，相关系数分别为0.73、0.73 和0.72。SOM 含量与RI 和NDI 的高相关性的波段组合范围一致且较宽，在1 000～2 400 nm 之间，最大的3个相关系数值相同，均为0.68、0.68 和0.67，构成RI 和NDI 的波段组合也相同，分别为2 202 nm 和2 215 nm、2 203 nm 和2 214 nm、2 203 nm 和2 215 nm（图7b、图7c）。

在Log（1/R）光谱的相关性等势图中（图7d ～图7f），SOM 含量与DI 的相关性较高的波段组合主要分布在1 100～2 400 nm 处，相关系数绝对值均在0.5 以上。相关性最高的3 个波段组合为2 202 nm和2 215 nm、2 203 nm 和2 214 nm、2 203 nm 和2 215 nm，相关系数分别为0.68、0.68 和0.67。RI和NDI 的相关系数等势图分布相似，相关性较高的波段组合范围分布较窄，在2 180～2 220 nm 处。相关性最高的3 个波段组合均为2 215 nm 和2 202 nm、2 219 nm 和2 198 nm、2 199 nm 和2 217 nm，相关系数分别为0.73、0.72 和0.71。在CR 光谱的相关性等势图中，相关性较高的波段组合范围较窄，且分布较散，DI、RI 和NDI 与SOM 的相关性等势图分布一致（图7g～图7i）。3 种光谱指数与SOM 的相关性最高的波段组合均为2 223 nm 和2 182 nm、2 223 nm 和2 183 nm、2 171 nm 和1 877 nm，相关系数分别为0.71、0.70 和0.70。

图3a 显示，原始光谱在2 198 nm、2 199 nm、2 202 nm、2 203 nm、2 214 nm、2 215 nm、2 217 nm和 2 219 nm 处反射率与 SOM 的相关系数介于-0.44～-0.43 之间，经计算DI、RI、NDI 后与SOM的相关性显著提高，相关系数绝对值在0.67 以上。Log（1/R）光谱在2 202 nm、2 203 nm、2 214 nm和2 215 nm 处经计算DI、RI、NDI 后与SOM 的相关性显著提高；CR 光谱在1 877 nm、2 171 nm、2 182 nm、2 183 nm 和2 223 nm 处计算的光谱指数与SOM 的相关性也显著提高。这表明不同波段的光谱反射率经过适当的特征指数计算后，增强了光谱数据与SOM 的相关性，一定程度上提高了建模预测的精度。

在3 种光谱指数中，分别选择与SOM 相关性最高的前3 个指数，进行研究区SOM 多元线性回归建模及验证，结果见表2。在原始光谱中，由于RI和NDI 的波段组合及与SOM 的相关系数均相同，其建模结果也相同；在Log（1/R）光谱中，选择的RI 和NDI 的波段组合也相同，其建模结果相同。基于原始、Log（1/R）和CR 光谱指数模型中，除了原始光谱的RI 和NDI、Log（1/R）光谱的DI 预测模型精度较低外，其余的SOM 预测模型精度均相对较高，建模集的R2均在0.53 以上，RMSE 在5.5 g·kg-1以下，验证集的R2均在0.65 以上，RMSE 较低均不超过4 g·kg-1。基于CR 光谱指数的SOM 预测模型的建模集和验证集的R2较接近，表明该模型的泛化能力较高。总体上，基于3 种光谱数据和3 种光谱指数建立的9 个SOM 预测模型中，RPD 范围介于1.4～2，表明建立的回归模型能够粗略估算研究区的SOM 含量。9 个预测模型中，基于原始光谱的DI 回归模型的预测能力最优，其RPD 为1.98；CR光谱中基于DI 的SOM 回归模型的RPD 虽然稍低，但模型具有较高的泛化能力。

表3 为3 种光谱数据的DI、RI、NDI 分别结合弓曲差C，进行SOM 的回归建模结果。结果表明，由于利用了较多的光谱特征指数，研究区的SOM 建模精度总体有不同程度的提升，建模集的R2和RMSE 分别介于0.56～0.64 和4.98～5.50 g·kg-1，验证集的R2和 RMSE 介于 0.67～0.73 和 3.21～3.51 g·kg-1，较表2 的建模精度有较大提升。9 种SOM模型的RPD 均在1.78 以上，其预测能力较表2 的SOM 模型有不同程度的提升。基于CR 光谱指数和弓曲差的SOM 预测模型的泛化能力较高。

在表2 和表3 的建模结果中，分别选择R、Log（1/R）和CR 的光谱数据中最优的SOM 预测模型，绘制独立验证结果图（图8）。可以看出，回归模型的预测值与实测值之间均存在不同程度的偏离，在SOM 含量低于20 g·kg-1处，样本存在一定程度的高估现象；SOM 含量在20 g·kg-1以上实测值和预测值明显较接近，这与高志海等[32]研究结果一致。总体上，基于Log（1/R）光谱的RI 结合弓曲差的SOM预测模型在所有模型中相对最优，其预测值和实测值较均匀且集中分布在1∶1 线附近（图8e）。

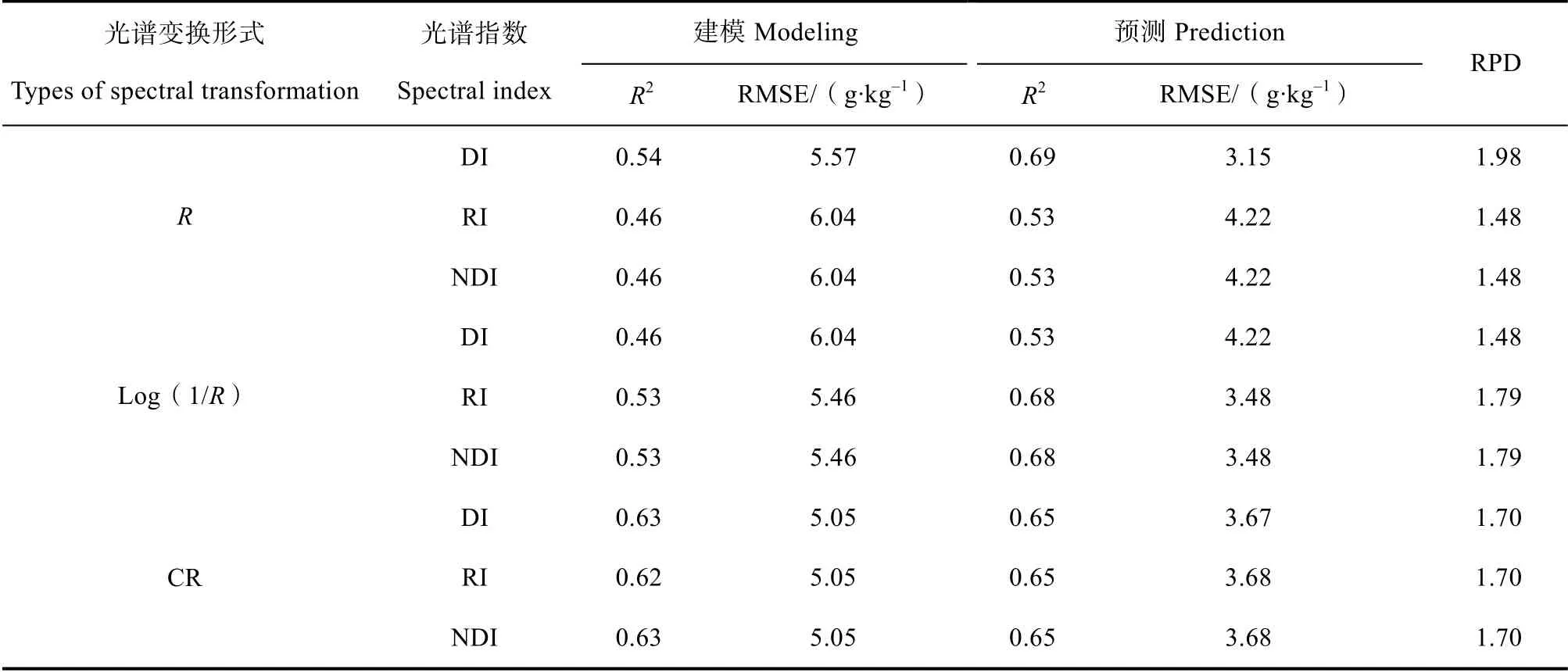
表2 基于光谱指数的SOM 建模结果Table 2 SOM modeling based on spectral indices

张娟娟等[8]研究认为光谱指数构成形式以DI 最好，其次为RI 和NDI。本文的结果显示对于原始和CR 光谱，DI 的建模效果较好；而对于Log（1/R）光谱，RI 和NDI 的建模效果较好，与张娟娟等[8]结论有一定程度上的相似。贺军亮等[23]采用DI 的计算思路，利用507～516 nm 反射率均值对450～750 nm反射率均值进行比值处理后获得有机质诊断指数，建立SOM 含量的预测模型精度较高，R2在0.65 以上，但是其样本较少（建模和验证样本分别为19 个和8 个）需要进一步研究。卢艳丽等[24]利用570～590 nm 波段的一阶导数光谱和1 280 nm 处反射峰高度较好地预测东北地区主要土壤类型有机质含量，但是其建模和验证的R2差别较大，训练集和验证集的R2分别为0.41～0.47 和0.72～0.75。沈掌泉等[33]认为光谱数据经过波段算术组合处理后，能降低模型建立过程中产生过配的风险，使模型能包括更多的成分和信息，其研究表明通过RI 或NDI处理后的光谱数据可以提高SOM 预测的精度。本研究利用光谱特征指数建立的SOM 预测模型建模和验证的R2均在0.6 以上且差异较小，能够解释研究区SOM 变异的65%以上，精度较高模型相对稳定。

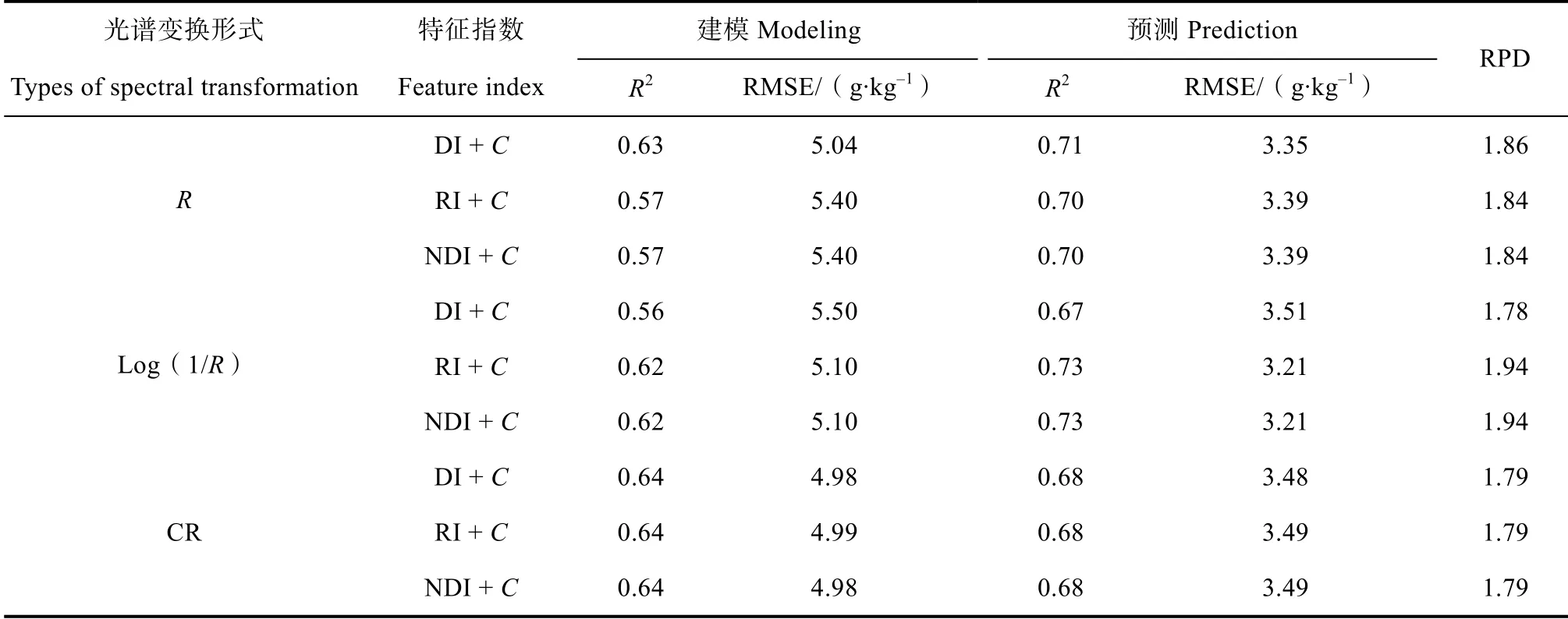
表3 基于光谱指数和弓曲差的SOM 建模结果Table 3 The results of modeling SOM using spectral index and deviation of arch

本研究依据SOM 与光谱指数相关性排序进行筛选建模，选择的光谱组合均在短波红外2 200 nm波段附近，但实际上研究区的SOM 含量与其他谱段范围内计算的光谱指数的相关性也较高。如原始光谱数据，在400～800 nm 波段范围计算的DI 与SOM相关系数绝对值均在0.6 以上（图7a）。在可见光、近红外和短波红外波段范围，土壤的光谱会反映不同的土壤组分信息，因此在后期的研究中尝试在不同波段范围内分别按照土壤属性与光谱指数的相关性等级，选取光谱指数进行预测建模。此外，本研究选取的光谱特征形式单一，在后期的研究中需尝试进一步构建或计算多种光谱特征指数，比较不同类型的光谱特征指数的建模效果。

3 结 论

（1）江苏省中部平原，不同SOM 含量和不同土壤类型的光谱曲线特征在全波段范围内变化趋势基本一致。去除包络线处理后，土壤光谱曲线特征差异明显，在480 nm、660 nm、900 nm 和1 800 nm 附近出现了明显吸收谷。SOM 与原始光谱呈极显著负相关，与Log（1/R）光谱呈极显著正相关，且在400～900 nm 波段相关性较强。SOM 与CR 光谱，在可见光390～750 nm、近红外800～900 nm、短波红外1 450～1 700 nm 和2 200～2 400 nm 处，呈现不同程度的正或负相关。（2）原始光谱和Log（1/R）光谱在600 nm 波段的弓曲差与SOM 含量呈极显著相关，能够解释研究区36%的SOM 变异，模型的RPD 分别为1.28 和1.26，模型预测效果差。（3）原始光谱、Log（1/R）光谱和CR 光谱等不同波段的反射率经过DI、RI 和NDI 特征指数计算后，增强了光谱数据与SOM 的相关性，一定程度上能提高建模预测的精度。选择不同光谱数据的DI、RI 和NDI 等指数建立的SOM 模型能够解释53%～69%的SOM 变异。将DI、RI 和NDI 等指数分别结合弓曲差，建立的SOM 预测模型效果最优，能够解释研究区67%～73%的SOM变异。其中Log（1/R）光谱的RI 和NDI 结合弓曲差的SOM 预测模型精度最高。