基于Petri网的前台业务流程建模及优化分析

林逢润 方 欢

(安徽理工大学 数学与大数据学院， 安徽 淮南 232001)

目前，业务流程模型管理在各个行业中都发挥着重要作用，比如银行、医院、餐厅和政务服务大厅中采用的挂号排队服务。但现有流程模型往往存在一个问题，即被叫号客户如果临时离开了，前台会一直等待直至等待时间结束，然后再依序叫下一个客户的挂号。这期间后面的客户需要等待，相应的服务窗口也会闲置，从而降低了办事效率和客户体验。

基于Petri网对现实中业务流程的建模及优化的研究已经取得许多成果。文献[1]基于Petri网建立了银行贷款业务排队服务模型。文献[2]基于Petri网建立门诊排队服务模型，并基于行为轮廓进行模型优化，以提高工作效率、缩短患者排队时间。文献[3]基于Petri网对共享雨伞使用流程进行建模，优化了共享雨伞的借用流程。文献[4]提出了基于Petri网可达性的生产流水线系统优化分析方法，解决自动化生产过程中出现的次品问题，有助于提高生产效率和产品合格率。文献[5]提出了含测试弧和抑制弧的增广Petri网，并分析总结了带测试弧Petri网的基本行为特征。借鉴有关研究成果，本次研究，我们以Petri网的行为轮廓、可达性和测试弧为基础，针对客户行为和前台办理业务流程进行建模分析与优化，并给出优化后的Petri网模型。

1 有关概念简介

(1) 流程模型。一个流程模型Petri网是一个四元组PN=(P，T；F，C)，并且满足条件：

PN=(P，T；F，C)；

P∩T=Ø；

P∩T=Ø；

F⊆(P×T)∪(T×P)；

dom(F){x∈P∪T|∃y∈P∪T:(y，x)∈F}；

dom(F){x∈P∪T|∃y∈P∪T:(x，y)∈F}；

C={and，xor，or}，是流程网的结构类型[6]。

由此可以得到，PN=(P，T；F，C)的基本元素集合分别是P(库所)和T(变迁)，在Petri网中分别用圆圈和方框表示。

(2) 可达性。已知Petri网PN=(P，T；F，C)，如果存在t∈T，使得[t>M′，则称M′为从M直接可达的。

(3) 行为轮廓。假设(N，M0)为一个网，其初始标识是M0，∀(t1，t2)∈(T×T)，满足如下关系：

若t1>t2且t2≯t1，则称严格序关系，记为t1→t2；

若t1≯t2且t2>t1，则称严格逆序关系，记为t1→-1t2；

若t1≯t2且t2≯t1，则称排他关系，记为t1+t2；

若t1>t2且t2>t1，则称交叉序关系，记为t1‖t2。

将满足以上关系的集合称为网系统的行为轮廓[6]，记作：BP={→，→-1，‖，+}。

(4) 测试弧。设含测试弧的Petri网是一个五元组Σ=(P，T；F，I，M)。其中：N=(P，T；F)是一个网；M是网的一个标识；I⊂S×T称为测试弧集，I∩F=Ø，即∀s∈S∧∀t∈T:(s，t)∈F→(s，t)∉I。

对于∀t∈T，若指向它的是测试弧，有：

∀s∈S:(s，t)∈F→M(s)≥1

∃s∈S:(s，t)∈I→M(s)≥1

则t在标识M处有发生权[5]，记为M[t>。

如图1(a)所示，除了基本的弧之外，有一条由s0连接到t0的测试弧，此时t0具有发生权。t0发生后的网结构如图1(b)所示。t0的发生并不会消耗s0中的Token，只是起到检测作用。图1(c)中的t0不具有发生权，因为s0中不含有Token。

图1 含测试弧的Petri网∑1

如图2(a)所示，此时的t0具有发生权。图2(b)中的t0则不具有发生权，因为它的输入库所s4中不含有Token。

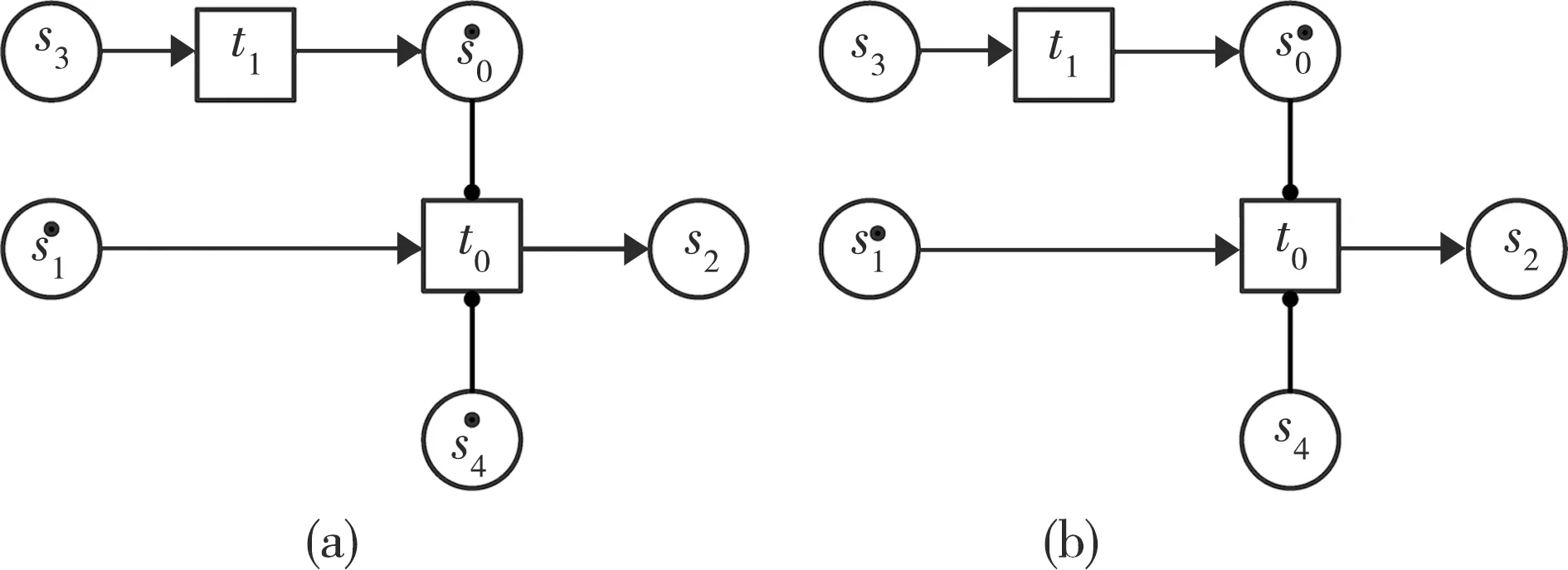
图2 含测试弧的Petri网∑2

为了增强Petri网的模拟能力，提出改良测试弧的概念。定义：含改良测试弧的Petri网是一个五元组Σ=(P，T；F，Z，M)。其中：

N=(P，T；F)是一个网，M是网的一个标识；

Z⊂S×T，称为改良测试弧集；

Z∩F=Ø，即∀s∈S∧∀t∈T:(s，t)∈F→(s，t)∉Z；

对于∀t∈T，若指向它的是改良测试弧，有：

∀s∈S:(s，t)∈F→M(s)≥1

∃s∈S:(s，t)∈Z→M(s)≥1

则t在标识M处有发生权，记为M[t>。

将图2所示Petri网模型中的测试弧，使用改良后的测试弧进行替换。根据定义，当s0或s4任意一个库所中含有至少1个Token时，则变迁t0均具有发生权。如图3所示，此时图3(a)和(b)中的t0均具有发生权。

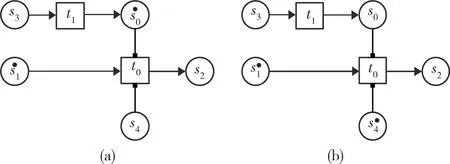
图3 含改良测试弧的Petri网∑3

2 前台业务流程模型优化

2.1 构建流程模型

建模是为模拟客户和前台工作人员的行为，因此依据实际情况做如下假设。

(1) 客户挂号完成后，或者因紧急事件而离开；或者一直在等待区等待。

(2) 客户离开后，不再对叫号进行应答。

(3) 客户处于等待区，叫号后，默认为在等待时间内应答。

(4) 客户挂号后的行为选择(留下等待或离开而放弃等待)是在前台工作人员呼叫该号之前完成的。

基于上述情况，以一位顾客办理业务的行为和前台工作人员处理一次客户业务为基础进行Petri网建模，分为客户视角与前台工作人员视角(见图4)。图中，库所s表示客户或前台工作人员的状态；变迁t表示客户或前台工作人员的活动。a、b线指示改良测试弧，其主要作用为约束变迁t4，使其在s2或s3中有Token时才能发生，即客户活动完成的时间先于工作人员开始活动的时间。

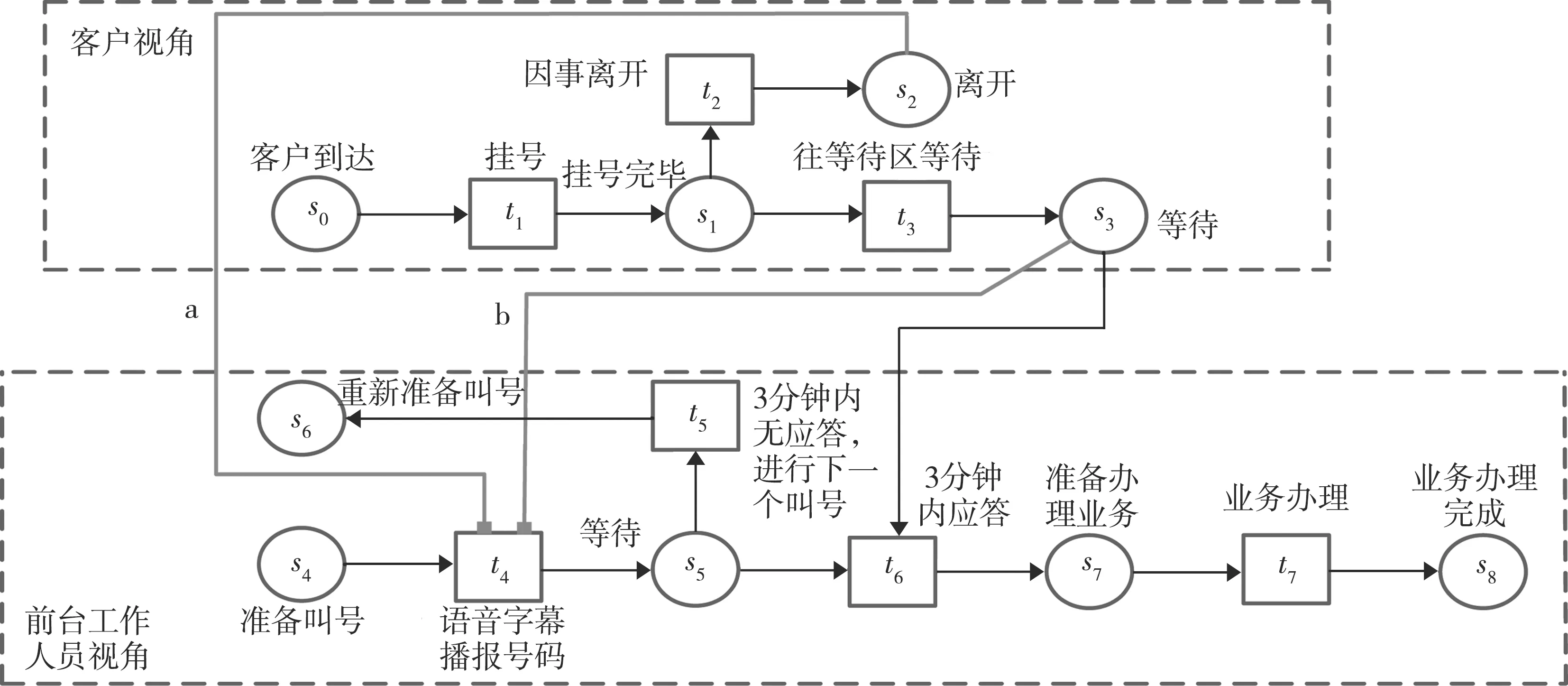
图4 前台办理业务的流程模型

客户到达时，变迁t1发生。客户挂号完毕，引发t2或t3(两者为排他关系)。t2或t3的发生，导致客户有不同的状态s2或s5。

前台工作人员叫号时，变迁t4发生。叫号完毕时，到达状态s5，进入等待状态，引发t5或t6(两者是排他关系)。t6的发生权由s3和s5决定，若客户已离开，则s3中无Token，此时t6无发生权。若客户因为紧急事件离开且3 min内无应答而造成该号废弃，即t5发生，则前台重新叫号，到达s6，此次业务办理流程结束；若t6发生，即客户3 min内应答，则引发t7(业务办理)，随后到达s8。

2.2 流程模型优化

由上述描述可知，若客户离开了，工作人员必须等待3 min才能进行下一个叫号，其他客户也会多等待3 min时间。若这种情况频繁发生，将严重影响客户的体验和前台工作人员的工作效率。为防止这种情况频繁发生，则需要对客户的行为进行一定的约束。可引入挂号取消系统、信息系统、挂号分类和信誉制度，增强客户状态与前台工作人员之间的交互，约束客户的个人行为，从而提高工作效率。

(1) 信息系统。客户挂号一般是通过使用身份证+手机号(或其中之一)的方式进行，因此可通过信息系统记录客户的行为，并根据客户行为对客户的信誉等级进行评价。

2）轻理论，重实践。在意识到上述缺陷之后，很多学者提出培养无缝对接的职业人才，要培养一批出来就直接可以使用的一线人员。在这个思路下，很多院校把学生的实习实训时间大幅度提高，由于学生总的课时是一定的，只能大幅度压缩理论学习时间。这样培养的学生虽然具备很强的动手能力，到了公司可以立马上手，但是由于缺乏一定的理论基础，对后续发展造成很大损害。

(2) 挂号取消系统。客户在挂号后由于各种原因而无法继续等待，则可以通过挂号取消系统取消挂号。前台业务人员可以通过查询信息系统来获知客户是否取消挂号。

(3) 挂号分类。对客户的信誉等级，在后续挂号服务中系统自动进行判别。将信誉等级正常的客户挂号归入A类，将信誉等级较低的客户挂号归入B类。

(4) 信誉制度。信息系统对客户的行为进行记录，并进行信誉分级。比如规定：a.若某客户1个月内3次未取消挂号而离开，则评价其信誉等级较低。后续服务中，前台叫号后的等待时间降低为30 s；b.若某客户1个月内超过5次未取消挂号而离开，则将其拉入“黑名单”，原则上后续半年内对其不提供挂号服务。

基于以上思路，优化后的流程模型如图5所示。表1和表2为相应的库所和变迁的定义。

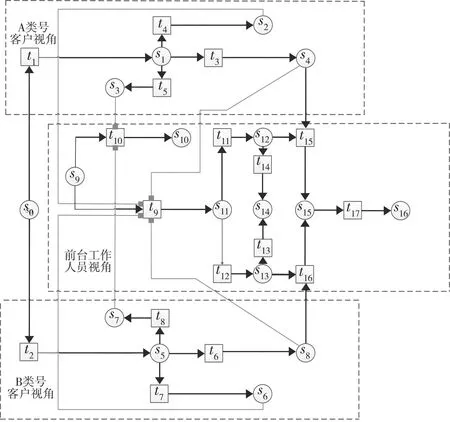
图5 优化后的前台办理业务流程模型

在客户挂号时，系统依据其信誉等级对其进行区分，信誉正常的为A类号，信誉等级较低的为B类号(通过t1和t2实现)。在挂号完成后增设挂号取消系统，通过t5和t8实现。客户如遇紧急情况而无法继续等待办理，可以通过取消挂号系统取消挂号，这时s3或s7中会产生一个Token，激发t0发生，到达s10，此次业务流程结束。

前台工作人员在播报号码前，要查看该号客户是否取消挂号。若客户已取消挂号，则发生t10，此次业务流程结束；若未取消挂号，则发生t9，并引发t11或t12，播报号码和告知等待时间。接着，客户到达s12或s13，工作人员等待顾客应答。若客户未应答，则发生t13或t14，此次业务流程结束，信息系统记录该客户行为；若客户在规定时间内应答，则发生t15或t16，到达t15，准备办理业务。

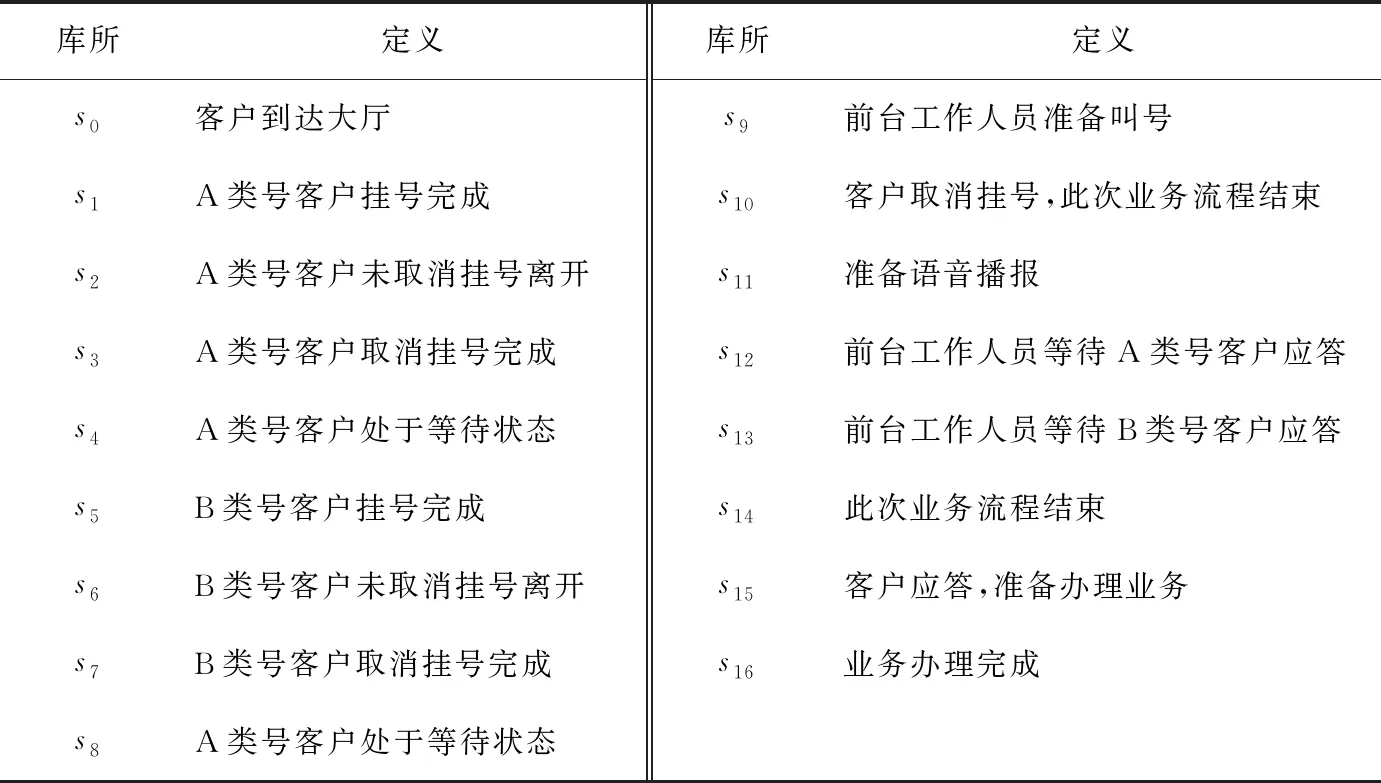
表1 库所定义

表2 变迁定义

3 仿真实验及效果分析

为了检验优化后的流程模型的正确性和可行性，使用PIPE工具构建优化后的Petri网模型，进行了仿真实验。通过状态空间分析，得到的结果证明，该模型是有界的、安全的、无死锁的，是合理且可行的。

下面，通过计算某个窗口某一时段客户挂号后额外等待的时间(即该时段内前台工作人员业务停滞的时间)，比较优化前后模型的执行效果。

假设在一定时段内，前台的某个服务窗口共有50名客户等待办理业务，其中有40名客户为正常办理业务的客户，有10名客户会因紧急事件而离开。正常办理业务的客户在应答过程中造成的额外等待时间为每人15 s(即0.25 min)。在优化前的模型中，由于不存在取消挂号系统等规定的约束，前台工作人员将因为每个直接离开的客户而使业务都停滞3 min。因此，在这个时段某窗口的业务停滞时间合计为：0.25×40+3×10=40(min)。在优化后的模型中，由于有信息系统、取消挂号系统和信誉制度的存在和约束，客户的分类和挂号后的行为也有所不同。假定其中正常办理业务的客户同样为40名，而完成取消挂号的客户为5名，未完成取消挂号而直接离开的A类客户为2名、B类客户为3名。导致的额外等待时间是：正常办理业务的客户每人为0.25 min，完成取消挂号的客户每人为0 min，直接离开的A类客户每人为3 min，直接离开的B类客户每人为0.5 min。由此计算，得该窗口的业务停滞时间合计为：0.25×40+0×5+3×2+0.5×3=17.5(min)。在50名客户中仍然有10名客户放弃办理业务，且其中有2名A类客户(占4%)和3名B类客户(占6%)直接离开的情况下，按优化后的模型执行，这个时段内该窗口的业务停滞时间，也将比执行优化前的模型而减少22.5 min。也就是说，在此时段内，窗口业务停滞时间可减少56%。

4 结 语

鉴于挂号排队的前台业务流程中存在的问题，为减少服务窗口闲置与客户等待时间，我们基于Petri网行为轮廓与可达性，对前台办理业务的流程进行了建模分析。然后针对客户的个人行为，引入信息系统、挂号取消系统和信誉制度等对客户的行为进行约束，通过增加相关的结构变迁和库所对流程模型进行了优化。仿真实验和测试结果表明，优化后的流程模型是有界且安全的；按优化的流程模型执行，可以大幅度减少服务窗口的闲置时间和客户额外等待的时间。