注水油田高含水期流场重构模型研究与应用
张 静 刘玉娟 刘 东 刘 斌 瞿朝朝
(中海石油(中国)有限公司天津分公司, 天津 300459)
对于海上油田来说,由于工程及成本原因,在高含水阶段实施加密调整等提高采收率方法比较困难;同时受注水、注聚长期影响,地下流场变得更加复杂,层内、层间及平面非均质性突出,油田形成固有流场[1-3],按常规方法注水往往难以满足高含水期油田开发生产的需要。因此,需要研究油藏高含水期的流场重构方法,提高注水波及系数,从而提高储量动用程度。油田进入高含水期后,进行流场重构的方法主要有周期注水法、基于油水井动态分析的经验法、注采井网调整、调剖调驱等[4-8]。但是,这些方法都很难根据注水效果、流场分布区域来定量调整单井注水量。
本次研究,基于流线数值模拟模型[9-11],定量分析各小层油水井间的流线分布、注采分配因子、平均含水率及驱油效率[12],以改变注水量调整压力平衡点为手段,以提升驱油效率为目标,建立单井注水量优化模型,进行不同流场下的单井注水量调整计算,探索了一种流场重构方法,提高油田开发效果。
1 原理及思路
通过改变注水井注入量,可以使压力平衡点移动,以此引导弱流线、构建新流线,重构流场。图1a为同等强度注入条件下的压力等值线图,图1b为不同强度注入条件下的压力等值线图。由此可以看出,注水井I1、I3、I5井在注入强度变化之后,压力平衡点发生了移动,流线不再沿固定位置分布,其方向发生了偏转,原来流线较弱的区域被有效波及。同时,注采强度降低的注水井I2、I4井附近,形成了新的弱波及区。当I2、I4井改变注入强度后,流线将会再次发生偏转,构建出新流线,扩大波及,同时降低含油饱和度,提升驱油效率。

图1 不同注入强度下的压力等值线图
按照通过改变注水井注入量使压力平衡点移动而重构流场的思路,建立单井注水量调整模型。计算流程如图2所示。
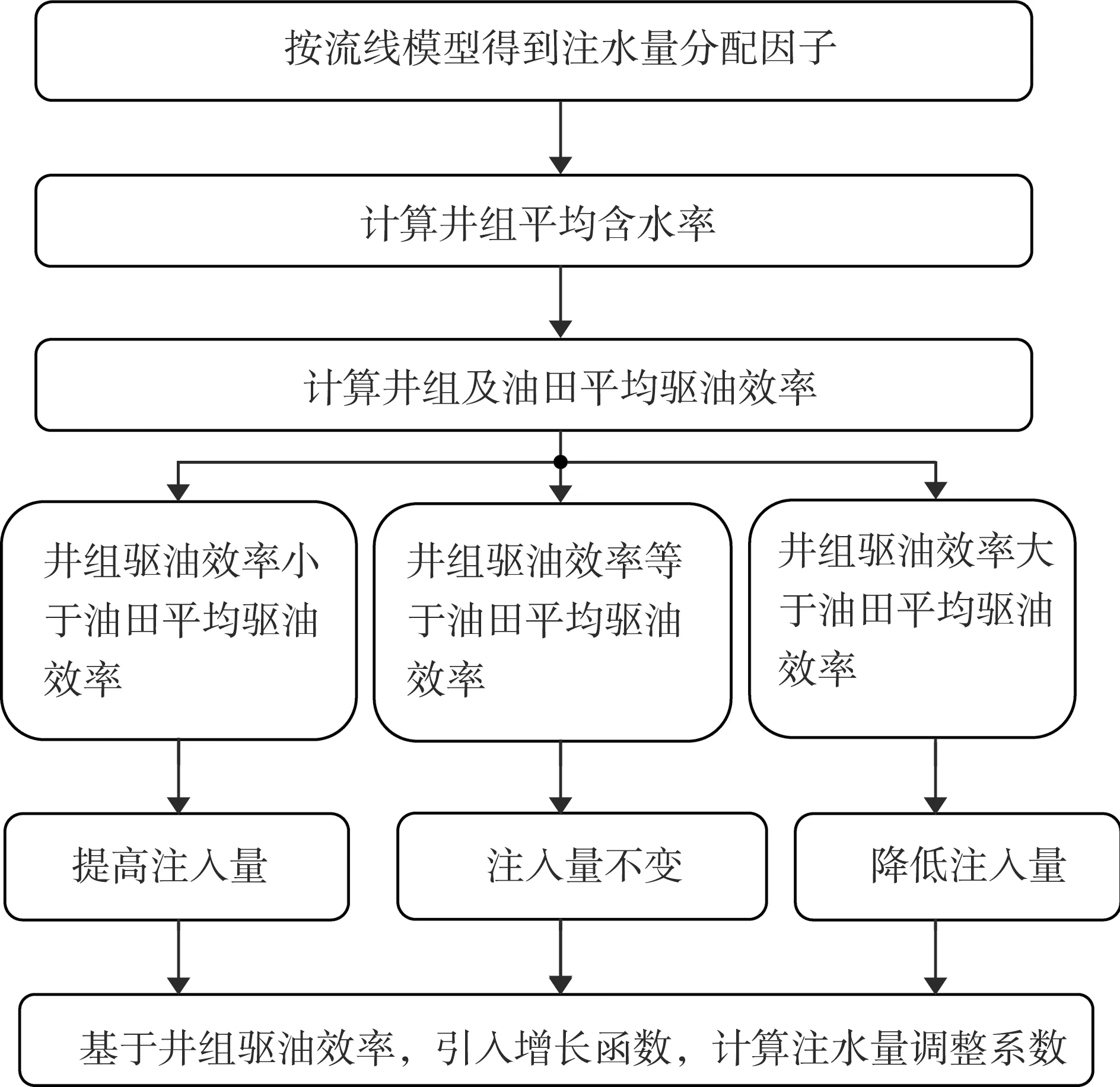
图2 注水油田高含水期流场重构模型计算流程
2 流场重构优化模型研究
2.1 模型的建立
以一个注采井组为计算单元。假设条件为:该井组多层合采;各小层相对渗透率曲线相同;忽略毛管力及重力。
2.1.1 井组平均含水率
根据流线模拟结果,可以得到当前生产状况下的各油水井间的流线分布及以注采分配因子为表征的注采井流量分配关系[13]。注采井组的平均含水率fw用式(1)计算。
(1)
式中:Qwi—— 受注水井i有效驱替的所有相关油井的日总产水量,m3d;
QLi—— 受注水井i有效驱替的所有相关油井的日总产液量,m3d;
dwj—— 油井j的产水量对注水井i的分配因子,无因次;
doj—— 油井j的产油量对注水井i的分配因子,无因次;
n—— 与注水井i有对应关系的油井数;
qwj—— 油井j的单井日产水量,m3d;
qoj—— 油井j的单井日产油量,m3d。
2.1.2 井组驱油效率
引入相渗表达式和分流量方程,联立可得含水率方程。统计渤海注水油田相渗数据,可知油水指数no与nw的值为2~3。针对渤海S油田C区井组,将油相指数no与水相指数nw的取值均设定为2。
相渗表达式:
(2)
(3)
式中:Kro—— 油相相对渗透率,无量纲;
Krw—— 水相相对渗透率,无量纲;
Sor—— 残余油饱和度;
Swc—— 束缚水饱和度;
Sw—— 出口端含水饱和度。
分流量方程:
(4)
式中:fw—— 井组平均含水率;
μo—— 油相黏度,mPa·s;
μw——水相黏度,mPa·s。
含水率方程:
fw=1{1+[(1-Sw-Sor)(1-Swc-Sor)]2
[(Sw-Swc)(1-Swc-Sor)]2×
(μwμo)}
(5)
于是,可得出口端含水饱和度:
(6)
井组平均含水饱和度:
(7)
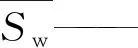
fw′ —— 含水上升率。
井组驱油效率:
(8)
式中:Ed—— 井组驱油效率。
将式(6)(7)代入式(8),得:
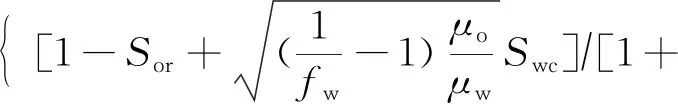
(9)
2.1.3 注水量调整系数
以驱油效率为调整目标,可以针对性地抑制无效水循环,更有效地提升驱油效率低的水井的驱油效果。
以井组驱油效率为变量,基于试凑法理念,以一个变量α控制和约束增长速度,引入增长函数模型如式(10)和式(11)所示,进行注水量优化计算。
(10)
(11)
式中:fi—— 注水量调整系数;
α—— 增长函数底数,约束fi的大小,α≥10;
Edi——i井组的驱油效率;
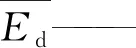
Ed max—— 油田注水井组的最大驱油效率;
Ed min—— 油田注水井组的最小驱油效率。
当井组驱油效率与油田平均驱油效率一致时,则注水量调整系数fi=0。
当井组驱油效率高于油田平均驱油效率时,用式(10)计算。注水量调整系数fi>0,且其绝对值随着井组驱油效率的提高而增大。
当井组驱油效率低于油田平均驱油效率时,用式(11)计算。注水量调整系数fi<0,且其绝对值随着井组驱油效率的提高而减小。
2.1.4 注水井注水量
注水井的注水量调整,按式(12)计算。为了保证注采平衡,使优化调整前后总注水量一致,定义注采平衡约束系数b为优化调整前区块总注水量与调整后区块总注水量的比值[9]。因此,优化调整后的注水量按式(13)计算。
qxi= (1-fi)qyi
(12)
qti=qxib
(13)
式中:qxi—— 调整后注水量,m3d;
qyi—— 调整前注水量,m3d;
qti—— 注采平衡后最终新注水量,m3d;
b—— 注采平衡约束系数。
2.2 模型的求解
流场重构模型主要求取的是注水量调整系数。求取注水量调整系数,关键在于增长函数的底数α,是通过α来约束注水量调整系数随井组驱油效率的增长速度。
针对选取的不同底数,绘制注水量调整系数曲线,以驱油效率为横坐标,注水量调整系数为纵坐标,如图3所示。可以看出,当底数α处于10到50之间时,注水量调整系数fi绝对值最大值逐渐从1变为0.5,即注水量最大调整幅度为50%~100%;α大于50以后,即使再增大至200,在相同的井组驱油效率下,α对应的注水量调整系数fi的变化不大,且最大注水量调整幅度控制在50%以内。
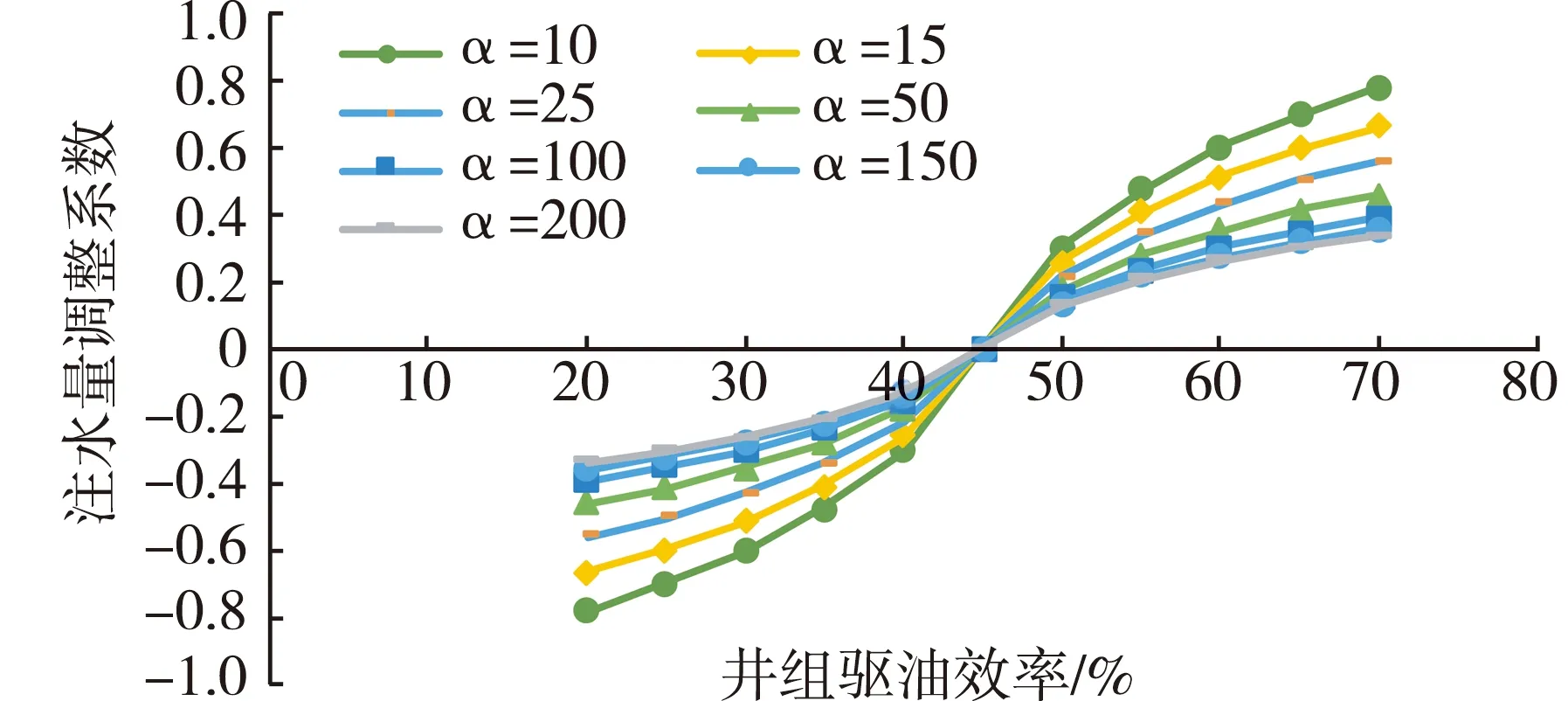
图3 不同优化模型下的注水量调整系数变化曲线
最终选取α=50,对注水量调整系数进行计算。在注水井组驱油效率接近油田平均驱油效率时,对其注水量进行微调。当注水井组驱油效率严重偏离油田平均驱油效率时,对其注水量进行较大幅度的调整[4]。在α=50时,注水量调整系数为-0.5~+0.5,即注水量调整幅度不大于原注水量的50%,基本处于矿场实际注水井注水能力限制范围内。
2.3 敏感因素分析
以渤海S油田井组为算例,对注水量增长函数优化模型进行敏感因素分析。油田平均驱油效率为45.1%,增长函数中底数α与注水量调整系数fi的关系如图4所示。
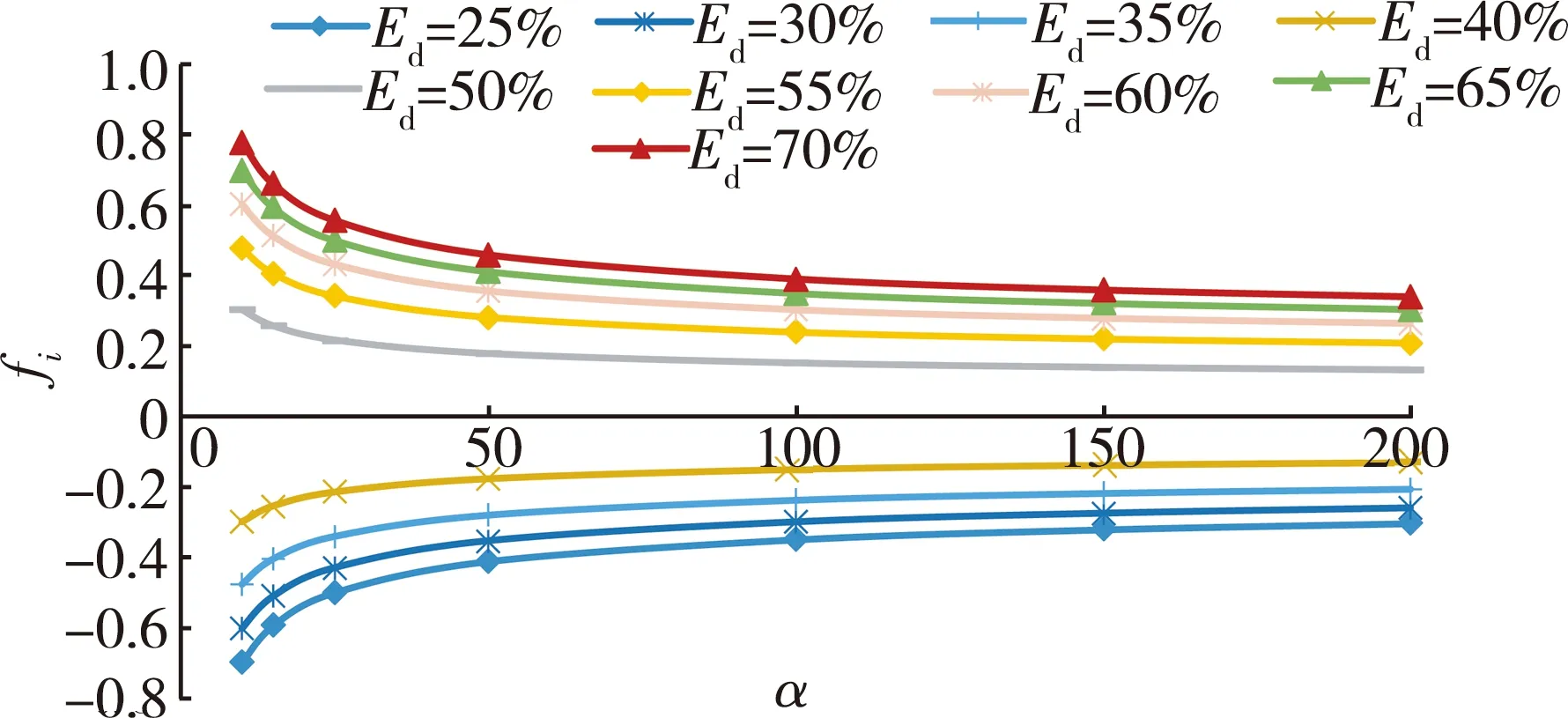
图4 不同驱油效率下优化模型α与fi的关系曲线
从图4可以看出:(1) 井组驱油效率越接近油田平均驱油效率时,注水量调整系数越小;井组驱油效率偏离油田平均驱油效率越远,注水量调整系数越大。(2) 井组驱油效率高于油田平均驱油效率时,注水量调整系数为正,且随着优化模型底数的增大,注水量调整系数逐渐变小。(3) 井组驱油效率低于油田平均驱油效率时,注水量调整系数为负,随着优化模型底数的增大,注水量调整系数逐渐变大。(4) 当优化模型底数大于50时,注水量调整系数曲线整体出现拐点,变化趋于平缓。
3 矿场应用效果分析
渤海S油田位于渤海辽东湾海域,属于高孔高渗储层。其主力含油层段为东营组东二下段,纵向上分为4个油组,原油密度大、黏度高,属稠油油田。开发初期布署反九点井网,后逐步调整为行列井网。
通过数值模拟流线模型,得到当前生产状况下的各油水井间的流线分布、以注采分配因子为表征的注采井流量分配关系。通过分析计算,得到油田目前的平均驱油效率为45.1%。按照增长函数优化数模型进行单井注水量调整系数优化。根据注采平衡要求,优化调整前后总注水量应一致。注水量调整前为946 m3d,调整后为889 m3d。根据注采平衡约束系数,得到最终注水量调整结果(见表1)。
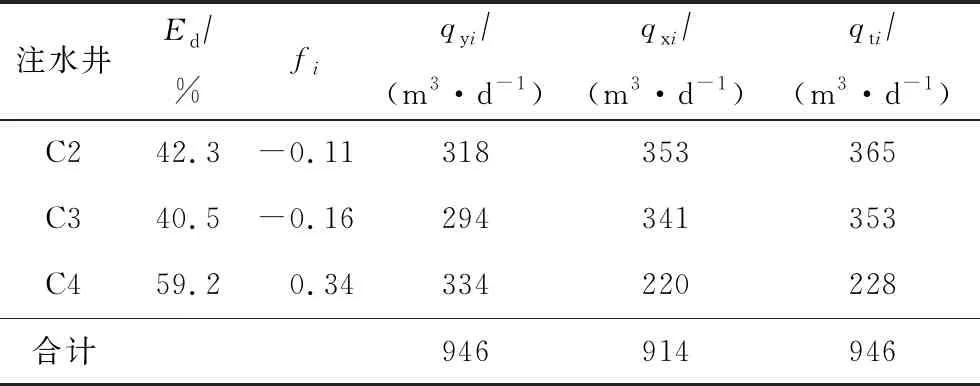
表1 注水量调整结果
优化前,注水井C2、C3、C4的注水量分别为318、294、334 m3d。优化后,这3口井的注水量分别为365、353、228 m3d。2018年5月,C2、C3、C4井组现场实施了新方法的优化注水试验。对比优化前后的流线分布情况,可明显看出,优化后的流线分布更加均匀(见图5),增油效果明显(见图6),井组含水比实施前下降6.0%,井组增油50 m3d。截至2019年5月,井组累计增油1.0×104m3,显示了流场重构效果。
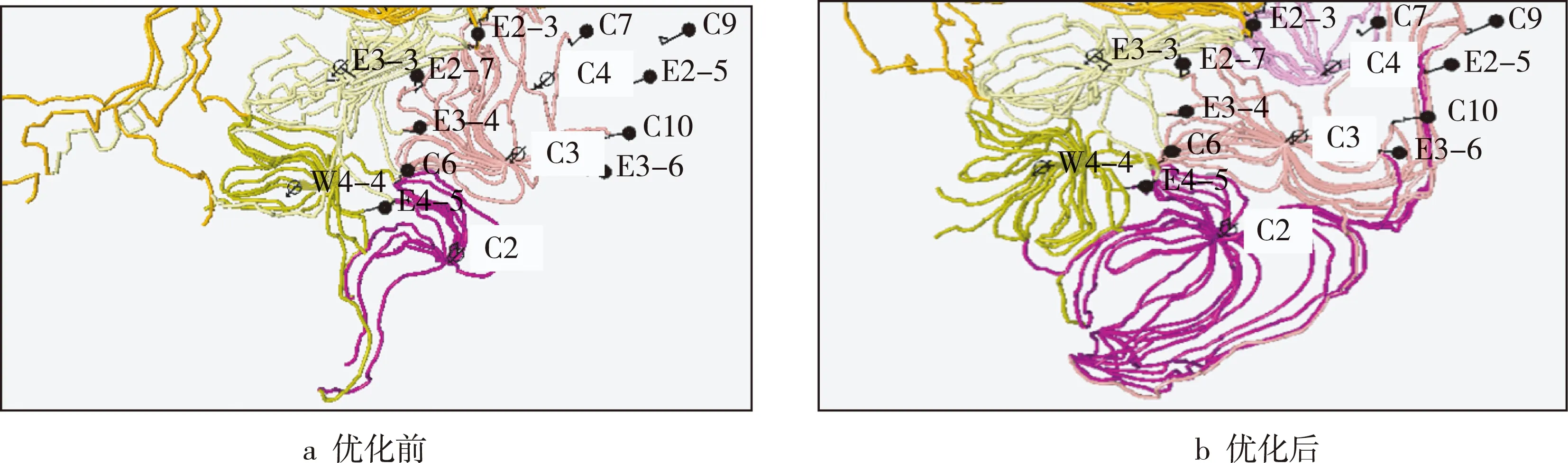
图5 优化前后流线模型中的流线分布
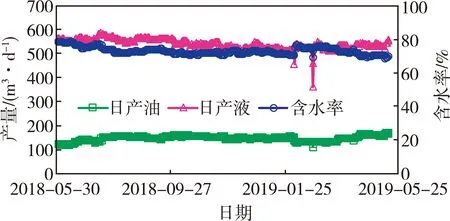
图6 渤海S油田C2、C3、C4井组生产曲线图
4 结 语
以提升井组驱油效率为目标,基于流线分布及注采分配因子,建立了单井注水量增长函数优化模型。油田井组平均驱油效率越接近于油田平均驱油效率时,注水量调整幅度越小;井组平均驱油效率偏离油田平均驱油效率越远,注水量调整幅度越大。矿场应用效果表明,根据该模型进行注水调整是有效的。海上大段防砂且处于中高含水期的油田,通过优化调整,可以扩大水驱波及范围,改善注水开发效果。

