说理：让数学学习从“长知识”走向“有价值”*——人教版六上《负数》一课的教学思考

罗鸣亮

【背景】

负数的认识是数概念的一次扩充，标志着数学发展的又一次飞跃。以往学习的自然数（0 除外）、分数、小数等正数都是度量产生的结果，其核心是计数单位，其中，自然数和小数还凸显十进位值制这一关键。负数的扩充已不再那么自然，它不是测量所得的结果，其根本属性是表示与正数相反意义的量。所以，对于学生来说，与以往所学的数相比，负数的学习较为抽象、困难。

人教版、北师大版、苏教版小学数学教材主要从以下两个方面帮助学生理解和认识负数：一是基于现实需要研究负数的现实模型，认识负数；二是结合实例，从丰富的现实背景中理解负数表示的是与正数相反意义的量。但数学学习不能仅仅停留在对现实生活的应用上，还应从数学及学生内部发展的需要来思考，体现数学这门学科独有的培养人的数学思维的价值。

如果只是把书本上的知识搬到课堂上，还不能称其为“学习”。知识本身都蕴含着一定的要求与价值期待，只有在具有挑战性的真实问题驱动下，才能使学生真正思考起来，变被动的输入学习为主动的输出建构，从而实现从纯粹的知识获取到有价值的知识体悟的转变，这便是“说理课堂”追寻的模样。如在教学负数时，教师透过问题这一杠杆支点，立足学生的现实生活和数学发展的内在需求，推动学生真正理解负数的数学本质，体会负数产生的原因、过程及其意义。在此过程中，不断放大负数的价值，促使学生用理性的思维方式，整合自身及他人的观点，汇集集体的力量来解决问题。同时，引导学生超越原有的知识属性与规定，在直接的、有用的、多层次的学习中追溯负数产生的源头，推动他们一次次打开未知的世界，开放思维，真正进入负数这一知识所承载的深远意义，最终不仅使学生获得了知识，更使他们看到了知识的价值。

【教学过程及分析】

一、明——理清起点

师：大家见过负数吗？生：见过。

师：都见过啦，会写吗？写一写。你们可以边写边读给同桌听。

教师随机请一个学生到黑板上读写负数。

生（边写边读）：-1，-2，-3。（全班齐读黑板上书写的负数）

师：你在教大家读，是吧？你再写一个，看看大家还会不会读了。

全班（齐读）：负七分之四。

负数虽为新知，但学生对它并非一无所知。在现实生活中，学生都见过负数，知道它在生活中表示的意义，甚至能自己把它从生活中抽象出来，有一定的数学认识，会读写负数。但真正的学习不只是表面叙述和理解知识的属性，教师应该帮助学生有层次地探究知识的多维属性和深远意义。课堂伊始，教师通过与学生对话拉开负数学习的序幕，看似简单，实则是为了深入到学生的实际认识中，准确把握、立足学生已有的认知基础，洞悉学生有关负数认知的最大区域，了解学生的真正需求，发现学生的真实困惑，找到学生的现有水平和将要去往的未来水平之间的联结点，从而确立学习的生长点，使学生于不知不觉中进入真正的学习状态，以期使负数从纯粹的知识转变成有价值的知识。

二、思——理向本源

话题一：假如世界上没有负数，可以吗？请说明理由。

四人小组热烈讨论，之后组织学生汇报讨论的结果。

生1：这世界上不可能没有负数。如“1-2”，2 比1 大，如果没有负数，就算不出“1-2”的差了，所以得有一个负数来表示它们俩的差。

生2：我觉得不可以，因为如果没有负数的话，低于零度的温度、低于海平面的海拔该怎么来表示呢？

每个学生的发言都引来一阵掌声。

师：很奇怪，我听到的都是掌声。竟然没有一个人去反驳他们的观点。

生3：我觉得低于零度的温度，也可以直接写成零下几度，所以没有负数也可以。

生4：负数可以省略一些字，直接加条杠就可以把文字代替掉了，所以不可以没有负数。

师：我们以前不是学过很多数吗？为什么不够用了呢？

生5：因为在我们学过的数里，表示的都是有多少数，没有一个数可以表示缺了多少数。

生6：而且我们以前学的数没有一个是低于0的数，小于0的数。

师：对呀，就像你们说的，生活中有地上有地下，有多的有缺的，为了表示这样两种相反意义的量，我们就把原来认识的数都称为正数，这时候另外一种就要用什么来表示呀？

生：负数。

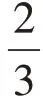
生：需要。

对于学生来说，知道知识在哪儿，又缘何产生，比知道这个知识是什么更为重要。真正触发学生学习的不是他们已有的认知存量，而是他们在求知路上遇到的问题。为什么要学习负数？负数究竟是怎么产生的？这是大多数学生的认知困惑点，它们恰恰能帮助学生反求诸己，重新审视自我。上述教学，借助话题一引发学生调用已有的经验与认知，观察、思考、辨析、理解平时没有关注到的问题，使他们主动在生活与数学之间以及各个数学知识之间建立起链接，在抽象中借助自身的经验，倾听他人的思考，通过不断还原追溯到负数产生的源头深处，从而促进他们既从自然背景和人为规定等生活实例中感悟负数产生的意义，又从数学减法的视角体会负数比0还小，进而思考引入负数的必要性。

三、辩——理向未知

话题二：0是正数还是负数呢？请说明理由。

四人小组热烈讨论，之后组织学生汇报讨论的结果。

生1：我觉得0 既不是正数也不是负数，因为它不缺少什么，也不增加什么。

生2：0 表示的是没有，正数表示的是增加了多少，负数表示的是减少了多少，而且0 前面加一个负号和0前面不加负号是一样的，所以0既不是正数也不是负数。

生3：如果0 是正数的话，表示得0 个，等于没有；如果它是负数的话，表示缺0 个，说明没有缺，所以我觉得0是个独特的数。

师：那么，0 到底是什么呢？我们来做一件事。（出示图1）请你把珠穆朗玛峰和吐鲁番盆地的海拔高度与同桌说一说。再想一想，为什么吐鲁番盆地的海拔高度可以用负数来表示？

生4：因为它低于海平面，也是小于0。

生5：这时候的0表示海平面。它是一个中间数，也是一个分界线。

师：如果以这个为分界线（指着大屏幕上海平面以下的位置），吐鲁番盆地的海拔还是负数吗？可见0 不只是一个分界线，还表示一个标准数。再看，（出示图2）这时候的0摄氏度是有度数还是没有度数？

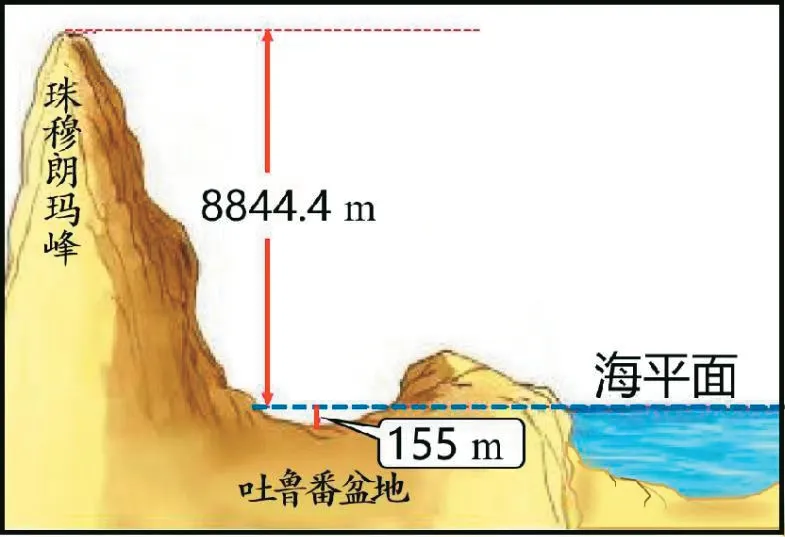
（图1）

（图2）

生：有度数。

师：对了，0 不仅仅是一个分界线，是一个标准，还能表示实际意义。

“已知”有时会成为阻碍新发现的重大障碍，但有时又是启发新思考的关键要素，关键在于能否透过“已知”看到“未知”。对学生来说，0既熟悉又陌生。学生已经知道0 作为自然数表示没有。话题二紧扣学生的困惑点、生长点，启发学生跳出眼前的问题，帮助他们突破原有对0 的认知，从正数、负数这一组表示相反意义的量出发开启逆向思考，经由正数和负数的认知链接起对0 的新认识，从而带动知识链的建构和碰撞，重新定义0 的价值。之后，教师以“海拔高度”和“温度”为例，引导学生体会0 可以表示分界线，同时又是区分正负数的标准，感受0还可以表示海平面的高度、一个具体的温度等确定的量，具有实际意义，促进学生将对正数和负数的认识向纵深推进。

四、推——理向开放

话题三：他们说的是真的吗？请说明理由。

1.出示图3：图中说的是真的吗？请说明理由。

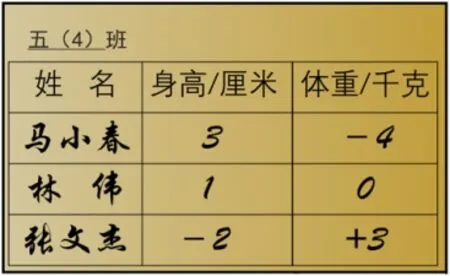
（图3）

生1：我觉得不是真的，因为人不可能往下长，只能往上长。长到-2厘米是不可能的。

生2：我觉得应该是真的，因为这里的3 也许可以表示其他的数，还有1，还有-2。

生3：我觉得是对的。如果及格线是140厘米，张文杰是138厘米，是有-2这个身高的。

大家恍然大悟，教室里不由得响起阵阵掌声。

2.出示图4：张文杰说的是真的吗？

生1：我觉得他说的有可能是真的。它上面只画了竖着走两格，有可能他家是横着走两格。用数对（3，1）表示。

揭示：数对（3，1）是少年宫。

生2：我觉得张文杰说的是真的，他可以从学校往下面走，走两格的话，图上没有表示出来，但可以用负数表示，因为0 是这张图的底线，但实际上0不一定是底线。

（图4）

师（出示图5）：以前我们对数轴的认识只限定在正数范围内，现在有了负数，张文杰的家可以向四面八方延展了。

（图5）

判断学习是否真正发生，就要看学生能否活学活用，能否主动运用学到的知识来解决问题，并从中“悟道”，充分展现知识的价值。话题三引发学生借用前面的学习照耀新的思维空间，启发学生通过自己的思考再次深刻理解0的价值，内化正数和负数是表示相反意义的量的数学本质，帮助学生感知用正数、负数描述和记录生活世界的合理性、严谨性和系统性，使他们进一步体验用正数、负数刻画生活世界的独特魅力和实用价值。

好的问题是与学生的生活实际和认知实际相关联的、具有挑战性的问题。它就像学习的杠杆支点一样，能撬动学生的好奇心，引发他们追寻学习的真理；能撬动学生的生活经验和已有认知，引领他们往未知领域前行；能撬动学生的思维，促进他们向更开放、更自由的学习深处奔跑；更能撬动学生主动立在课堂中央的欲望，激发他们自由地表达、畅快地思考、深入地交流。本课的教学，旨在促进学生借助符号知识认识、理解、把握负数所承载的价值和意义，推动学生在追溯、辨析、说理的过程中不断反思自我、更新认知、创造学习。在丰富知识的意义和价值的同时，引导学生理解和建构起自己对客观世界的认知方式，这正是说理课堂的根本追求。