再入攻角对弹头锥身气动热环境及结构热响应影响研究
(中国工程物理研究院总体工程研究所,四川 绵阳 621999)
再入环境测量火箭试验平台可同步获取再入自由飞行状态下弹头(脉动)压力、温度、过载等再入力热环境数据及振动、噪声等结构响应数据,为再入飞行环境特性研究提供有效数据[1-3]。为避免弹头壁面烧蚀对测试结果的影响,并为壁面测试传感器选型提供前提条件,应开展弹头锥身测试舱壳体再入气动热效应研究,分析防热设计可行性,为非烧蚀防热飞行器的热环境准确预测提供参考[4-6]。
飞行攻角是影响火箭测试平台测试舱再入气动热环境及结构热响应的重要参数之一。随着攻角的增大,迎风面气动加热增强,表面及结构温度也将随之升高[7-8]。与传统火箭弹弹头普通以零攻再入飞行,无需考虑攻角对气动热效应影响不同,再入环境测量火箭试验平台为了满足飞行测试需求,其弹头再入飞行攻角呈振荡收敛的变化过程。因此,攻角效应是火箭测试平台防热设计时需特殊考虑的影响因素。
大量学者开展了基于工程法或数值法的气动热/结构热耦合计算方法研究,并开展了典型飞行器典型结构气动热响应特性研究[9-20],分析了再入攻角、滚转运动等对结构热响应的影响。如陈自发等[20]获得了固定攻角时弹头的烧蚀外形,研究了飞行攻角对烧蚀特性的影响。
目前的研究重点关注固定飞行攻角条件下气动热/结构耦合问题的研究[8-20]。对于实际飞行过程飞行器热环境及结构热响应的准确预测,需开展变攻角飞行条件下的气动热、结构耦合分析。该方面的研究较少,对其影响规律认识仍显不足。
文中采用基于工程法的气动热/结构热响应耦合计算方法,针对某火箭测试平台弹头锥身壳体结构,研究了再入飞行攻角振荡对再入热环境及壳体结构热响应特性的影响规律。该研究可为该类飞行器防热设计、热环境准确预测提供参考。
1 飞行弹道及锥身防隔热方案
1.1 弹道特性
文中计算时采用的弹道为理想条件下的惯性弹道,其速度曲线如图1 所示。飞行过程中,主动段飞行攻角为0。全弹主动段结束时的速度最大,约为1700 m/s。再入时,飞行攻角呈振荡衰减变化规律,最大飞行速度为1355.6 m/s。
1.2 弹头锥身防隔热方案
在火箭测试平台方案设计阶段,以零攻再入飞行条件为前提条件开展了锥身壳体防隔热方案设计。为了保持再入弹头气动外形不变,弹头需要进行非烧蚀设计,无法采用壳体外壁面喷涂涂层的防热方法。结合测试传感器安装及使用要求,采用壳体自身热沉降低结构温度的防热方案。综合考虑质量特性要求及加工要求,经防热材料选型、壳体厚度优化设计,壳体采用20 mm 厚度合金钢材料。

图1 速度曲线Fig.1 The flying velocity
针对再入过程中锥身壳体温度短时间超过100 ℃,无法满足弹头内部温度要求的问题,采用壳体内壁面增加隔热材料及高反射率材料的方式进行改善。经设计,内壁面增加2 mm 厚度的低导热泡沫材料作为隔热层,降低壳体内壁面温升。
在以上弹头锥身壳体防隔热方案基础上,开展了再入攻角振荡对再入热环境及壳体结构热响应影响研究。该平台弹头采用球单锥外形。研究位置为距弹头顶点轴向x=0.6 m 锥身处。
2 计算模型
对于再入飞行器气动热环境的计算方法可分为工程法和数值法。其中,数值法计算成本高、周期长,适用于复杂外形气动热环境计算。工程法计算成本低、效率高,对于球锥、弹翼等外形具有非常好的适用性。
针对文中的计算模型,采用了基于工程法的气动热环境计算方法,并与固体热传导方程耦合求解壳体结构温度。气动热/结构热响应耦合计算流程如图2所示。其中,大气参数模块读入弹头的弹道飞行参数(速度、高度等),并计算出来流参数(来流密度、温度等),以用于对流热流密度计算。根据飞行攻角、飞行器外形参数(半锥角)计算等价锥角,用于热流密度计算。根据结构温度,材料参数模块计算结构材料热力学参数,用于结构热传导求解。
在防热结构温度场计算时,以热流密度作为外壁面边界条件,内边界条件采用绝热壁面边界条件。其中,防热结构外壁面温度计算时,考虑了对流传热及辐射散热的影响。在壁面热流计算过程中,流动状态对热流密度有重要影响,对于不同流动状态下的热流密度采用不同的计算方法。其中,转捩判据采用广泛使用的72-90 准则。

图2 气动热/结构热响应耦合计算流程Fig.2 The flow chart of the coupling calculation method
层流状态下,采用Lees 计算方法开展壁面热流密度计算,见式(1):

湍流状态下,本文采用平板参考焓方法开展壁面热流密度计算。球锥外形湍流区的热流密度计算公式见式(2):
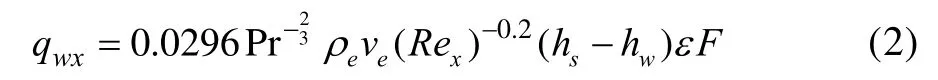
式中:ε为压缩因子;F为形状因子。
参考焓方法是计算高速边界层非驻点传热的一种普遍使用的半经验公式。文中采用的Eckert 参考焓方程为:
3 计算结果与分析
3.1 零攻再入时气动热环境及结构热响应特性
零攻再入时,弹头锥身热流密度及焓值随飞行时间的变化曲线如图3 所示。飞行过程中,焓值随飞行时间呈双峰形态,分别出现在主动段关机点时刻附近及再入22 km 高度处,最大值分别为1.55、1.08 MJ/kg。
零攻再入时,锥身截面热流密度随飞行时间呈出双峰形态,分别出现在主动段关机点时刻附近及落地时刻附近,最大值分别为1.6、0.84 MW/m2。由于飞行高度较高,速度较小,测试舱壁面热流密度在50~280 s 时基本为0。上升段、再入段时的加热量分别占飞行过程中总加热量的52%、48%,两者相当。总体而言,测试舱再入热环境为低热流、低焓环境。
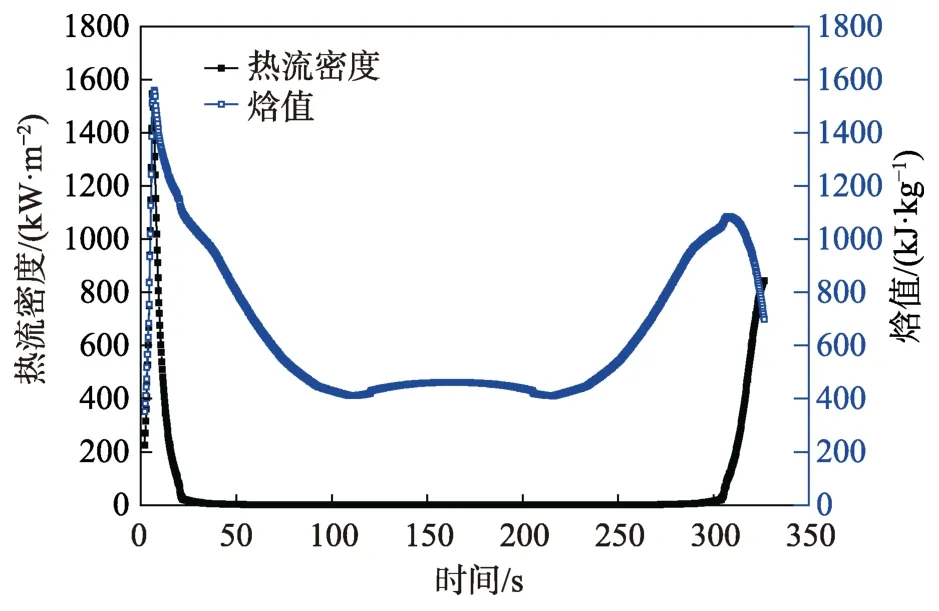
图3 锥身截面热流密度及焓值随时间历程曲线Fig.3 The aerodynamic heating environment parameters
锥身截面典型位置处的结构温度曲线如图4 所示。其中,金属层内壁面为防热层与隔热层接触面,其温度也代表了隔热层外壁面温度。在气动加热作用下,金属层外壁面温度随时间的变化规律与热流密度相似。由于结构的热沉作用,虽然再入时的最大热流密度小于上升段,但落地时刻外壁面温度最高,为481 K。
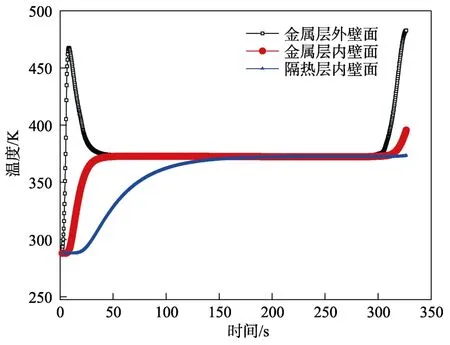
图4 典型位置处结构温度曲线Fig.4 The structure temperature curve in typical position
隔热层内外壁面温度随时间的变化规律相同,均表现出先增大、后保持不变、再增大的变化规律。由于隔热层的隔热作用,隔热层内壁面温度变化显著滞后。落地时刻内壁面最大温升为85 K,与再入前相比,基本保持不变。
3.2 非零攻再入时气动热环境及结构热响应特性
为了满足测试要求,测试平台高空再入时具有一定的初始攻角,从而对锥身再入热环境及结构热响应特性产生影响。根据该火箭测试平台再入热流密度变化规律,文中主要研究25 km 飞行高度以下时再入飞行攻角对锥身气动热环境及结构热响应的影响规律。
不同振荡频率下再入攻角随飞行时间的变化曲线如图5 所示。再入时,飞行攻角随时间呈振荡衰减变化规律,最大飞行攻角为6°,落地时刻飞行攻角衰减为0。
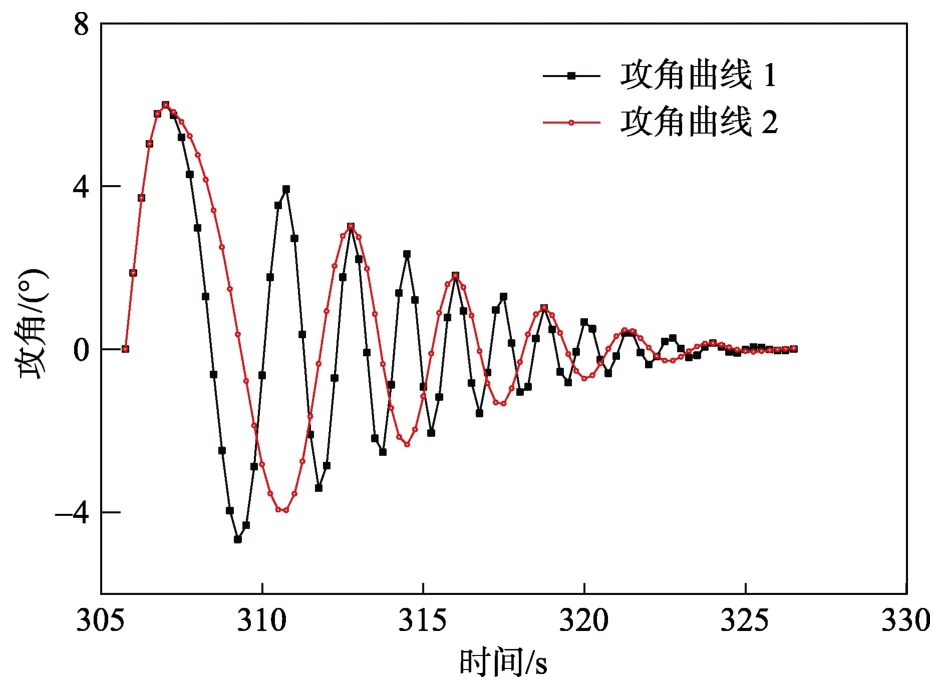
图5 再入攻角曲线Fig.5 The curve of attack angle
再入飞行过程中,在攻角曲线1 的情况下,锥身截面不同子午面冷壁热流密度变化曲线如图6 所示。从图6 可以看出,90°子午面热流密度变化曲线与零攻飞行时相同,再入飞行攻角振荡对该子午面无影响。
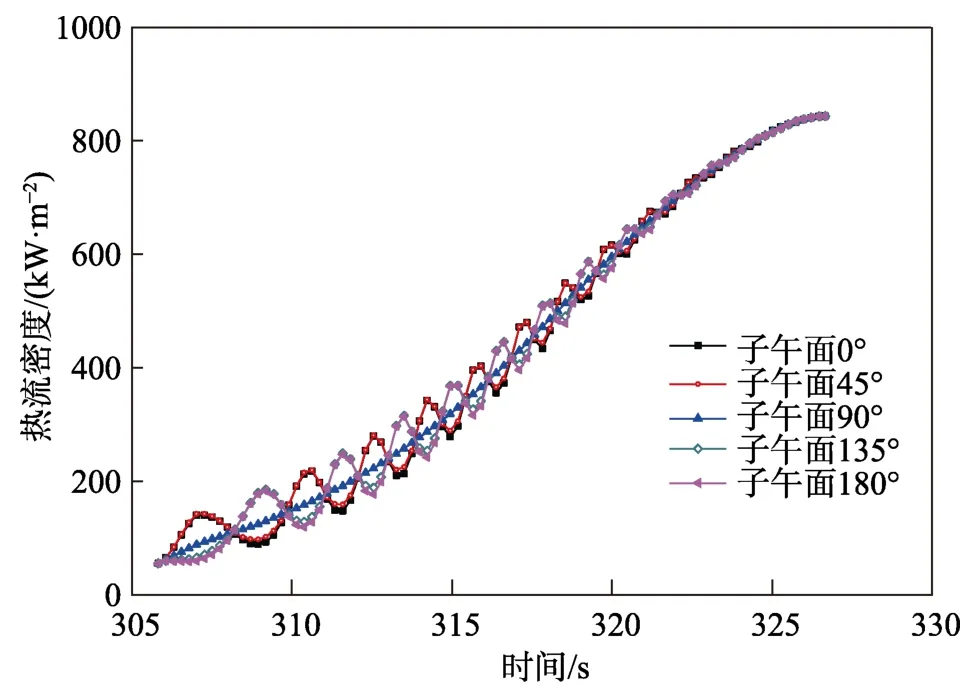
图6 不同子午面热流密度变化曲线Fig.6 The heat flux curve on different meridian plane
随着再入攻角的振荡衰减,非90°子午面冷壁热流密度曲线围绕90°子午面热流密度曲线振荡,且其振荡频率与攻角振荡频率一致。相对于90°子午面,迎风子午面热流密度呈正攻角增大、负攻角减小的变化规律;背风子午面热流密度则随攻角表现为正攻角减小、负攻角增大的变化规律。
各子午面热流密度相对于90°子午面的振幅表现为先振荡增大、后振荡衰减的变化规律,且越接近于90°子午面,振幅越小。当t=312.5 s 时,热流密度振荡幅值达到最大。由于各子午面热流密度振幅与90°子午面热流密度大小、攻角振幅均密切相关,因此,振幅最大时刻处未出现在攻角最大时刻处。
同时,相同攻角幅值时,正攻角引起的热流密度增大量大于负攻角引起的热流密度减小量。当t=312.5 s 时,正负攻角引起的热流密度振荡增幅分别为26%、–20%。
再入飞行过程中,锥身截面典型子午面总加热量见表1。可以看出,再入飞行攻角振荡衰减时,各典型子午面总加热量各不相同。与90°子午面总加热量(与零攻时总加热量相同)相比,各子午面总加热量均有所增大,最大增幅为1.7%。虽然在攻角振荡较大位置处,热流密度的变化幅度较大,但由于攻角振幅的衰减以及正负攻角对热流密度影响的叠加效应,导致壁面总加热量增幅较小。

表1 非零攻再入时不同子午面总加热量Tab.1 The total reentry heat transfers having attack angle on different meridian plane
在攻角曲线1 的情况下,锥身截面不同子午面典型位置处温度历程曲线如图7 所示。锥身截面不同子午面最终时刻温度见表2。对于金属层外壁面,再入攻角对各子午面温度的影响规律与热流密度相同。再入飞行过程中,攻角振荡可使金属层外壁面温度振荡幅值达到3 K,但最终时刻各子午面外壁面温差小于1 K,攻角振荡对最终时刻温升影响较小。由于金属层的热沉作用及隔热层的隔热作用,攻角振荡对金属层内壁面各子午面温度影响进一步减弱,对隔热层各子午面温度基本无影响。

表2 锥身截面不同子午面最终时刻温度Tab.2 Temperature at last time on different meridian plane

图7 锥身截面不同子午面各典型位置处温度曲线Fig.7 The temperature curve on different meridian plane on(a) metal outer wall,(b) metal inner wall and (c) heat insulation layer inner wall
不同攻角振荡频率时,典型子午面热流密度变化曲线如图8 所示,不同子午面各典型位置温度曲线如图9 所示。可以看出,当攻角振幅相同、频率减小时,0°、180°子午面热流密度相对于90°子午面的振幅保持不变,振荡频率相应减小。随着振荡频率的减小,0°、180°子午面总加热量有所增大,但对于计算采用的攻角振荡曲线,增幅较小。攻角振荡频率对金属层外壁面温度影响规律与对热流密度的影响规律相同,对金属层内壁面影响进一步减弱,对隔热层基本无影响。
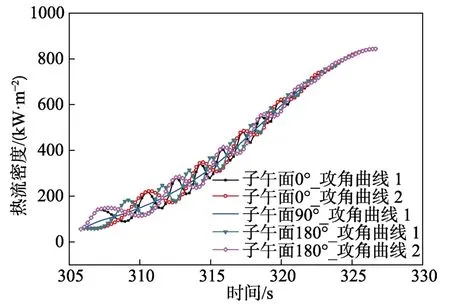
图8 不同攻角振荡频率时典型子午面热流密度变化曲线Fig.8 Typical heat fluxcurve with different attack angle oscillation frequencyies
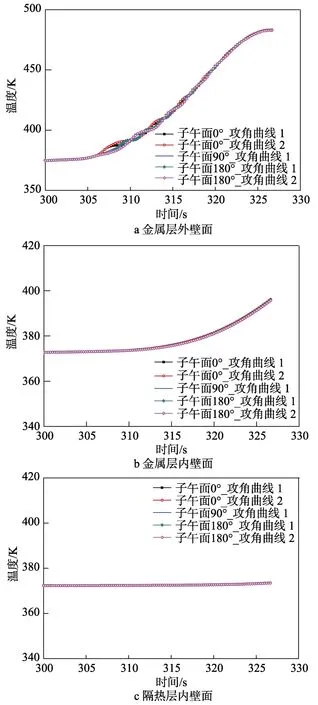
图9 不同攻角振荡频率时不同子午面各典型位置温度曲线Fig.9 The temperature curve with attack angle oscillation frequency in different meridian planes on (a) metal outer wall,(b)metal inner wall and (c) heat insulation layer inner wall
4 结论
建立了基于工程法的气动热/结构热响应耦合计算方法,并基于以上计算方法开展了某火箭测试平台弹头锥身典型位置气动热环境及结构热性特性分析,研究再入攻角振荡对气动热环境及结构热响应特性的影响规律。得出以下结论:
1)随着再入攻角的振荡衰减,各子午面冷壁热流密度曲线围绕90°子午面热流密度曲线振荡,其振幅呈现先振荡增大、后振荡衰减的变化规律,且越接近于90°子午面,振幅越小。计算攻角条件下,与90°子午面总加热量相比,各子午面总加热量均有所增大,最大增幅为1.7%。
2)再入攻角对各子午面金属层外壁面温度的影响规律与热流密度相同,再入过程中,金属层外壁面温度最大振荡幅值为3 K,但对最终时刻结构温度影响较小。
3)计算攻角条件下,攻角振荡频率对典型子午面热流密度增幅无影响,对壁面总加热量、最终时刻结构温度影响较小,其影响可通过增加余量的方式给予考虑。
4)考虑再入攻角影响时,该火箭测试平台弹头锥身壳体防隔热方案仍满足设计要求,可用于飞行试验。

