可压缩流动脉动压力数值模拟求解器HFS 研究

（中国工程物理研究院总体工程研究所，四川 绵阳 621999）

高速飞行器在飞行过程中将可能经历高温真实气体效应、稀薄气体效应、黏性干扰、边界层转捩和分离以及热辐射等复杂物理化学现象[1-4]。由于实验研究难度大，成本高，数值模拟成了重要的研究途径之一。高速飞行中会出现各种特殊流动现象，如激波与边界层的相互干扰、边界层传热传质、化学反应以及烧蚀。高速飞行器的内外流动以湍流及转捩为主要特征。层流转捩到湍流后，摩阻及热流增加为原来的数倍。因而，无论气动力还是热防护设计，都需要对转捩与湍流进行精细预测。此外，燃料混合、气动光学以及气动声学都与湍流及转捩密切相关，这就对湍流及转捩的机理、模型及控制提出了严格的要求。目前数值模拟湍流的主要手段[5-8]有直接数值模拟（DNS）、大涡模拟（LES）、雷诺平均Navier-Stokes方程（RANS）以及RANS/LES 混合模型（如DES）。

直接数值模拟是目前最为准确可靠的湍流计算手段[5,9-10]，它不引入任何湍流模型，而是直接求解Navier-Stokes 方程，以获得流场的所有时间尺度和空间尺度的细节。要捕捉全部时空演化细节，要求计算的网格尺度比流场结构的空间尺度小，同时时间步也要足够小以捕捉相应的时间尺度，因此DNS 的网格量十分巨大。与此同时，湍流中的小尺度结构很容易被计算格式的数值耗散耗散掉，从而导致流场细节的丢失。因此，对湍流进行直接数值模拟时，要求数值格式的数值耗散要小。中心型数值格式往往具有低耗散或者无耗散，例如中心差分格式和中心型紧致格式，但是这些数值格式在计算含数值间断问题（如激波）时，往往会在间断附近产生数值震荡而使计算失败。要捕捉间断，必须往数值格式里引入一定的数值耗散以抑制间断附近的数值震荡，例如使用激波捕捉格式（如TVD 格式[11]、ENO 格式[12]、WENO 格式[13]等）。高分辨率所需的低耗散与保持计算稳定的高耗散这一对矛盾很难平衡，尤其是对于高速湍流[11]。在计算流体力学（CFD）的高精度数值算法当中，基于非结构网格的高精度方法目前尚未成熟，在模拟含间断的流动时鲁棒性较差，同时计算量和内存占用较大，在实际工程中运用较少。基于结构网格的高精度有限差分方法具有成熟的数值方法，计算代价小，是工程中最实用的高精度方法。然而对于复杂几何外形的流场，由于难以生成高精度的网格，实际计算中会引入网格几何误差，处理不慎会影响计算结果的准确性。邓小刚等[14]指出当数值格式满足几何守恒律时，可以消除网格不光滑带来的几何误差，其中加权紧致非线性格式（WCNS）[15-19]就是其中最典型的一种。文中求解器主要采用WCNS 格式作为空间离散格式，以确保计算高速流动中的稳定性。

综上所述，通过数值模拟研究可压缩流动尚存在许多技术难点。文中旨在发展一套能够模拟复杂几何构型的可压缩流动的高精度求解器，并利用该求解器研究高速下钝头体的绕流流动。

1 数值方法

为了模拟复杂几何构型的流场，一般采用曲线坐标系下的可压缩Navier-Stokes 方程，其形式为：

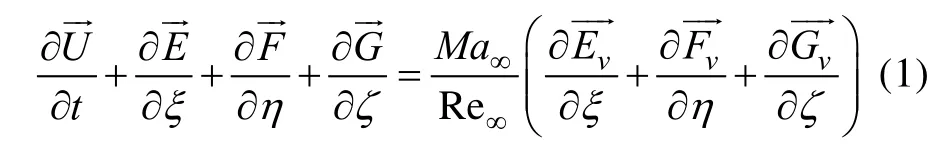
式中对流通量分别为：

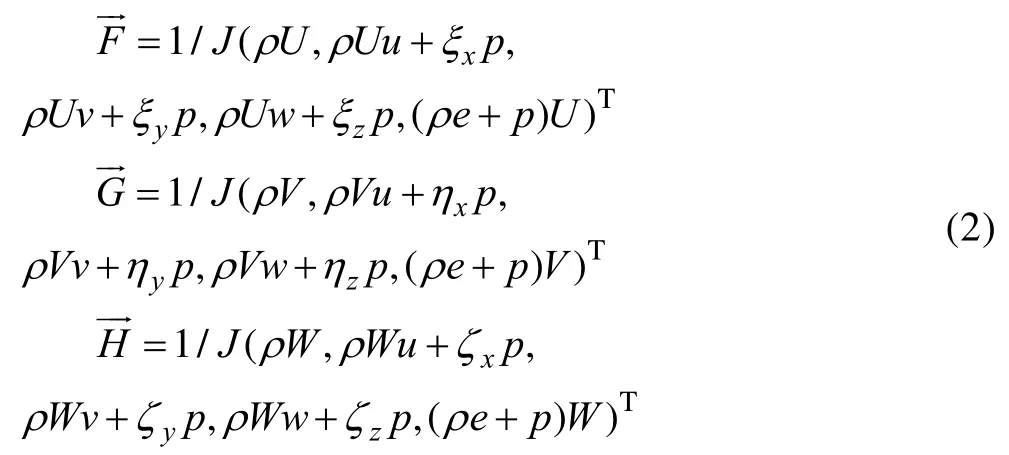
黏性通量分别为：

式中：τij是黏性应力张量；βi=μjτij+qi，qi为热通量，黏性系数μ由Sutherland 公式确定。

为了准确捕捉激波，对流项采用显式加权紧致非线性格式（WCNS-E）进行离散：

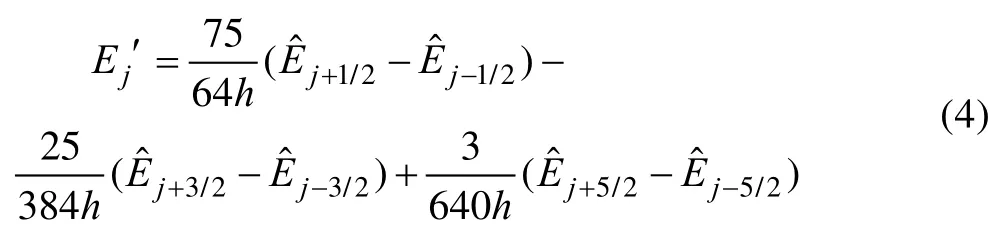
WCNS 格式的核心思想是，将一个大的点模板拆分为若干小的模板的线性组合，如式（5）所示。

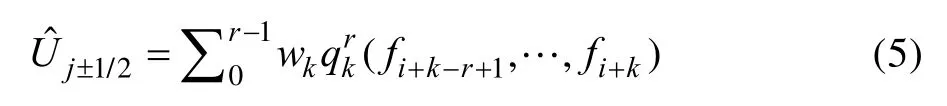
引入如式（6）所示的非线性权：

通过评估每个小模板的光滑程度，调整每个子模板的权重。对于含间断的子模板，权重自动设置为一个极小的值，从而消除不光滑模板的贡献。对于5 阶WCNS-E 格式，具体计算方法如下所述。

将插值变量到特征空间：

对特征进行高阶插值：

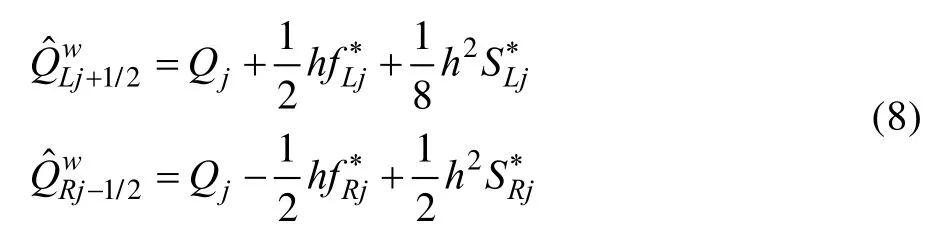
式中：f、S分别为一阶导数及二阶导数的近似。

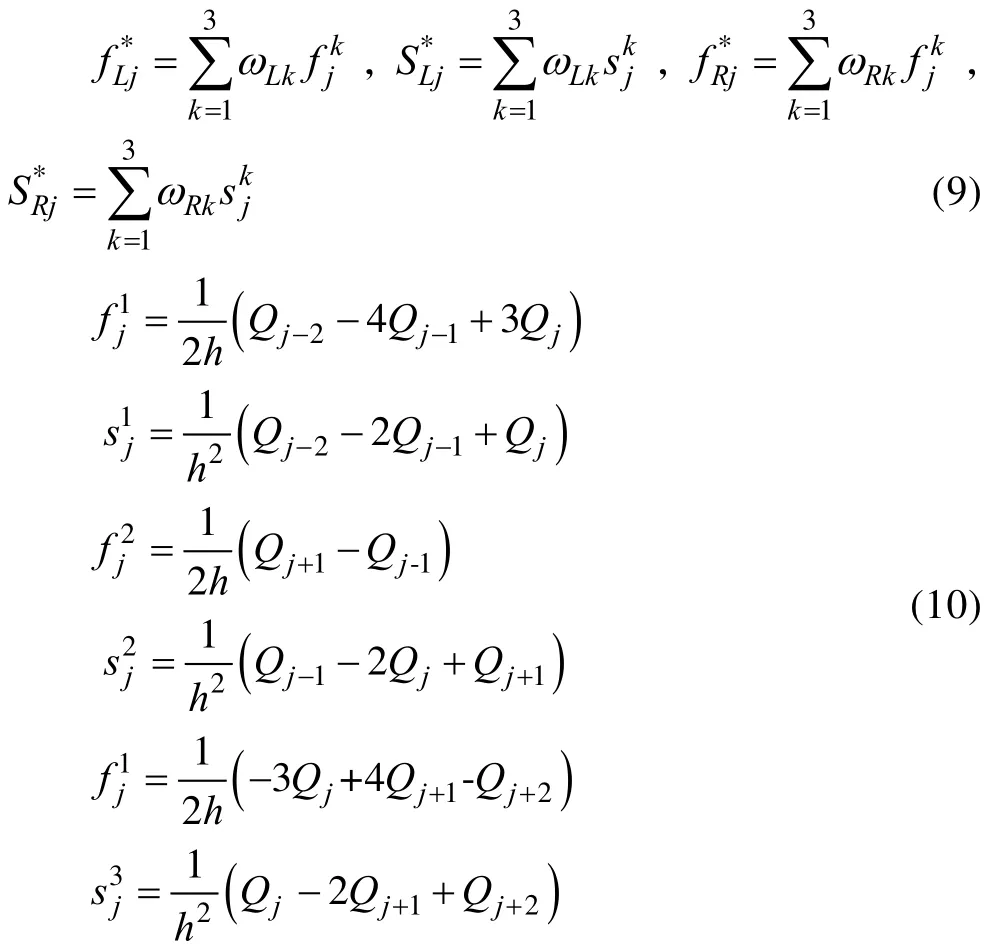
ω为权重，定义为：

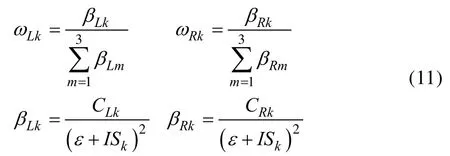
式中：ε是为避免分母为零而加的小量，ε=10－6。ISk为模板的光滑性度量，由式（12）计算：

CLk和CRk为优化权重：

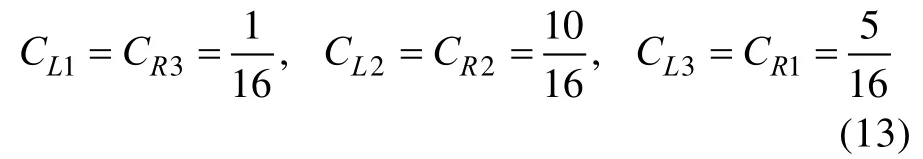
为了匹配高精度的空间离散格式，时间离散通常采用显式Runge-Kutta 格式。文中采用3 阶精度的TVD Runge-Kutta 格式，如式（14）所示：

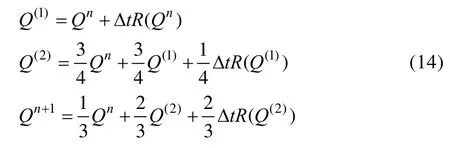
2 验证算例

2.1 Blast wave 测试

Blast wave 测试[20]描述的是两道相向运动的强间断相互作用，是考核程序的鲁棒性和间断捕捉能力的经典算例。该算例的初始条件设置如式（15）所示：

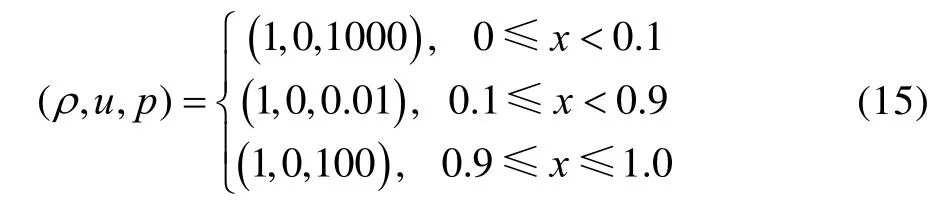
计算域为x∈[0,1]，在x=0 与x=1 位置施加反射边界条件。计算域采用均匀网格离散，网格点数为N=400，计算无量纲时间t=0.038。“精确解”为WENO5-JS 格式，用网格点N=2500 计算获得。

测试结果（如图1 所示）表明，采用不同的WCNS格式，可以看出当前程序求解的结果都能稳定且准确地捕捉强间断，并且与参考解吻合良好。证明了程序采用数值格式的在处理强间断能保持很好的鲁棒性。

2.2 NACA0012 翼型绕流算例

该算例旨在考察程序模拟复杂几何构型流场的能力。自由来流条件设置如下：来流马赫数为0.8，基于弦长的雷诺数为500，攻角α=10°。NACA0012翼型弦长为1，周向分布377 个网格点，径向74 个网格点，近壁处最小法向网格距离为1.7 mm。翼型前缘网格区域扩展到18 倍弦长，后缘到35 倍弦长。出口和入口都采用远场黎曼边界条件，翼型表面采用无滑移、无穿透壁面边界条件，展向依然采用滑移壁面边界条件，翼型区域总网格大小为377×74×21，后缘到网格最右端网格大小为68×74×21。计算结果如图2 和图3 所示。

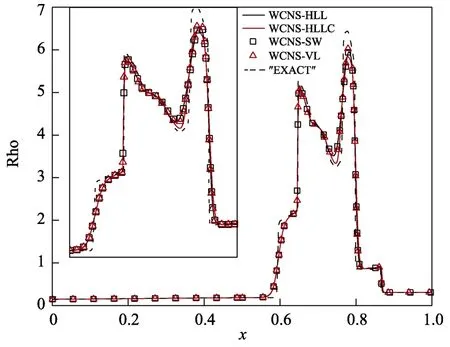
图1 Blast wave 测试算例Fig.1 Blast wave case

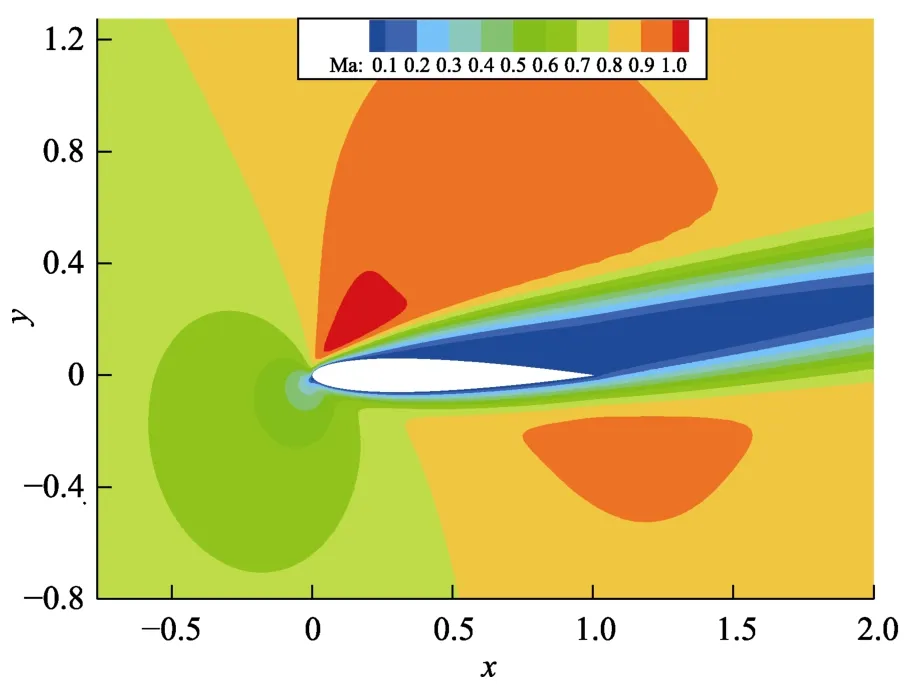
图2 NACA0012 翼型马赫数分布Fig.2 Mach filed around NACA0012

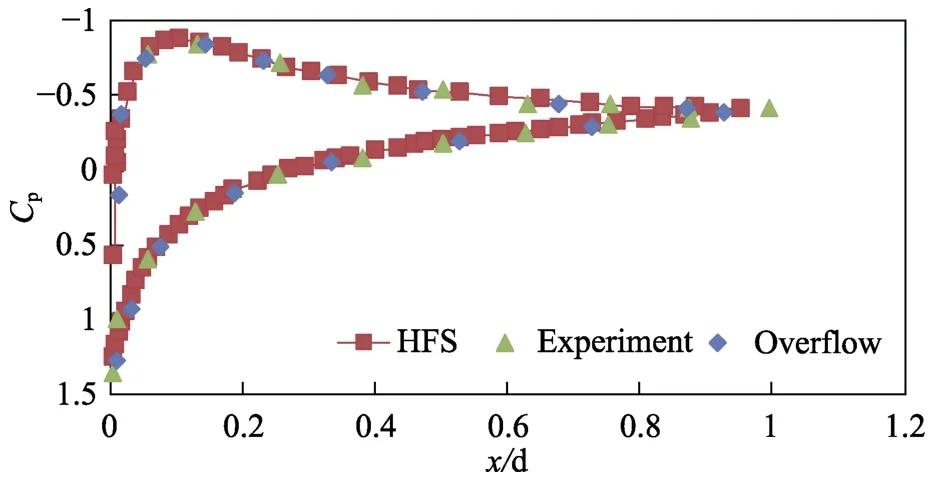
图3 不同求解器得到的NACA0012 翼型表面压力曲线分布对比Fig.3 Comparison of the curve of pressure on the surface of NACA0012 by three different solvers

图2 为HFS 计算得到的机翼流场马赫数等值线分布，可以看出，流场中的等值线非常光滑平顺。图3 显示了机翼表面的压力系数，并将HFS 的计算结果与NASA 的OVERFLOW 程序的计算结果和实验结果进行了对比。结果显示，HFS 的结果与OVERFLOW和实验测量结果均符合良好，验证了HFS 程序计算可压缩黏性流场的能力和准确性。

2.3 钝锥表面脉动压力分析

该算例旨在考察模拟钝锥边界层流动的能力。自由来流条件设置如下：来流马赫数为6，单位长度雷诺数为107/m，头部半径为1 mm，壁面扰动边界条件见李新亮等[21]，扰动幅值为0.005。沿钝锥母线方向分布3600 个网格点，周向分布1500 个网格点，沿壁面法向分布360 个网格点，在钝锥尾部部署200 个拉伸网格用于吸收人工截断带来的数值扰动，壁面采用无滑移+吹吸气扰动边界条件，远离壁面采用无反射边界条件。从图4 和图5 中可以看出，钝锥外部流动分为3 个明显的区域，初始为层流阶段，依次经历转捩和完全发展湍流，后续将继续利用HFS 求解器研究钝锥扰流的脉动压力的时空分布规律。

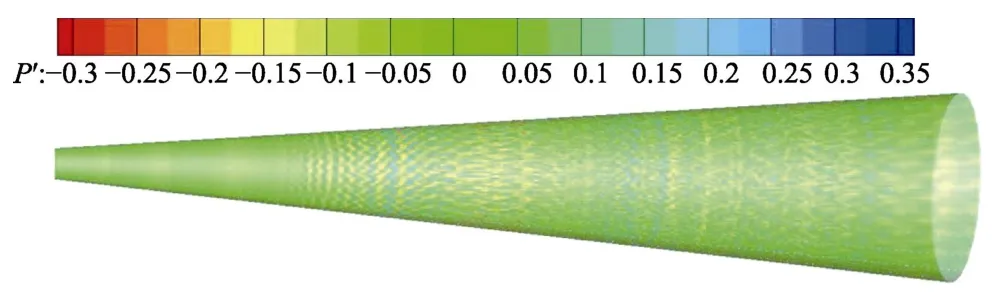
图4 钝锥表面脉动压力云图Fig.4 Fluctuation pressure on the surface of a blunt-body

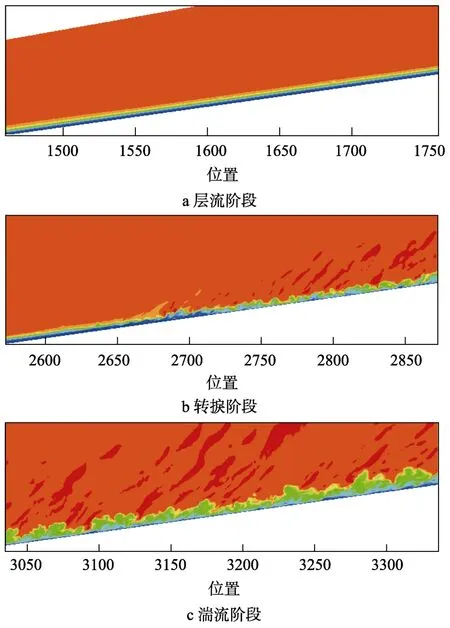
图5 钝锥外部的脉动压力云图Fig.5 Fluctuation pressure near the surface of a blunt-body:a) laminar flow stage;b) transition stage;c) turbilent stage

3 结论

1）开发了一套可压缩流动脉动压力求解器，并通过几个算例验证了数值格式、边界条件等的正确性。

2）研究了钝锥扰流，捕获了钝锥边界层的层流、转捩和完全发展湍流等流动现象，获得了壁面脉动压力的空间分布。