基于有限元法的随机振动与噪声复合响应数值模拟分析
(中国工程物理研究院总体工程研究所,四川 绵阳 621999)
再入飞行器在贮存、运输、机动及飞行全任务剖面中,将遭受各种环境因素的影响,其中,再入环境的影响尤为突出。再入飞行时,外表面的高速绕流流场将诱导复杂的振动、噪声等环境,结构振动引起气体介质振动,从而产生声波,声波产生压力又反作用到结构上,有可能产生复杂的环境效应(如结构破坏、可靠性和安全性问题),而且外表面的高速绕流流场产生脉动压力频段较高。因此,需要开展宽频域随机振动、噪声的复合响应分析方法研究。
由于随机激励时间较长,工程上通常将时域随机载荷转换为频域功率谱进行加载。对于声振耦合分析,在中低频段且仅包含内声场时,可采用模态叠加法进行求解。但在结构包含外声场时,为避免边界能量反射,需将声场边界描述为可吸收能量的无限远边界条件。这时边界处将产生能量损耗,模态求解得到的为复特征值,而现有商业软件中没有利用复特征值进行模态叠加开展随机振动分析的方法[1-5]。在高频段,结构模态密集度非常高,有限元模态求解误差较大,采用模态叠加法进行宽频域随机振动分析在工程应用中也比较困难。统计能量法是解决高频振动问题的有效方法,它关心空间上的统计平均值,是一种从全局出发的模块化方法,得到结构或子结构的响应均值,无法得到具体位置的响应,并且统计能量法也不适合中低频段结构振动响应分析[6-9]。
流固耦合分析方法大致可分为直接耦合方法和间接耦合分析方法,直接耦合方法计算时包含所有必要量的单元矩阵或单元载荷矢量,通过对包含所有自由度的耦合单元直接进行求解,实现流体和结构的耦合;间接耦合是流体计算和结构计算交替进行,在一种场里计算后,导出耦合界面的结果,在另一种场里导入,成为耦合界面的载荷,进行耦合计算[10-13]。
为避开模态叠加法和统计能量法的求解局限,文中拟采用直接耦合方法建立声场-结构直接耦合的动力学有限元模型,以直接法谐响应分析为基础,结合理论分析实现宽频域随机振动和噪声复合响应分析。
1 基于声学流体的流固耦合动力学有限元理论
在进行基于声学流体的流固耦合分析时,需要把流体斯托克斯方程与结构的动力方程综合考虑,这时可得到完整的基于声学流体的流固耦合问题的有限单元法动力学离散方程:
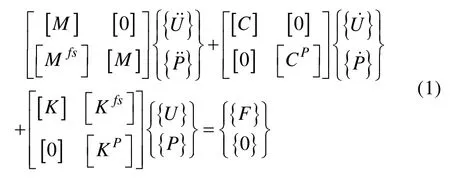
式中:{P}为节点声压向量;{U}为节点位移向量;{F}为节点载荷向量;[M]为结构质量矩阵;[K]为结构刚度矩阵;[C]为结构阻尼矩阵;[MP]为声场流体质量矩阵;[KP]为声场流体刚度矩阵;[CP]为声场流体阻尼矩阵;[Mfs]为流固耦合界面的质量矩阵;[Kfs]为流固耦合界面的刚度矩阵。
与不考虑声场时的结构振动离散方程相比,式(1)中由于考虑了流固耦合效应,质量矩阵和刚度矩阵都是非对称性的,给基于对称矩阵的特征值求解方法带来了一定的困难,因此需要采用基于非对称矩阵的特征值求解方法进行模态分析。
由振动理论[14]可知:当激励f(t) 为各态历经稳态随机过程时,结构上某点位移响应的功率谱为:
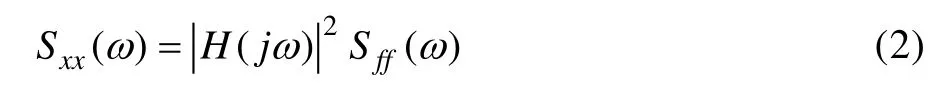
加速度响应的功率谱为:
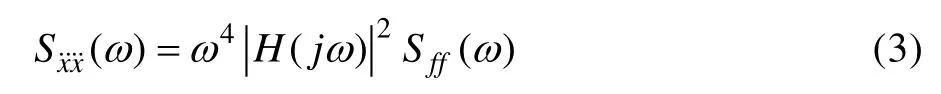
式中:Sff(ω)为激励f(t)的功率谱;H(jω)为频响函数矩阵。
因此,可首先采用直接法进行谐响应分析,获得结构的频响函数,再根据式(2)和(3)获得已知随机激励下结构的位移和加速度响应功率谱曲线,同样也可获得结构上某位置的应力、应变等响应功率谱曲线。
2 实例分析
2.1 声振耦合动力学有限元模型
建立如图1 所示的结构与内声场耦合模型(为降低计算规模,未考虑外声场),结构参数:弹性模量为70 GPa,密度为2000 kg/m3,泊松比为0.3。空气的密度为1.29 kg/m3,空气中的声速为343 m/s。
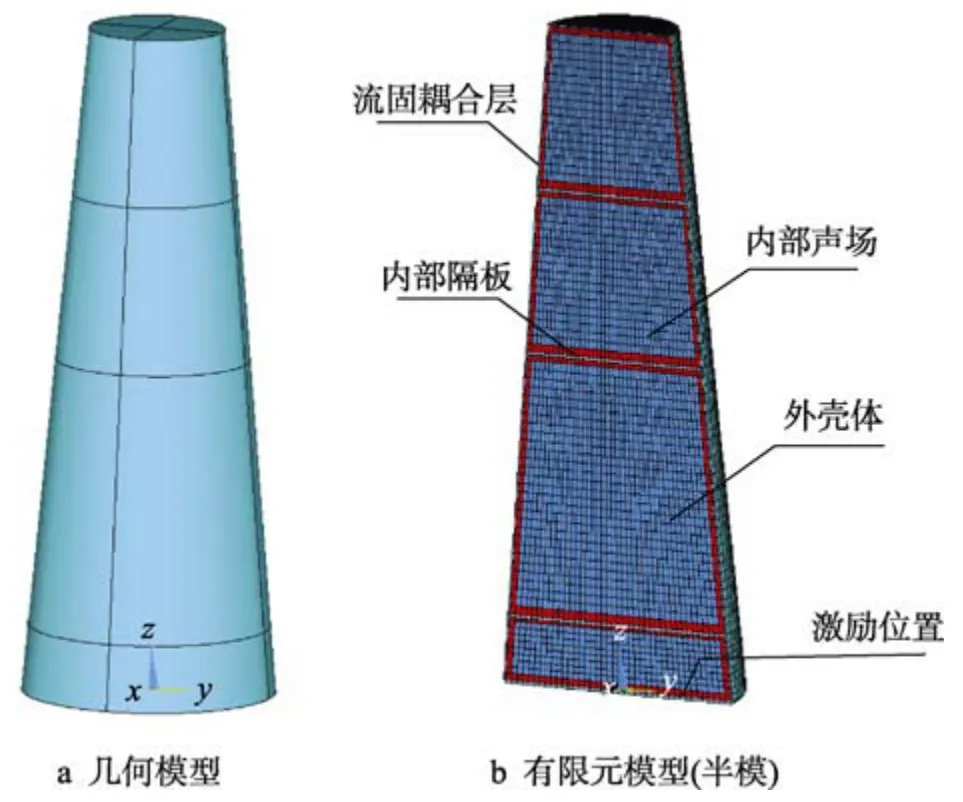
图1 结构与声场耦合模型Fig.1 Structural-acoustic finite model:a) geometric model;b)finite element model(half model)
2.2 模态分析结果
在进行流固耦合模态分析时,边界条件采用自由状态,排除掉自由模态,对考虑流固耦合的模态与仅结构的模态固有频率结果进行对比,频率见表1,振型如图2 所示。
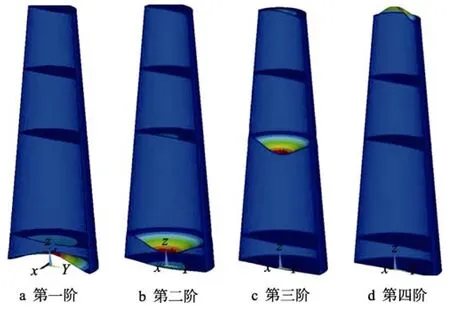
图2 模态振型Fig.2 Mode shape:a) first order;b) second order;c) third order;d) fourth order

表1 流固耦合模态与仅结构模态固有频率结果比较Tab.1 Comparison of natural frequency results between fluidstructure interaction mode and structure-only mode Hz
2.3 随机振动分析结果
在图1b 中激励位置所在的框施加加速度功率谱密度为0.01g2/Hz,频段为10~5000 Hz 的基础激励,采用直接法获得关注点的频响函数。然后根据式(2)和式(3)获得关注点的功率谱密度曲线。从上到下五层板中心仅结构和考虑声固耦合的加速度响应如图3 所示。
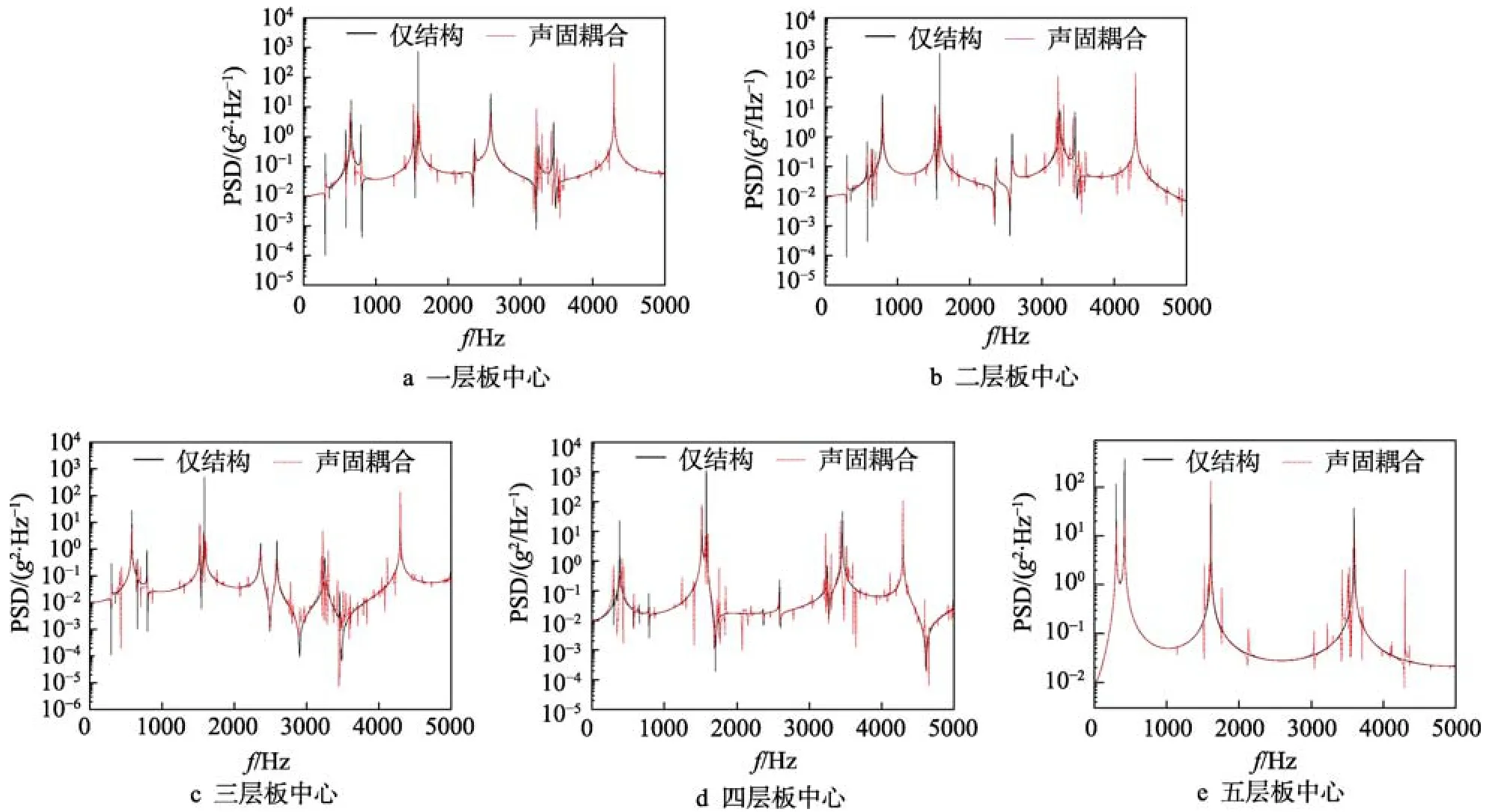
图3 仅结构模型和声振耦合模型不同位置加速度响应功率谱对比(g=9.8 m/s2)Fig.3 Comparison of power spectrum of acceleration response at different positions between structural-onlymodel and acoustic-vibration coupling model (g=9.8 m/s2):a) first floor plate center;b) second floor plate center;c) third floor plate center;d)fourth floor plate center;e) fifth floor plate center.
3 结论
1)基于声学流体,根据非对称矩阵的特征值求解方法获得了结构声固耦合模态。采用商业有限元软件直接法谐响应分析模块,获得结构频响函数曲线,以结构频响函数曲线为基础结合理论分析可间接得到结构随机振动功率谱响应曲线。
2)分析结果表明,考虑声振耦合时,噪声对结构的固有频率变化不大。
3)考虑声固耦合与仅结构状态相比,薄壁结构有的频段加速度响应放大,噪声有放大效应;有的频段加速度响应衰减,噪声起到阻尼效应。

