基于CLG光学流和波场分解的逆时偏移角度道集提取方法研究

吴成梁， 王华忠， 冯波， 盛燊

同济大学海洋与地球科学学院波现象与智能反演成像研究组， 上海 200092

0 引言

角度域共成像点道集(ADCIGs)包含背景速度和地下角度反射系数的信息，对于速度建模和储层描述具有重要意义．与克希霍夫偏移、Beam偏移和单向波偏移相比，逆时偏移(Baysal et al.，1983；Whitmore，1983)能够精确地处理横向变速情况以及多波至现象，克服陡倾角限制，成为了复杂介质的首选成像方法.逆时偏移角度道集可以采用扩展成像条件方法(Sava and Fomel，2003，2006；Fomel，2004；Duveneck，2013)或局部平面波分解方法(Xie and Wu，2002；Xu et al.，2011；Yan and Xie，2011，Tang et al.，2013；Hu et al.，2015)实现．扩展成像条件方法首先生成地下局部偏移距道集，然后借用倾斜叠加等方法转换为地下角度道集．局部平面波分解方法需要将波场分解为局部平面波分量，应用角度域成像条件提取角度道集，计算代价较大．在逆时偏移角度道集中，算法的高效性和并行性是制约高效提取角度道集的重要因素．波矢量方向估计方法(Yoon et al.，2004；Yoon and Marfurt，2006；Dickens and Winbow，2011；Vyas et al.，2011a，b；Zhang and McMechan，2011a，b；王保利等，2013；Jin et al.，2014；Yoon，2017)在逆时偏移角度道集生成方法中是一类比较高效的方法．

在波矢量方向估计方法中，可以通过任意空间和任意时刻的振幅和相位梯度来计算传播方向．一旦估计出震源波场和检波点波场的方向矢量，就可以计算出反射张角和方位角，并利用互相关成像条件提取成像道集．在波矢量估计方法中，可以采用坡印廷矢量方法计算波场传播方向．由于坡印廷矢量方法计算高效，具有较高的角度分辨率，在逆时偏移角度道集生成方法中被广泛地应用．但是由于在检波点端波场比较复杂，此时计算的坡印廷矢量通常会出现不稳定情况，Yoon等(2011)和Vyas等(2011a)提出利用坡印廷矢量计算震源端波场传播方向和地下反射界面倾角来估计反射角；Zhao等(2012)提出通过偏移剖面预测反射层法向向量，利用稳定的震源端方向波场结合反射层法向向量来计算角度道集．虽然坡印廷矢量方法比较高效，但是该方法无法处理波前重叠问题(Patrikeeva and Sava，2013)．

在生成逆时偏移角度道集中，外推波场的方向也可由光学流方法计算．光学流最先由Gibson于1950年提出，被广泛应用于解决连续图像帧之间的视运动问题．目前有许多种计算光学流场的方法(Sobey and Srinivasan，1991；Barron et al.，1994；Brox et al.，2004；Bruhn et al.，2005；Szeliski，2010)．其中Lucas-Kanade方法(LK，或称局部方法)(Lucas and Kanade，1981)和Horn-Schunck方法(HS方法，或称全局方法)(Horn and Schunck，1981)是两类主要的方法，其他方法大都是基于上述方法的补充．Vyas等(2011a)应用LK光学流方法生成角度道集，Zhang(2014)采用HS光学流方法估计波场方向，提取角度道集．然而，LK光学流方法容易出现奇异现象，依赖于局部点的梯度值，而HS光学流方法依赖于整体的能量约束，距离较远的波场也会参与到波场方向计算中，导致计算的波场方向精度较低．

本文提出采用CLG(Combining Local and Global)光学流方法计算波场方向，提高波场方向的精度．CLG光学流方法结合局部LK方法和全局HS方法的优点，在施加全局约束的基础上，考虑局部点的加权作用，在保持波场方向估计稳定的基础上，提高估计的波场方向精度．另外，为了弱化光学流方法无法处理波前重叠问题，本文提出利用解析波场对波场进行方向分解，将分解后的行波分别成像，提取角度道集．进一步地，在提取角度道集过程中，需要将光学流场计算的波场方向转换为反射张角和方位角，本文提出一种有效的归一化方法和改进的最小二乘除法，提高角度计算的准确性，避免带限子波引起的角度计算的不稳定．最后，采用角度道集面元化和规整化来优化角度道集．

1 方法理论

1.1 波场方向估计

光学流问题的基本假设可以描述为后续时刻外推的波场值不随时间变化：

u(x+Δx,y+Δy,z+Δz,t+Δt)=u(x,y,z,t),

(1)

其中(x,y,z)是地下空间坐标，t代表时间，u是波场．基于小位移假设，采用一阶泰勒展开可得到光学流方程．

ux·vx+uy·vy+uz·vz+ut=0,

(2)

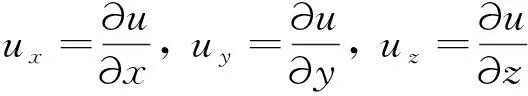
(ux,v)+ut=0,

(3)

其中x=(x,y,z)，v=(vx,vy,vz)，ux=(ux,uy,uz)．由于在方程(3)中未知量的个数大于方程的个数，该问题是一个欠定问题，需要引入额外的约束求解该问题．

在局部LK光学流方法中，通过假设未知的光学流矢量在局部邻域Ω内是恒定不变的，构建如下加权最小二乘泛函求解上述光流问题：

(4)

其中WΩ为在局部邻域Ω内的加权系数，最小化ELK(v)得到如下线性方程组：

(5)

在每个外推时刻逐个空间点求解上述3×3的线性方程组即可得到光学流场．LK光学流方法计算量小，只受局部范围的影响，距离当前点较远区域的误差不会影响当前点的计算，误差不具有传播性．但是LK方法不稳定，当梯度消失时，线性方程组会出现奇异现象．因此，LK光学流方法通常在稀疏场中实现，然后采用不同的插值方法插密．此外，光学流的精度依赖于方程组中梯度张量的准确性．

在全局HS光学流方法中，通过引入额外的全局能量的信息约束，求解上述欠定问题，构建如下的误差泛函：

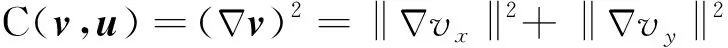
(6)

(7)

其中Δ为拉普拉斯算子．全局HS光学流方法通过引入整体的能量约束，避免出现奇异现象，即使在某些点上没有梯度值，但是由于全局能量约束，也能比较稳定地求解光学流场，因此该方法能产生较密的光学流场．然而波场的传播具有局部方向性，整体的能量约束带来的问题是，距离计算点较远区域的波场也会参与到当前点的计算中，导致计算的波场方向精度有所下降．

结合局部邻域变化特征和全局的能量约束，本文提出构建如下的CLG光学流误差泛函：

(8)

(9)

CLG光学流方法不仅克服了梯度为零时无法估计光学流问题，而且实现了局部约束以提高抗噪性．采用CLG光学流方法估计的波场方向更加精确和稳定．对比HS光学流方法(方程(7))，CLG光学流方法增加的计算量并不大．方程(9)和方程(7)的迭代格式是一致的，比较容易实施并行化处理，方便融合在逆时偏移的波场外推过程中．

1.2 波场方向分解

采用CLG光学流方法可以计算波场方向．但是光学流方法的假设前提是在每个成像点每个成像时刻只有一个传播方向．因此，该方法不能处理波前重叠的情况．本文采用解析波场和空间傅里叶变换对外推的波场进行行波方向分解，将分解后的行波分别计算光学流场，提取波场传播方向构建角度道集．

在解析波场中，仅包含正频率信息，仅需对波场实施空间域的傅里叶变换即可实现波场分解，从而可以避免时间维的傅里叶变换．解析波场是复数波场，其实部可通过波动方程外推获得，其虚部可通过对地下波场进行Hilbert变换得到．但是由于Hilbert变换是关于时间方向的卷积，理论上需要将整个波场存盘并进行卷积，对内存和存储要求比较大．借助于波动方程的源项和波场具有线性关系(Liu et al.，2006)，把对波场的Hilbert变换转化为震源项的Hilbert变换，利用新的“震源”进行传播，从而构建出解析波场的虚部(Hu et al.，2015)．以震源端为例，震源端的解析波场如下所示：

(10)

(11)

(12)

其中F算子代表傅里叶变换，ks为波数．因此，可以根据波数关系提取任意方向、任意角度宽度传播的波场．

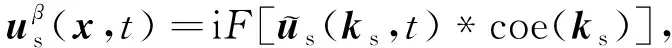
(13)

虽然理论上可以提取任意角度的波场．但是在逆时偏移过程中，波场方向分解需要付出较多的计算代价．为了平衡计算代价和方向估计精度，我们可以根据地下介质的特征进行适应性的选择．若把地下介质抽象为在空间上广泛分布的缓变的层状沉积层，加上火山活动，构造运动等引起的大、小尺度的速度异常体(或波阻抗变化的异常体)(王华忠等，2015)．则只需要采用上下行波分解即可满足大部分的成像需要，能够在一定程度上弱化波前交叉问题．此时行波分解可以简单的写成下式：

(14)

(15)

1.3 反射张角和方位角估计

光学流方法计算的波场方向矢量代表了波场的运动差异．在估计反射张角和方位角之前，需要实施归一化处理．本文在归一化过程中通过采用对光学流和波场同时约束，避免噪音干扰和弱值的影响．

(16)

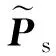
反射张角θ和方位角φ一般可通过下式计算：

(17)

(18)

其中nx=(1,0,0)和nz=(0,0,1)分别为单位矢量．但是由于地震波是振荡的．在计算反射张角和方位角时，涉及到除法，分母较小的位置会使得除法变得非常不稳定．为了提高角度估计的稳定性和精度，以及保护弱反射信号，我们采用最小二乘反演方法估计反射张角和方位角：

(19)

(20)

其中Ω={x,t}是关于时间和空间的局部平滑窗，在本文的测试中，仅采用了关于空间的平滑窗．

当方向矢量值较小时会导致反射张角计算错误，并且计算错误的反射张角几乎为90°．对于偏移成像，较大的入射角通常对应需要滤除的低波数噪音．因此，本文采用改进的最小二乘法来估计反射张角，把因方向矢量过小计算错误的角度值转移到更大的入射角度中，避免污染成像道集．最终计算反射张角的法方程为

(21)

1.4 角度域成像条件

(22)

1.5 角度道集面元化和规整化

由于采集的不规则地震数据，复杂的地下传播路径，在地下角度域中成像道集是不规则的．在成像点处，不同角度面元和地下不同位置的角度道集覆盖情况是不同的．随着地下空间位置的不同，角度道集会出现欠采样和过采样问题，实际的地下角度采样是散乱不规则的．另外，由于数值计算的离散化问题，实际的角度道集不能放在正确的放置，不同的角度面元间隔会使得最终的不同角度的叠加次数不同，影响AVA分析．离散的、不规则的角度道集需要在角度域实施面元化处理．在本文中，我们采用角度插值方法对角度道集进行面元化和平滑．进一步地，还需要考虑角度照明和覆盖问题．

另外，由于偏移速度的不准确、地震子波的空间变化以及地下介质的复杂性，角道集可能会出现剩余深度时差和子波拉伸等现象．成像道集后处理技术，如动态时间规划和局部相似叠加(Wu et al.，2019)，可用于优化角度道集，提高成像道集质量．

2 数值实验

基于CLG光学流和波场分解提取角道集流程如图1所示．考虑实际的多炮地震数据特征和当前的计算机集群的结构特点，本文采用MPI主从模式对炮数据并行，在每个单炮偏移过程中，采用OpenMp多线程并行策略．在单炮偏移过程中，首先将震源子波和该炮观测的地震数据进行希尔伯特变换，然后分别进行正演传播，得到炮点端和检波点端的解析波场．对解析波场进行波场分解，得到分解后的上下行波(在本文测试中，波场分解仅实施上下行波分解)．然后采用CLG光学流方法分别计算上下行波场中的传播方向，并将得到的光学流矢量场实施归一化处理．然后采用公式(21)和(20)计算反射张角和方位角．最后采用角度域成像条件提取对应的角度道集．然后将生成的角度道集进行角度插值，避免角度面元化和数值化引起的误差．每个单炮成像道集结果存放在每个处理器附带的局部盘上．把所有炮成像道集数据体收集规约在一起，放到全局盘上，就可以产生多炮角度道集．最后，对角度道集进行必要的后处理，形成最终的结果．

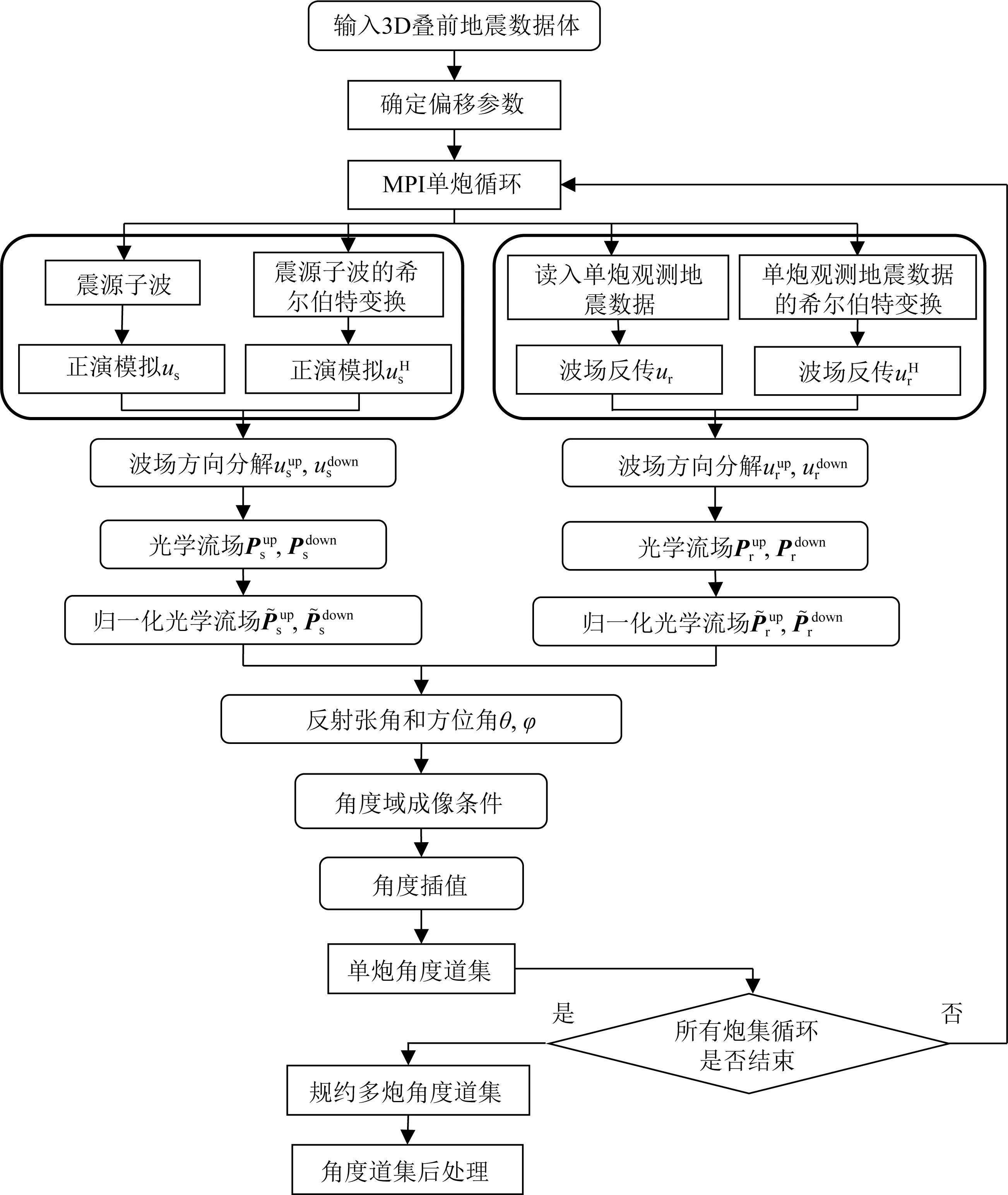
图1 本文提出的基于CLG光学流和波场分解的逆时偏移角度道集方法流程图Fig.1 The flow chart for extracting angle gathers in RTM based on the proposed CLG optical flow method with the wavefield decomposition

图2 水平层状速度模型及相应的波场快照(a) 层状速度模型； (b) 1.0 s时刻的震源端的波场快照； (c) 1.0 s时刻的检波点端的波场快照．Fig.2 The layered velocity model and corresponding wave field snapshot(a) The layered velocity model; (b) The snapshot of the source wavefield at 1.0 s; (c) The snapshot of the receiver wavefield at 1.0 s.

2.1 二维合成数据测试

首先采用层状模型说明本文提出的波场方向估计方法的有效性．其中水平层状速度模型如图2a所示，采用有限差分正演模拟方法生成的震源端波场和检波点端波场快照如图2b和2c所示．在该模型中，反射层深度为1500 m，分析可知只有反射界面附近的波前信息才对反射角道集有效．因此，该区域的波场方向必须被正确的估计．采用不同方法计算的反射界面附近的局部放大的检波点端波场估计的方向如图3所示．其中图3a是坡印廷矢量方法的结果，采用HS和CLG光学流方法估计的波场方向分别如图3b和3c所示．在光学流方法中，考虑到LK方法可能出现奇异现象，因此在本文中，仅对比HS光学流方法和与本文提出的CLG光学流方法．从图3a中可以看出，在大多数区域，采用坡印廷矢量估计的波场方向都是不正确的，波场方向不能被有效的识别，特别是图3a中的红圈所示，该部分的波矢量方向杂乱无章，无法获得正确的波场角度值．坡印廷矢量方法计算的波方向矢量中，有效的波矢量较少，存在较多幅值较小的波方向矢量(图3中，箭头之后线段的长短代表了波矢量的幅值大小)，该部分波矢量无法用于波场方向计算，如图3a中绿圈所示．而HS光学流方法的计算结果则优于坡印廷矢量方法，其中HS光学流方法计算的波矢量幅值比坡印廷矢量方法更加平衡，波矢量方向更加准确．这是因为坡印廷矢量的结果只是对光学流场的初始估计(Zhang，2014)．但是在图3b绿圈所示中，仍然存在较多幅值不均的波方向矢量，导致波场方向估计的精度降低．另外，在图3b中红圈中，杂乱无章的波方向矢量仍然存在，在该区域，计算的波场方向是错误的．对比HS光学流方法和CLG光学流方法，CLG光学流方法能更准确地估计波场方向，特别在图3c中红圈位置，差异更为明显．CLG光学流方法计算的波矢量幅值比HS光学流方法更加平衡(如图3c绿圈所示)，CLG光学流方法可以同时改善估计的方向和幅度．地震波场的方向在一定的范围具有相似性(子波的带限作用)，CLG光学流方法估计的波场方向更具有连续性，更符合地下介质波场传播的特征．其中0～60°角道集叠加的成像结果如图4所示．由于坡印廷矢量方法波场方向不准确，导致在对应的成像剖面中出现了不该出现的大角度的低频噪音．而在HS光流法方法中，低频噪音被有效的去除．但是在大偏移距位置(如图4中白圈所示)，成像结果不聚焦，弥散在成像剖面中．这是由于在该区域，波场的方向计算不准确导致(如图3中所示)．而在本文提出的方法中，成像效果较好，优于HS方法，从而说明了方向估计的有效性．

接下来测试波场方向分解的有效性．图5为采用上下行波波场分解方法得到的检波点端波场快照．图6a为在上行波场(图5a)中应用CLG光学流方法估计的局部波场方向(如图5a中白框所示)．图6b为在下行波场(图5b)中采用CLG光学流方法估计的局部波场方向(如图5b中白框所示)．图6c为在未采用波场分解的检波点端波场中应用CLG光学流方法估计的波场方向(如图2c中白框所示)．可以看到，在图6c中，波形交叉部分(图6c中红圈所示)，仍然存在一些计算错误的波矢量方向．而在波场分解之后，该区域的波场方向得到正确的估计(图6b中红圈所示)，有效提高了波矢量计算的精度，从而说明了波场分解的有效性．另外，图6a中所示的波场方向与炮点端波场方向是相反的，互相关成像结果为大角度的低频噪音，在偏移成像中是需要去除的．因此，采用上下行波分解，可以有效地减少这些噪音的影响．

接下来测试本文提出的角度估计的有效性．图7a为常规除结果．本文提出的最小二乘反演除的结果如图7b所示(图7a和图7b均采用了常规的HS光学流方法计算的波矢量结果来估计反射张角)．由于带限子波的震荡作用，常规方法计算的角度间断、不连续．采用反演的方法估计的角度值更加稳健精确．子波的带限作用引起的角度误差得到有效的消除．

然后采用Sigsbee 2A理论模型说明本文提出方法的有效性．图8a为采用常规的HS光学流方法生成的角度道集，采用本文提出的CLG光学流方法+波场上下行波分解生成的角度道集如图8b所示．可以看出，常规的HS光学流方法的角度道集中含有较多噪声，模糊现象严重，角度道集弥散在比较广的角度中，特别是在盐丘的左侧和上部，成像道集质量比较差．然而在采用本文提出方法的成像道集中，角度道集比较连续、聚焦．对应地0～60°角度道集叠加结果如图9所示．可以明显地看出，采用CLG光学流方法+波场上下行波分解之后的叠加成像中，假象更少，反射轴更加清楚．

在Sigsbee 2A模型上分析不同角度道集生成方法的单炮计算时间，如图10所示．可以看出，坡印廷矢量方法计算效率最高，常规的HS光学流方法次之．而本文提出的CLG光学流方法+波场分解方法需要的计算时间则是最长．这是由于在本文提出的方法中，需要采用解析波场和空间傅里叶变换对外推的波场进行行波方向分解．波场方向分解依赖于解析波场，解析波场需要额外一倍的外推时间．本文的空间傅里叶变换是对整个波场进行分解，不同于局部的波场分解方法(有关局部波场分解方法和常规的波矢量方法的效率对比可参考文献(吴成梁等，2018))，需要的计算量并不大．另外，CLG光学流的计算，最小二乘角度估计，也都需要一定的计算量．对比常规的HS光学流方法和本文提出的方法，本文提出的CLG光学流+波场分解方法的计算效率是常规HS光学流方法的3倍左右．对比成像效果的提升和当前计算机的快速发展，本文认为这些计算代价是值得的．

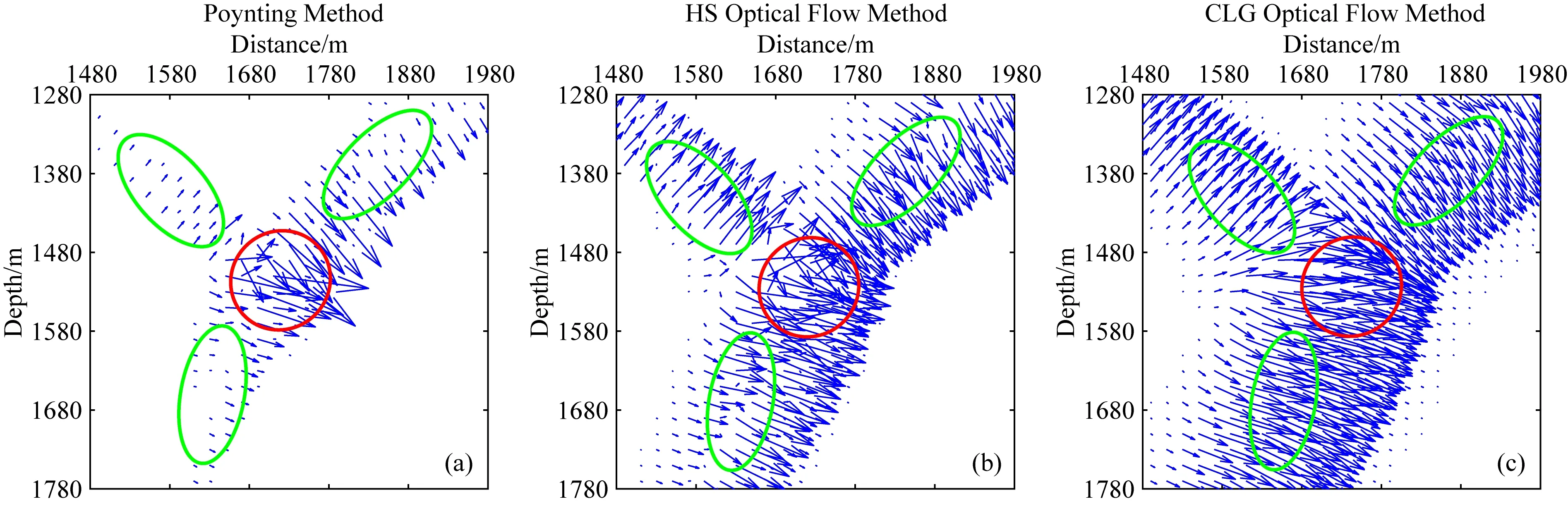
图3 采用不用方法计算的检波点端的波场方向(a) 坡印廷矢量方法； (b) HS 光学流方法； (c) 本文提出的CLG光学流方法．Fig.3 The direction of the receiver wavefield estimated by different methods(a) Poynting vector method; (b) The HS optical flow method; (c) The proposed CLG optical flow method.

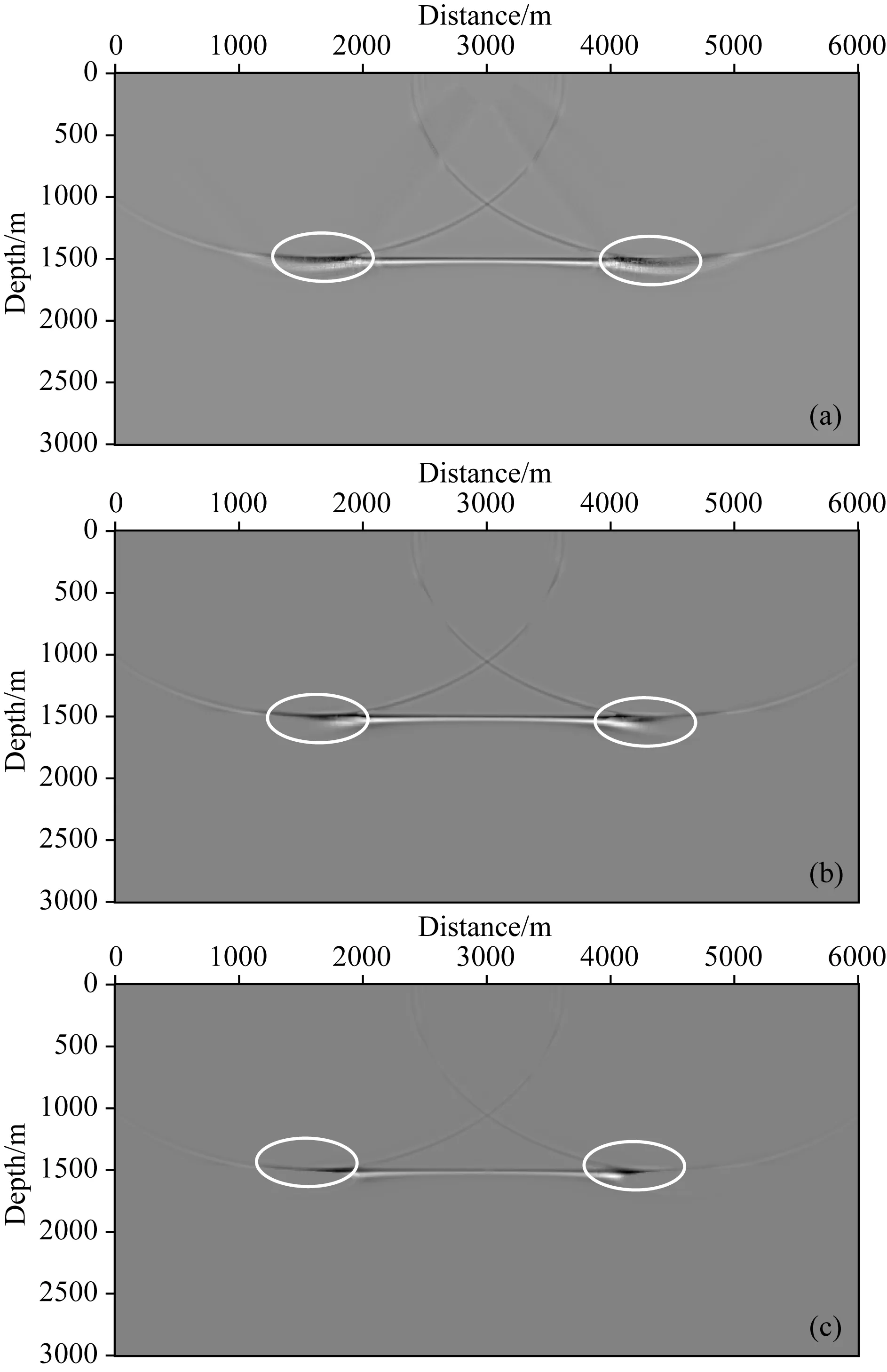
图4 0～60°角度道集叠加结果(a) 坡印廷矢量方法； (b) HS 光学流方法； (c) 本文提出的CLG光学流方法．Fig.4 The imaging results stacking by the 0～60°angle gathers(a) Poynting vector method; (b) The HS optical flow method; (c) The proposed CLG optical flow method.

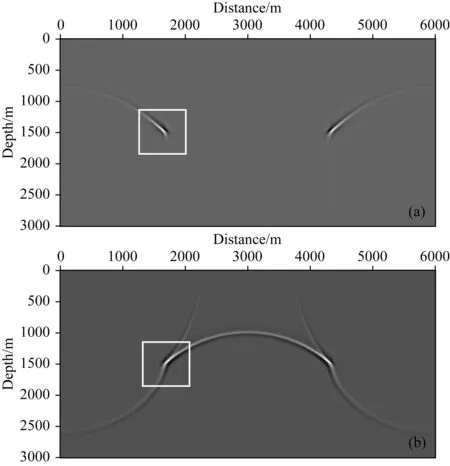
图5 采用上下行波分解方法之后的检波点端的波场快照(1.0 s时刻)(a) 上行波波场快照； (b) 下行波波场快照．Fig.5 The receiver wavefield with the wavefield decomposition method at 1.0 s(a) The upgoing wavefield; (b) The downgoing wavefield.

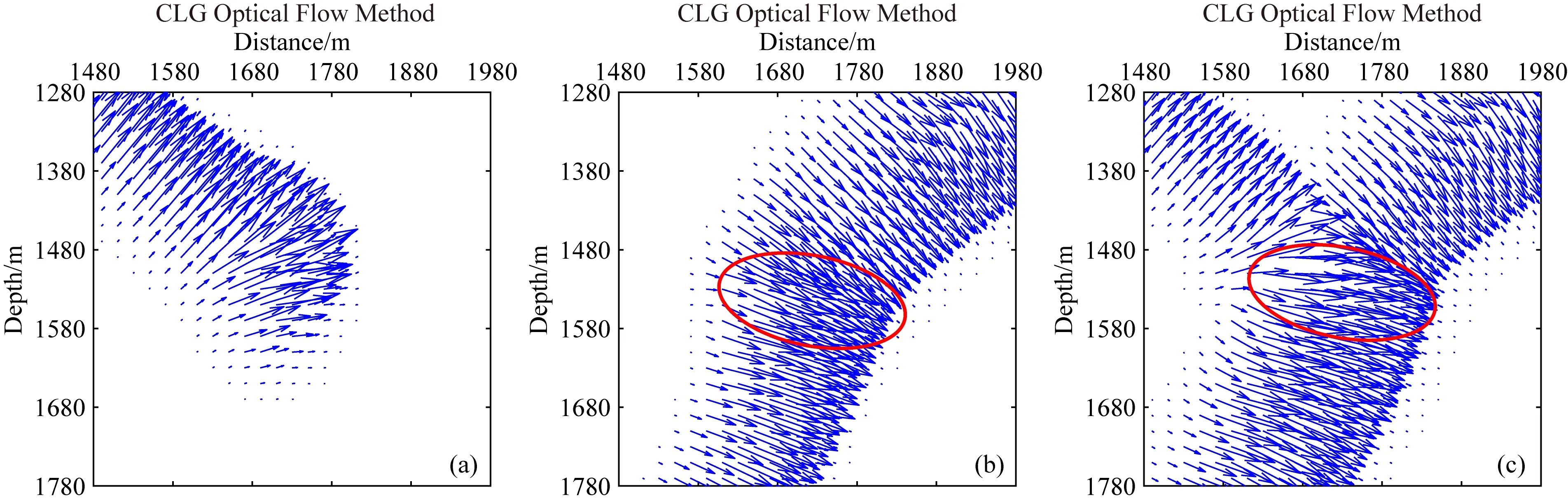
图6 采用CLG光学流方法计算的检波点端的波场方向(a) 采用上行波波场计算的波场方向； (b) 采用下行波波场计算的波场方向； (c) 未采用波场分解方法计算的波场方向．Fig.6 The direction of the receiver wavefield estimated by the proposed CLG optical flow method(a) With the upgoing wavefield; (b) With the downgoing wavefield; (c) Without the wavefield decomposition.

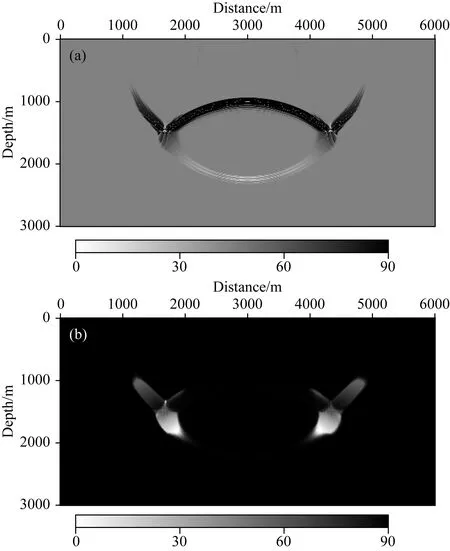
图7 层状模型中估计的反射张角结果(a) 常规的方法； (b) 本文提出的最小二乘除方法．Fig.7 The estimated reflection angle in the layered model by (a) conventional method and (b) the proposed least square division method

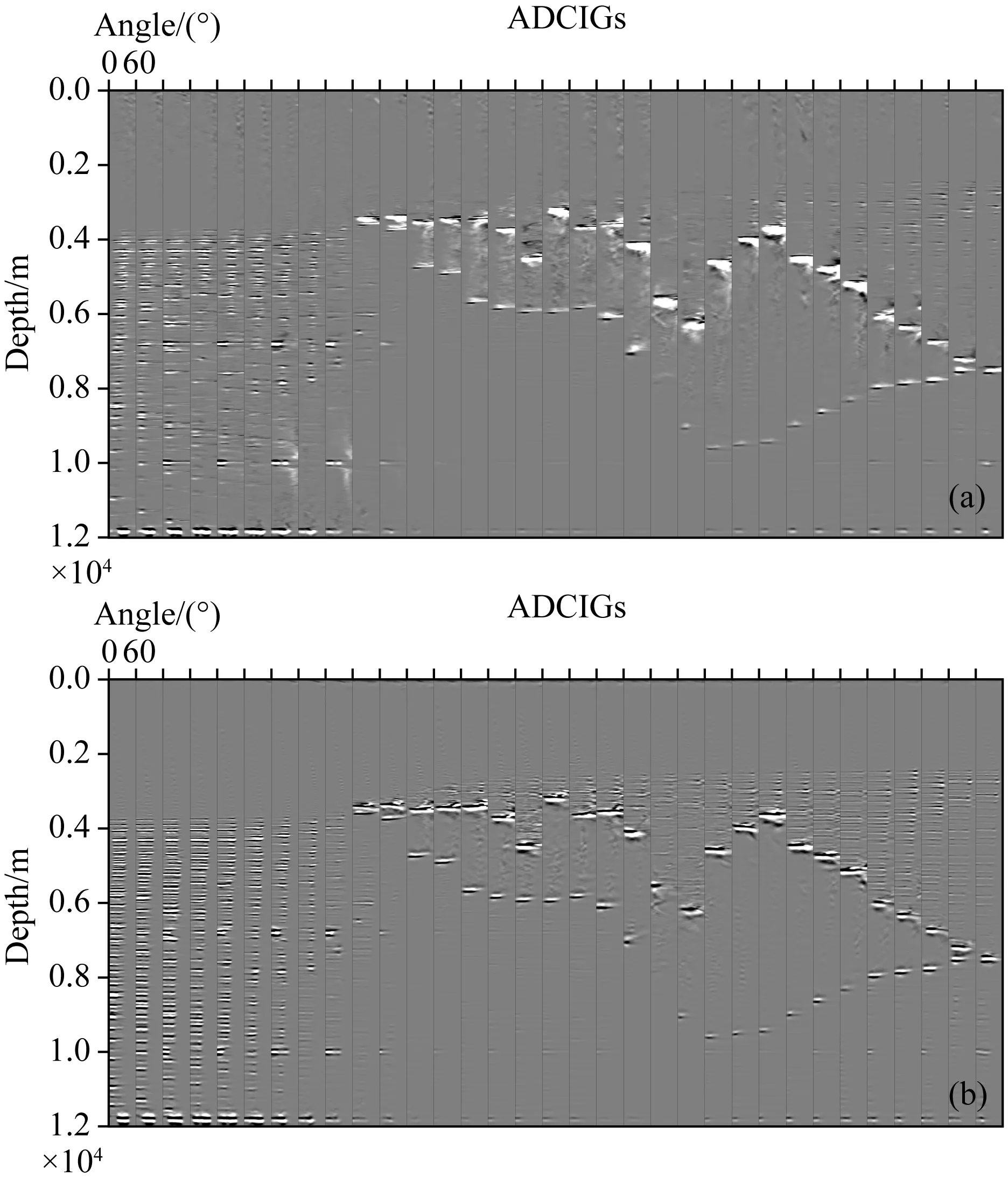
图8 Sigsbee 2A模型每隔100个CDP点提取的角度道集(角度范围0～60°，角度间隔1°)(a) 常规的HS光学流方法； (b) 本文提出的CLG光学流+波场分解方法．Fig.8 The ADCIGs of Sigsbee 2A model. The ADCIGs is selected with a 100-CDP interval and the angle range is 0～60 degrees with a 1 degree interval(a) The conventional HS optical flow method; (b) The proposed CLG optical flow method with the wavefield decomposition.

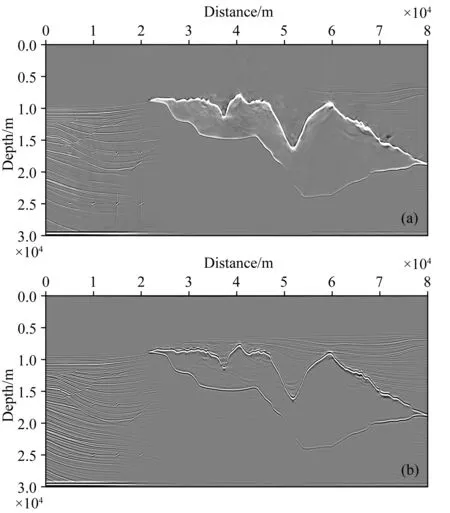
图9 Sigsbee 2A模型0～60°角度道集叠加结果(a) 常规的HS光学流方法； (b) 本文提出的CLG光学流+波场分解方法．Fig.9 The stacked image of Sigsbee 2A model by ADCIGs. (The angle range is 0～60 degrees)(a) The conventional HS optical flow method; (b) The proposed CLG optical flow method with the wavefield decomposition.

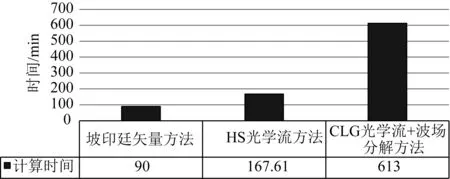
图10 采用不同方法计算的单炮时间对比Fig.10 Comparison of single shot time calculated by different methods

2.2 二维实际资料测试

接下来，采用某地区陆上实际资料说明本文提出方法的有效性．其中图11a为常规的HS光学流方法生成的角度道集，图11b为本文提出的方法生成的角度道集．对比可以看出，采用本文提出方法生成的角度道集假象比较少，成像道集比较聚焦．另外，从叠加成像结果(图12)可以看出，常规的光学流方法结果中，存在较多的偏移假象，叠加剖面比较模糊，反射波同相轴不连续．在本文提出的方法中，成像结果连续性较好，剖面噪声和偏移假象较少，成像质量结果明显好于常规的光学流方法．

图11 陆上某地区2D实际资料，每隔100个CDP点提取的角度道集(角度范围0～60°，角度间隔1°)(a) 常规的HS光学流方法； (b) 本文提出的CLG光学流+波场分解方法．Fig.11 The ADCIGs of real data. The ADCIGs is selected with a 100-CDP interval and the angle range is 0～60 degrees with a 1 degree interval (a) The conventional HS optical flow method; (b) The proposed CLG optical flow method with the wavefield decomposition.

3 讨论与结论

利用波动方程的时间演化进行波矢量方向计算在逆时偏移角度道集中是一个核心内容．局部波场分解方法能够处理复杂波场，传播方向计算准确，但是效率低下，无法在大规模的3D逆时偏移角度道集中实用化．坡印廷矢量方法可以用于计算波场传播方向，该方法计算简单，计算效率高，适合并行处理，但是坡印廷矢量通常会出现不稳定情况，在波场复杂情况时，波场方向估计不准确．

光学流方法可以提高波场方向估计的精度．光学流方程本身是欠定的，需要引入额外的约束计算光学流场．通过假设在局部邻域Ω内光学流矢量是不变的，LK光学流方法构建局部的线性方程组计算方向矢量．然而，LK光学流方法依赖于局部点的梯度值，容易出现奇异现象．全局HS光学流方法通过引入全局的能量约束，能够比较稳定地求解光学流场，但是在该方法中，距离计算点较远区域的波场也会参与到当前点的计算中，导致计算的波场方向精度有所下降．本文采用CLG光学流方法计算波场方向，在施加全局约束的基础上，考虑局部点的加权作用，在保持波场方向估计稳定的基础上，提高波场方向计算精度．该方法简单高效，便于并行处理，其迭代格式与HS光学流方法相同，几乎没有太多的额外计算量，非常适合大规模地震数据处理．

为了克服光学流方法无法处理波前重叠问题，本文利用解析波场对波场进行方向分解来减弱这种影响．通过构建解析波场，仅需波场的空间傅里叶变换即可实现任意波场方向分解，有效地避免了逆时偏移外推过程存储波场问题，减少了内存和硬盘使用．理论上可以通过波数域滤波提取任意方向的波场，但是考虑到计算量问题以及地下介质的特征主要以层状沉积层加上大、小尺度的速度异常体，本文的数值实验仅考虑了上下行波分解情况．针对不同的地质构造特征，可以任选几个方向角度进行分解，波场分解的角度需要根据地质特征确定．方向分解个数越多，波前交叉分的更仔细，但是需要的计算量越大．波场分解的个数需要在计算量和效果中达到平衡．

图12 陆上某地区2D实际资料，0～60°角度道集叠加结果(a) 常规的HS光学流方法； (b) 本文提出的CLG光学流+波场分解方法．Fig.12 The stacked image of real data by ADCIGs. (The angle range is 0～60 degrees)(a) The conventional HS optical flow method; (b) The proposed CLG optical flow method with the wavefield decomposition.

进一步地，本文提出采用有效的归一化方法和最小二乘除方法，提高反射角的估计精度，有效避免带限波场引起的震荡作用．并对角度道集进行了面元化和规整化处理，以获得高质量的角度道集．理论和实际资料证明了本文提出方法的有效性．

致谢感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中石化物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持．感谢审稿人提供的宝贵建议．

附录A：CLG光学流控制方程推导

(A1)

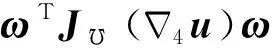
(A2)

重新整理，误差泛函ECLG(ω)可表示为

(A3)

采用变分法，上式误差泛函对应的Euler-Lagrange方程的解为

(A4)

最后，得到CLG光学流控制方程为

(A5)

其中Δ为拉普拉斯算子．