有限导电内核的驱动方式对发电机模型的影响
丁嘉威, 王正涛,2*, 詹文臻, 刘美琴
1 武汉大学测绘学院, 武汉 430079 2 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
0 引言
行星的磁流体内核的流体动力学模拟主要是通过求解包括科里奥利力在内的Navier-Stokes方程,并结合Boussinesq近似下的磁流体动力学(MHD)感应方程、温度(或熵)方程与化学成分(本文未考虑)方程来实现的,得益于数值算法的不断改进以及高性能计算机的发展,使得当前发电机模型的数值模拟计算速度越来越快,描述各物理量的参数越来越多且日益接近真实值.
1995年,超级计算机Cray C90上成功模拟了一个包含有限导电内核的三维自恰地球发电机模型(Glatzmaier and Roberts, 1995a),同年又模拟了长达4万年的地球磁场,并成功实现了磁场的翻转(Glatzmaier and Roberts, 1995b).此后相关研究者们在以上基础上对发电机模型中的物理参数进行修改或增加、或使用更为合理的物理参数及数值方法来得到新的发电机模型并进行系统性的研究(Christensen et al., 1998; Christensen et al., 1999; Olson et al., 1999; Christensen et al., 2001; Kutzner and Christensen, 2002; Takahashi et al., 2007; Takahashi et al., 2008; Wicht, 2014; Matsui et al., 2016).地球内核的超速旋转现象的发现(Song and Richards, 1996),利用地震得到的地球内核表面的镶嵌结构(Krasnoshchekov et al., 2005),地核条件下铁、固态铁和铁硅混合物的导热性和导电性(Pozzo et al., 2012, 2014),利用高压试验和三维x射线显微层析成像技术推断的核-幔边界处的温度数据(Nomura et al., 2014),通过数值模拟分析得到的深内部地球结构对内核平动振荡本征周期的影响(江颖等, 2014),关于核幔耦合对地球自由核章动的激发影响(崔小明等, 2018)等各类更精细的地球内部数据或相关研究都为更真实的地球(磁流体)发电机模型提供了很好的数据条件.
对于内核在发电机中的作用,Hollerbach和Jones(1993)关于内核对地磁场波动和翻转的作用进行了研究;Glatzmaier 和Roberts(1995b)提出了包含有限导电内核的三维、自恰地球发电机模型,并成功实现了主磁场的翻转;Wicht(2002)研究分析了有限导电内核对地磁场翻转频率的影响,并详细描述了引入内核后的发电机方程;Reshetnyak(2016)研究了半径不断增大的内核在发电机中的作用.而关于内核在外核驱动下的高转速(通常每时间尺度达几百弧度)、大波动的问题,可以通过引入引力耦合来稳定内核的转速(Aubert and Dumberry, 2011).需要注意的是此处的高转速、大波动是以惯性系为参考进行描述的,而并非以外核系统作为参考.
本文以Takahashi等(2007, 2008)所提出的两种数值发电机模型为基准,研究有限导电内核在两种旋转方式下对发电机模型的极向和环向动能、极向和环向磁能、核-幔边界处的磁场强度、磁雷诺数、磁极翻转频率、轴向偶极子强度、赤道对称性、纬向性和磁通量集中度的影响,其中后四者用于研究类地发电机的成立条件时所用的四种参数(Christensen et al., 2010).
1 基本原理
通常,对于磁流体发电机模型的求解会从描述流体运动的Navier-Stokes方程出发:
(1)
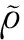
最终得到其无量纲形式为:
(2)
其中p″为修正后的压力项,ez为旋转轴方向的单位矢量.无量纲参数的具体表达式分别为:
埃克曼数
(3)
瑞利数
(4)
普朗特数
(5)
磁普朗特数
(6)
式中,下标“o”表示外核边界处的相应物理值,“i”表示内核边界处的相应物理值,d为外核厚度,ΔT为内外核温度差,κ为热扩散率.
最后,将方程(2)与以下方程联立:
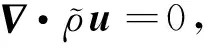
(7)
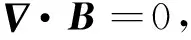
(8)
(9)
(10)
即得到求解发电机模型的无量纲方程组.
将有限导电的内核引入发电机模型后,内核和外核的发电机方程就必须同时进行求解,它们由磁场和水平电场的连续性来关联:
B=Bi,r=ri;
EH=EHi,r=ri.
(11)
若内核在外核的驱动下发生转动,则其驱动力包含洛伦兹力与黏性力.转速可由角动量方程进行描述,其具体表达式为:
(12)
其中I是沿Z轴旋转的内核转动惯量,ωi为内核旋转角速度,ΓL、Γv分别对应于洛伦兹力及黏性力.内核为导电的情况下,其对应的发电机方程为:
(13)
在以上基础上通过更改地球内核的电导率、旋转方式来研究其对主磁场带来的影响.
2 模型参数
2.1 基准模型
本文选择使用了Takahashi等(2007)用于研究磁极转换所使用的模型及Takahashi等(2008)所提出的数值发电机中埃克曼数为2×10-5的模型作为基准模型,分别简称为FT07和FT08,模型中的球谐展开阶次为16阶,径向的切比雪夫多项式的展开项数为32,时间尺度方案选择了黏性扩散时间,其具体转换方法即前文对时间t的变量代换.
模型FT07所对应的物理参数为:E=1×10-5,Ra=8×107,Pm=0.5,Pr=1;模型FT08所对应的物理参数为:E=2×10-5,Ra=2×107,Pm=1.5,Pr=1.
对于内核电导率,基准模型将其设定为绝缘,且与外核之间不存在任何相关物理作用的.
本文默认所有内核的密度均等于外核密度.
所有模型所对应的内核的机械边界条件选择使用刚性、不可穿透的边界,这与真实的内核-外核边界物理上最为接近.
内核的热边界条件默认均为固定熵条件,即熵si=sbottom.
2.2 由外核驱动旋转的有限导电内核模型(DOC, Driven by Outer Core)
包含有限导电内核的模型的无量纲参数、内核密度、内核的机械边界条件以及热边界条件均与进行比对的相应基准模型保持一致,且内核的电导率均认为与外核相同(目前内核的增长通常被认为是外核物质在内核边界上凝固的结果,因此认为内核电导率和外核电导率相同在物理上解释可能更为合理).
此模型下,内核旋转被认为是洛伦兹力和黏滞力共同作用下的结果.
2.3 固定旋转速度的有限导电内核的模型I(FSR I, Fixed Super Rotation I)
该模型的转速使用对应的DOC模型在相应时间尺度内的最大转速.分别对应于351.06rad/时间尺度和383.96rad/时间尺度.
需要注意的是,此模型下的内核不会与外核存在任何有关力的作用,即认为内核是自发旋转、不受外核影响的.
2.4 固定旋转速度的有限导电内核的模型II(FSR II, Fixed Super Rotation II)
此模型与FSR I的区别仅在于内核的转速不同,所使用的转速为所对应的DOC模型在对应时间尺度下的内核平均转速,分别为:32.90rad/时间尺度和-22.68rad/时间尺度.
2.5 固定旋转速度的有限导电内核的模型III(FSR III, Fixed Super Rotation III)
与FSR II类似,其转速对应为:-296.69rad/时间尺度和-363.98rad/时间尺度.
3 模型间的比较分析
3.1 核-幔边界处的磁场强度
核-幔边界处的磁场强度通常使用埃尔泽塞尔数进行描述:
(14)
其大小等于无量纲磁场强度的平方,该数也可以用于描述洛伦兹力与科里奥利力的比值.式中下标rms表均方根.
根据图1可以看出模型FT07及其对应的几种比对模型的磁场强度在0.4个时间尺度后基本在0.3左右上下波动,因此对于模型FT07,其所有的对比均使用0.4~3个时间尺度内的数据.同理根据图2,FT08使用0.5~3个时间尺度内的数据.
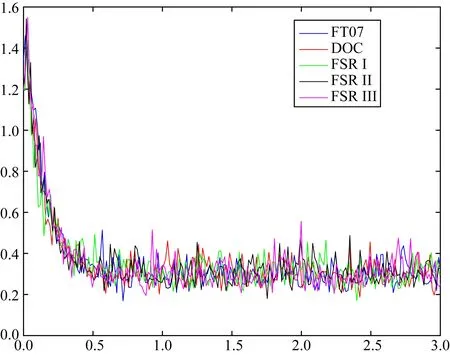
图1 模型FT07及其对应的DOC、FSR I、FSR II、FSR III的核-幔边界处的磁场强度.该模型所使用的积分时间步长的数量级达10-6,造成了原图曲线存在大量重叠的情况,因此此处每隔5000个点取一个来绘制其趋势,计算时仍采用全部数据.后作类似处理的图像会标注相应的间隔,如“(5000)”Fig.1 Magnetic field intensity at core-mantle boundary of benchmark dynamo FT07 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III. Order of magnitude of integral time step used in this model is up to 10-6, which causes a large amount of overlap in the original graph curve. Therefore, here every 5000 points are taken to plot its trend, but all data are still used in the calculation. Images processed similarly are marked with corresponding intervals, for example,“(5000)”
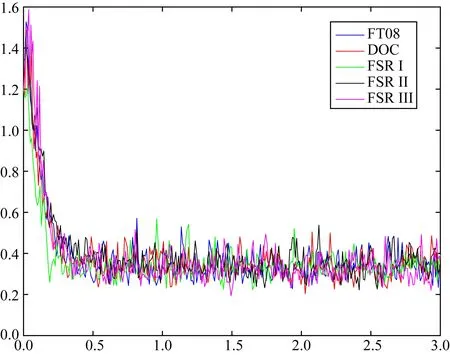
图2 模型FT08及其对应的DOC、FSR I、FSR II、FSR III的核-幔边界处的磁场强度(5000)Fig.2 Magnetic field intensity at core-mantle boundary of benchmark dynamo FT08 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)
3.2 DOC模型转速
内核转速可由角动量方程(12)进行描述.计算得到的转速图见图3—4.
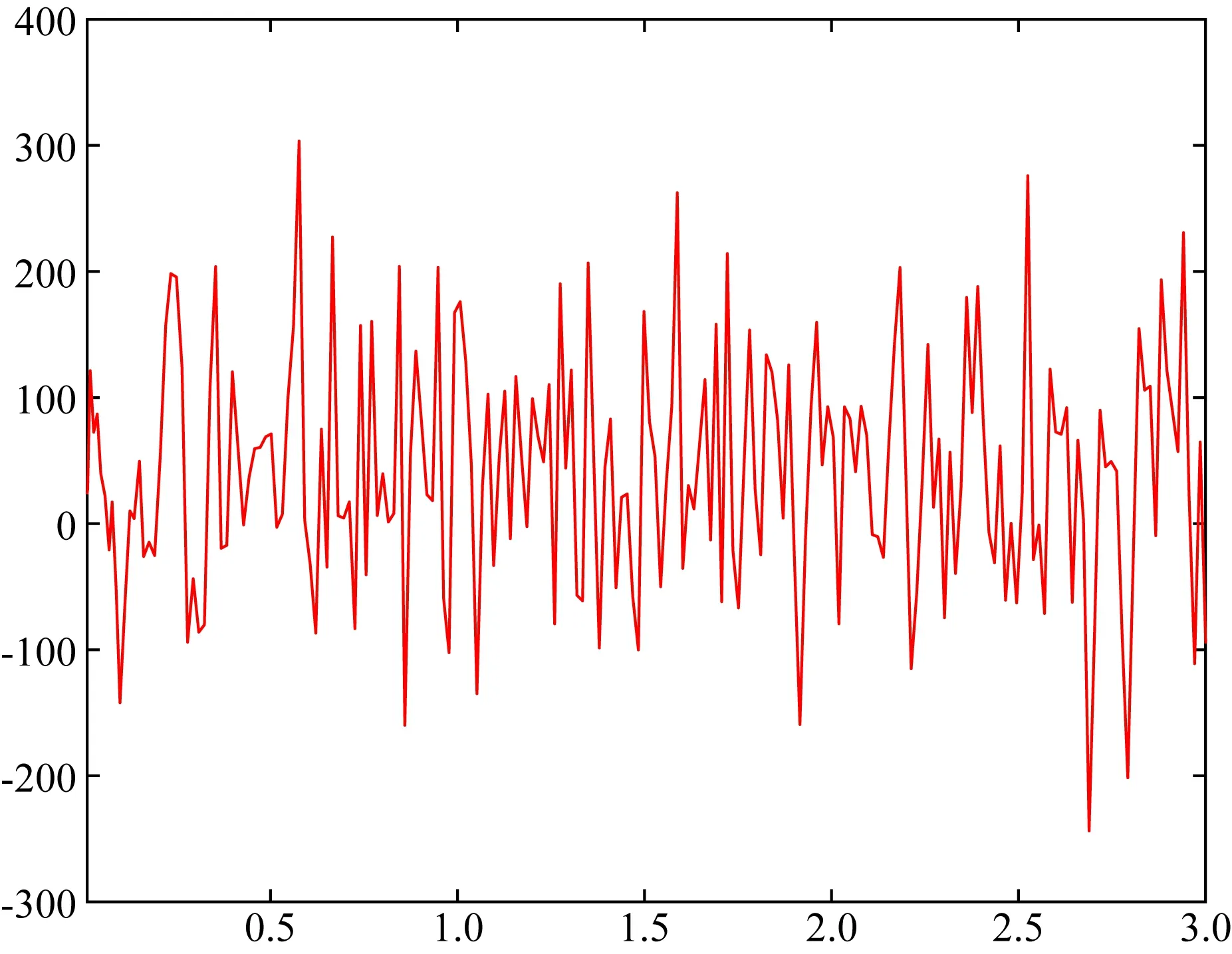
图3 模型FT07所对应的DOC模型在0.01~3个时间尺度内的内核转速(5000)Fig.3 Inner-core rotation speed of the DOC model corresponding to model FT07 in 0.01~3 timescales (5000)
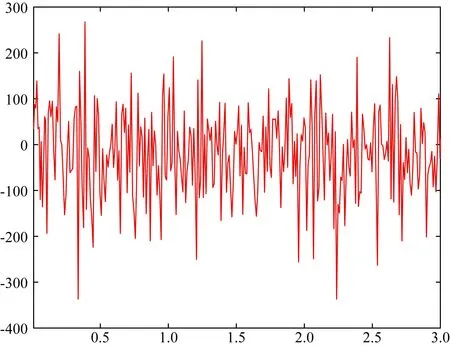
图4 模型FT08所对应的DOC模型在0.01~3个时间尺度内的内核转速(5000)Fig.4 Inner-core rotation speed of the DOC model corresponding to model FT08 in 0.01~3 timescales (5000)
3.3 外核能量
通过比较外核的动能、磁能以及相应的磁场变化来研究不同驱动方式下的内核对数值发电机作用的影响.在螺线向量场在球坐标系下的分析中通常会对其应用极向-环向分解,是亥姆霍兹分解的一个受限制的形式,在本文所涉及的问题中,动能和磁能具体的极向-环向分解后表达形式分别为:
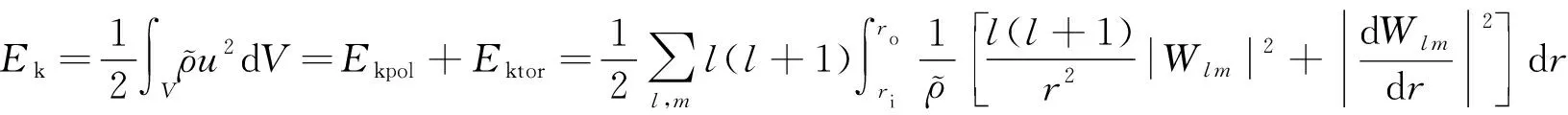
(15)
(16)
式中,Wl m为动力场极向位能,Zl m为动力场环向位能,bl m为磁场极向位能,jl m为磁场环向位能.
3.4 磁雷诺数
磁雷诺数的定义为:
(17)
主要用于描述磁流体内部速度u和磁场B的方均根值的比值.
3.5 磁极翻转频率
磁极翻转频率f可根据磁极纬度的变化次数统计得到.
3.6 轴向偶极子强度
本文中轴向偶极子强度定义为偶极子(axial dipole,AD)与非偶极子(non-axial dipole,NAD)之比:
(18)
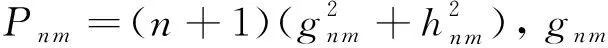
3.7 赤道对称性
对于赤道对称性,通常使用奇偶比O/E进行描述,即2到8阶的调和级数在核-幔边界处的阶次和(n+m)为奇数的分量和与阶次和为偶数的分量和之比.
3.8 纬向性
纬向性即纬向-非纬向比Z/NZ是核-幔边界处所有纬向性分量和非纬向性分量之比.
3.9 磁通量集中度
核-幔边界处的磁通量在一定程度上集中并形成了强辐向场斑块Br,可用通量集中因子FCF来定量描述:
(19)
其中〈〉表示在整个球面上求平均.
3.10 比较分析
表1给出了包含导电内核的各发电机模型的各物理量较基准模型的变化量.可以看出,有限导电内核的引入对模型的磁场强度只会产生最高不到4%的变化,极、环向动能最高仅约2%,极、环向磁能最高也约为4%,磁雷诺数的变化量不到1%,磁通量强度最高约5%.但对于轴向偶极子强度和磁极翻转频率,各模型相较基准模型的变化量则存在较大差异,特别的,DOC模型对于磁极翻转频率几乎没有影响;对于赤道对称性,除以FT07为基准的FSR I的变化量达到+19.03%之外,其他的变化量均小于6%;在纬向性的比较中,除了以FT07为基准的FSR II和FSR III的变化量达17%以上,其他模型的变化量均在10%以下.
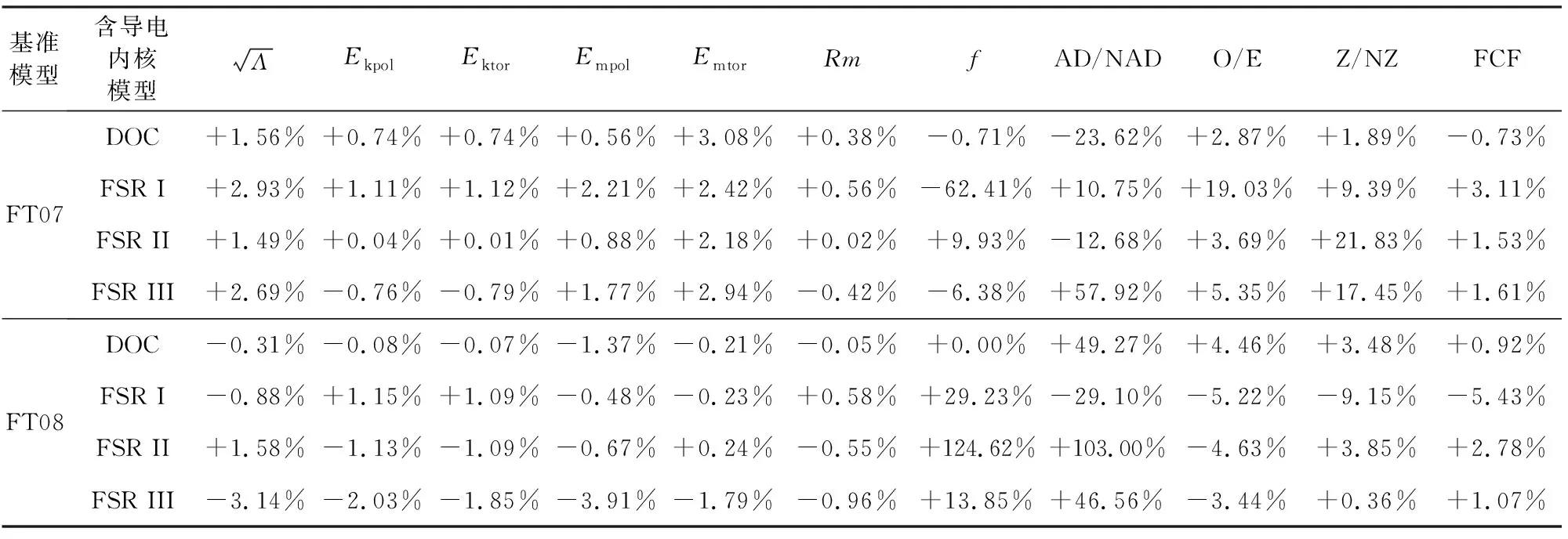
表1 各模型对应的各物理量较基准模型的变化量Table 1 Variation of each physical quantity corresponding to each model compared with the benchmark dynamo
4 结论
有限导电内核的引入,对于模型的磁场强度、极向和环向动能、极向和环向磁能、磁雷诺数和磁通量集中度的影响是极弱的,只会产生小于6%的变化量.这可能是由于内核本身的能量相对于外核来说是极小的,因此引入有限导电的内核后,其所带来的影响也应不会明显.
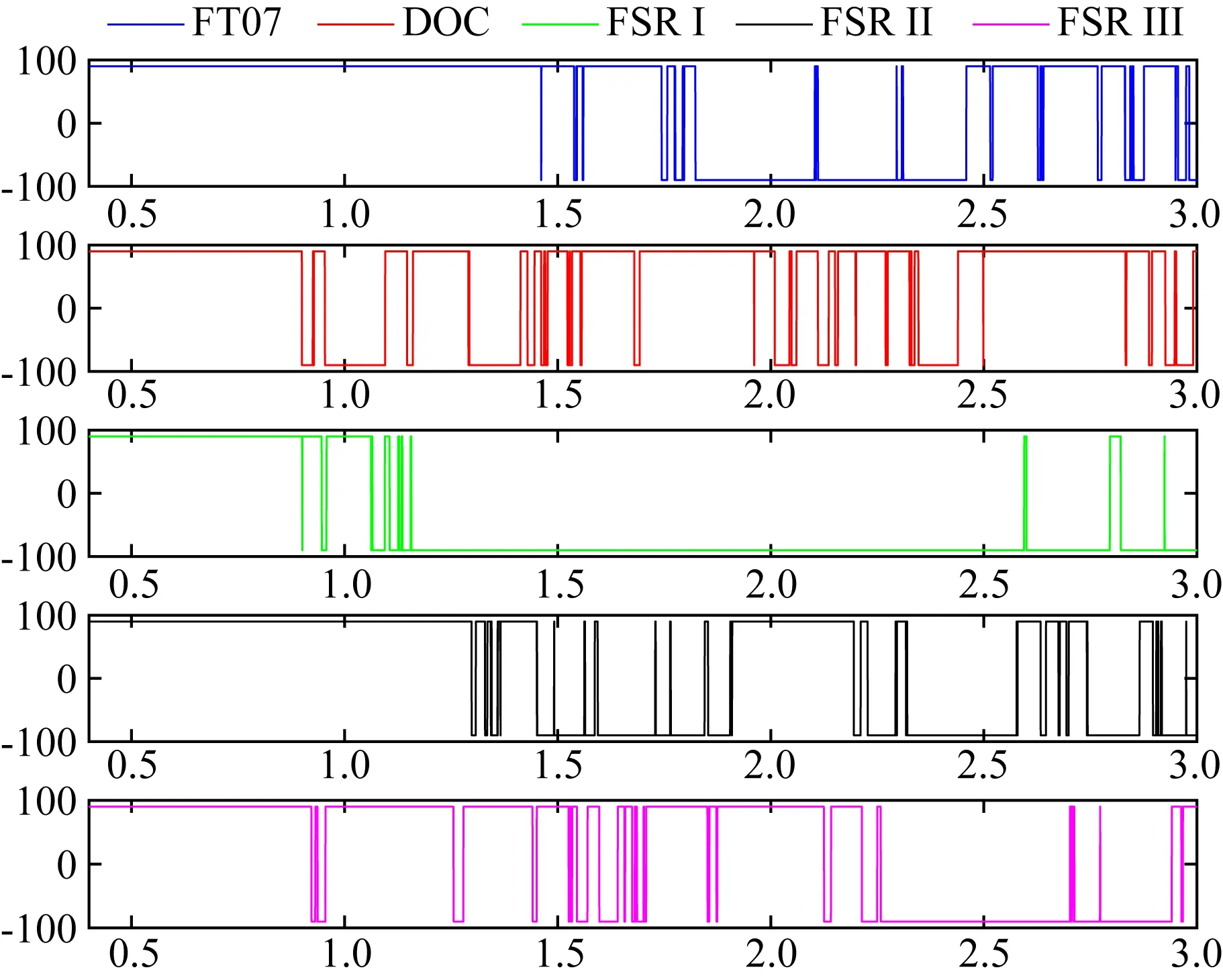
图5 模型FT07及其对应的DOC、FSR I、FSR II、FSR III的磁极纬度Fig.5 Latitude of magnetic pole of benchmark dynamo FT07 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)
对于轴向偶极子强度,由于本文所使用的模型是可以实现磁场翻转的发电机模型,而这类模型的轴向偶极子强度通常都较弱,其本身基数较小,因此引入有限导电内核后,导致其相对变化量较大,但其最大绝对变化量小于0.03,且结合图5—8,可以明显看出,有限导电内核对轴向偶极子强度的影响更多的集中在磁极翻转的时刻,这表明对于那些偶极性较弱的发电机模型,有限导电内核的引入与否会直接影响该发电机的偶极子强度,并且对于可实现磁场翻转的发电机模型来说,这一影响可能会更明显.
而对于赤道对称性和纬向性,除部分模型存在较大的变化外,其余模型的影响均小于10%,若发电机模型涉及以上两个物理量,有限导电内核(FSR)仍是值得考虑的因素.
对于翻转频率来说,DOC模型的翻转次数与基准模型几乎完全一致,而FSR模型则对翻转频率造成了不同程度的较明显的影响.这表明DOC模型的内核旋转虽然波动大、转速高,但可能由于其驱动
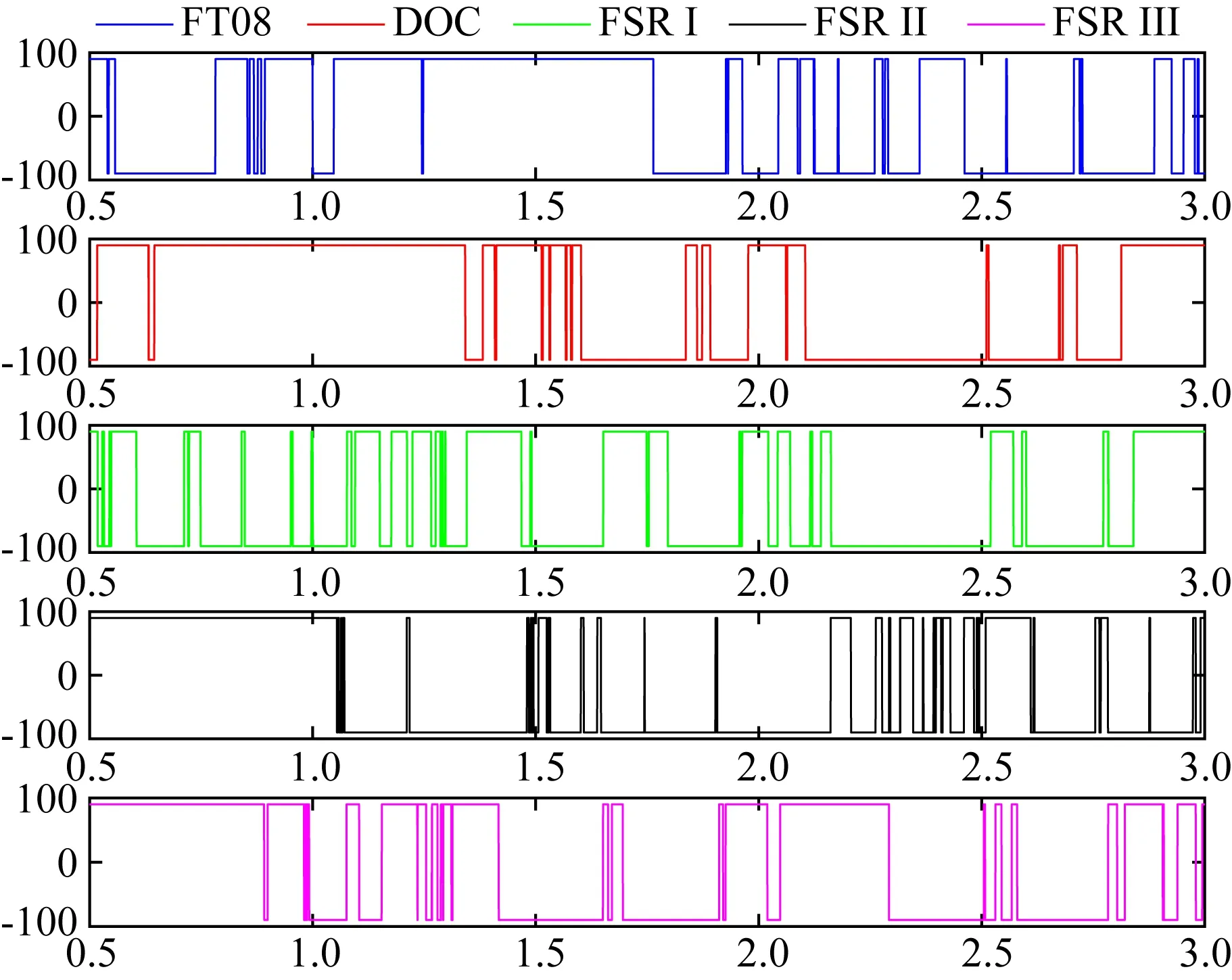
图6 模型FT08及其对应的DOC、FSR I、FSR II、FSR III的磁极纬度Fig.6 Latitude of magnetic pole of benchmark dynamo FT08 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)
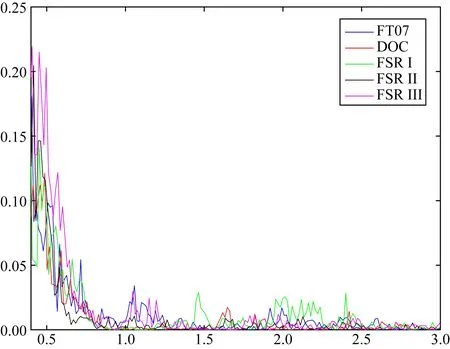
图7 模型FT07及其对应的DOC、FSR I、FSR II、FSR III的轴向偶极子强度(5000)Fig.7 Relative axial dipole power of benchmark dynamo FT07 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)
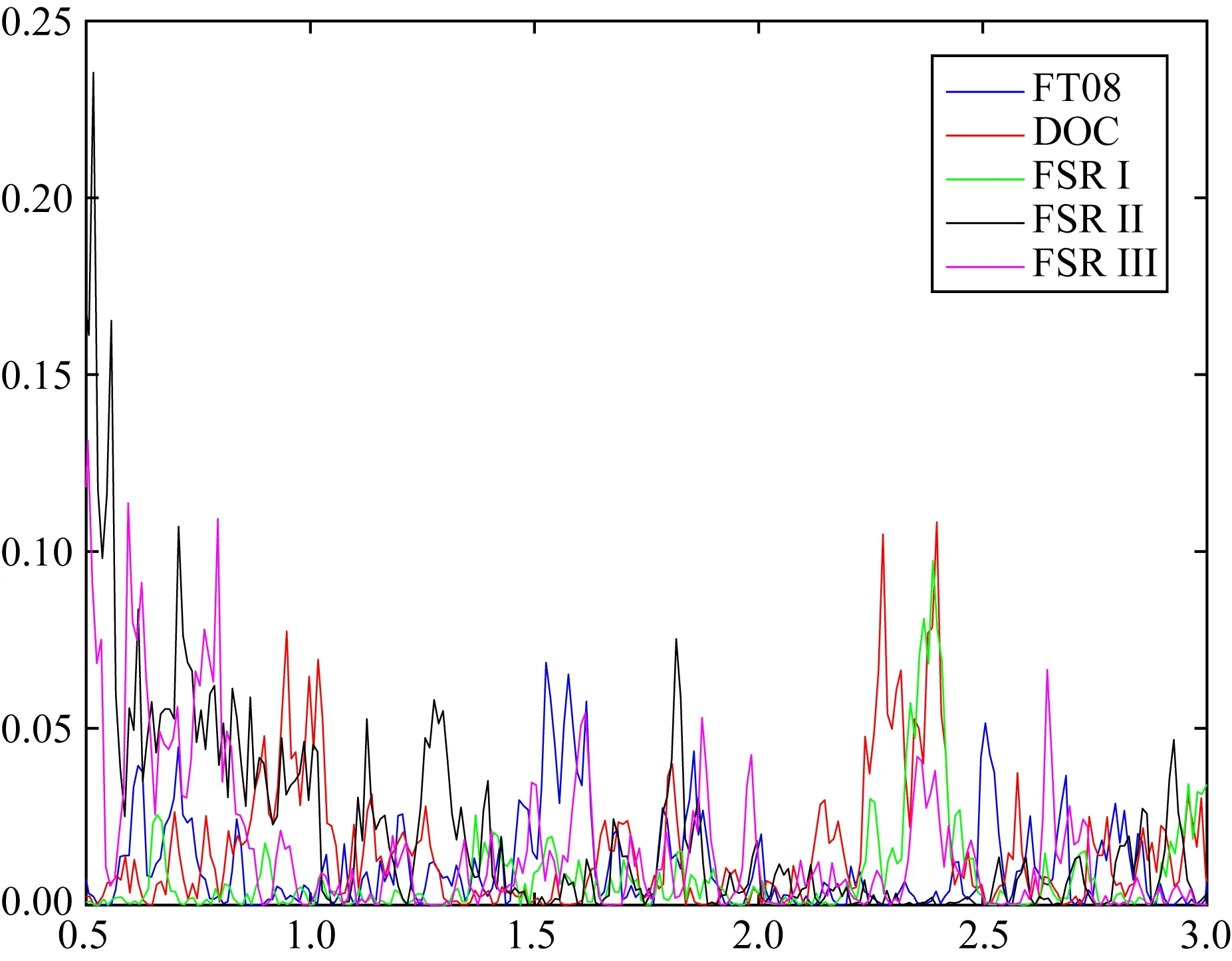
图8 模型FT08及其对应的DOC、FSR I、FSR II、FSR III的轴向偶极子强度(5000)Fig.8 Relative axial dipole power of benchmark dynamo FT08 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)
方式及机理与真实情况相近且考虑到内核本身的能量对外核产生的影响程度有限,因此DOC模型与基准模型的翻转频率几乎完全一致也在物理上更为合理;而对于FSR模型,其本身就是一种为了方便控制转速而理想化后的模型,因此其内核可能会对外核磁流体产生一定影响,而引起磁极翻转频率发生较明显变化.
总体来说,本文中的DOC模型除偶极性以外,对于其他物理量所能带来的变化都是可忽略的,且考虑到实际内核较外核的能量比来说,以上结果是较合理的.
致谢MagIC开发团队提供的球壳中的流体动力学数值代码MagIC、南方科技大学林玉峰副教授提供的理论指导及武汉大学超算中心提供的算力支持.

