共转换点道集S变换谱相似性的多波地震数据横波波场提取技术
黄德智, 韩立国*, 杨飞龙, 李辉峰, 苑强, 孙楠, 杨文平
1 吉林大学地球探测科学与技术学院, 长春 130026 2 西安石油大学地球科学与工程学院, 西安 710065 3 中石化石油工程地球物理有限公司华北分公司, 郑州 450000 4 中国石化东北油气分公司勘探开发研究院, 长春 130062
0 引言
相比常规地震数据,多波地震数据记录了更多地质属性信息,为地质构造的解释和研究提供了更多参考依据.多波地震勘探中,因多分量检波器的接收方向与各分量地震波的振动方向存在角度,造成各分量地震波在其他分量上产生投影,使其自身产生振幅损失(魏建新和狄帮让,2005);与此同时,这种投影也对各分量地震信号的成像产生干扰,尤其是投影至横波分量中的纵波信号会对横波分量中的横波信号成像产生严重干扰.因此在多波地震数据成像前,需对数据做纵、横波场分离处理.
多波地震数据的纵、横波分离,主要依据地震波的运动学特征(波的速度、振动方向)和动力学特征(波的振幅、频率、相位)等进行分离,分离方法主要有F-K滤波、τ-p变换、Radon变换、极化滤波、全波形反演、散度和旋度等.Radon变换和τ-p变换将纵波和横波在变换域中收敛到不同“点”上,通过切除噪声或干扰区域的方法分离纵、横波波场.Stoffa和Treitel先后提出平面波分解的Radon变化方法(Stoffa et al.,1981;Treite et al.,1982);Beylkin(1987)用最小平方反演法实现Radon变换离散化;魏修成等(1993)用空间坐标域与视慢度之间的变换关系给出了三种(τ-p、F-K、离散拉冬变换DRT)变速视慢度波场分离方法;包军强等(1998)用τ-p变换法、门槛值调节和圈闭靶区对浅层多波进行了分离与提取;罗省贤和李录明(1999)利用多波资料的动力学和运动学特征在F-K域实现多波炮集记录变速波场分离;孙显义(2002)用τ-q变换将不同层位反射波聚焦成“点”进行波场分离.在极化滤波分离波场方面,Shimshoni和Smith(1964)用垂直分量和水平分量的时间平均矢量积,根据不同分量间的相位关系从背景噪声中提取有效信号;Dankbaar(1985)根据近地表速度与检波器组合特性设计滤波器,在F-K域内实现理论数据的纵、横波场分离;李锦飞和李人厚(1998)用小波分析多波数据的时频域特性和空间运动特性,构造滤波函数实现波场分离;张玉芬和周建新(1999)对影响空间方向滤波的因素进行了分析;张国毅和刘永坦(2000)提出了实数加权极化变换法;胡天跃等(2004)根据慢度和极化特征,用最小方差约束法重构了纵、横波波场.Devaney和Oristaglio(1986)提出平面波分解法分离纵、横波;张关泉和周洪波(1995)基于弹性波波动方程推导出了纵横波波场分离公式;马德堂和朱光明(2003)给出完全弹性波波动方程的等价方程, 用伪谱法求解得到纯纵波或纯横波波场;陈可洋等(2009)给出等价二阶弹性波动方程,应用高阶交错网格有限差分法求解得到理论数据的纯纵、横波场.Dellinger和Etgen(1990)提出在F-X域内基于散度和旋度滤波因子,对各向异性的纵波和横波进行分离;Sun等(2004)提出了相位相关法,基于有限差分弹性波波动方程混合向下外推法,通过控制散度和旋度,对弹性波波场分离进行了数值模拟;黄少华等(2019)在模型数据中应用多震源弹性波全波形反演方法,采用动态震源随机编码技术和波场分离技术,压制多震源串扰噪声和纵、横波耦合引起的串扰效应,实现波场分离.基于波动方程、散度和旋度的波场分离方法,目前在实际资料处理中较少应用,多用于理论模型研究试算.极化滤波方法,或严重依赖地表地层信息,或对振幅和相位的要求高,在应用上存在很大局限.F-K滤波、τ-p变换、Radon变换等滤波方法,会出现信号与噪声(其他分量信号、随机噪声、规则噪声等)在所处变换域内分布范围重叠的问题,从而造成滤波结果存在信号被去除或噪声无法彻底去除现象,并且还会因方法的局限性造成混波、假频等现象.
多波地震数据纵横波的速度差异明显,理论上纵、横波对自身速度的叠加响应最强、其他速度叠加响应为零,因此不同速度生成的叠加道可视为由该速度对应的地震信号叠加生成.横波速度动校正后的CCP道集内,各道同时刻的横波信号代表同一转换点信息,它们与同时刻的叠加道S变换谱存在相似关系(Pinnegar and Eaton,2003;赵淑红和朱光明,2007;王云专等,2010).基于多波地震数据的叠加速度响应特性和频谱特性,本文提出基于CCP道集S变换谱相似性的多波地震数据横波波场提取方法,它是一种基于数据频谱相似性分析的自适应全频带横波波场提取方法,该方法不会破坏横波信号的频谱和时空分布.理论和实际数据试算表明,本文方法能够有效提取多波数据中的横波波场.
1 方法原理
1.1 横波分量中的纵波投影及去除
多波多分量地震勘探因为测线观测方向(检波器接收方向)与各分量地震波的振动方向存在角度,从而产生观测角度旋转问题,造成接收的各分量信号中包含其他分量信号的投影,各分量信号也会因为自身信号投影到其他分量而产生振幅损失.在地表三分量观测系统中,纵波的振动方向与纵波接收方向相同,所以纵波分量不存在角度旋转问题;SV 分量和SH分量则因波的振动方向与接收方向存在角度而产生振幅损失,需做角度旋转使它们的振幅恢复到原始振幅.如图1所示,Y、Z轴分别代表角度旋转前的SV分量、SH分量,Y′、Z′轴分别代表角度转换后的SV分量和SH分量,ψ为接收方向与振动方向的夹角(可由地震数据道头中信息计算得出),两坐标系关系如下:
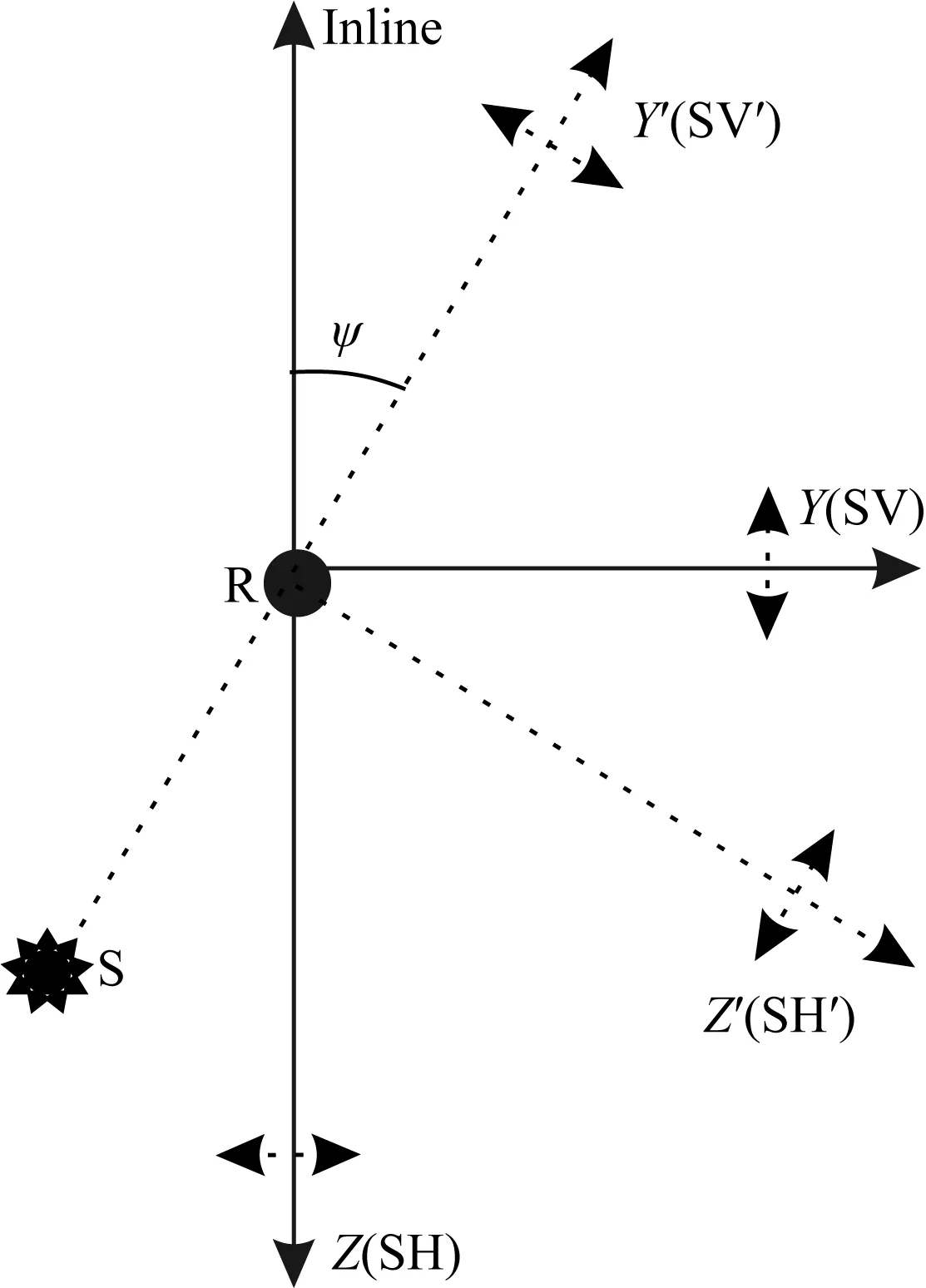
图1 三分量的观测系统角度旋转示意图Fig.1 The angle rotation diagram of three component geometry
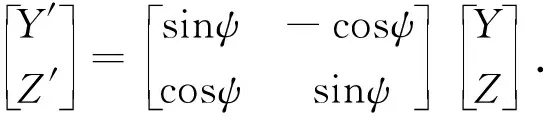
(1)
检波器会因人为摆放、自身误差等原因与测线方向产生一定的随机角度误差,造成各分量信号在其他分量产生投影(如图2),使各分量信号自身产生振幅损失.以图3所示纵波投影为例,X″、Y″、Z″轴分别代表随机角度误差旋转后的纵波、SV波和SH波分量,θx、θy和θz分别代表X″、Y″、Z″轴的随机误差角度,X′、Y′、Z′分别代表观测方位角度旋转后的纵波、SV波和SH波分量,两坐标系关系如下:
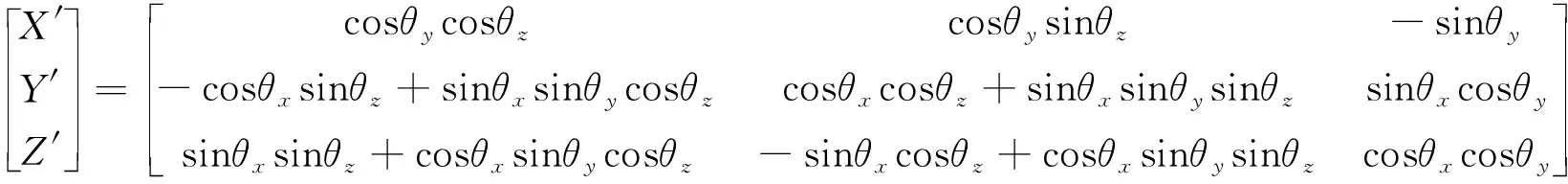
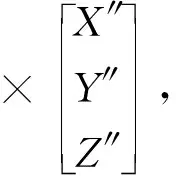
(2)
(3)
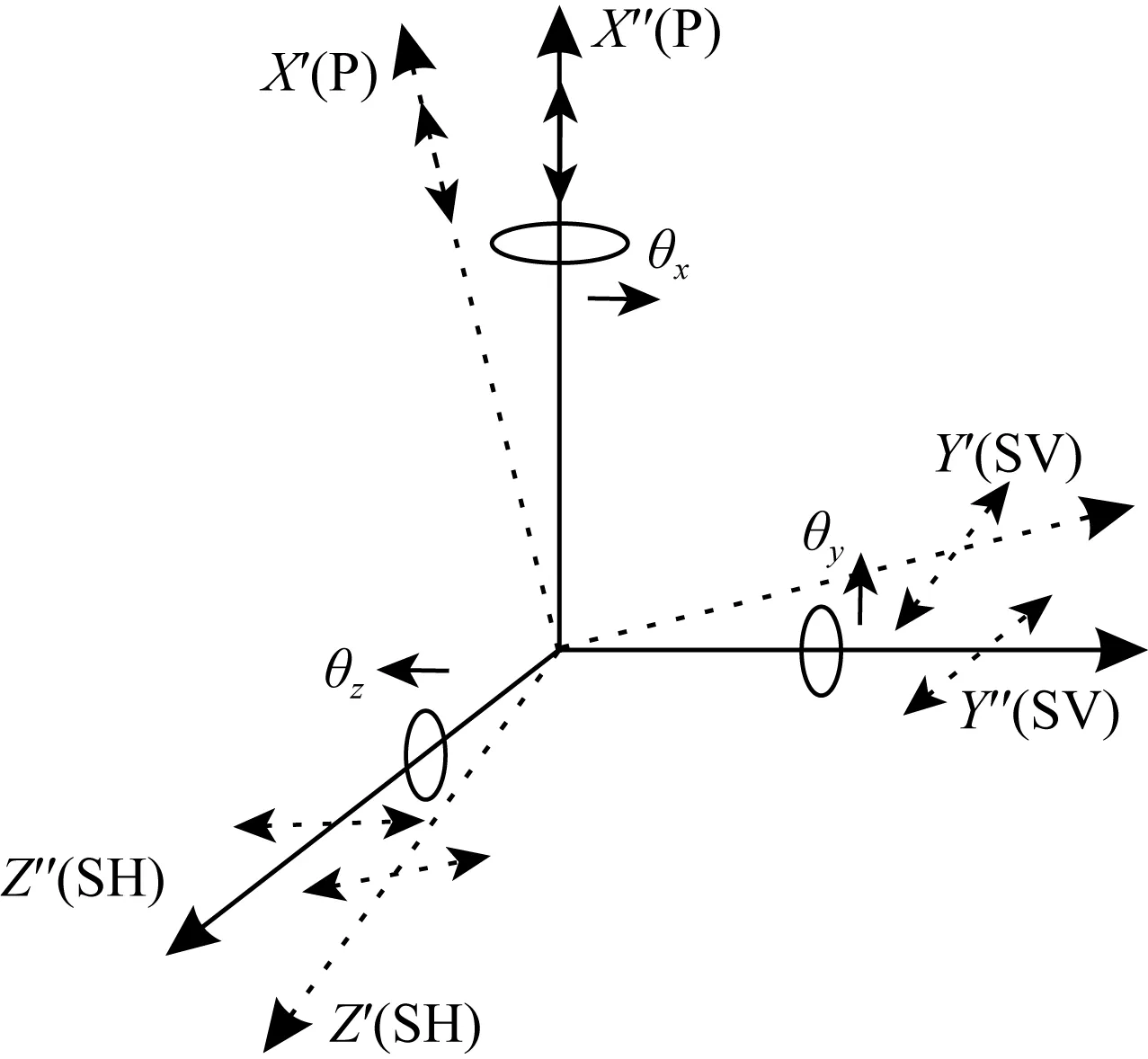
图2 三分量摆放角度旋转示意图X″、Y″、Z″轴分别代表随机误差角度旋转后的P、SV和SH波,X′、Y′、Z′分别代表观测方位角度旋转后的P、SV和SH分量,θx、θy和θz分别代表X″、Y″、Z″轴的随机误差旋转角度.Fig.2 The angle rotation diagram of three component layoutX″, Y″, Z″ axes represent P-, SV- and SH- waves respectively after random error angular rotation, X′, Y′, Z′ axes represent P-, SV- and SH- waves after the rotation of observation azimuth angle, θx, θy and θz represent the random error rotation angle of X″, Y″, Z″ axes.

图3 单波在各分量上投影示意图Fig.3 The schematic diagram of single wave projection on each component
多波地震数据的纵、横波间速度差异大,纵波在时间域内的振幅、频率等属性比较稳定.根据叠加统计效应,在CMP道集应用纵波速度叠加所得的叠加结果中,纵波信号的叠加响应最强,横波信号的叠加响应为0,因此可视纵波速度叠加所得叠加道为道集内纵波信号的叠加结果,如式(4):
(4)
式中,i为分量,i∈(X′、Y′、Z′);x、y、z分别为i分量中的纵波、SV波、SH波;k为道号,k=1,…,N,N为道集中的道数;Aix为i分量的纵波叠加信号;Aixk、Aiyk、Aizk分别为i分量中各地震道内的纵波、SV波、SH波信号;nik为i分量第k道中的随机噪声.
由式(4)可知,如果对观测角度旋转后的多波地震数据各分量CMP道集分别应用纵波速度动校正,并对CMP道集中地震道减去该道集的纵波叠加道,则各CMP道集内纵波叠加结果为0,相当于将纵波波场从多波数据中去除;CMP道集内各道的纵波信号存在振幅差异,使各道在减去纵波叠加道后会产生残余纵波,但残余纵波的叠加结果为0,与随机噪声的叠加结果相同,因此可将残余纵波视为随机噪声,而SV波和SH波信号不受损失.因此,式(3)可简化为式(5):
(5)
在随机角度误差较小情况下,式(5)中cosθy和cosθz趋于1、sinθy和sinθz趋于0,式(5)可进一步简化为式(6):
(6)
式(6)中可知,在随机角度误差较小情况下,做过角度旋转的多波地震数据在减去纵波波场后,所得各横波分量结果可近似为还原的横波分量波场.
综上,对角度旋转后的多波地震数据各横波分量CMP道集应用纵波速度动校正,并对CMP道集中各道减去其纵波叠加道,可以有效去除多波地震数据中的纵波波场,数据中的残余纵波呈随机噪声形态分布;并且在随机角度误差较小情况下,所得各横波分量结果可近似为还原的横波波场.
1.2 横波速度动校正的CCP道集S变换谱分析
S变换(Stockwell et al.,1996)是介于短时傅里叶变换和小波变换之间的非平稳信号分析方法,其与傅里叶谱直接相关且可逆.由佐普里兹(Zoeppritz)方程可知,相同时刻各道横波信号振幅是随偏移距变化的.横波分量地震数据的CCP道集应用横波速度动校正后,各道同时刻样点代表同一转换点,因此在不考虑各向异性的前提下,它们的S变换谱在频率分布和相位分布上相同,但振幅不同,它们的关系为相似关系.
根据傅里叶变换的线性性质和尺度变换性质、傅里叶变换与S变换的关系、叠加统计原理,多波地震数据的横波分量在做过角度旋转及纵波波场减去后,对其CCP道集应用横波速度动校正,其叠加道的S变换正变换可表示为:
(7)
式中T为时间采样间隔,k∈[0,N),j∈[0,N),N为时间采样点数;R为道数,r为道号;Sr为第r道的横波信号S变换;Snr为第r道的噪声S变换,Snr包含随机噪声和残余纵波两部分.
由式(7)可知,应用横波速度动校正的CCP道集叠加道,其S变换谱中残余纵波和随机噪声的叠加结果为0,是横波信号S变换谱的叠加结果;因为道集内各地震道同时刻的S变换谱存在相似性,所以同时刻的叠加道S变换谱与各地震道S变换谱也为相似关系.
综上,多波地震数据横波分量CCP道集应用横波速度动校正后,其叠加道由道集内横波信号叠加生成,叠加道的S变换谱为道集内各道横波信号S变换谱叠加而成,同时刻的叠加道S变换谱与各道横波信号S变换谱为相似关系.
1.3 滤波器设计及算法流程
实际多波地震数据因地层各向异性、转换点位置、旅行路径等原因,造成横波速度动校正后的横波分量CCP道集中各道同时刻横波信号产生振幅和相位差异,也使地震道中横波信号与同时刻叠加道信号的振幅和相位产生差异.因此在设计滤波器对横波速度动校正后CCP道集滤波时,在利用各道横波信号S变换谱与同时刻叠加道S变换谱的相似性提取地震道中横波信号的同时,还需要考虑同时刻各道横波信号的各向异性,在滤波结果中保留各向异性属性.
本文基于上述思路进行自适应滤波器设计.首先,将地震道振幅水平调整至叠加道振幅水平,使地震道S变换谱与叠加道S变换谱处于相同振幅水平,便于利用地震道S变换谱与同时刻叠加道S变换谱的相似性进行滤波.然后,根据同时刻地震道S变换谱中各频率成分与叠加道S变换谱中对应频率成分的各向异性程度,对地震道S变换谱进行自适应滤波,使得在提取地震道中横波信号的同时,在滤波结果中保留横波信号的各向异性属性.最后,将滤波结果的振幅水平调整至滤波前振幅水平,完成保幅处理.滤波器具体设计如下:
(1)振幅调整
对地震道和叠加道的主要反射层位分别开小窗口进行振幅统计,分别计算两道在各对应层位窗口的振幅比值系数,层位间的振幅比值系数由上下两层的振幅比值系数内插获得.将地震道各采样点振幅乘以振幅比值系数,使地震道振幅水平调整至叠加道振幅水平.具体如(8)式:
(8)
式中R为振幅比值系数,Ac为叠加道振幅,A为地震道振幅,A′为振幅调整后的地震道振幅,k为振幅统计窗口起始位置,m为振幅统计窗口结束位置,i、j为采样点,i∈(k,m),j∈(k,m).
(2)自适应滤波器
对叠加道和调整振幅后的地震道分别做S变换,参考非局部均值滤波方法(王胜春,2018)设计自适应滤波器.自适应滤波器包括三个主要参数:第一个参数是地震道S变换谱与同时刻叠加道S变换谱的各频率成分相对距离系数dijk,用于统计地震道S变换谱与叠加道S变换谱间各频率成分的振幅差异程度;第二个参数是根据相对距离系数dijk,计算对地震道S变换谱中各频率成分进行振幅调整的自适应加权系数Rijk,用来改善地震道S变换谱与叠加道S变换谱的相似性,去除地震道S变换谱中的残余纵波和噪声,提取横波信号;第三个参数是加权系数Rijk中的各向异性系数h,通过改变h值的大小调整加权系数Rijk对地震道S变换谱振幅的调整能力,确保滤波结果保留地震道中横波信号的各向异性属性.各参数具体如下:
(9)
(10)
式(9)中Sijk为地震道的S变换振幅值,Scjk为叠加道的S变换振幅值,i为道号,j为采样点,k为频率,N为采样点数.式(10)中的h≥1.各向异性系数h控制加权系数的收敛速度和滤波结果的各向异性程度,滤波结果与模型道的相对距离系数不超过h,各向异性系数h的取值视地震数据的各向异性情况而定.h取值越小,所得滤波结果的各向异性程度越小;h取值越大,所得滤波结果的各向异性程度越大.
滤波时,以叠加道S变换谱各频率的实部、虚部与其对应的振幅系数及自适应加权函数的乘积,作为地震道S变换谱各频率成分的各向异性属性,将所得各向异性属性与叠加道S变换谱中对应的实部、虚部相加,即得到滤波结果Sfijk.以此来提取地震道S变换谱中的横波成分,消除地震道S变换频谱中的残余纵波和噪声成分,保留地震道的各向异性属性.具体如下:
(11)
式(11)中的RS为实部振幅系数,RI为虚部振幅系数,具体如下:
(12)
对滤波得到的S变换谱反S变换,得到提取的横波信号.
(3)振幅恢复
因在滤波前需将地震道的振幅水平调整至叠加道振幅水平,故滤波结果的振幅水平与原地震道振幅水平不同,其振幅水平与叠加道振幅水平相同,故需将滤波结果的各采样点振幅除以式(8)中对应的振幅比值系数R,使滤波结果的振幅水平恢复至滤波前振幅水平.
本文方法的具体算法流程图如下(图4):
(1)输入做过预处理的多波地震数据,并做纵波速度分析;
(2)对输入的多波地震数据横波分量CMP道集做纵波速度动校正,并在道集中减去叠加道;
(3)对减去纵波波场的横波分量CMP道集做纵波速度反动校正,并在CCP道集做横波速度分析及横波速度动校正;
(4)对横波速度动校正后的横波分量CCP道集内地震道做振幅调整,并对地震道和叠加道做S变换;
(5)以叠加道S变换谱为参考对地震道S变换谱滤波,并对滤波结果做反S变换和振幅恢复;
(6)输出滤波结果,即在多波地震数据中提取的横波波场.
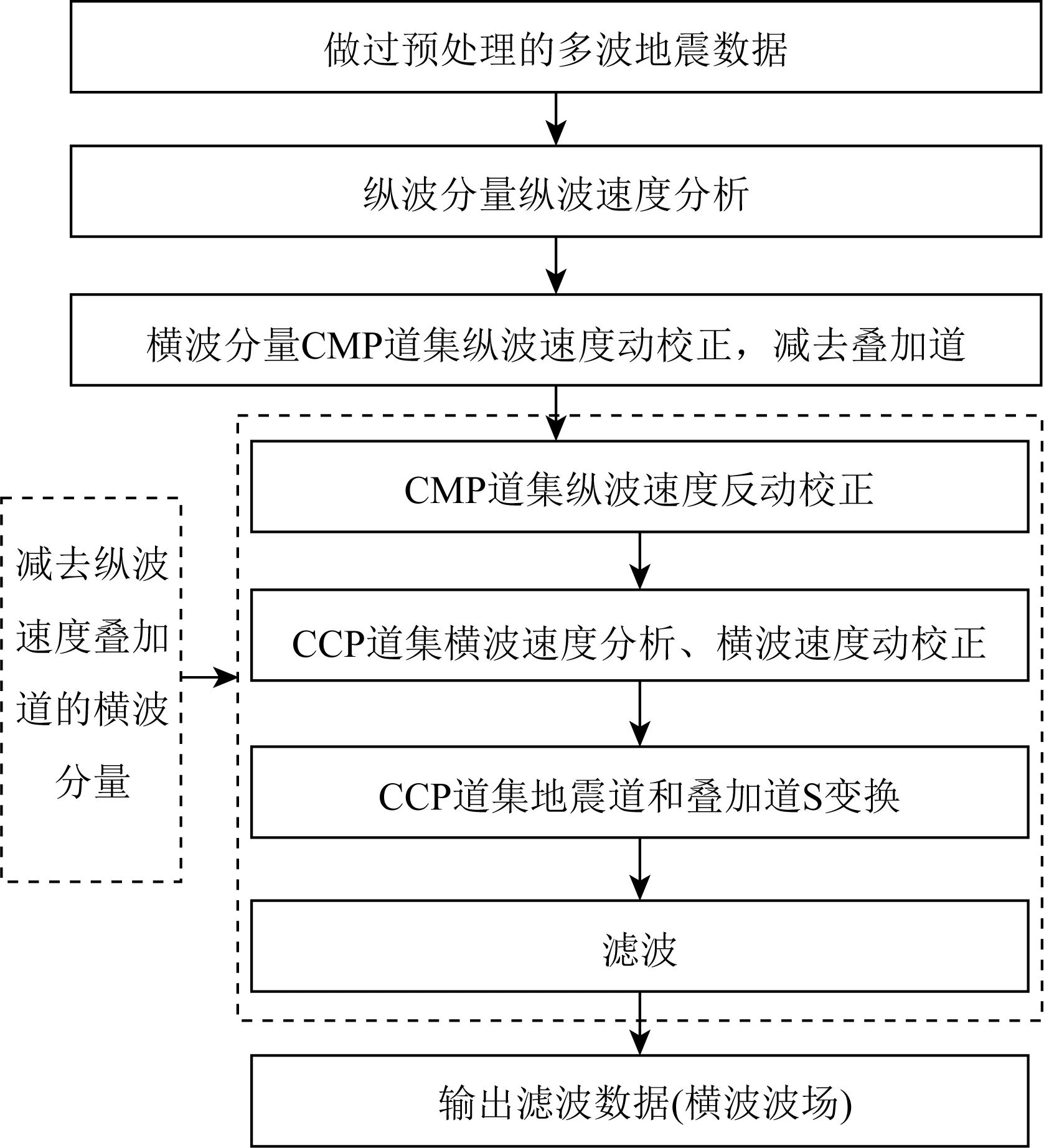
图4 算法流程图Fig.4 The algorithm flow chart
本文方法应用前需注意以下事项:
(1)滤波前需对多波地震数据做角度旋转、去噪、振幅补偿和初至切除等工作,以确保叠加道的信噪比和准确性.
(2)动校正所用速度场要精准.首先,本文方法通过在地震道中减去纵波叠加道来去除纵波波场,纵波波场去除的精度与纵波速度的精度直接相关;其次,本文方法以横波速度叠加道S变换谱为参考,对横波速度动校正后的地震道做S变换谱滤波,滤波结果与横波速度精度直接相关.
(3)考虑到异常振幅噪声和其他噪声对叠加道的影响,叠前最好对各道相同时刻采样点振幅排序,剔除最大值和最小值部分.本文取排序后振幅的中间三分之一部分振幅值进行叠加,以避开噪声对叠加道的影响,具体如式(13).
(13)
式中Am为叠加信号,Ami为振幅排序后的振幅序列,非原振幅序列,i为道号,m为采样点.
2 理论数据试算
本文使用弹性波有限差分正演模拟得到的P-SV多波地震数据进行试算.道集数据滤波过程及结果见图5.图5a为多波地震数据应用纵波速度动校正后的CMP道集,道集中1000 ms、1700 ms、2400 ms、2900 ms四组水平同相轴反射波组为纵波反射,呈双曲线形态分布的波组为转换横波;图5b为图5a数据中各地震道减去纵波叠加道后结果,四组纵波反射在图5b中得到很好去除,尤其2400 ms处的纵波波组在纵波波场减去前严重压制了与其相交的横波波组,减去纵波波场后,该组横波的信噪比和连续性得到明显改善.图5c为减去纵波波场后的横波分量CCP道集应用横波速度动校正后结果,图中可见明显的纵波残余,其能量主要集中在近道.图5d为图5c数据经本文方法滤波的结果,经本文方法滤波后,数据中的残余纵波得到去除,横波波场得到有效提取,各组横波反射的振幅特征得到了保留.
图6为滤波前后地震道及叠加道的S变换谱.图6a—d分别为图5c(滤波前)道集中第27、37、60、70道的S变换谱,图6f—i分别为图5d(滤波后)道集中第27、37、60、70道的S变换谱,图6e为叠加道的S变换谱.道集中有1450 ms、2300 ms、3250 ms、3950 ms四组SV波,图6的S变换谱中a、d、f和i所在地震道因为动校拉伸切除而缺少浅层1450 ms处SV波,因此它们的S变换谱也缺少该层的S变换谱.因滤波是以同时刻叠加道S变换谱为参考对地震道S变换谱进行滤波,所以在这些地震道的滤波过程中,该层S变换谱的缺失不影响其他层位的滤波.滤波前,图6a—d的S变换谱中均存有较强噪声,其中图6b和图6c的S变换谱中,3250 ms、3950 ms两组SV波的S变换谱基本淹没在噪声中;与叠加道S变换谱(图6e)对比,各道的SV波S变换谱在叠加道S变换谱中均有对应,并且地震道S变换谱中的噪声在叠加道S变换谱中得到有效去除.对比滤波前后各道的S变换谱,滤波后各道的SV波S变换谱得到有效提取,残余纵波和噪声得到有效分离.
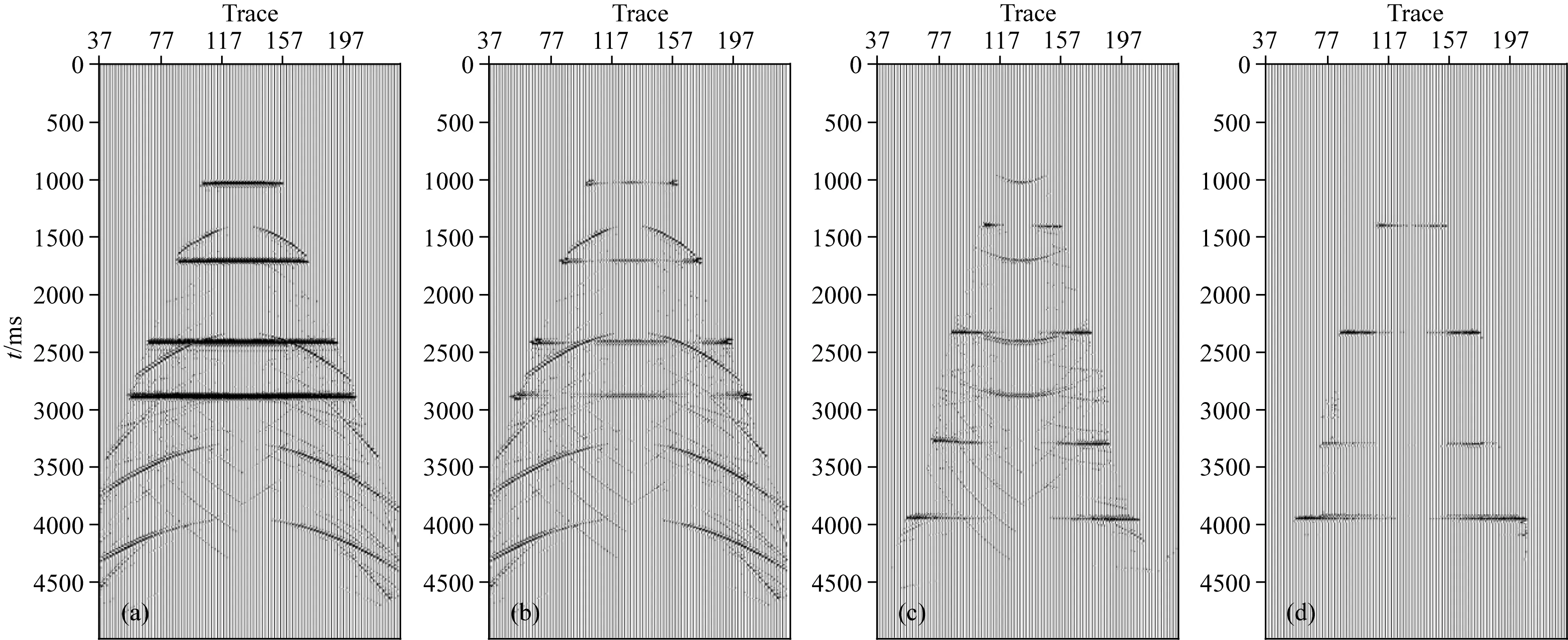
图5 多波数据道集提取横波波场示意图(a) P波速度动校正的CMP道集; (b)(a) 图数据减去叠加道后; (c) 减去P波后的横波速度动校正CCP道集; (d)(c) 图数据应用本文方法滤波结果.Fig.5 The schematic diagram of S-wave field extraction from multi-wave data gathers(a) CMP gathers after P-wave velocity NMO;(b) After subtracting stack trace from (a) data;(c) The CCP gathers of S-wave velocity NMO after P-wave subtraction;(d) The filtering results of (c) data by this method.
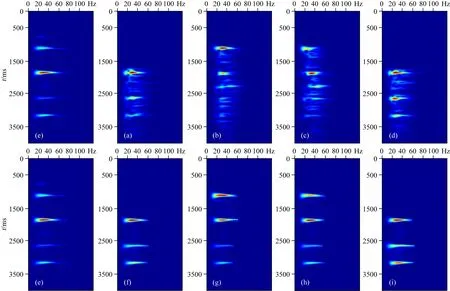
图6 滤波前后地震道及叠加道的S变换谱(a) 滤波前第27道; (b) 滤波前第37道; (c) 滤波前第60道; (d) 滤波前第70道; (e) 叠加道; (f) 滤波后第27道; (g) 滤波后第37道; (h) 滤波后第60道; (i) 滤波后第70道.Fig.6 S-transform spectrum of stack trace and seismic traces before and after filtering(a) The 27th trace before filtering; (b) The 37th trace before filtering; (c) The 60th trace before filtering; (d) The 70th trace before filtering; (e) The stack trace; (f) The 27th trace after filtering; (g) The 37th trace after filtering; (h) The 60th trace after filtering; (i) The 70th trace after filtering.
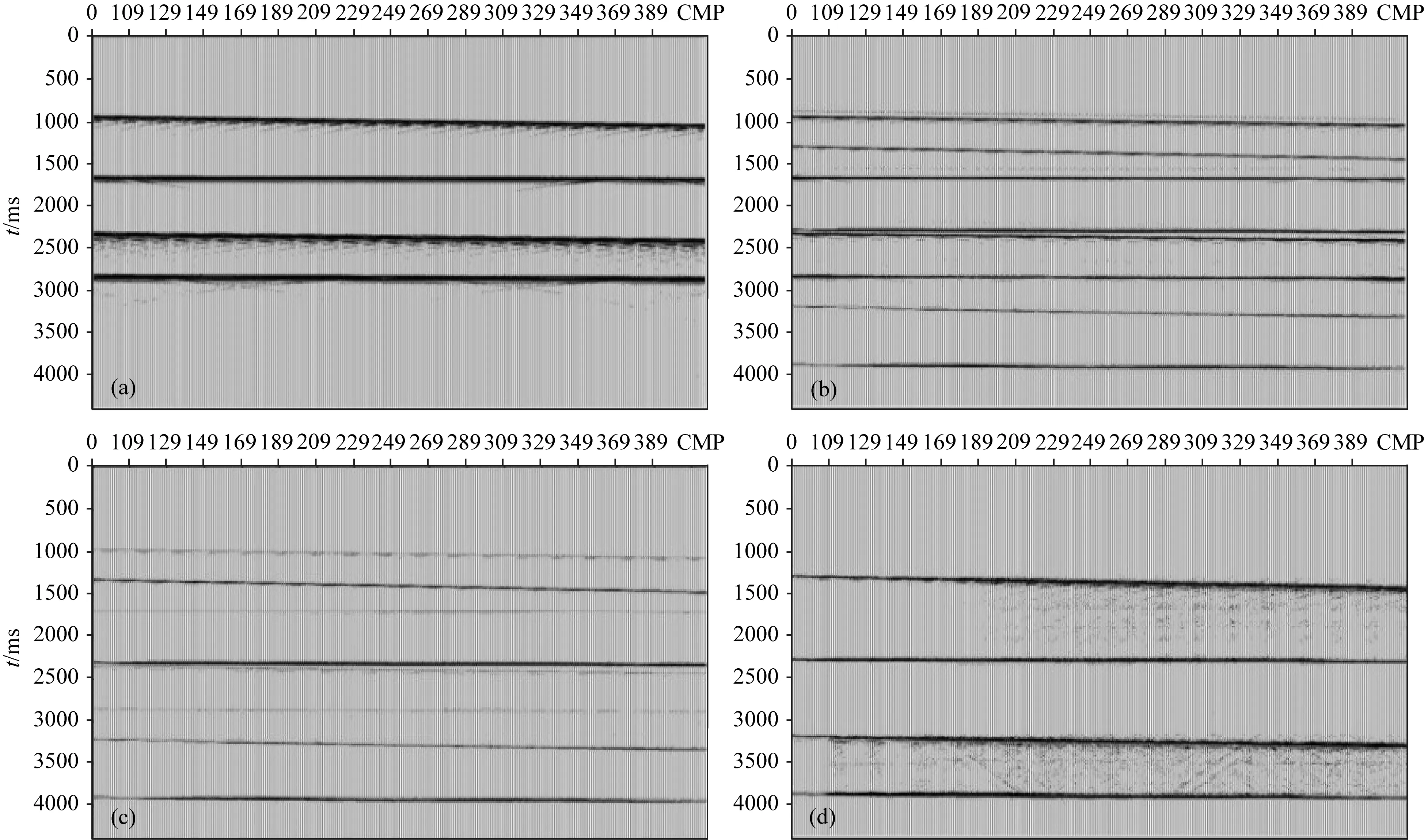
图7 横波波场提取叠加剖面图(a) 多波地震数据的纵波速度叠加剖面; (b) 多波地震数据的横波速度叠加剖面; (c) 减去纵波波场后的横波速度叠加剖面; (d) c剖面叠前数据应用本文滤波方法提取的SV波波场数据叠加剖面.Fig.7 The stack section map extracted from S-wave field(a) The stack section of multi-wave seismic data by P-wave velocity; (b) The stack section of multi-wave seismic data by S-wave velocity; (c) The stack section of wavefield subtracted P-wave field by S-wave velocity; (d) The stack section of SV-wave field data extracted from the pre-stack data of section c by this method.
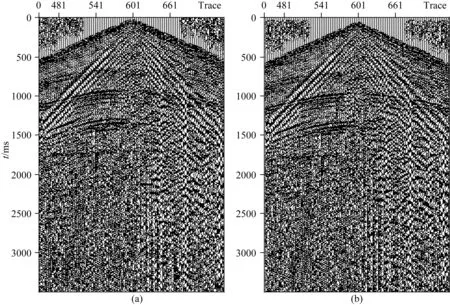
图8 SV分量角度旋转前(a)、后(b)对比Fig.8 The comparison diagram of SV component before (a) and after (b) angular rotation
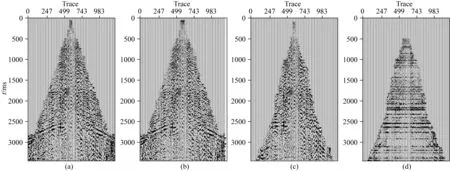
图9 SV分量提取SV波波场图(a) P波速度动校正的CMP道集; (b) a数据减去P波后的CMP道集; (c) 减去P波波场的SV分量地震数据应用横波速度动校正的CCP道集; (d) c数据滤波结果.Fig.9 The wavefield diagram of SV-wave extracted from SV component(a) The CMP gather after NMO by P-wave velocity; (b) The CMP gather subtracting P-wave from data a; (c) The CCP gather after NMO by S-wave velocity from SV component seismic data subtracting P-wave wavefield; (d) The filter result of data c.

图10 SV分量提取SV波波场叠加剖面(a) SV分量的纵波速度叠加剖面; (b) SV分量的横波速度叠加剖面; (c) 减去P波波场后的SV分量CCP道集应用横波速度动校正的叠加剖面; (d) c剖面叠前数据滤波提取的SV波波场数据叠加剖面.Fig.10 The stack section of SV-wave extracted from SV component(a) The stack section of SV-component by P-wave velocity; (b) The stack section of SV-component by S-wave velocity; (c) The stack section of CCP gather of SV component after subtracting P-wave field by S-wave velocity NMO;(d) The stack section of SV-wave field data extracted from the pre-stack data of section c.
图7为横波波场提取过程的各步叠加剖面.图7a为多波地震数据SV分量应用纵波速度叠加生成的剖面,剖面上的四组波组为纵波叠加生成,剖面上无SV波成像;图7b为SV分量应用横波速度叠加生成的剖面,剖面上有八组波组,与图7a波组对应的四组波组为纵波成像生成,另外四组为SV波叠加生成,图7b表明多波地震数据横波分量中的纵波投影对SV波成像有严重影响,尤其2400 ms处纵波波组与SV波波组严重交织而无法区分;图7c为纵波波场减去后的SV分量应用横波速度叠加生成剖面,剖面中的纵波波组虽然得到去除,但仍有残余纵波成像,依然对SV波成像产生影响;图7d剖面为图7c剖面的叠前数据应用本文方法提取SV波波场的叠加剖面,应用本文方法后,图7c剖面中的残余纵波成像在图7d中得到了完全去除.理论数据试算表明,本文方法可以有效提取多波地震数据中的横波波场.
3 实际数据试算
本文选取一条二维三分量多波地震数据进行试算,对该数据进行SV分量波场和SH分量波场的提取,以验证本文方法的横波波场提取能力.
图8为SV分量数据角度旋转前后对比.图8a为角度旋转前炮集记录,图8b为角度旋转后炮集记录.1000~1200 ms、1200~1600 ms两组SV波的相位、连续性和波组特征,在角度旋转后明显变好.
图9为SV分量道集数据滤波过程及结果.图9a为纵波速度动校正后的CMP道集,图9b为图9a数据减去纵波波场后数据;图9c为SV分量地震数据去除纵波波场后,应用横波速度动校正的CCP道集数据,图9d数据为图9c数据应用本文方法的滤波结果.
图10为SV波波场提取过程的各步叠加剖面.图10a为SV分量CMP道集地震数据应用纵波速度叠加所得剖面,图10b为SV分量CCP道集地震数据应用横波速度叠加所得剖面,图10c为减去纵波波场后的SV分量CCP道集应用横波速度叠加所得剖面,图10d剖面为图10c剖面的叠前数据应用本文方法所得数据叠加生成.
综合对比分析图9和图10可见,对SV分量CMP道集应用纵波速度叠加,所得叠加剖面(图10a)在1800 ms处存在一组高信噪比的残余纵波成像,在CMP动校道集的对应时间(图9a)也存在明显的纵波反射;减去纵波波场后,在纵波速度CMP动校道集中,纵波波场基本得到去除(图9b),在CCP道集应用横波速度叠加所得横波叠加剖面的信噪比得到有效提高,在纵波波场减去前(图10b)剖面上CCP8900~9200段2000 ms以上的信噪比极低,纵波波场减去后(图10c)的该段剖面信噪比得到显著提高;对纵波波场减去后的CCP道集地震数据应用本文方法滤波后,道集数据(图9d)和叠加剖面(图10d)的信噪比得到进一步提升.因此,本文方法可有效提取多波地震数据中的SV分量波场.
图11为SH分量道集数据滤波过程及结果.图11a为纵波速度动校正后的CMP道集,图11b为图11a数据减去纵波波场后数据;图11c为SH分量地震数据去除纵波波场后,应用横波速度动校正的CCP道集数据,图11d数据为图11c数据应用本文方法滤波后结果.
图12为SH波波场提取过程的各步叠加剖面.图12a为SH分量CMP道集地震数据应用纵波速度叠加所得剖面,图12b为SH分量CCP道集地震数据应用横波速度叠加所得剖面,图12c为减去纵波波场后的SH分量CCP道集应用横波速度叠加所得剖面,图12d剖面为图12c剖面的叠前数据应用本文方法所得数据叠加生成.
综合对比分析图11和图12可见,对SH分量CMP道集应用纵波速度叠加,所得叠加剖面(图12a)在1800~2700 ms处存在多组残余纵波成像,在CMP动校道集上对应时间的纵波反射不明显(图11a);减去纵波波场后,纵波速度CMP动校道集变化不明显(图11b),但在CCP道集应用横波速度叠加的剖面上信噪比得到明显改善,减去纵波波场后的叠加剖面(图12c)上1800~2700 ms处的信噪比,较减去前叠加剖面(图12b)有明显提高;对纵波波场减去后的CCP道集地震数据应用本文方法滤波后,道集数据(图11d)和叠加剖面(图12d)的信噪比得到进一步提升.因此,本文方法可有效提取多波地震数据中的SH分量波场.实际三分量多波数据试算结果表明,本文方法可以有效提取多波多分量地震数据中的横波波场.
4 结论
经理论多波地震数据和实际三分量多波地震数据试算验证,本文所提基于CCP道集S变换谱相似性的多波地震数据横波波场提取方法,可有效提取多波地震数据或多波多分量地震数据中的横波波场.
根据试算过程的数据分析和试算结果,对于多波多分量地震数据的纵横波波场分离,本文得出如下结论:
(1)多波多分量地震数据即使做过角度旋转,各横波分量信号中仍残存有相当比例的纵波信号投影,这些纵波投影会对横波信号的成像产生影响.
(2)对横波分量CMP道集地震数据应用纵波速度动校正,并在地震道中减去叠加道,可有效去除横波分量中的纵波投影,但数据中仍有以随机噪声形态分布的残余纵波,残余纵波的存在也会对横波信号的成像产生影响.
(3)横波速度动校正后的CCP道集内,地震道中的横波信号S变换谱与叠加道S变换谱存在相似性,利用这种相似性对减去纵波波场后的横波分量进行自适应滤波后,可有效提取多波地震数据中的横波波场、去除残余纵波.
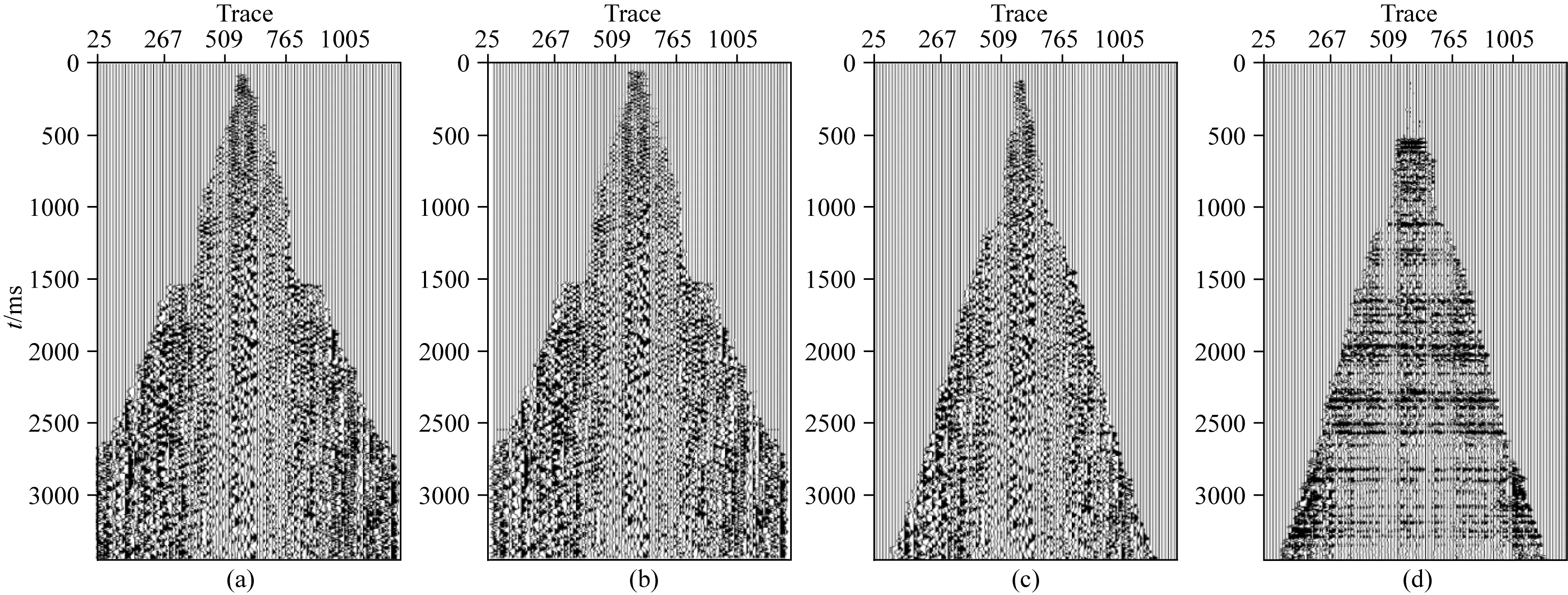
图11 SH分量提取SH波波场图(a) P波速度动校正的CMP道集; (b) a数据减去P波后的CMP道集; (c) 减去P波波场的SH分量地震数据应用横波速度动校正的CCP道集; (d) c数据滤波结果.Fig.11 The wavefield diagram of SH-wave extracted from SH component(a) The CMP gather after NMO by P-wave velocity; (b) The CMP gather subtracting P wave from data a; (c) The CCP gather after NMO by S-wave velocity from SH component seismic data subtracting P-wave wavefield; (d) The filter result of data c.

图12 SH分量提取SH波波场叠加剖面(a) SH分量的纵波速度叠加剖面; (b) SH分量的横波速度叠加剖面; (c) 减去P波波场后的SH分量CCP道集应用横波速度动校正的叠加剖面; (d) c剖面叠前数据滤波提取的SH波波场数据叠加剖面.Fig.12 The stack section of SH-wave extracted from SH component(a) The stack section of SH-component by P-wave velocity; (b) The stack section of SH-component by S-wave velocity; (c) The stack section of CCP gather of SH component after subtracting P-wave field by S-wave velocity NMO;(d) The stack section of SH-wave field data extracted from the pre-stack data of section c.

