循环爆炸作用下地下洞室的动态响应及损伤累积

曹安生，王光勇，顿志林，任连伟，孙晓旺

（1. 河南理工大学土木工程学院，河南 焦作 454003；2. 南京理工大学机械工程学院，江苏 南京 210094）

近年来，随着城市化进程加快，地面空间已不能满足城市发展的需求。由于地下工程具有使用空间大、资源消耗少等优点，越来越多的商场、轨道交通及储存室等被修建在地下。这些地下工程是国民重要的日常活动场所，战时又可成为防护工程，因此地下工程的安全防护在民用和军事方面都有重要的意义[1]。钻地武器自问世以来一直威胁着地下工程的安全，近年来钻地武器的发展更迅猛，可以在击中目标后发生多次爆炸[2]，这对修建地下工程提出了更大的挑战。掌握循环爆炸作用下地下洞室的动态响应及损伤累积特征是提升此类地下工程抗爆性能的重要前提。

隧道爆破开挖、炸弹恐怖袭击和建筑物的爆破拆除等都是由多次爆炸构成的循环爆炸行为。循环爆炸对地下工程结构的影响非常复杂，前次爆炸引起的结构动力响应和损伤会对后续爆炸产生影响[3]。国内外学者对多次爆炸作用下结构的动力响应和损伤展开了广泛研究：章毅等[4]将循环爆炸荷载转化为一系列的脉冲荷载，研究多次爆炸荷载作用下梁的抗爆性能，并发现梁的承载力随着爆炸次数的增加不断下降；张斐等[5]基于水下爆炸鼓胀试验原理对水下钢板开展了多次爆炸试验，得到钢板的挠度增量随着爆炸次数的增加逐渐减小的结论；Chu 等[6]通过试验研究了损伤累积效应对新浇筑混凝土抗压强度和耐久性的影响，并得出新浇筑混凝土的爆破振动安全标准；杨建华等[7]利用有限元分析软件研究不同地应力水平下毫秒延迟爆破开挖诱发围岩损伤的机理；闫长斌等[8]、颜峰等[9]通过现场试验研究了循环爆炸作用下岩体的损伤累积效应，结果表明声波在岩体中的传播速度随着爆破次数的增加而降低；潘城等[10]、李允忠等[11]利用LS-DYNA 完全重启动技术，研究了循环爆炸作用下岩石的损伤累积效应；顾金才等[12]、Chang 等[13]通过岩土工程抗爆结构模型研究了拱顶爆炸作用地下锚固洞室的破坏模式；王光勇等[14]通过数值模拟研究了双爆源爆炸作用下地下洞室的动态响应。可以看出，虽然对循环爆炸作用下结构的动力响应和损伤的研究已经较为深入，但是此类研究成果很少涉及循环爆炸对地下洞室的影响，有关爆炸对地下洞室影响的研究多集中于单次爆炸情况。而实际上，循环爆炸在地下工程中较为常见，因此有必要对循环爆炸作用下地下洞室的动态响应和损伤累积展开研究。本研究将在相似模型试验的基础上，利用有限元软件分析循环爆炸作用下地下洞室的动态响应和损伤累积，从而为新建地下工程的抗爆设计及地下工程的支护优化提供参考。

1 数值模型

1.1 有限元模型

数值计算模型源自于相似试验模型，王光勇等[15]记录了试验装置和相关数据，因此这里只作简单的概述。该模型模拟了埋深20 m、跨度4 m 的洞室遭遇拱顶爆炸的情形。按照Froude 比例法，确定密度、长度、应力相似比尺分别为Kρ= 0.67、Kl= 0.09、Kσ= 0.06，相似换算后得到模型的宽、高和厚度分别为2.4、2.3 和1.5 m，洞室的跨度为0.6 m，如图1 所示。洞室由间距、排距和长度分别为4、4 和24 cm的单排全长黏结式锚杆锚固。洞室围岩按Ⅲ类岩体性质考虑，由砂、水泥、水、速凝剂按15∶1∶1.6∶0.016 6 的比例配合。洞室模型由4 个可以前后移动的刚性侧限装置固定，为消除爆炸波在侧面的反射，在装置的迎爆面设置了含孔率为50%的铝制消波板。模型试验中，100 g TNT 炸药在洞室拱顶上方0.83 m 处发生爆炸，如图1(a)所示。为了提高计算效率，考虑试验模型的对称性，数值计算时将其简化为平面应变问题。根据试验模型的尺寸进行建模，计算模型的左右边界和下边界设置为无反射边界条件，围岩的网格尺寸为1 cm。数值计算中通过向直径为20 cm 的爆腔上加爆炸荷载模拟TNT 爆炸，如图1(b)所示。图中： σ1、 σ2和 σ3为测点的应力，D1、D2、D3和D4为测点的损伤因子，U1、U2和U3为测点围岩的位移。

图1 地下洞室模型 （单位：厘米）Fig. 1 Model diagram of the underground cavern (Unit: cm)

为了对比分析高水平单次爆炸和低水平循环爆炸对地下洞室的影响，需要保证高水平单次爆炸和低水平循环爆炸作用到爆腔的总荷载水平相同。因此，设计低水平循环爆炸荷载试验强度为高水平单次爆炸试验强度的1/10，但保持单次爆炸作用时间不变，在爆腔内表面循环10 次。图2(a)为100 g TNT爆炸高水平单次爆炸试验后爆腔内表面的荷载-时程曲线，荷载作用时间为100 μs。图2(b)为低水平循环爆炸试验的荷载时程曲线，td为单次荷载作用时间100 μs，t0为施加荷载的间隔时间400 μs，t0能够确保前一次爆炸作用下洞室围岩的动力响应和损伤已经稳定。

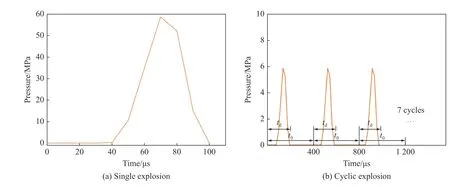
图2 爆炸荷载时程曲线Fig. 2 Explosion loading-time history curve

1.2 材料模型及参数

混凝土损伤塑性模型(Concrete damaged plasticity, CDP)能够反映岩石等脆性材料受到的拉力、压力损伤，常被用于爆炸作用下围岩的损伤模拟。Lee 等[16]对该模型进行了详细介绍，引入损伤因子D 描述围岩的损伤情况（0≤D≤1；0 表示无损伤，1 表示完全损伤；D 越趋近1，损伤越大）。CDP 模型的相关参数由试验测得，如表1 所示。其中：E、 μ、 σb0/σc0、Kc分别为材料的弹性模量、泊松比、双轴抗压强度与单轴受压极限强度之比、拉伸子午面与压缩子午面上的第二应力不变量之比。试验采用铝棒模拟锚杆，锚杆直径为1.84 mm，密度为3 000 kg/m3，弹性模量为76 GPa，泊松比为0.34。考虑铝棒的弹塑性 特性，在计算模型中采用理想的弹塑性模型模拟锚杆，屈服强度为282 MPa。

表1 CDP 模型相关参数Table 1 Parameters of the CDP model

2 结果与讨论

2.1 单次爆炸试验与模拟结果对比分析

图3 单次爆炸下测点的应力时程曲线对比Fig. 3 Comparison of the stress time curves of the measuring points of single explosion

为了验证模拟结果的准确性，将单次爆炸中试验[15]和模拟的应力时程曲线进行对比。取爆源正下方20、40 和60 cm 处为测点（图1（b）），对应的应力分别为 σ1、 σ2和 σ3，测量结果如图3 所示，其中正值为压应力，负值为拉应力。由图3 可知：应力时程曲线均为先迅速上升达到峰值，然后逐渐下降趋于稳定。数值模拟中3 个测点的压应力峰值略大于试验中相同测点的压应力峰值，但仍为同一个数量级。同时，20 cm 测点处试验测得的残余应力略大于模拟数据，而其他两个测点差别不明显。上述现象的产生与洞室围岩的地质条件有关。数值模拟中将围岩视为各向同性介质，而试验模型是水泥砂浆材质，在施工过程中围岩的密实是分层进行的，从而留下许多层面，能够增加应力波传播过程中消耗的能量。因此，试验中测点的压应力峰值小于模拟中同位置的测点。同样由于试验围岩中存在层面和空隙，围岩在爆炸后形成了不可恢复的残余变形，残余变形引发了残余应力，而数值计算中这种残余应力在各向同性的围岩中非常小。由于40 和60 cm 测点距离爆源较远，受到的爆炸力作用较小，所以产生的残余应力也较小。

《常规武器防护设计原理》[17]中用于描述应力波传播特性的应力波衰减公式为

式中： σmax为峰值压应力；R/W1/3为比例距离，R 为测点到爆源的距离，W 为装药量；c 为典型值，取决于炸药和材料的性质；n 为衰减因子，主要取决于材料的性能。

图4 为各测点的压应力峰值-比例距离拟合曲线。从图4 可知，试验和模拟的应力波衰减曲线相似，曲线开始较陡，随后变得平缓。说明比例距离较小时，围岩的压应力衰减速度比较慢，随着比例距离的增加，压应力的衰减速度逐渐减小。同时可以观察到，模拟中应力波的衰减指数为1.305，略小于试验中的衰减指数1.328，说明试验中应力波的衰减速度比模拟中的大，与图3 中的现象相符合。因此，数值模拟结果具有较高的可信度。

图4 压应力峰值-比例距离拟合曲线Fig. 4 Fitting curves of the peak pressure and the scaled distance

2.2 地下洞室的动态响应分析

2.2.1 应力波的传播规律

图5 循环爆炸模型中测点的应力-时程曲线Fig. 5 Stress-time curves of the measuring points of cyclic explosion

图6 压应力峰值-爆心距拟合曲线Fig. 6 Fitting curves of the peak pressure and the distance from the explosion source

为了分析循环爆炸中应力波的传播规律，图5给出了循环爆炸模型中20、40 和60 cm 测点的应力时程曲线，3 条曲线的压应力峰值随着测点距爆源距离的增加逐渐降低。对比图3 中单次爆炸的应力时程曲线可知，循环爆炸的应力时程曲线由单波峰变成了“十波峰”，由左到右依次爆炸。同时可以发现，低水平循环爆炸产生的压应力峰值远小于高水平单次爆炸，且循环爆炸的压应力峰值随着爆炸次数的增加整体呈减小趋势。为了研究循环爆炸对应力波衰减规律的影响，图6给出了各次爆炸中距爆源20、40 和60 cm 测点的压应力峰值 σmax与爆心距R 之间的幂函数拟合曲线。观察循环爆炸拟合曲线的衰减指数可以发现：前3 次的衰减指数逐渐减小，由0.968 降低到0.723，后7 次的衰减指数逐渐增大，由0.964 增加到2.027。衰减指数先减小后增大说明应力波的衰减速度先减小后增大。分析产生这种现象的原因是前3 次爆炸加密围岩中原有的空隙使裂隙减少变窄，应力波在传播过程中耗散的能量减少，致使第2、3 次爆炸时应力波的衰减速度减小，而后几次爆炸中由于围岩的损伤累积和围岩中裂缝增多，应力波传播过程中 消耗的能量逐渐增加，致使应力波的衰减速度越来越快。

2.2.2 洞室拱的位移分析

洞室拱距离爆源较近，分析洞室拱的位移对于研究洞室的破坏情况具有指导意义。为了对比分析高水平单次爆炸和低水平循环爆炸对洞室围岩位移的影响，分别在具有代表性的拱顶、拱腰和拱角处布置3 个测点，测量围岩的位移分别为U1、U2和U3，如图1(b)所示。单次爆炸和循环爆炸下3 个测点的位移时程曲线如图7 所示。由图7 可知，单次爆炸的位移时程曲线为先上升达到峰值，而后经历一段下降后趋于平稳。这是因为岩体变形包括弹性变形和塑性变形，当位移达到峰值后，弹性变形逐渐恢复，但塑性变形不可恢复。循环爆炸中，位移时程曲线是分阶梯上升的，即每次爆炸后洞室围岩的位移都会有一定程度的上升。同时还发现单次爆炸围岩的最终位移大于循环爆炸围岩的最终位移，分析原因：低水平爆炸作用下围岩产生的变形较小，可恢复的弹性变形比例较大，多次爆炸产生的位移累积也相对较小；高水平单次爆炸时围岩产生的变形较大，不可恢复的塑性变形所占比例较大，所以围岩最终位移较大。

图7 U1～U3 测点的位移时程曲线Fig. 7 Displacement-time curves of U1-U3

2.2.3 洞壁环向应变分析

洞壁的环向应变能够反映环向应力的大小。分别在洞室的拱顶、拱腰、拱角、直墙侧和直墙脚处布置应变测点，同时在相邻两测点的中间位置再布置一个测点，从拱顶到直墙脚测点的应变依次为ε1～ ε10，如图8 所示。图9 和图10 分别为单次爆炸和循环爆炸后洞壁测点的环向应变峰值，正值为拉应变，负值为压应变。

图8 应变测点布置Fig. 8 Arrangement of strain measuring points

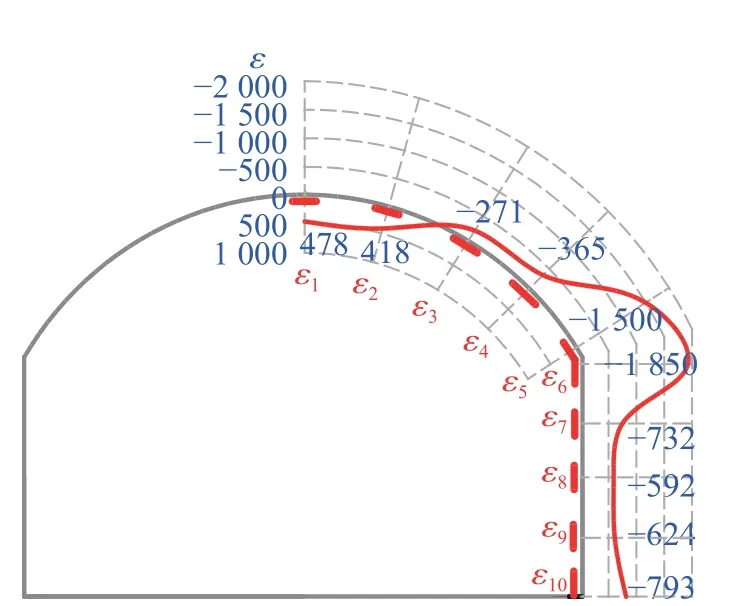
图9 单次爆炸时洞壁的环向应变峰值(单位：10-6)Fig. 9 Peak circumferential strain distribution of the cavern wall under single explosion (Unit: 10-6)

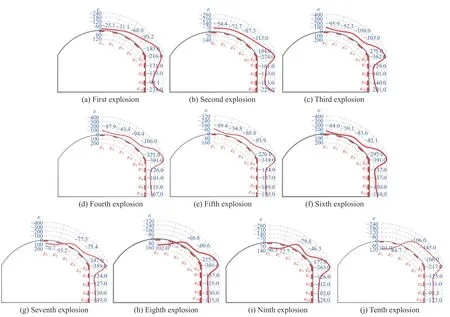
图10 循环爆炸时洞壁的环向应变峰值（单位：10-6）Fig. 10 Peak circumferential strain distribution of the cavern wall under cyclic explosion (Unit: 10-6)

由图9 可知，高水平单次爆炸下洞室拱顶部位的环向峰值应变为拉应变，拱腰附近处拉应变逐渐减小转为压应变，拱腰向下至直墙脚均为压应变。这是因为爆炸产生的压应力波传播到洞室自由面时发生反射形成拉应力，拉应力导致围岩发生拉应变。由图10 可知，低水平循环爆炸中洞室拱顶在前6 次爆炸中呈现压应变，至第7 次爆炸后呈现拉应变。前几次爆炸后围岩的强度还很高，虽然也有拉应变产生，但是很小；随着爆炸次数增多，围岩的破坏程度增大，围岩强度降低，从而拉应变不断增加。图9和图10 显示，洞室的环向应变由拱顶处至拱角处呈现先减小后增大的趋势，由拱角至直墙脚也是先减小再增大。这主要是因为拱角和直墙脚位于拐角处，易产生应力集中，所以应变较大。虽然拱顶的应变较小，但此处易产生拉应变，而围岩的抗拉能力远低于抗压能力，为此应在此处加强支护。

2.3 地下洞室的损伤累积分析

2.3.1 循环爆炸作用下地下洞室的损伤演化

为了研究洞室的损伤演化过程，选取循环爆炸过程中洞室损伤变化较明显的第1、2、3、6、8 和10 次爆炸进行分析。由于受压损伤对洞室的影响较小，所以只对受拉损伤进行分析。图11 为各次爆炸后洞室围岩受拉损伤分布。

由图11(a)可知，第1 次爆炸后，洞室围岩的损伤主要分布在爆腔周围、洞室拱和地表附近。爆腔附近的损伤呈圆形分布，并且随着与爆源距离增加，颜色由红色逐渐转为蓝色，说明围岩的损伤程度越来越小；地表附近的损伤呈条形分布，且中部厚度较大，越靠近两端越小；洞室拱附近的损伤呈拱状分布，且拱顶处围岩的损伤因子达到了0.9 以上，损伤较为严重，另外在锚固和未锚固区的交界处损伤也较为严重。如图11（b）所示，随着第2 次爆炸的发生，爆腔周围的损伤程度和范围都进一步增加，地表附近的损伤条中部向爆源方向扩展。洞室拱附近的损伤区向拱角方向延伸，直墙侧也产生了轻微损伤，锚固区和未锚固区交界处的损伤也沿其交界线延伸。图11（c）描述的第3 次爆炸后，爆腔周围增加了数条放射状损伤带，地表附近损伤条中部厚度进一步增加，洞室拱顶附近损伤区变化不明显，洞室底板中部出现了竖向损伤条。从图11(d)～图11(f)可以发现，随着爆炸次数的增加，地表中部向下扩展的损伤区和爆腔周围向上扩展的损伤区已经贯通，洞室拱顶和爆源间也形成了贯通的损伤带，锚固区和未锚固区交界处两侧的水平损伤区域已经到达模型的边界。洞室拱顶和直墙侧的损伤区在分布范围上并无明显变化，只是损伤程度略有增加。

图11 循环爆炸作用下洞室的损伤分布Fig. 11 Damage distribution of underground cavern under cyclic explosion

图12 单次爆炸洞室的损伤分布Fig. 12 Damage distribution of the underground cavern under single explosion

图12 为高水平单次爆炸作用后洞室围岩的损伤分布，与图11(f)对比可知：单次爆炸中爆腔周围和地表附近的损伤明显比循环爆炸的分布范围小，且在两者之间未形成贯通损伤。循环爆炸中爆腔周围放射状损伤带条数明显多于单次爆炸。两种爆炸洞室拱附近的损伤情况存在明显的不同，循环爆炸中拱顶的损伤区范围更大，单次爆炸中锚固区和未锚固区交界处拱形损伤区域厚度更大，但其两侧未延伸到模型的边界。在洞室底板处两者也存在明显不同，单次爆炸中损伤带更多且对称分布。总的来看，在总爆炸荷载水平相同的情况下，低水平循环爆炸对洞室围岩造成的损伤范围和程度明显大于高水平单次爆炸。

洞室最大受拉累积损伤面积可以反映循环爆炸作用下洞室的损伤累积过程。最大受拉损伤是指损伤指数达到0.98 以上的损伤。图13 为两种爆炸情况中洞室的最大受拉累积损伤面积。随着爆炸次数的增加，循环爆炸作用下洞室的最大受拉累积损伤面积不断增大。第10 次循环爆炸结束后洞室围岩的最大受拉累积损伤面积是第1 次爆炸的8.75 倍，是第2 次爆炸的5.25 倍，是第5 次爆炸的2.17 倍。另外，第8 次爆炸时引起的洞室最大受拉累积损伤面积已经超过了高水平单次爆炸，当循环爆炸结束后，与单次爆炸相比，最大受拉累积损伤面积增加了28%。

2.3.2 循环爆炸作用下地下洞室的损伤累积规律

为了分析洞室围岩的损伤累积规律，分别测得爆源正下方 20、40、60 和80 cm 处4 个测点的损伤因子D1、D2、D3和D4，如图1（b）所示。图14 和图15 分别为单次爆炸和循环爆炸作用下各测点的损伤因子时程曲线。可以看出，爆炸作用下围岩损伤呈现不可逆增大趋势，而循环爆炸中各测点的损伤是分级增加的，且随着围岩累积损伤值的增加，围岩的损伤增量越来越小，表明后续爆炸对已经产生损伤的围岩进一步破坏，但围岩损伤累积的难度随着围岩损伤值的增加而越来越高。对比两种爆炸最终损伤情况可以发现：两种爆炸在20 和80 cm 测点处都达到了最大受拉损伤值，但是循环爆炸中40 和60 cm测点的损伤情况大于单次爆炸，增幅分别为22.4%和25.3%。可以看出，在总爆炸荷载水平相同的条件下，低水平循环爆炸对围岩造成的损伤情况大于高水平单次爆炸。

图13 洞室最大受拉累积损伤面积Fig. 13 The maximum tensile cumulative damage area of the underground cavern

图14 单次爆炸下各测点的损伤时程曲线Fig. 14 Damage time curves of the measuring points under single explosion

为了进一步研究洞室围岩的损伤累积与爆炸次数之间的关系，图16 中对循环爆炸中20、40、60 和80 cm 测点的损伤累积和爆炸次数进行拟合分析，N 为爆炸次数，4 条曲线的方差都大于0.97。从拟合方程中可以看出，围岩的损伤累积和爆炸次数呈显著的非线性关系。

图15 循环爆炸下各测点的损伤时程曲线Fig. 15 Damage time curves of the measuring points under cyclic explosion

图16 洞室围岩的损伤累积和爆炸次数拟合曲线Fig. 16 Fitting curves of the cumulative damage of the surrounding rock and explosion times

3 结 论

（1）循环爆炸中洞室围岩的应力波衰减速度随着爆炸次数的增加先减小后增大。

（2）爆炸荷载总水平相同时，高水平单次爆炸下洞室围岩的位移大于低水平循环爆炸，且循环爆炸中洞室围岩的位移是分级上升的。

（3）高水平单次爆炸作用下，拱顶处围岩产生了拉应变。低水平循环爆炸作用下，拱顶处围岩先产生压应变，随后随着爆炸次数的增加转变为拉应变。两种情况下，从拱腰向下到直墙脚，洞壁的环向应变均为压应变。由于应力集中，洞室的拱角和直墙脚处的应变较大，此处应加强支护。

（4）爆炸荷载总水平相同时，低水平循环爆炸对围岩产生的损伤在面积和程度上均大于高水平单次爆炸。洞室围岩的损伤在循环爆炸作用下呈不可逆的逐级增加，且累积损伤和爆炸次数之间呈明显的非线性关系。