螺旋拉胀纱线动态拉伸行为的数值模拟

戴金滔，王文强

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

泊松比是材料的基本力学特性参数之一，大多数材料的泊松比为正值。也有一些天然和人工设计的特殊材料的泊松比为负值，这类材料被统称为负泊松比材料，或者被形象地称为拉胀材料（意指纵向拉伸横向膨胀）。拉胀材料和结构由于具有奇特的拉胀特性以及由此带来的其他优异性能，近30 年来获得了广泛的关注[1-4]，在爆炸与冲击防护中也有重要的应用价值[5-11]。

螺旋拉胀复合纱线是一种典型的拉胀材料，由高模量纱线螺旋式缠绕低模量纱线组成。在准静态轴向拉伸作用下，原本蜷曲的包缠纱被逐渐拉直，直线的芯纱受到挤压变形为螺旋状，整体结构沿横向膨胀。

自2003 年Hook[12]发明螺旋拉胀纱线以来，国内外已开展的研究主要针对准静态载荷下如何优化材料和几何参数以充分增强纱线的拉胀效果[13-18]，动态响应方面的研究极少。英国一家公司开展了螺旋拉胀纱线织物的枪击和爆炸实验研究[19-20]，证明了其具有优异的抗弹抗爆性能；Zhang 等[21]用落锤实验研究了单根螺旋拉胀纱线在纵向冲击拉伸下的最大受力和能量吸收。总的来看，对螺旋拉胀纱线动态响应特性的认识还很粗浅。

为揭示螺旋拉胀纱线的抗冲击机理，本研究基于有限元模拟，首次开展螺旋拉胀纱线在纵向冲击作用下的应力波传播特性和动力学行为研究。

1 计算模型和准静态拉伸模拟结果

采用商业有限元软件ABAQUS 构建螺旋拉胀纱线的计算模型，并开展数值模拟研究。

计算模型由两个部件构成，可在ABAQUS CAE 中直接构建并装配。一个是直径较小的圆形截面的螺旋线，代表模量较高的包缠纱；另一个是直径较大的圆柱体，代表模量较低的芯纱。

考虑到模拟过程中芯纱和包缠纱剧烈变形，采用扫掠划分技术和中性轴算法，将芯纱划分为沙漏控制的减缩积分八节点线性六面体单元（C3D8R），采用自由网格划分技术，将包缠纱划分为十节点修正二次四面体单元（C3D10M）。在处理接触时，选择包缠纱为主面，芯纱为从面，法线方向为硬接触且不允许接触分离，切线方向为无摩擦或选用罚函数摩擦公式。由于网格划分采用了线性减缩积分单元，在每个方向上都比完全积分单元少一个积分点，从而产生沙漏问题，因此可根据网格变形伪应变能占系统总内能的比例评估计算是否失真。

考虑到芯纱和包缠纱的剧烈变形，本研究约定芯纱的初始轴线方向为复合纱线的纵向，与之垂直的方向为横向。为模拟复合纱线的纵向冲击拉伸行为，可固定纱线的一端，而赋予另一端恒定的纵向运动速度（以下简称加载速度）。在所有算例中，复合纱线都有足够的长度，以保证从加载端发出的单向传播的应力波特征充分发展，同时避免波在固定端反射干扰。

表1 列出了基本计算模型的材料及几何参数。其中，包缠纱和芯纱均为线弹性材料，其杨氏模量E 和泊松比 μ取自文献[17-18]，大致对应碳纤维和尼龙的参数。计算时还需设定的加载速度和摩擦系数随算例的不同而有所不同，将在后面说明。

表1 计算模型的材料和几何参数Table 1 Material and geometry parameters of the computational model

在进行动态拉伸模拟之前，先进行了准静态拉伸模拟（不计摩擦），以确保模型可以正确地呈现拉胀效应。结果表明，在纵向拉伸下，模型整体均匀伸长，包缠纱逐渐伸直并沿横向向内收缩，挤压芯纱迫使其变形为螺旋状并沿横向向外挤出。当整体拉伸度达到约6%时，复合纱线横向轮廓的宽度开始超过其初始宽度，呈现出拉胀效应。拉胀效应在拉伸度为6%～35%范围内都存在，并且10%左右时最显著。图1 显示了初始构型以及拉伸度达到10.5%和35.0%时的构型。

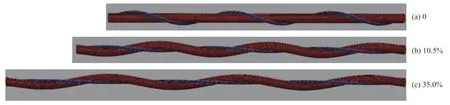
图1 准静态模拟呈现的拉胀效应：模型在拉伸度为0、10.5%、35.0%时的构型Fig. 1 Auxetic effect revealed from the quasistatic simulation: configurations of the model at elongations of 0, 10.5% and 35.0%

2 动态拉伸模拟结果和分析

2.1 双波与周期性横向膨胀现象

螺旋拉胀纱线由螺旋包缠纱和直线芯纱组成，如不考虑包缠纱和芯纱的相互作用，则在纵向冲击拉伸作用下，复合纱线中会出现彼此毫不相关的两个应力波：在包缠纱中沿纵向传播的一个应力波和在芯纱中沿纵向传播的另外一个应力波。

包缠纱中的应力波可参考螺旋弹簧中的应力波研究。这是一个相当复杂的问题，只有在一些特定的条件下才可以得到近似解。根据文献[22]，螺旋弹簧中的应力波同时伴随着纵向、扭转和剪切运动，其沿纵向的传播速度s 可按下式估算

式中： ρ为密度，c 为弹簧半径与弹簧丝半径之比（显然大于1）， θ为包缠角。

直线芯纱中的应力波相对简单，可近似为一维应力杆中的波，其波速由杨氏模量和密度决定，即

将表1 中包缠纱的参数代入式（1），芯纱的参数代入式（2），可计算出螺旋包缠纱和直线芯纱中传播的“纵波”波速分别为1 153 和1 033 m/s。可见，在不考虑包缠纱和芯纱的相互影响时，复合纱线中会并行地、毫不相干地在包缠纱中传播一个快波，在芯纱中传播一个慢波。

然而，实际上，由于包缠纱与芯纱之间存在着强烈的相互作用，任何一方的应力波在激发自身运动和变形的同时，也必然激发另外一方的运动和变形，并受到对方的反制，因此任何一方的应力波都不能脱离对方独立地传播。对于包缠纱而言，芯纱的存在使其波速不能按空心螺旋弹簧的波速（式（1））计算；对于芯纱而言，包缠纱的挤压使其变形为螺旋状，因此其波速也不能按一维应力杆的波速（式（2））计算。

为简化这个十分复杂的问题，不妨仍然假定在复合纱线中存在着分别由包缠纱和芯纱主导的一快一 慢两个波，引入等效模量 E*，将波速表示成如下普遍形式

显然，复合纱线中快慢双波的波速分别由包缠纱和芯纱的等效模量确定，且该等效模量考虑了对方影响。

对比式（1）、式（2）和式（3），可以看出，螺旋弹簧的等效模量为

对于一维应力杆，其等效模量 E*=E ；在材料相同的情况下，螺旋弹簧的等效模量 E*显然小于E。

复合纱线中包缠纱和芯纱的等效模量问题过于复杂，基本不可能得到解析表达式，但不妨进行定性的讨论。在复合纱线中，快波波阵面前方的区域为未受扰动的初始构型，由于包缠纱呈螺旋状，决定快波波速的包缠纱的等效模量必小于一维应力杆的等效模量，但直线芯纱的存在制约了螺旋包缠纱的自由运动和变形，因此包缠纱的等效模量又必大于空心螺旋弹簧的等效模量。同理，原本直线的芯纱在包缠纱主导的快波作用下预先变形为螺旋状，决定慢波波速的芯纱的等效模量必小于一维应力杆的等效模量，但包缠纱的存在制约了芯纱的自由运动和变形，因此芯纱的等效模量又必大于空心螺旋弹簧的等效模量。

于是可以推论，虽然不能用式（1）和式（2）分别计算包缠纱主导的快波和芯纱主导的慢波的波速，但是可以用式（1）确定快波和慢波波速的下限，用式（2）确定快波和慢波波速的上限。将表1 中包缠纱的参数代入式（1）和式（2），可估算出快波波速区间为1 153～9 000 m/s。将表1 中芯纱的参数代入式（1）和式（2），可估算出慢波波速区间为320～1 033 m/s。

模拟结果验证了上述分析，即在螺旋拉胀纱线中不存在只在某一根纱线中传播而不影响另一根纱线并反受其影响的应力波，但的确存在分别由包缠纱和芯纱所主导的一快一慢两个“纵波”，且其波速均处于上述估算的范围以内（详见2.2 节）。

图2 给出了0.1 ms 时某典型算例的对数应变云图（加载速度200 m/s，无摩擦），为达到最佳显示效果，特意将模型旋转，使之与屏幕（纸面）成一定角度。从ABAQUS 显示的应变云图动画，可以更清楚地看到动态变形和应力波传播的全过程。该过程可以描述如下：从加载端出发的由包缠纱主导的快波，在拉伸螺旋包缠纱的同时，也迫使直线芯纱变形为螺旋状。当快波传播一定时间，与一同出发的由芯纱主导的慢波拉开足够距离后，在快慢双波波阵面之间，出现了一种十分有趣的沿纵向周期性分布、随时间周期性变化的运动和变形现象。从动画可以直观地看到，快波波阵面拖曳着一串沿横向向外膨出的“鼓包”向前传播，每个“鼓包”大约由4 个芯纱螺旋环组成，每两个“鼓包”之间又间隔着另外3 个芯纱螺旋环。这种奇特的周期性现象只存在于快慢双波波阵面之间，在能量更高的慢波波阵面后方即消失，因此，慢波波阵面是一道分水岭。在视觉上，这种现象就如同从运动着的慢波波阵面等时间间隔地向前发射一个又一个脉冲。在图2 中，加载端位于模型的左端，A 区为快慢双波波阵面之间的区域，B 区为慢波波阵面后方区域，可以看到，在0.1 ms时A 区已经有4 个“鼓包”（图2 中De-max为“鼓包”最突出处的直径）。显然，如果时间和模型都更长，则快慢双波波阵面之间将制造出更多的“鼓包”。

图2 0.1 ms 时某典型算例的对数应变云图Fig. 2 Logarithmic strain contour of a typical simulation at 0.1 ms

为说明复合纱线中快波波阵面后方的每一处都经历了随时间的周期性变化，以图2 中芯纱的节点P 为代表，在图3 中画出了该节点的Mises 应力随时间的变化曲线。可以看到：快波到达后，应力呈现剧烈起伏的周期性变化；慢波到达后，应力显著提升。在慢波到达之前，压力曲线上有4 个完整的波峰和3 个完整的波谷，正好反映了图2中4 个完整的“鼓包”和3 个完整的“鼓包间间隔”经过节点P 的历史。压力曲线上的第4 个波谷因慢波到达而没有完整地形成。特别指出的是，模拟中的材料均为线弹性，如果计及塑性和黏弹性时仍能出现强烈的加卸载循环的话，则对能量耗散十分有利。

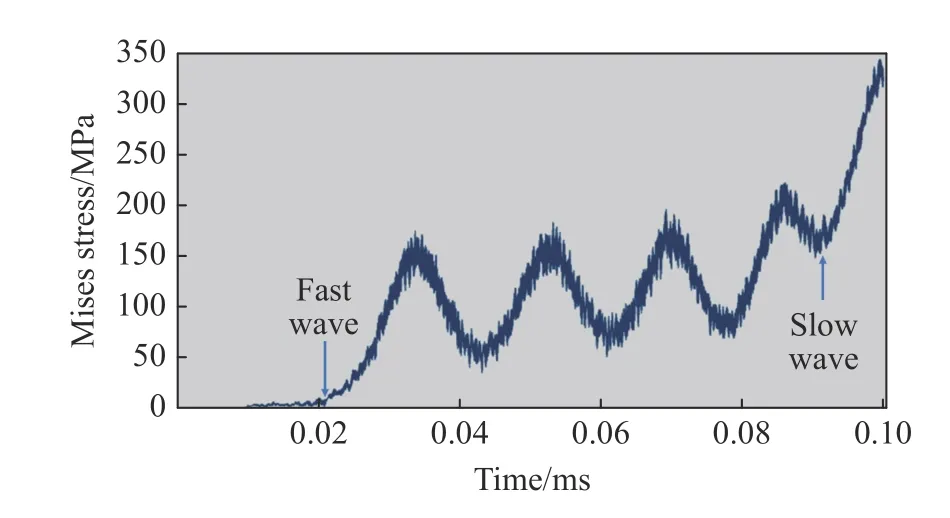
图3 节点P 的Mises 应力随时间的变化曲线Fig. 3 Time history of the Mises stress at nodal point P

2.2 加载速度和摩擦系数对双波波速的影响

本节给出模拟得到的双波波速随加载速度和摩擦系数的变化规律，并结合等效模量的概念和式（3）进行定性讨论。

考虑到在波传播过程中复合纱线严重变形，在包缠纱中取若干节点，将包缠纱主导的沿纵向传播的快波波速定义为节点间初始纵向距离与快波到达时间差之比；同理，在芯纱中取若干节点，将芯纱主导的沿纵向传播的慢波波速定义为节点间初始纵向距离与慢波到达时间差之比。

模拟结果显示，尽管线弹性材料的波速与载荷强度无关，且可由模量、密度和泊松比等材料参数直接计算，但是由线弹性材料构成的螺旋拉胀结构的波速对载荷强度和摩擦系数的依赖关系却并不简单。

图4 给出了固定摩擦系数（零摩擦）时快波和慢波波速随加载速度的变化规律。可见，快波波速随加载速度的增加而增加，而慢波波速正好相反（这种规律在其他摩擦系数下同样成立）。图5 给出了固定加载速度（170 m/s）时快波和慢波波速随摩擦系数的变化规律。可见，快波波速随摩擦系数的增加而减小，慢波波速正好相反（这种规律在其他加载速度下同样成立）。

上述变化规律可以统一解释如下。根据2.1 节的讨论，一方面，空心螺旋弹簧的等效模量（由式（4）给出）是包缠纱等效模量的下限，芯纱通过与包缠纱的相互作用，提供了对包缠纱的支撑，使包缠纱的等效模量高于此下限，芯纱对包缠纱的支撑作用越强，包缠纱的等效模量就越大，反之就越小。另一方面，直线芯纱在快波的作用下预先变形为螺旋状，因此空心螺旋弹簧的等效模量也是芯纱等效模量的下限，芯纱螺旋变形横向膨胀的程度越高（即式（4）中的c 值越大），此下限就越低，反之就越高，而芯纱实际的等效模量也随着该下限而相应地减小或增大。

于是可以理解，在图4 中，加载速度越高意味着包缠纱和芯纱的变形及两者之间的相互作用越强，因此包缠纱的等效模量以及由式（3）确定的快波波速就越大；同时，加载速度越高还意味着芯纱的螺旋变形程度越大，因此其等效模量和由式（3）确定的慢波波速也就越小。在图5 中，摩擦系数越大意味着能量耗散越大，包缠纱和芯纱的运动和变形越弱（模拟结果显示的确如此）。这一方面弱化了包缠纱与芯纱之间的相互作用，从而减小了包缠纱的等效模量以及由式（3）确定的快波波速，另一方面又因为芯纱螺旋变形程度降低，而提高了芯纱的等效模量以及由式（3）确定的慢波波速。另外，在图4 中，快波还使芯纱预先伸长，加载速度越高意味着芯纱预先伸长越多，因此慢波传播经历的路径和所需的时间就越长，根据本节开头关于波速的定义，这也在一定程度上减小了慢波波速。

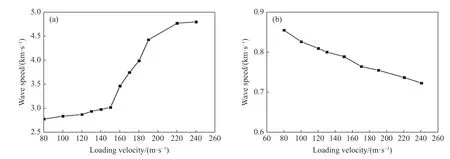
图4 不同加载速度下的快波（a）和慢波（b）波速Fig. 4 Speeds of fast wave (a) and slow wave (b) at different loading velocities

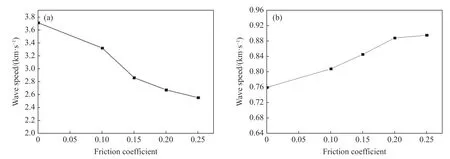
图5 不同摩擦系数下的快波（a）和慢波（b）波速Fig. 5 Speeds of fast wave (a) and slow wave (b) at different friction coefficients

2.3 内能与动能的分配及摩擦耗能

在爆炸与冲击防护应用中，材料和结构快速扩散和吸收局部冲击能量的能力至关重要。鉴于此，初步研究了在恒定速度边界、持续做功的条件下，螺旋拉胀纱线的总动能、内能和摩擦耗能随时间的变化。图6 显示了加载速度为190 m/s、摩擦系数为0.2 时的典型模拟结果。可见，动能随时间略微偏离线性增长，内能随时间基本线性增长，但两者总是基本相等。这是一个比较特别的结果，说明尽管螺旋拉胀纱线中双波引起的运动和变形严重偏离一维平面应变条件，但其能量分配仍符合冲击波理论关于一维平面应变冲击波后内能与动能基本相等的结论。由于所模拟的芯纱和包缠纱均为线弹性材料且不断裂，因此摩擦是能量耗散的唯一机制。从图6 可以看到，起初摩擦耗能的占比很低，但随着时间的推进，逐渐变得重要，这是由于芯纱和包缠纱之间的摩擦主要发生于周期性横向膨胀-收缩区域，而该区域的长度随着时间的推进而增加。

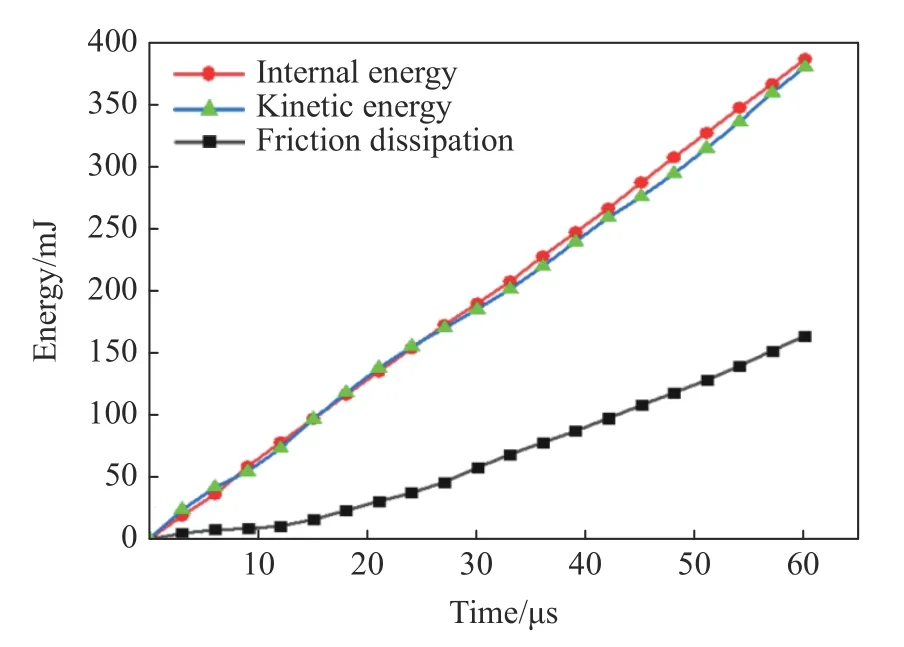
图6 典型算例中的内能、动能及摩擦耗能的时间历史曲线Fig. 6 Time histories of internal energy, kinetic energy and friction dissipation for a typical simulation

3 结 论

基于有限元模拟，开展了螺旋拉胀纱线的冲击动力学行为研究，得到如下主要结果。

（1）在纵向动态拉伸作用下，在螺旋拉胀纱线中存在着分别由包缠纱和芯纱所主导的一快一慢两个应力波，并且两个波阵面之间的区域呈现出一种新奇的应力波现象：由原本直线的芯纱变形成为的螺旋环，每几个一组，沿横向随时间和空间周期性地膨胀-收缩变化，应力加卸载循环十分显著。该现象的物理本质尚不清楚。

（2）加载速度和摩擦系数对双波波速具有显著的影响。快波波速随加载速度的增加而增加，随摩擦系数的增加而减小，慢波的情况正好相反。借助等效模量的概念可以对此进行定性解释。

（3）尽管螺旋拉胀纱线中双波引起的运动和变形严重偏离一维平面应变条件，但其能量的分配仍符合冲击波理论关于一维平面应变冲击波后内能与动能基本相等的结论。摩擦对能量吸收有重要贡献。

上述结果初步涉及了螺旋拉胀纱线的抗冲击机理，可为进一步开展相关实验和理论研究提供依据，并为螺旋拉胀纱线在爆炸与冲击防护领域中的应用提供一定的参考。