水下多点爆炸条件下的冲击波载荷特性

余 俊，盛振新，毛海斌，王海坤

（中国船舶科学研究中心，江苏 无锡 214082）

在岛礁登陆、介入与反介入等典型作战任务和场景下，武器装备与人员遭受的威胁比常规作战更复杂，除了会遭受单枚武器攻击外，还可能遭受多枚武器的攻击。因此，多点爆炸特性研究对于人员和装备的防护技术进步具有重要的参考价值。目前对于多点爆炸情形，已有学者开展了相关研究。李旭东[1]、张世豪等[2]分别采用LS-DYNA 和AUTODYN 两种软件对混凝土中的多点爆炸问题开展了数值模拟，分析了混凝土类介质中冲击波相互作用规律，发现在同等药量条件下，采用多点爆炸可以提高装药的毁伤能力。陈明生等[3]利用LS-DYNA 对4 个非圆柱体云雾爆炸超压的相互作用过程进行了数值模拟，在中心区域地面依次出现三重冲击波现象。翟红波等[4]开展了某舰船舱室1∶8 等效缩比模型内的双点装药同步起爆试验，并与单点起爆进行了对比分析，发现双点起爆的冲击波在装药中心面上相互叠加，冲击波冲量效应比同等药量的单点爆炸显著增加，有效提高了毁伤能力。孟闻远等[5]利用DYNA 开展了两点水下爆炸冲击波对冰体的破坏效应，发现起爆间距对冲击波的毁伤能力影响较大。总体上看，目前大部分研究是基于商业软件进行计算，计算精度难以掌握，计算的可扩展性受到一定限制。其次，对于多爆源起爆问题，爆炸冲击波载荷对于毁伤评估具有重要的参考价值，目前的商业软件对冲击波载荷的计算精度不高，影响了武器毁伤效应的精确评估。针对上述研究存在的不足，本工作针对水下多点爆炸工况开展研究。目前对于水下单爆源的爆炸载荷研究较为成熟，无论是理论研究还是数值模拟，都取得了大量的研究成果[6-9]。然而，对于水下多点爆炸条件下的载荷特征，目前的研究成果不多，在有关多点起爆条件下冲击波相互作用的规律认识等方面还存在很大的不足[10]。而实战中水下多点起爆发生的概率非常大，因此迫切需要对该问题开展相应的研究工作。

本研究采用自研的高精度多相可压缩流体计算程序，模拟水下多爆源爆炸过程中早期冲击波的传播以及冲击波之间的相互作用过程，以获得典型位置处的流体载荷特征，并对流场载荷特性进行初步的归纳总结。

1 载荷计算模型

1.1 理论模型

对于水下爆炸过程中伴随冲击波传播与气泡相互作用过程的多相流运动，采用多相可压缩流体的Five-equation 模型来进行数值模拟。该模型是在无黏可压缩欧拉流体控制方程的基础上引入流体体积分数以及流体输运方程，二维轴对称模型的控制方程为[11-12]

式中：u、v 分别代表流场中x、r 方向的速度分量， ρ1、 ρ2分别为第1 相和第2 相的密度， z1、 z2分别为第1 相和第2 相的体积分数，E 为单位体积总能量，p 为混合压力。对于两相均采用刚性状态方程的流体 ，其单相流体状态方程为[13]

式 中： e 为单位质量内能， ρ为流体密度， γ、p∞为介质的拟合参数。

1.2 离散方法

控制方程采用有限体积法进行空间离散，流场的计算采用TVD 格式[14]，对于空间离散

式中： Δxi、Δrj分别为单元 ( i,j) 沿 x、r 方向的空间步长，为 单元物理量的体积平均值，分 别为 x、r方向的数值通量，即

1.3 计算步骤

求解两相可压缩流体界面运动的主要步骤如下：

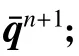
（5）回到步骤（1），开始下一时刻的计算，直至计算结束。

2 计算模型的考核验证

本研究基于水下爆炸早期冲击波的传播及其相互作用过程进行分析，为了对上述计算方法与数值模型进行考核验证，拟采取水下自由场条件下爆炸的早期冲击波压力及其冲量结果作为模拟对象，与Cole 的理论经验公式进行对比。这里计算模型为二维轴对称模型，采用均匀结构网格，网格尺寸取药包半径的1/10 左右。计算域取最大爆炸气泡半径的5 倍以上，边界条件设置为无反射边界。TNT 装药采用瞬时爆轰模型[18]，认为炸药爆轰瞬时形成一团高温、高压的均匀爆轰产物，爆轰产物的密度与未爆炸药相同。TNT 装药的初始化学能约为4.4 MJ，采用理想气体状态方程、比热常数为1.5 时，对应的初始压力约为3.586 GPa，CFL 取0.6。则TNT 爆炸气体初始状态参数可设置为

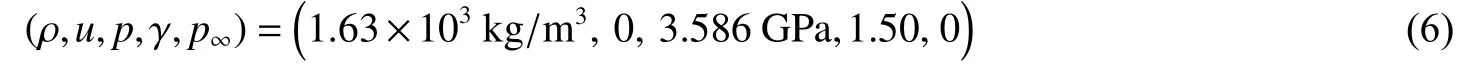
模拟的水深约为水下100 m。由于模拟的是初始冲击波压力的传播，忽略水的初始静水压力与密度的梯度分布，将水设置成均匀密度场（密度均为103kg/m3）与压力场（静水压约为106Pa），同时忽略水的初始密度分布梯度。采用刚性状态方程模拟[11]，水的初始状态参数可设置为

选择0.1 和1.0 kg 的TNT 装药在自由场水下爆炸工况，采用与药包中心的距离为6 倍和12 倍药包半径（R0）处的压力作为校核标的，如图1、图2 所示，其中冲量时程曲线是通过对压力曲线积分得到的。

图1 0.1 kg TNT 装药两测点处压力和冲量时程曲线比较Fig. 1 Comparison of pressure and impulse time history curves at two measuring points of 0.1 kg TNT charge

图2 1.0 kg TNT 装药两测点处压力和冲量时程曲线比较Fig. 2 Comparison of pressure and impulse time history curves at two measuring points of 1.0 kg TNT charge

将上述4 种工况下的自由场冲击波载荷峰值的数值模拟结果和Cole 的经验公式计算结果进行对比[6-7]，如表1 所示。由表1 可知，数值模拟的峰值压力与经验公式计算值的相对偏差基本控制在6%以内。对于冲量，6R0测点处的估算值与经验公式计算值较为一致，而12R0处两者在冲击波早期吻合较好，冲击波中后期存在一定误差。从冲击波峰值和冲量的整体评估上来看，误差在可接受范围以内，说明本计算模型可以用于水下爆炸冲击波阶段的数值模拟。

表1 计算结果与由Cole 经验公式得到的峰值压力对比Table 1 Comparison of peak pressure between calculated results and Cole empirical formula

3 水下多点爆炸的计算与分析

3.1 计算工况简介

图3 双爆源测点分布Fig. 3 Location of measuring points of double explosion sources

计算工况为1.0 kg TNT 水下100 m 爆炸，药包半径R0=0.052 7 m。计算域长8 m，宽6 m，采用二维轴对称模型计算，计算域大小、边界条件设置、网格大小等选取方法同第2 节。两爆源的距离D=12R0=0.63 m。

计算域及测点分布如图3 所示：A1～A4测点爆距分别为6R0、8R0、12R0、20R0。B1、B2位于左侧爆源S1 正上方，与S1 的距离分别为6R0和12R0。C1、C2位于爆源S1 的左侧，与S1 的横向距离分别为6R0、16R0，纵向距离分别为8R0、14R0。将单点爆炸作为对比工况，测点布局与图3 相同，只是去掉爆源S2。

3.2 流场压力与密度的典型演化过程

单爆源和双爆源这两种不同工况下流场典型时刻的演化过程如图4 所示。

图4 单爆源(a)和双爆源(b)工况下流场的演化过程（上：压力云图，下：密度云图）Fig. 4 Evolution of flow field under the conditions of double explosion sources (a) and single explosion source (b) (Up：pressure cloud image, down：density cloud image)

由图4 可知，双爆源同时起爆后，两个冲击波在初始碰撞后继续沿各自路径传播，在两个爆源的对称面上出现压力“热点”，该局部“热点”会随着波阵面一起移动。其中一个爆源的冲击波阵面经过另一个爆源的爆炸气体后，对冲击波产生明显的衰减作用，这些现象是单爆源工况中没有的。

3.3 对称面上测点A1～A4 的载荷比较

测点A1～A4是两爆源对称面上的典型测点，测点与爆源的距离在6R0～20R0之间。将双爆源和单爆源两种工况下4 个测点的压力时程曲线进行对比，其中A1～A4为双爆源工况下直接计算得到的该测点处的压力曲线，A11～A44为爆源S1、S2 独立存在时在A1～A4的压力的直接线性叠加（以下称为两个单爆源线性叠加工况），如图5 所示，后续的压力曲线中B11、B22、C11、C22也依此定义。表2 列出了测点A1～A4在两种工况下的峰值压力对比。

图5 测点A1～A4 的压力时程曲线对比Fig. 5 Comparison of pressure time history curves at points A1-A4

表2 峰值压力比较Table 2 Comparison of peak pressures

由表2 可知，在6R0～20R0范围内，双爆源的峰值压力相比两个单爆源线性叠加的峰值压力有不同程度的增加，增加幅度在12%～16%之间。因此，在实际评估双爆源对称面上测点压力时，无论是采用单爆源工况下的理论经验公式，还是数值模拟结果，直接采用线性叠加方式计算双爆源工况下的载荷都存在较大的误差，难以满足计算精度要求。

3.4 测点B1～B2 的载荷比较

测点B1和B2在双爆源工况与两个单爆源线性叠加工况下的压力载荷曲线对比如图6 所示。可见，2 个测点均存在“双峰”现象。其中第1 个压力峰值对于两种工况完全吻合，而对于第2 个波峰，双爆源工况下的峰值比两个单爆源线性叠加的峰值稍小，峰值下降幅度在5%以内。这是由于第1 个峰值是近端爆源S1 的冲击波传播过来的，而第2 个峰值是爆源S2 传播过来的，S2 的冲击波传播到测点B1、B2之前已经与爆源S1 产生的爆炸气团作用。早期冲击波速度在1 800 m/s 左右，气泡膨胀的平均速度在200 m/s 左右。在爆源S2 的冲击波阵面到达测点B1之前，已经在爆源S1 的爆炸气团表面反射稀疏波（如图6 中右图所示），从而对测点B1、B2的压力产生一定的衰减作用。

图6 测点B1 和B2 的压力曲线对比Fig. 6 Comparison of pressure curves at points B1 and B2

3.5 测 点C1～C2 的 载 荷 比 较

测点C1、C2在双爆源以及两个单爆源线性叠加工况下的压力载荷曲线对比如图7 所示。由于两个爆源的冲击波到达C1或C2存在时间差，因此双爆源和两个单爆源线性叠加的第一个波峰完全一致。对于第2 个波峰，由于爆源S2 的冲击波先作用于气泡后，反射的稀疏波和直达波几乎同时到达该测点，因此无论是峰值还是衰减速度，双爆源工况都较两个单爆源线性叠加工况有很大程度的衰减，峰值下降幅度约为30%，其原理与3.4 节类似，不再赘述。

图7 测点C1 和C2 的压力曲线比较Fig. 7 Comparison of pressure curves at points C1 and C2

4 总结与展望

针对舰艇结构可能遭受水下多点攻击的实战情形，开展了水下两点同时起爆条件下水下爆炸载荷特征的数值模拟研究。基于多相可压缩理论模型及其离散方法，采用高精度的数值格式求解数值模型，并对数值模型进行了初步的试验验证以及与理论计算结果比较，证明了数值模型计算的可靠性。在此基础上计算了典型工况下水下两点起爆模型，通过对部分区域测点的压力比较，得到以下结论：

（1）两点起爆时，在爆源的对称面上，由于冲击波载荷同时到达，存在冲击波之间的碰撞效应，因此对称面上的峰值压力相比两个单爆源线性叠加时有不同程度的增加，增加幅度在12%～16%之间；

（2）对于两爆源垂直截面之间且处于非对称面上的测点，由于两个爆源的冲击波到达存在时间差，因此压力时程曲线表现为双峰现象，其中第1 个峰值压力与两个单爆源线性叠加时的峰值压力相等，第2 个峰值压力要稍低于两个单爆源线性叠加时的峰值压力，下降幅度在5%以内；

（3）对于两爆源垂直截面之外的测点，压力同样存在双峰现象，第1 个峰值压力与两个单爆源线性叠加时的峰值压力相等，第2 个峰值压力则远低于两个单爆源线性叠加时的峰值压力，下降幅度可达30%左右。

上述获得的初步结论针对的是部分典型工况，要想获得多点爆炸载荷的规律，仍然需要大量工况的对比分析，除了要考虑多爆源同时起爆外，还需要考虑延时起爆，以及不同数量爆源的起爆等情形，这些有望在后续研究中开展。